2022-2023学年陕西省西安市长安区九年级(下)期中数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年陕西省西安市长安区九年级(下)期中数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 600.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 16:42:51 | ||
图片预览



文档简介
2022-2023学年陕西省西安市长安区九年级(下)期中数学试卷
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.(4分)﹣2的倒数是( )
A.2 B.﹣2 C. D.﹣
2.(4分)如图是由5个大小相同的正方体摆成的立方体图形,它的左视图是( )
A. B. C. D.
3.(4分)2012年3月5日上午,国务院总理温家宝向第十一届全国人大五次会议作政府工作报告时提出,2012年中央财政要进一步增加教育投入,国家财政性教育经费支出21984.63亿元.将21984.63用科学记数法可表示为( )
A.21.98463×103 B.0.2198463×105
C.2.198463×104 D.2.198463×103
4.(4分)如图.已知AB∥CD,∠1=70°,则∠2的度数是( )
A.60° B.70° C.80° D.110
5.(4分)下列运算正确的是( )
A.2﹣2=﹣4 B.(a2)3=a5
C.2x3+3x3=5x3 D.x8÷x4=x2
6.(4分)方程组的解是( )
A. B. C. D.
7.(4分)某校篮球班21名同学的身高如下表
身高cm 180 186 188 192 208
人数(个) 4 6 5 4 2
则该校篮球班21名同学身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.186,188 D.208,188
8.(4分)如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=(x+3)2 B.y=(x+3)2
C.y=(x﹣3)2 D.y=(x﹣3)2
9.(4分)函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:
①两函数图象的交点坐标为A(2,2);
②当x>2时,y2>y1;
③直线x=1分别与两函数图象交于B、C两点,则线段BC的长为3;
④当x逐渐增大时,y1的值随着x的增大而增大,y2的值随着x的增大而减小.
则其中正确的是( )
A.只有①② B.只有①③ C.只有②④ D.只有①③④
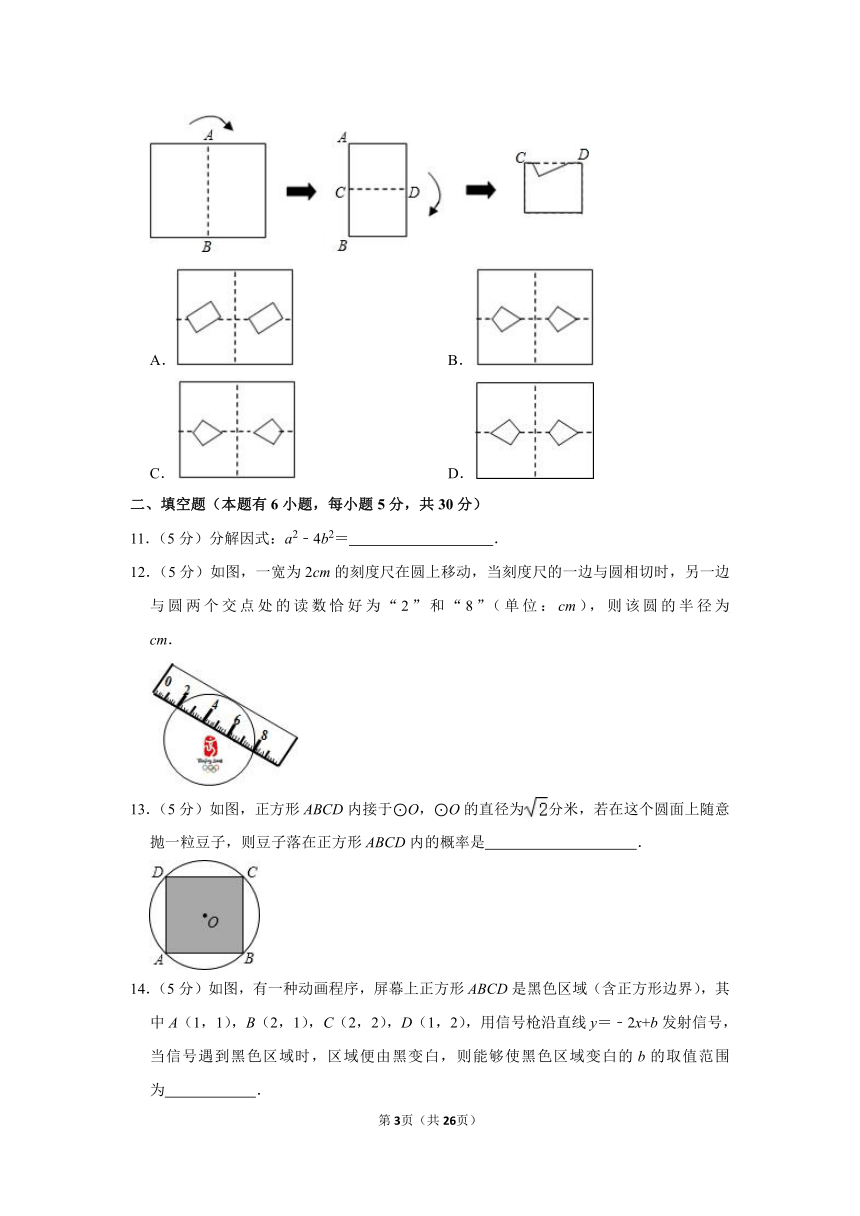
10.(4分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
二、填空题(本题有6小题,每小题5分,共30分)
11.(5分)分解因式:a2﹣4b2= .
12.(5分)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm.
13.(5分)如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是 .
14.(5分)如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=﹣2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为 .
15.(5分)定义运算a b=a(1﹣b),下列给出了关于这种运算的几个结论:
①2 (﹣2)=6;
②a b=b a;
③若a+b=0,则(a a)+(b b)=2ab;
④若a b=0,则a=0.
其中正确结论的序号是 .(在横线上填上你认为所有正确结论的序号)
16.(5分)如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点An的坐标为 .
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80
17.(8分)计算:()﹣1+(﹣2009)0﹣+2sin30°.
18.(8分)解方程:=.
19.(8分)现有如图1所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案(如示例图2):
(1)在图3拼铺的图案成轴对称图形;
(2)在图4拼铺的图案成中心对称图形;
(3)在图5拼铺的图案既是轴对称图形,又是中心对称图形.
(要求:三个图各不相同.)
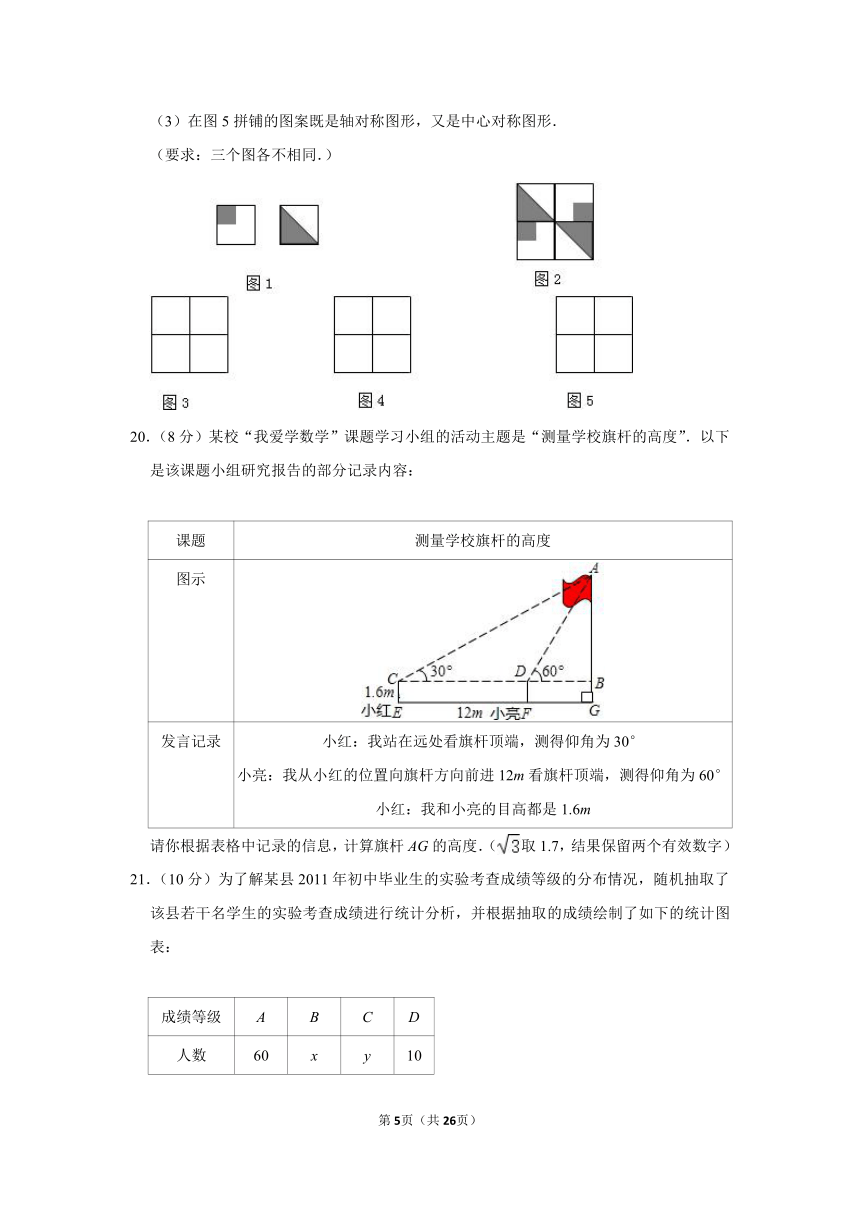
20.(8分)某校“我爱学数学”课题学习小组的活动主题是“测量学校旗杆的高度”.以下是该课题小组研究报告的部分记录内容:
课题 测量学校旗杆的高度
图示
发言记录 小红:我站在远处看旗杆顶端,测得仰角为30°小亮:我从小红的位置向旗杆方向前进12m看旗杆顶端,测得仰角为60°小红:我和小亮的目高都是1.6m
请你根据表格中记录的信息,计算旗杆AG的高度.(取1.7,结果保留两个有效数字)
21.(10分)为了解某县2011年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 A B C D
人数 60 x y 10
百分比 30% 50% 15% m
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有 名;
(2)表中x,y和m所表示的数分别为:x= ,y= ,m= ;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.
22.(12分)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润 B型利润
甲店 200 170
乙店 160 150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
23.(12分)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题探究:
(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:
(2)若将原题中的“正方形”改为“矩形”(如图4所示),且=k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.
拓展应用:
(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
24.(14分)如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部分)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积,
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
2022-2023学年陕西省西安市长安区九年级(下)期中数学试卷
参考答案与试题解析
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.(4分)﹣2的倒数是( )
A.2 B.﹣2 C. D.﹣
【解答】解:∵﹣2×()=1,
∴﹣2的倒数是﹣.
故选:D.
2.(4分)如图是由5个大小相同的正方体摆成的立方体图形,它的左视图是( )
A. B. C. D.
【解答】解:从左往右看,得到从左往右2列正方形的个数依次为2,1,
故选:C.
3.(4分)2012年3月5日上午,国务院总理温家宝向第十一届全国人大五次会议作政府工作报告时提出,2012年中央财政要进一步增加教育投入,国家财政性教育经费支出21984.63亿元.将21984.63用科学记数法可表示为( )
A.21.98463×103 B.0.2198463×105
C.2.198463×104 D.2.198463×103
【解答】解:将21984.63用科学记数法表示为2.198463×104.
故选:C.
4.(4分)如图.已知AB∥CD,∠1=70°,则∠2的度数是( )
A.60° B.70° C.80° D.110
【解答】解:∵AB∥CD,
∴∠1=∠3=70°,
∵∠2+∠3=180°,
∴∠2=110°.
故选:D.
5.(4分)下列运算正确的是( )
A.2﹣2=﹣4 B.(a2)3=a5
C.2x3+3x3=5x3 D.x8÷x4=x2
【解答】解:A、2﹣2=;
B、(a2)3=a6;
C、正确;
D、x8÷x4=x4.
故选:C.
6.(4分)方程组的解是( )
A. B. C. D.
【解答】解:,
(1)+(2)得,
3x=6,
x=2,
把x=2代入(1)得,y=﹣1,
∴原方程组的解.
故选:D.
7.(4分)某校篮球班21名同学的身高如下表
身高cm 180 186 188 192 208
人数(个) 4 6 5 4 2
则该校篮球班21名同学身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.186,188 D.208,188
【解答】解:众数是:186cm;
中位数是:188cm.
故选:C.
8.(4分)如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=(x+3)2 B.y=(x+3)2
C.y=(x﹣3)2 D.y=(x﹣3)2
【解答】解:∵高CH=1cm,BD=2cm,
而B、D关于y轴对称,
∴D点坐标为(1,1),
∵AB∥x轴,AB=4cm,最低点C在x轴上,
∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(﹣3,0),
∴右边抛物线的顶点C的坐标为(3,0),
设右边抛物线的解析式为y=a(x﹣3)2,
把D(1,1)代入得1=a×(1﹣3)2,解得a=,
故右边抛物线的解析式为y=(x﹣3)2.
故选:C.
9.(4分)函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:
①两函数图象的交点坐标为A(2,2);
②当x>2时,y2>y1;
③直线x=1分别与两函数图象交于B、C两点,则线段BC的长为3;
④当x逐渐增大时,y1的值随着x的增大而增大,y2的值随着x的增大而减小.
则其中正确的是( )
A.只有①② B.只有①③ C.只有②④ D.只有①③④
【解答】解:①函数y1=x(x≥0),y2=(x>0)组成方程组,
解之得,即两函数图象的交点坐标为A(2,2),故①正确;
②由图象直接可得当x>2时,y2<y1,故②错误;
③把x=1分别代入函数y1=x(x≥0),y2=(x>0),可得y1=1,y2=4,
∴BC的长为3,故③正确;
④函数y1=x(x≥0)中,k>0,y随x增大而增大,
y2=(x>0)中,k>0,在每一象限内y随x增大而减小,故④正确.
故选:D.
10.(4分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
【解答】解:∵第三个图形是三角形,
∴将第三个图形展开,可得,即可排除答案A,
∵再展开可知两个短边正对着,
∴选择答案D,排除B与C.
故选:D.
二、填空题(本题有6小题,每小题5分,共30分)
11.(5分)分解因式:a2﹣4b2= (a+2b)(a﹣2b) .
【解答】解:a2﹣4b2=(a+2b)(a﹣2b).
故答案为:(a+2b)(a﹣2b).
12.(5分)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm.
【解答】解:作OE垂直AB于E,交⊙O于D,
设OB=r,
根据垂径定理,BE=AB=×6=3cm,
根据题意列方程得:(r﹣2)2+9=r2,解得r=,
∴该圆的半径为cm.
13.(5分)如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是 .
【解答】解:因为⊙O的直径为分米,则半径为分米,⊙O的面积为π()2=平方分米;
正方形的边长为=1分米,面积为1平方分米;
因为豆子落在圆内每一个地方是均等的,
所以P(豆子落在正方形ABCD内)==.
故答案为:.
14.(5分)如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=﹣2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为 3≤b≤6 .
【解答】解:由题意可知当直线y=﹣2x+b经过A(1,1)时b的值最小,即﹣2×1+b=1,b=3;
当直线y=﹣2x+b过C(2,2)时,b最大即2=﹣2×2+b,b=6,故能够使黑色区域变白的b的取值范围为3≤b≤6.
15.(5分)定义运算a b=a(1﹣b),下列给出了关于这种运算的几个结论:
①2 (﹣2)=6;
②a b=b a;
③若a+b=0,则(a a)+(b b)=2ab;
④若a b=0,则a=0.
其中正确结论的序号是 ①③ .(在横线上填上你认为所有正确结论的序号)
【解答】解:∵a b=a(1﹣b),
①2 (﹣2)=6
=2×[1﹣(﹣2)]
=2×3
=6
故本选项正确;
②a b
=a×(1﹣b)
=a﹣ab
b a
=b(1﹣a)
=b﹣ab,
故本选项错误;
③∵(a a)+(b b)
=[a(1﹣a)]+[b(1﹣b)]
=a﹣a2+b﹣b2,
∵a+b=0,
∴原式=(a+b)﹣(a2+b2)
=0﹣[(a+b)2﹣2ab]
=2ab,
故本选项正确;
④∵a b
=a(1﹣b)=0,
∴a=0错误.
故答案为:①③
16.(5分)如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点An的坐标为 () .
【解答】解:∵点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点,
∴A1的纵坐标为1,横坐标为:=,即A1(,1);
同理可求:A2(,2),A3(,3)
∴根据这些具体值,得出规律:An的纵坐标是n,横坐标是.即An的坐标为().
故答案为:().
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80
17.(8分)计算:()﹣1+(﹣2009)0﹣+2sin30°.
【解答】解:原式=2+1﹣3+2×=1.
18.(8分)解方程:=.
【解答】解:方程的两边同乘x(x﹣1),得
3x﹣3=2x,
解得x=3.
检验:把x=3代入x(x﹣1)=6≠0.
∴原方程的解为:x=3.
19.(8分)现有如图1所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案(如示例图2):
(1)在图3拼铺的图案成轴对称图形;
(2)在图4拼铺的图案成中心对称图形;
(3)在图5拼铺的图案既是轴对称图形,又是中心对称图形.
(要求:三个图各不相同.)
【解答】解:(1)所作图形如下:
;
(2)所作图形如下:
;
(3)所作图形如下:
.
20.(8分)某校“我爱学数学”课题学习小组的活动主题是“测量学校旗杆的高度”.以下是该课题小组研究报告的部分记录内容:
课题 测量学校旗杆的高度
图示
发言记录 小红:我站在远处看旗杆顶端,测得仰角为30°小亮:我从小红的位置向旗杆方向前进12m看旗杆顶端,测得仰角为60°小红:我和小亮的目高都是1.6m
请你根据表格中记录的信息,计算旗杆AG的高度.(取1.7,结果保留两个有效数字)
【解答】解:解法一:设BD=xm,AB=xm,
在Rt△ABC中,tan30°=,即= …(4分)
解得x=6,
∴AB=6 …(6分)
∴AG=6+1.6≈6×1.7+1.6≈12m …(8分)
解法二:∵∠ACB=30°,∠ADB=60°,
∴∠CAD=60°﹣∠ACB=30°=∠ACB,
∴AD=CD=12 …(2分)
在Rt△ADB中,sin60°=,即= …(4分)
∴AB=6 …(6分)
∴AG=6+1.6≈6×1.7+1.6≈12m …(8分)
21.(10分)为了解某县2011年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 A B C D
人数 60 x y 10
百分比 30% 50% 15% m
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有 200 名;
(2)表中x,y和m所表示的数分别为:x= 100 ,y= 30 ,m= 5% ;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.
【解答】解:(1)60÷30%=200名;
(2)x=200×50%=100,y=200×15%=30,m=1﹣95%=5%;
(3)
(4)5400×5%=270名.
答:估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数为270名.
22.(12分)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润 B型利润
甲店 200 170
乙店 160 150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
【解答】解:依题意,分配给甲店A型产品x件,则甲店B型产品有(70﹣x)件,乙店A型有(40﹣x)件,B型有{30﹣(40﹣x)}件,则
(1)W=200x+170(70﹣x)+160(40﹣x)+150(x﹣10)=20x+16800.
由,解得10≤x≤40.
(2)由W=20x+16800≥17560,
∴x≥38.
∴38≤x≤40,x=38,39,40.
∴有三种不同的分配方案.
方案一:x=38时,甲店A型38件,B型32件,乙店A型2件,B型28件;
方案二:x=39时,甲店A型39件,B型31件,乙店A型1件,B型29件;
方案三:x=40时,甲店A型40件,B型30件,乙店A型0件,B型30件.
(3)依题意:200﹣a>170,即a<30,
W=(200﹣a)x+170(70﹣x)+160(40﹣x)+150(x﹣10)=(20﹣a)x+16800,(10≤x≤40).
①当0<a<20时,20﹣a>0,W随x增大而增大,
∴x=40,W有最大值,
即甲店A型40件,B型30件,乙店A型0件,B型30件,能使总利润达到最大;
②当a=20时,10≤x≤40,W=16800,符合题意的各种方案,使总利润都一样;
③当20<a<30时,20﹣a<0,W随x增大而减小,
∴x=10,W有最大值,
即甲店A型10件,B型60件,乙店A型30件,B型0件,能使总利润达到最大.
23.(12分)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题探究:
(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:
(2)若将原题中的“正方形”改为“矩形”(如图4所示),且=k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.
拓展应用:
(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
【解答】解;(1)①BG=DE,BG⊥DE;
②仍然成立,选择图2证明如下:
证明:∵四边形ABCD、CEFG都是正方形;
∴BC=CD,CG=CE,∠BCD=∠ECG,
∴∠BCG=∠DCE,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE;
(2)BG⊥DE,=k,
如图5,
证明:
∵四边形ABCD,CEFG都是矩形,且==k,
∴==k,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
∴△BCG∽△DCE,
∴∠CBG=∠CDE,=k,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE;
(3)∵BG⊥DE,
∴BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2,
又∵AB=3,CE=2,
∴BD=3,GE=2,
∴BD2+GE2=(3)2+(2)2=26,
∴BE2+DG2=26.
24.(14分)如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部分)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积,
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
【解答】解:(1)①AB=2
OA==4,OC=4,S梯形OABC=12
②当2<t<4时,
直角梯形OABC被直线l扫过的面积=直角梯形OABC面积一直角三角形DOE面积,
∵AB∥CD,OA=4,
∴==,
∴OE=8﹣2t
S=12﹣(4﹣t)×(8﹣2t)=﹣t2+8t﹣4;
(2)存在
P1(﹣12,4),P2(﹣4,4),P3(﹣,4),P4(4,4),P5(8,4)
下面提供参考解法二:
以直角进行分类进行讨论(分三类):
第一类如上分析中①所示图∠P为直角:
设直线DE:y=2x+2b,此时D(﹣b,0),E(0,2b)的中点坐标为,
直线DE的中垂线方程:y﹣b=﹣,
令y=4得.
由已知可得PE=DE即
化简得3b2﹣32b+64=0
解得b1=8,b2=将之代入P(﹣8,4)
∴P1=(4,4)P2(﹣4,4);
第二类如上分析中②所示图∠E为直角:
设直线DE:y=2x+2b,此时D(﹣b,o),E(O,2b),
直线PE的方程:y=﹣,
令y=4得P(4b﹣8,4).
由已知可得PE=DE即
化简得b2=(2b﹣8)2
解之得,b1=4,b2=将之代入P(4b﹣8,4)
∴P3=(8,4)
第三类如上分析中③所示图∠D为直角:
设直线DE:y=2x+2b,此时D(﹣b,o),E(O,2b),
直线PD的方程:y=﹣(x+b),
令y=4得P(﹣b﹣8,4).
由已知可得PD=DE即
解得b1=4,b2=﹣4将之代入P(﹣b﹣8,4)
∴P5=(﹣12,4)、P6(﹣4,4)、[P6(﹣4,4)与P2重合舍去].
综上可得P点的坐标共5个解,分别为P(﹣12,4)、P(﹣4,4)、P(﹣,4)、
P(8,4)、P(4,4).
事实上,我们可以得到更一般的结论:
如果得出AB=a、OC=b、OA=h、设,则P点的情形如下:
第1页(共1页)
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.(4分)﹣2的倒数是( )
A.2 B.﹣2 C. D.﹣
2.(4分)如图是由5个大小相同的正方体摆成的立方体图形,它的左视图是( )
A. B. C. D.
3.(4分)2012年3月5日上午,国务院总理温家宝向第十一届全国人大五次会议作政府工作报告时提出,2012年中央财政要进一步增加教育投入,国家财政性教育经费支出21984.63亿元.将21984.63用科学记数法可表示为( )
A.21.98463×103 B.0.2198463×105
C.2.198463×104 D.2.198463×103
4.(4分)如图.已知AB∥CD,∠1=70°,则∠2的度数是( )
A.60° B.70° C.80° D.110
5.(4分)下列运算正确的是( )
A.2﹣2=﹣4 B.(a2)3=a5
C.2x3+3x3=5x3 D.x8÷x4=x2
6.(4分)方程组的解是( )
A. B. C. D.
7.(4分)某校篮球班21名同学的身高如下表
身高cm 180 186 188 192 208
人数(个) 4 6 5 4 2
则该校篮球班21名同学身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.186,188 D.208,188
8.(4分)如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=(x+3)2 B.y=(x+3)2
C.y=(x﹣3)2 D.y=(x﹣3)2
9.(4分)函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:
①两函数图象的交点坐标为A(2,2);
②当x>2时,y2>y1;
③直线x=1分别与两函数图象交于B、C两点,则线段BC的长为3;
④当x逐渐增大时,y1的值随着x的增大而增大,y2的值随着x的增大而减小.
则其中正确的是( )
A.只有①② B.只有①③ C.只有②④ D.只有①③④
10.(4分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
二、填空题(本题有6小题,每小题5分,共30分)
11.(5分)分解因式:a2﹣4b2= .
12.(5分)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm.
13.(5分)如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是 .
14.(5分)如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=﹣2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为 .
15.(5分)定义运算a b=a(1﹣b),下列给出了关于这种运算的几个结论:
①2 (﹣2)=6;
②a b=b a;
③若a+b=0,则(a a)+(b b)=2ab;
④若a b=0,则a=0.
其中正确结论的序号是 .(在横线上填上你认为所有正确结论的序号)
16.(5分)如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点An的坐标为 .
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80
17.(8分)计算:()﹣1+(﹣2009)0﹣+2sin30°.
18.(8分)解方程:=.
19.(8分)现有如图1所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案(如示例图2):
(1)在图3拼铺的图案成轴对称图形;
(2)在图4拼铺的图案成中心对称图形;
(3)在图5拼铺的图案既是轴对称图形,又是中心对称图形.
(要求:三个图各不相同.)
20.(8分)某校“我爱学数学”课题学习小组的活动主题是“测量学校旗杆的高度”.以下是该课题小组研究报告的部分记录内容:
课题 测量学校旗杆的高度
图示
发言记录 小红:我站在远处看旗杆顶端,测得仰角为30°小亮:我从小红的位置向旗杆方向前进12m看旗杆顶端,测得仰角为60°小红:我和小亮的目高都是1.6m
请你根据表格中记录的信息,计算旗杆AG的高度.(取1.7,结果保留两个有效数字)
21.(10分)为了解某县2011年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 A B C D
人数 60 x y 10
百分比 30% 50% 15% m
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有 名;
(2)表中x,y和m所表示的数分别为:x= ,y= ,m= ;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.
22.(12分)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润 B型利润
甲店 200 170
乙店 160 150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
23.(12分)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题探究:
(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:
(2)若将原题中的“正方形”改为“矩形”(如图4所示),且=k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.
拓展应用:
(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
24.(14分)如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部分)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积,
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
2022-2023学年陕西省西安市长安区九年级(下)期中数学试卷
参考答案与试题解析
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1.(4分)﹣2的倒数是( )
A.2 B.﹣2 C. D.﹣
【解答】解:∵﹣2×()=1,
∴﹣2的倒数是﹣.
故选:D.
2.(4分)如图是由5个大小相同的正方体摆成的立方体图形,它的左视图是( )
A. B. C. D.
【解答】解:从左往右看,得到从左往右2列正方形的个数依次为2,1,
故选:C.
3.(4分)2012年3月5日上午,国务院总理温家宝向第十一届全国人大五次会议作政府工作报告时提出,2012年中央财政要进一步增加教育投入,国家财政性教育经费支出21984.63亿元.将21984.63用科学记数法可表示为( )
A.21.98463×103 B.0.2198463×105
C.2.198463×104 D.2.198463×103
【解答】解:将21984.63用科学记数法表示为2.198463×104.
故选:C.
4.(4分)如图.已知AB∥CD,∠1=70°,则∠2的度数是( )
A.60° B.70° C.80° D.110
【解答】解:∵AB∥CD,
∴∠1=∠3=70°,
∵∠2+∠3=180°,
∴∠2=110°.
故选:D.
5.(4分)下列运算正确的是( )
A.2﹣2=﹣4 B.(a2)3=a5
C.2x3+3x3=5x3 D.x8÷x4=x2
【解答】解:A、2﹣2=;
B、(a2)3=a6;
C、正确;
D、x8÷x4=x4.
故选:C.
6.(4分)方程组的解是( )
A. B. C. D.
【解答】解:,
(1)+(2)得,
3x=6,
x=2,
把x=2代入(1)得,y=﹣1,
∴原方程组的解.
故选:D.
7.(4分)某校篮球班21名同学的身高如下表
身高cm 180 186 188 192 208
人数(个) 4 6 5 4 2
则该校篮球班21名同学身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.186,188 D.208,188
【解答】解:众数是:186cm;
中位数是:188cm.
故选:C.
8.(4分)如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=(x+3)2 B.y=(x+3)2
C.y=(x﹣3)2 D.y=(x﹣3)2
【解答】解:∵高CH=1cm,BD=2cm,
而B、D关于y轴对称,
∴D点坐标为(1,1),
∵AB∥x轴,AB=4cm,最低点C在x轴上,
∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(﹣3,0),
∴右边抛物线的顶点C的坐标为(3,0),
设右边抛物线的解析式为y=a(x﹣3)2,
把D(1,1)代入得1=a×(1﹣3)2,解得a=,
故右边抛物线的解析式为y=(x﹣3)2.
故选:C.
9.(4分)函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:
①两函数图象的交点坐标为A(2,2);
②当x>2时,y2>y1;
③直线x=1分别与两函数图象交于B、C两点,则线段BC的长为3;
④当x逐渐增大时,y1的值随着x的增大而增大,y2的值随着x的增大而减小.
则其中正确的是( )
A.只有①② B.只有①③ C.只有②④ D.只有①③④
【解答】解:①函数y1=x(x≥0),y2=(x>0)组成方程组,
解之得,即两函数图象的交点坐标为A(2,2),故①正确;
②由图象直接可得当x>2时,y2<y1,故②错误;
③把x=1分别代入函数y1=x(x≥0),y2=(x>0),可得y1=1,y2=4,
∴BC的长为3,故③正确;
④函数y1=x(x≥0)中,k>0,y随x增大而增大,
y2=(x>0)中,k>0,在每一象限内y随x增大而减小,故④正确.
故选:D.
10.(4分)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A. B.
C. D.
【解答】解:∵第三个图形是三角形,
∴将第三个图形展开,可得,即可排除答案A,
∵再展开可知两个短边正对着,
∴选择答案D,排除B与C.
故选:D.
二、填空题(本题有6小题,每小题5分,共30分)
11.(5分)分解因式:a2﹣4b2= (a+2b)(a﹣2b) .
【解答】解:a2﹣4b2=(a+2b)(a﹣2b).
故答案为:(a+2b)(a﹣2b).
12.(5分)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm.
【解答】解:作OE垂直AB于E,交⊙O于D,
设OB=r,
根据垂径定理,BE=AB=×6=3cm,
根据题意列方程得:(r﹣2)2+9=r2,解得r=,
∴该圆的半径为cm.
13.(5分)如图,正方形ABCD内接于⊙O,⊙O的直径为分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是 .
【解答】解:因为⊙O的直径为分米,则半径为分米,⊙O的面积为π()2=平方分米;
正方形的边长为=1分米,面积为1平方分米;
因为豆子落在圆内每一个地方是均等的,
所以P(豆子落在正方形ABCD内)==.
故答案为:.
14.(5分)如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=﹣2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为 3≤b≤6 .
【解答】解:由题意可知当直线y=﹣2x+b经过A(1,1)时b的值最小,即﹣2×1+b=1,b=3;
当直线y=﹣2x+b过C(2,2)时,b最大即2=﹣2×2+b,b=6,故能够使黑色区域变白的b的取值范围为3≤b≤6.
15.(5分)定义运算a b=a(1﹣b),下列给出了关于这种运算的几个结论:
①2 (﹣2)=6;
②a b=b a;
③若a+b=0,则(a a)+(b b)=2ab;
④若a b=0,则a=0.
其中正确结论的序号是 ①③ .(在横线上填上你认为所有正确结论的序号)
【解答】解:∵a b=a(1﹣b),
①2 (﹣2)=6
=2×[1﹣(﹣2)]
=2×3
=6
故本选项正确;
②a b
=a×(1﹣b)
=a﹣ab
b a
=b(1﹣a)
=b﹣ab,
故本选项错误;
③∵(a a)+(b b)
=[a(1﹣a)]+[b(1﹣b)]
=a﹣a2+b﹣b2,
∵a+b=0,
∴原式=(a+b)﹣(a2+b2)
=0﹣[(a+b)2﹣2ab]
=2ab,
故本选项正确;
④∵a b
=a(1﹣b)=0,
∴a=0错误.
故答案为:①③
16.(5分)如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点An的坐标为 () .
【解答】解:∵点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点,
∴A1的纵坐标为1,横坐标为:=,即A1(,1);
同理可求:A2(,2),A3(,3)
∴根据这些具体值,得出规律:An的纵坐标是n,横坐标是.即An的坐标为().
故答案为:().
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80
17.(8分)计算:()﹣1+(﹣2009)0﹣+2sin30°.
【解答】解:原式=2+1﹣3+2×=1.
18.(8分)解方程:=.
【解答】解:方程的两边同乘x(x﹣1),得
3x﹣3=2x,
解得x=3.
检验:把x=3代入x(x﹣1)=6≠0.
∴原方程的解为:x=3.
19.(8分)现有如图1所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方形地板图案(如示例图2):
(1)在图3拼铺的图案成轴对称图形;
(2)在图4拼铺的图案成中心对称图形;
(3)在图5拼铺的图案既是轴对称图形,又是中心对称图形.
(要求:三个图各不相同.)
【解答】解:(1)所作图形如下:
;
(2)所作图形如下:
;
(3)所作图形如下:
.
20.(8分)某校“我爱学数学”课题学习小组的活动主题是“测量学校旗杆的高度”.以下是该课题小组研究报告的部分记录内容:
课题 测量学校旗杆的高度
图示
发言记录 小红:我站在远处看旗杆顶端,测得仰角为30°小亮:我从小红的位置向旗杆方向前进12m看旗杆顶端,测得仰角为60°小红:我和小亮的目高都是1.6m
请你根据表格中记录的信息,计算旗杆AG的高度.(取1.7,结果保留两个有效数字)
【解答】解:解法一:设BD=xm,AB=xm,
在Rt△ABC中,tan30°=,即= …(4分)
解得x=6,
∴AB=6 …(6分)
∴AG=6+1.6≈6×1.7+1.6≈12m …(8分)
解法二:∵∠ACB=30°,∠ADB=60°,
∴∠CAD=60°﹣∠ACB=30°=∠ACB,
∴AD=CD=12 …(2分)
在Rt△ADB中,sin60°=,即= …(4分)
∴AB=6 …(6分)
∴AG=6+1.6≈6×1.7+1.6≈12m …(8分)
21.(10分)为了解某县2011年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 A B C D
人数 60 x y 10
百分比 30% 50% 15% m
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有 200 名;
(2)表中x,y和m所表示的数分别为:x= 100 ,y= 30 ,m= 5% ;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.
【解答】解:(1)60÷30%=200名;
(2)x=200×50%=100,y=200×15%=30,m=1﹣95%=5%;
(3)
(4)5400×5%=270名.
答:估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数为270名.
22.(12分)某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润 B型利润
甲店 200 170
乙店 160 150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
【解答】解:依题意,分配给甲店A型产品x件,则甲店B型产品有(70﹣x)件,乙店A型有(40﹣x)件,B型有{30﹣(40﹣x)}件,则
(1)W=200x+170(70﹣x)+160(40﹣x)+150(x﹣10)=20x+16800.
由,解得10≤x≤40.
(2)由W=20x+16800≥17560,
∴x≥38.
∴38≤x≤40,x=38,39,40.
∴有三种不同的分配方案.
方案一:x=38时,甲店A型38件,B型32件,乙店A型2件,B型28件;
方案二:x=39时,甲店A型39件,B型31件,乙店A型1件,B型29件;
方案三:x=40时,甲店A型40件,B型30件,乙店A型0件,B型30件.
(3)依题意:200﹣a>170,即a<30,
W=(200﹣a)x+170(70﹣x)+160(40﹣x)+150(x﹣10)=(20﹣a)x+16800,(10≤x≤40).
①当0<a<20时,20﹣a>0,W随x增大而增大,
∴x=40,W有最大值,
即甲店A型40件,B型30件,乙店A型0件,B型30件,能使总利润达到最大;
②当a=20时,10≤x≤40,W=16800,符合题意的各种方案,使总利润都一样;
③当20<a<30时,20﹣a<0,W随x增大而减小,
∴x=10,W有最大值,
即甲店A型10件,B型60件,乙店A型30件,B型0件,能使总利润达到最大.
23.(12分)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题探究:
(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:
(2)若将原题中的“正方形”改为“矩形”(如图4所示),且=k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.
拓展应用:
(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
【解答】解;(1)①BG=DE,BG⊥DE;
②仍然成立,选择图2证明如下:
证明:∵四边形ABCD、CEFG都是正方形;
∴BC=CD,CG=CE,∠BCD=∠ECG,
∴∠BCG=∠DCE,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE;
(2)BG⊥DE,=k,
如图5,
证明:
∵四边形ABCD,CEFG都是矩形,且==k,
∴==k,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
∴△BCG∽△DCE,
∴∠CBG=∠CDE,=k,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE;
(3)∵BG⊥DE,
∴BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2,
又∵AB=3,CE=2,
∴BD=3,GE=2,
∴BD2+GE2=(3)2+(2)2=26,
∴BE2+DG2=26.
24.(14分)如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上.过点B、C作直线l.将直线l平移,平移后的直线l与x轴交于点D,与y轴交于点E.
(1)将直线l向右平移,设平移距离CD为t(t≥0),直角梯形OABC被直线l扫过的面积(图中阴影部分)为s,s关于t的函数图象如图2所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积,
②当2<t<4时,求S关于t的函数解析式;
(2)在第(1)题的条件下,当直线l向左或向右平移时(包括l与直线BC重合),在直线AB上是否存在点P,使△PDE为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
【解答】解:(1)①AB=2
OA==4,OC=4,S梯形OABC=12
②当2<t<4时,
直角梯形OABC被直线l扫过的面积=直角梯形OABC面积一直角三角形DOE面积,
∵AB∥CD,OA=4,
∴==,
∴OE=8﹣2t
S=12﹣(4﹣t)×(8﹣2t)=﹣t2+8t﹣4;
(2)存在
P1(﹣12,4),P2(﹣4,4),P3(﹣,4),P4(4,4),P5(8,4)
下面提供参考解法二:
以直角进行分类进行讨论(分三类):
第一类如上分析中①所示图∠P为直角:
设直线DE:y=2x+2b,此时D(﹣b,0),E(0,2b)的中点坐标为,
直线DE的中垂线方程:y﹣b=﹣,
令y=4得.
由已知可得PE=DE即
化简得3b2﹣32b+64=0
解得b1=8,b2=将之代入P(﹣8,4)
∴P1=(4,4)P2(﹣4,4);
第二类如上分析中②所示图∠E为直角:
设直线DE:y=2x+2b,此时D(﹣b,o),E(O,2b),
直线PE的方程:y=﹣,
令y=4得P(4b﹣8,4).
由已知可得PE=DE即
化简得b2=(2b﹣8)2
解之得,b1=4,b2=将之代入P(4b﹣8,4)
∴P3=(8,4)
第三类如上分析中③所示图∠D为直角:
设直线DE:y=2x+2b,此时D(﹣b,o),E(O,2b),
直线PD的方程:y=﹣(x+b),
令y=4得P(﹣b﹣8,4).
由已知可得PD=DE即
解得b1=4,b2=﹣4将之代入P(﹣b﹣8,4)
∴P5=(﹣12,4)、P6(﹣4,4)、[P6(﹣4,4)与P2重合舍去].
综上可得P点的坐标共5个解,分别为P(﹣12,4)、P(﹣4,4)、P(﹣,4)、
P(8,4)、P(4,4).
事实上,我们可以得到更一般的结论:
如果得出AB=a、OC=b、OA=h、设,则P点的情形如下:
第1页(共1页)
同课章节目录
