人教版八年级下册第十八章 平行四边形 章末复习题(含答案)
文档属性
| 名称 | 人教版八年级下册第十八章 平行四边形 章末复习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 16:45:05 | ||
图片预览



文档简介
第十八章 平行四边形
章末复习题
一、选择题
1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( )
A.AB∥CD B.AD=BC C.∠A=∠B D.∠A=∠D
2.如图,在四边形ABCD中,AD∥BC,BC=2AD,AC为一条对角线,且∠BAC=90°,E为BC的中点,连接AE.下列结论不正确的是( )
A.AE=BE B.AE∥DC C.AB=DC D.AE=DC
3.如图,两张宽为3的长方形纸条叠放在一起,已知∠ABC=60°,则阴影部分的面积是( )
A. B.3 C. D.6
4.已知四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC的度数为( )
A.30° B.150° C.30°或150° D.30°或120°
5.如图,在 ABCD中,AB=8,∠ABC=60°,BE平分∠ABC,交边AD于点E,连接CE.若AE=2ED,则CE的长为( )
A.6 B.4 C.4 D.2
6.如图,在 ABCD中,∠ABC=60°,BD为对角线,将△BCD沿CD方向平移,使得BC与AD重合,点D的对应点为E,过点E作EF⊥BC,交BC的延长线于点F,则下列说法正确的是( )
A.AE=BF B.BD平分∠ABC C.∠DAE=30° D.CF=DE
7.如图,P是面积为S的 ABCD内任意一点,△PAD的面积为S1,△PBC的面积为S2,则( )
A.S1+S2> B.S1+S2< C.S1+S2= D.S1+S2的大小与P点位置有关
8.七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( )
图1 图2
A.1和1 B.1和2 C.2和1 D.2和2
二、填空题
9.已知第1个三角形的周长为1,连接三边的中点构成第2个三角形,再连接第2个三角形三边的中点构成第3个三角形,……依此类推,第2024个三角形的周长是 .
10.如图,在矩形ABCD中,点E在边BC上,F是AE的中点,AB=8,AD=DE=10,则BF的长为 .
11.如图,E,F分别是矩形ABCD的边CD,AB的中点,两条平行线AK,CL分别经过菱形EGFH的顶点H,G和边FG,EH的中点M,N.已知菱形EGFH的面积为S,则图中阴影部分的面积和为 .(用含S的代数式表示)
12.将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图1;再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE,DF,如图2.解决下列问题:
(1)四边形AEDF 菱形;(填“是”或“不是”)
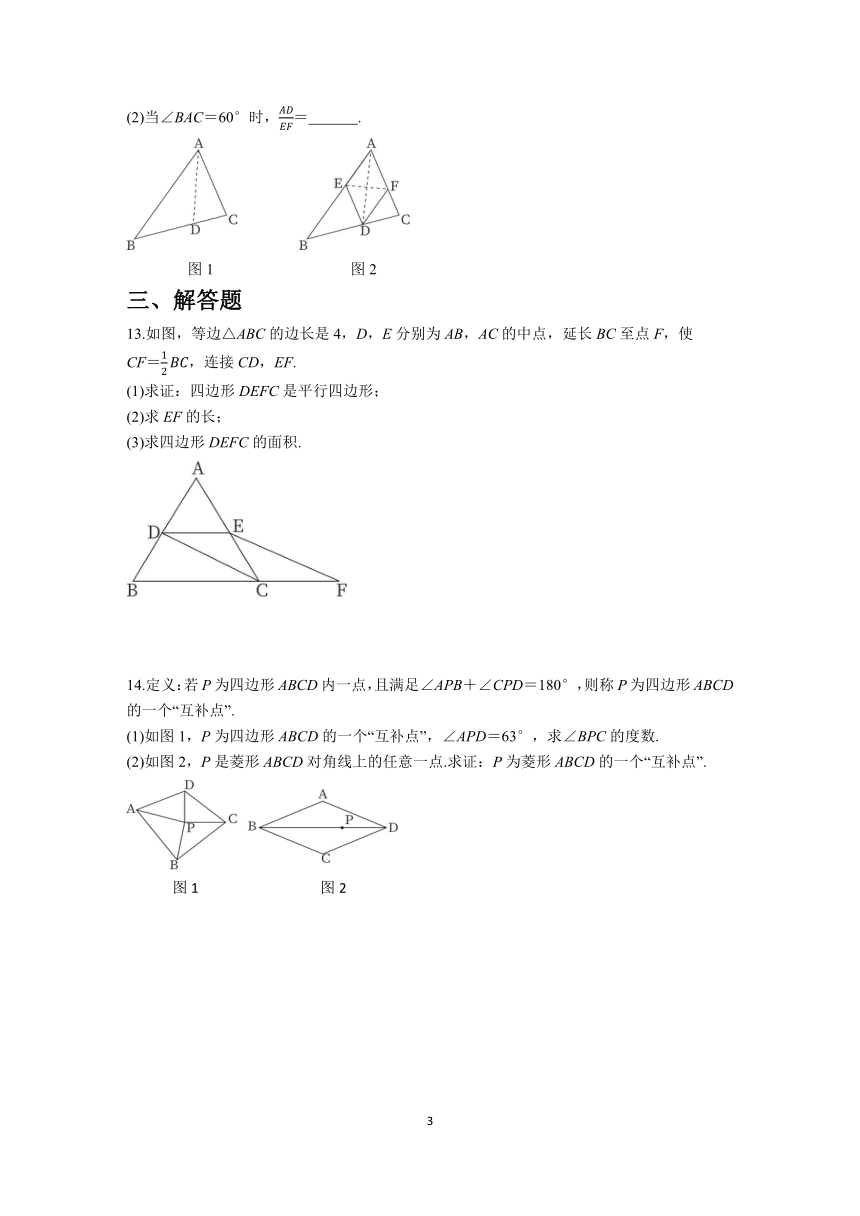
(2)当∠BAC=60°时,= .
图1 图2
三、解答题
13.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使
CF=,连接CD,EF.
(1)求证:四边形DEFC是平行四边形;
(2)求EF的长;
(3)求四边形DEFC的面积.
14.定义:若P为四边形ABCD内一点,且满足∠APB+∠CPD=180°,则称P为四边形ABCD的一个“互补点”.
(1)如图1,P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.
(2)如图2,P是菱形ABCD对角线上的任意一点.求证:P为菱形ABCD的一个“互补点”.
图1 图2
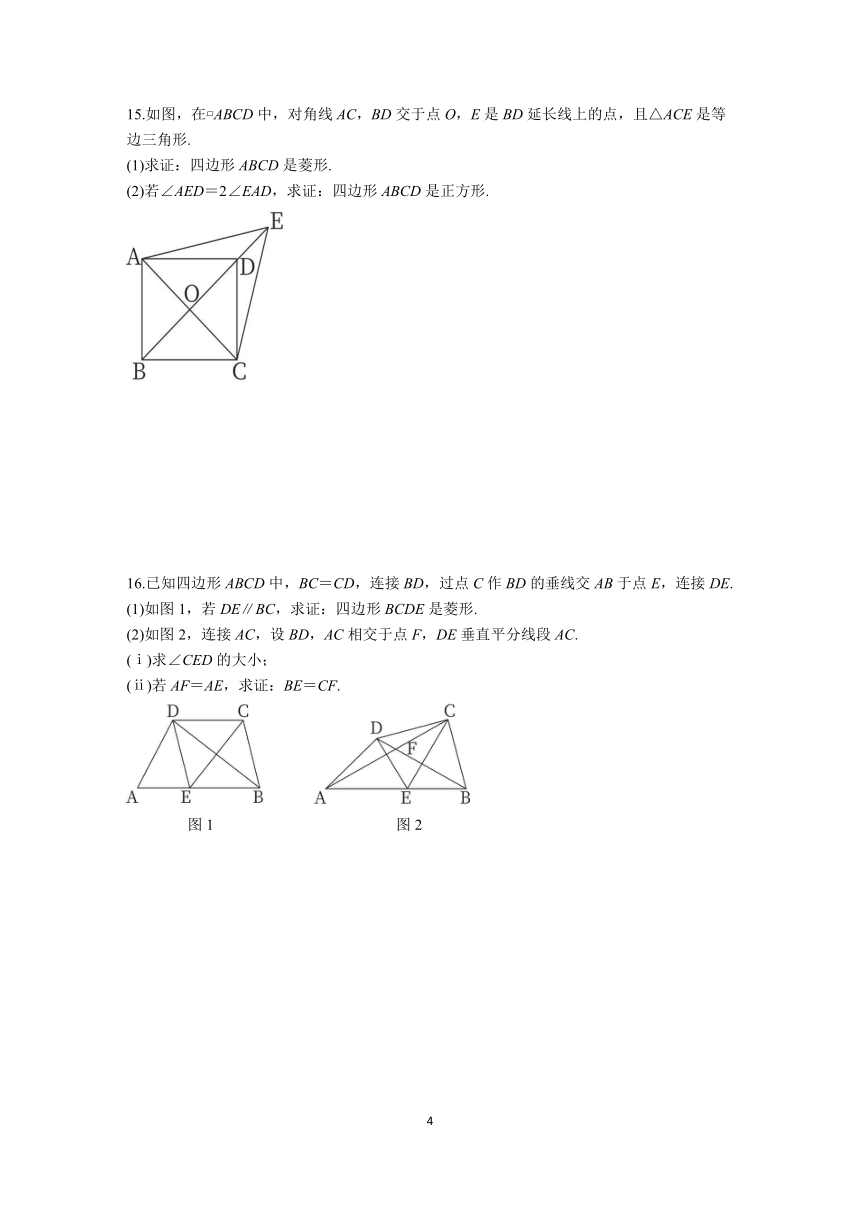
15.如图,在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
16.已知四边形ABCD中,BC=CD,连接BD,过点C作BD的垂线交AB于点E,连接DE.
(1)如图1,若DE∥BC,求证:四边形BCDE是菱形.
(2)如图2,连接AC,设BD,AC相交于点F,DE垂直平分线段AC.
(ⅰ)求∠CED的大小;
(ⅱ)若AF=AE,求证:BE=CF.
图1 图2
17.如图,四边形ABCD是平行四边形,连接AC,BD交于点O,DE平分∠ADB交AC于点E,BF平分∠CBD交AC于点F,连接BE,DF.
(1)求证:∠1=∠2;
(2)若四边形ABCD是菱形且AB=2,∠ABC=120°,求四边形BEDF的面积.
1
参考答案
一、选择题
1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( C )
A.AB∥CD B.AD=BC C.∠A=∠B D.∠A=∠D
2.如图,在四边形ABCD中,AD∥BC,BC=2AD,AC为一条对角线,且∠BAC=90°,E为BC的中点,连接AE.下列结论不正确的是( C )
A.AE=BE B.AE∥DC C.AB=DC D.AE=DC
3.如图,两张宽为3的长方形纸条叠放在一起,已知∠ABC=60°,则阴影部分的面积是( D )
A. B.3 C. D.6
4.已知四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC的度数为( C )
A.30° B.150° C.30°或150° D.30°或120°
5.如图,在 ABCD中,AB=8,∠ABC=60°,BE平分∠ABC,交边AD于点E,连接CE.若AE=2ED,则CE的长为( C )
A.6 B.4 C.4 D.2
6.如图,在 ABCD中,∠ABC=60°,BD为对角线,将△BCD沿CD方向平移,使得BC与AD重合,点D的对应点为E,过点E作EF⊥BC,交BC的延长线于点F,则下列说法正确的是( D )
A.AE=BF B.BD平分∠ABC C.∠DAE=30° D.CF=DE
7.如图,P是面积为S的 ABCD内任意一点,△PAD的面积为S1,△PBC的面积为S2,则( C )
A.S1+S2> B.S1+S2< C.S1+S2= D.S1+S2的大小与P点位置有关
8.七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( D )
图1 图2
A.1和1 B.1和2 C.2和1 D.2和2
二、填空题
9.已知第1个三角形的周长为1,连接三边的中点构成第2个三角形,再连接第2个三角形三边的中点构成第3个三角形,……依此类推,第2024个三角形的周长是 .
【答案】
10.如图,在矩形ABCD中,点E在边BC上,F是AE的中点,AB=8,AD=DE=10,则BF的长为 .
【答案】2
11.如图,E,F分别是矩形ABCD的边CD,AB的中点,两条平行线AK,CL分别经过菱形EGFH的顶点H,G和边FG,EH的中点M,N.已知菱形EGFH的面积为S,则图中阴影部分的面积和为 .(用含S的代数式表示)
【答案】
12.将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图1;再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE,DF,如图2.解决下列问题:
(1)四边形AEDF 菱形;(填“是”或“不是”)
(2)当∠BAC=60°时,= .
图1 图2
【答案】是
三、解答题
13.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使
CF=,连接CD,EF.
(1)求证:四边形DEFC是平行四边形;
(2)求EF的长;
(3)求四边形DEFC的面积.
解:(1)证明略.
(2)EF=2.
(3)S四边形DEFC=2.
14.定义:若P为四边形ABCD内一点,且满足∠APB+∠CPD=180°,则称P为四边形ABCD的一个“互补点”.
(1)如图1,P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.
(2)如图2,P是菱形ABCD对角线上的任意一点.求证:P为菱形ABCD的一个“互补点”.
图1 图2
解:(1)∠BPC=117°.
(2)连接AP,CP.
∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CDP.
易证△ADP≌△CDP,∴∠APD=∠CPD.
∵∠APB+∠APD=180°,
∴∠APB+∠CPD=180°,
∴P为菱形ABCD的一个“互补点”.
15.如图,在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC.
∵△ACE是等边三角形,
∴EO⊥AC,即BD⊥AC.
又∵四边形ABCD是平行四边形,
∴ ABCD是菱形.
(2)∵△ACE是等边三角形,∴∠AEC=60°.
由(1)知,EO⊥AC,OA=OC,
∴∠AED=∠CED=30°,∠AOE=90°,
∴∠EAO=60°.
∵∠AED=2∠EAD,∴∠EAD=15°,
∴∠DAO=∠EAO-∠EAD=45°.
∵ ABCD是菱形,
∴∠BAD=2∠DAO=90°,
∴菱形ABCD是正方形.
16.已知四边形ABCD中,BC=CD,连接BD,过点C作BD的垂线交AB于点E,连接DE.
(1)如图1,若DE∥BC,求证:四边形BCDE是菱形.
(2)如图2,连接AC,设BD,AC相交于点F,DE垂直平分线段AC.
(ⅰ)求∠CED的大小;
(ⅱ)若AF=AE,求证:BE=CF.
图1 图2
解:(1)∵DE∥BC,∴∠BDE=∠CBD.
∵BC=CD,∴∠BDC=∠CBD,
∴∠BDE=∠BDC.
又∵BD⊥CE,∴CD=DE,
∴BC=CD=DE.
∵BC∥DE,∴四边形BCDE是平行四边形.
又∵BC=CD,∴四边形BCDE是菱形.
(2)(ⅰ)∵DE垂直平分AC,
∴AE=CE,∴∠AED=∠CED,
同理可得∠CED=∠BEC,
∴∠AED=∠CED=∠BEC.
∵∠AED+∠CED+∠BEC=180°,
∴∠CED=×180°=60°.
(ⅱ)由(ⅰ)得∠BED=∠AEC=∠AED+∠CED=120°,
且∠EDB=∠EBD=30°,∠EAC=∠ECA=30°,
∴∠AFB=120°,∴∠AEC=∠AFB,
∴△ACE≌△ABF(ASA),∴AC=AB.
又∵AE=AF,∴AB-AE=AC-AF,
即BE=CF.
17.如图,四边形ABCD是平行四边形,连接AC,BD交于点O,DE平分∠ADB交AC于点E,BF平分∠CBD交AC于点F,连接BE,DF.
(1)求证:∠1=∠2;
(2)若四边形ABCD是菱形且AB=2,∠ABC=120°,求四边形BEDF的面积.
解:(1)易得∠ADB=∠CBD.
∵∠ODE=∠ADB,∠OBF=∠CBD,
∴∠ODE=∠OBF,∴DE∥BF.
易证△ODE≌△OBF(ASA),∴DE=BF,
∴四边形BEDF是平行四边形,
∴BE∥DF,∴∠1=∠2.
(2)由(1)知四边形BEDF是平行四边形,
∵AC⊥BD,即EF⊥BD,
∴四边形BEDF是菱形.
∵AD∥BC,∠ABC=120°,∴∠BAD=60°.
∵AD=AB,∴△ABD是等边三角形,
∴BD=AB=2,∠ADO=60°,
∴OD==1.
∵∠ODE=∠ADO=30°,∴DE=2OE,
∴由DE2=OD2+DE2,得OE=(负值舍去),
∴EF=2OE=,
∴S菱形BEDF=·EF=.
章末复习题
一、选择题
1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( )
A.AB∥CD B.AD=BC C.∠A=∠B D.∠A=∠D
2.如图,在四边形ABCD中,AD∥BC,BC=2AD,AC为一条对角线,且∠BAC=90°,E为BC的中点,连接AE.下列结论不正确的是( )
A.AE=BE B.AE∥DC C.AB=DC D.AE=DC
3.如图,两张宽为3的长方形纸条叠放在一起,已知∠ABC=60°,则阴影部分的面积是( )
A. B.3 C. D.6
4.已知四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC的度数为( )
A.30° B.150° C.30°或150° D.30°或120°
5.如图,在 ABCD中,AB=8,∠ABC=60°,BE平分∠ABC,交边AD于点E,连接CE.若AE=2ED,则CE的长为( )
A.6 B.4 C.4 D.2
6.如图,在 ABCD中,∠ABC=60°,BD为对角线,将△BCD沿CD方向平移,使得BC与AD重合,点D的对应点为E,过点E作EF⊥BC,交BC的延长线于点F,则下列说法正确的是( )
A.AE=BF B.BD平分∠ABC C.∠DAE=30° D.CF=DE
7.如图,P是面积为S的 ABCD内任意一点,△PAD的面积为S1,△PBC的面积为S2,则( )
A.S1+S2> B.S1+S2< C.S1+S2= D.S1+S2的大小与P点位置有关
8.七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( )
图1 图2
A.1和1 B.1和2 C.2和1 D.2和2
二、填空题
9.已知第1个三角形的周长为1,连接三边的中点构成第2个三角形,再连接第2个三角形三边的中点构成第3个三角形,……依此类推,第2024个三角形的周长是 .
10.如图,在矩形ABCD中,点E在边BC上,F是AE的中点,AB=8,AD=DE=10,则BF的长为 .
11.如图,E,F分别是矩形ABCD的边CD,AB的中点,两条平行线AK,CL分别经过菱形EGFH的顶点H,G和边FG,EH的中点M,N.已知菱形EGFH的面积为S,则图中阴影部分的面积和为 .(用含S的代数式表示)
12.将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图1;再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE,DF,如图2.解决下列问题:
(1)四边形AEDF 菱形;(填“是”或“不是”)
(2)当∠BAC=60°时,= .
图1 图2
三、解答题
13.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使
CF=,连接CD,EF.
(1)求证:四边形DEFC是平行四边形;
(2)求EF的长;
(3)求四边形DEFC的面积.
14.定义:若P为四边形ABCD内一点,且满足∠APB+∠CPD=180°,则称P为四边形ABCD的一个“互补点”.
(1)如图1,P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.
(2)如图2,P是菱形ABCD对角线上的任意一点.求证:P为菱形ABCD的一个“互补点”.
图1 图2
15.如图,在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
16.已知四边形ABCD中,BC=CD,连接BD,过点C作BD的垂线交AB于点E,连接DE.
(1)如图1,若DE∥BC,求证:四边形BCDE是菱形.
(2)如图2,连接AC,设BD,AC相交于点F,DE垂直平分线段AC.
(ⅰ)求∠CED的大小;
(ⅱ)若AF=AE,求证:BE=CF.
图1 图2
17.如图,四边形ABCD是平行四边形,连接AC,BD交于点O,DE平分∠ADB交AC于点E,BF平分∠CBD交AC于点F,连接BE,DF.
(1)求证:∠1=∠2;
(2)若四边形ABCD是菱形且AB=2,∠ABC=120°,求四边形BEDF的面积.
1
参考答案
一、选择题
1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( C )
A.AB∥CD B.AD=BC C.∠A=∠B D.∠A=∠D
2.如图,在四边形ABCD中,AD∥BC,BC=2AD,AC为一条对角线,且∠BAC=90°,E为BC的中点,连接AE.下列结论不正确的是( C )
A.AE=BE B.AE∥DC C.AB=DC D.AE=DC
3.如图,两张宽为3的长方形纸条叠放在一起,已知∠ABC=60°,则阴影部分的面积是( D )
A. B.3 C. D.6
4.已知四边形ABCD为菱形,该菱形的周长为16,面积为8,则∠ABC的度数为( C )
A.30° B.150° C.30°或150° D.30°或120°
5.如图,在 ABCD中,AB=8,∠ABC=60°,BE平分∠ABC,交边AD于点E,连接CE.若AE=2ED,则CE的长为( C )
A.6 B.4 C.4 D.2
6.如图,在 ABCD中,∠ABC=60°,BD为对角线,将△BCD沿CD方向平移,使得BC与AD重合,点D的对应点为E,过点E作EF⊥BC,交BC的延长线于点F,则下列说法正确的是( D )
A.AE=BF B.BD平分∠ABC C.∠DAE=30° D.CF=DE
7.如图,P是面积为S的 ABCD内任意一点,△PAD的面积为S1,△PBC的面积为S2,则( C )
A.S1+S2> B.S1+S2< C.S1+S2= D.S1+S2的大小与P点位置有关
8.七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( D )
图1 图2
A.1和1 B.1和2 C.2和1 D.2和2
二、填空题
9.已知第1个三角形的周长为1,连接三边的中点构成第2个三角形,再连接第2个三角形三边的中点构成第3个三角形,……依此类推,第2024个三角形的周长是 .
【答案】
10.如图,在矩形ABCD中,点E在边BC上,F是AE的中点,AB=8,AD=DE=10,则BF的长为 .
【答案】2
11.如图,E,F分别是矩形ABCD的边CD,AB的中点,两条平行线AK,CL分别经过菱形EGFH的顶点H,G和边FG,EH的中点M,N.已知菱形EGFH的面积为S,则图中阴影部分的面积和为 .(用含S的代数式表示)
【答案】
12.将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片,如图1;再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE,DF,如图2.解决下列问题:
(1)四边形AEDF 菱形;(填“是”或“不是”)
(2)当∠BAC=60°时,= .
图1 图2
【答案】是
三、解答题
13.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使
CF=,连接CD,EF.
(1)求证:四边形DEFC是平行四边形;
(2)求EF的长;
(3)求四边形DEFC的面积.
解:(1)证明略.
(2)EF=2.
(3)S四边形DEFC=2.
14.定义:若P为四边形ABCD内一点,且满足∠APB+∠CPD=180°,则称P为四边形ABCD的一个“互补点”.
(1)如图1,P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.
(2)如图2,P是菱形ABCD对角线上的任意一点.求证:P为菱形ABCD的一个“互补点”.
图1 图2
解:(1)∠BPC=117°.
(2)连接AP,CP.
∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CDP.
易证△ADP≌△CDP,∴∠APD=∠CPD.
∵∠APB+∠APD=180°,
∴∠APB+∠CPD=180°,
∴P为菱形ABCD的一个“互补点”.
15.如图,在 ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC.
∵△ACE是等边三角形,
∴EO⊥AC,即BD⊥AC.
又∵四边形ABCD是平行四边形,
∴ ABCD是菱形.
(2)∵△ACE是等边三角形,∴∠AEC=60°.
由(1)知,EO⊥AC,OA=OC,
∴∠AED=∠CED=30°,∠AOE=90°,
∴∠EAO=60°.
∵∠AED=2∠EAD,∴∠EAD=15°,
∴∠DAO=∠EAO-∠EAD=45°.
∵ ABCD是菱形,
∴∠BAD=2∠DAO=90°,
∴菱形ABCD是正方形.
16.已知四边形ABCD中,BC=CD,连接BD,过点C作BD的垂线交AB于点E,连接DE.
(1)如图1,若DE∥BC,求证:四边形BCDE是菱形.
(2)如图2,连接AC,设BD,AC相交于点F,DE垂直平分线段AC.
(ⅰ)求∠CED的大小;
(ⅱ)若AF=AE,求证:BE=CF.
图1 图2
解:(1)∵DE∥BC,∴∠BDE=∠CBD.
∵BC=CD,∴∠BDC=∠CBD,
∴∠BDE=∠BDC.
又∵BD⊥CE,∴CD=DE,
∴BC=CD=DE.
∵BC∥DE,∴四边形BCDE是平行四边形.
又∵BC=CD,∴四边形BCDE是菱形.
(2)(ⅰ)∵DE垂直平分AC,
∴AE=CE,∴∠AED=∠CED,
同理可得∠CED=∠BEC,
∴∠AED=∠CED=∠BEC.
∵∠AED+∠CED+∠BEC=180°,
∴∠CED=×180°=60°.
(ⅱ)由(ⅰ)得∠BED=∠AEC=∠AED+∠CED=120°,
且∠EDB=∠EBD=30°,∠EAC=∠ECA=30°,
∴∠AFB=120°,∴∠AEC=∠AFB,
∴△ACE≌△ABF(ASA),∴AC=AB.
又∵AE=AF,∴AB-AE=AC-AF,
即BE=CF.
17.如图,四边形ABCD是平行四边形,连接AC,BD交于点O,DE平分∠ADB交AC于点E,BF平分∠CBD交AC于点F,连接BE,DF.
(1)求证:∠1=∠2;
(2)若四边形ABCD是菱形且AB=2,∠ABC=120°,求四边形BEDF的面积.
解:(1)易得∠ADB=∠CBD.
∵∠ODE=∠ADB,∠OBF=∠CBD,
∴∠ODE=∠OBF,∴DE∥BF.
易证△ODE≌△OBF(ASA),∴DE=BF,
∴四边形BEDF是平行四边形,
∴BE∥DF,∴∠1=∠2.
(2)由(1)知四边形BEDF是平行四边形,
∵AC⊥BD,即EF⊥BD,
∴四边形BEDF是菱形.
∵AD∥BC,∠ABC=120°,∴∠BAD=60°.
∵AD=AB,∴△ABD是等边三角形,
∴BD=AB=2,∠ADO=60°,
∴OD==1.
∵∠ODE=∠ADO=30°,∴DE=2OE,
∴由DE2=OD2+DE2,得OE=(负值舍去),
∴EF=2OE=,
∴S菱形BEDF=·EF=.
