2022~2023学年内蒙古呼伦贝尔满洲里市满洲里远方中学高二下学期期末理科数学试卷(PDF版含解析)
文档属性
| 名称 | 2022~2023学年内蒙古呼伦贝尔满洲里市满洲里远方中学高二下学期期末理科数学试卷(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 17:44:59 | ||
图片预览




文档简介
2022~2023学年内蒙古呼伦贝尔满洲里市满洲里远方中学高二下学期期末
理科数学试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则 =( )
A.
B.
C.
D.
2、已知复数 ,则 i ( )
i
A.
B.
C.
D.
3、“直线 + + =0与圆 相切”是“ =1”的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
4、从某小区抽取50户居民进行月用电量调查,发现用电量均在50度到350度之间,频率分布直方图如下图所
示.则在这些用户中,用电量在区间 , 内有( )户
A.26
B.30
C.35
D.41
5、函数 的图像可能是( )
A.
B.
C.
D.
6、直播带货是一种直播和电商相结合的销售手段,目前受到了广大消费者的追捧,针对这种现状,某传媒公司
决定逐年加大直播带货的资金投入,若该公司今年投入的资金为 万元,并在此基础上,以后每年的资金投
入均比上一年增长 ,则该公司需经过( )年其投入资金开始超过 万元.
(参考数据: , , )
A.
B.
C.
D.
7、若 展开式中各项系数之和为 ,则该展开式中含 的项的系数为( )
A.
B.256
C. 320
D.
8、已知函数
为奇函数,该函数的部分图象如图所示, 是边长
为2的等边三角形,则 的值为
A.
B.
C.
D.
9、若数列 满足 ,则称 为“梦想数列”,已知正项数列 为“梦想数列”,且
,则 ( )
A. =2
B. =2
C. =2 +1
D. =2 +1
10、已知四棱锥 中,平面 平面ABCD,其中 为正方形, 是边长为2的等边三角
形,则四棱锥 外接球的表面积为( )
A.4
B.
C.
D.
11、已知抛物线 : 的焦点 的坐标为 , ,准线与 轴交于点 ,点 在第一象限且在抛物线
上,则当 取得最大值时,直线 的方程为( )
A.
B.
C. = +2
D.
12、若对 , , ,且 ,都有 ,则 的最大值是( )
A.
e
B.e
C.
D.
e
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知向量 , 满足 , ,则 .
14、已知 中,已知 , 的面积 ,则边长 的值为 .
15、函数 且 的图象恒过定点 ,若点 在直线 上,其中
,则 + 的最小值为 .
16、如图, , 是椭圆 与双曲线 的公共焦点, , 分别是 , 在第二、四象限的公共点,若
,且 ,则 与 的离心率之积为 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知在等差数列 中, , .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
18、(本小题8分)
随着数字化信息技术的发展,网络成了人们生活的必需品,它一方面给人们的生活带来了极大的便利,节约了
资源和成本,另一方面青少年沉迷网络现象也引起了整个社会的关注和担忧,为了解当前大学生每天上网情
况,某调查机构对某高校男生、女生各50名学生进行了调查,其中每天上网的时间超过8小时的被称为“有网
瘾”,否则被称为“无网瘾”.调查结果如下:
有网瘾 无网瘾 合计
女生 10
男生 20
合计 100
(1)将上面的2×2列联表补充完整,再判断是否有 的把握认为“有网瘾”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“有 网
瘾”的人数为X,试求X的分布列与数学期望.
参考公式: ,其中
参考数据:
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
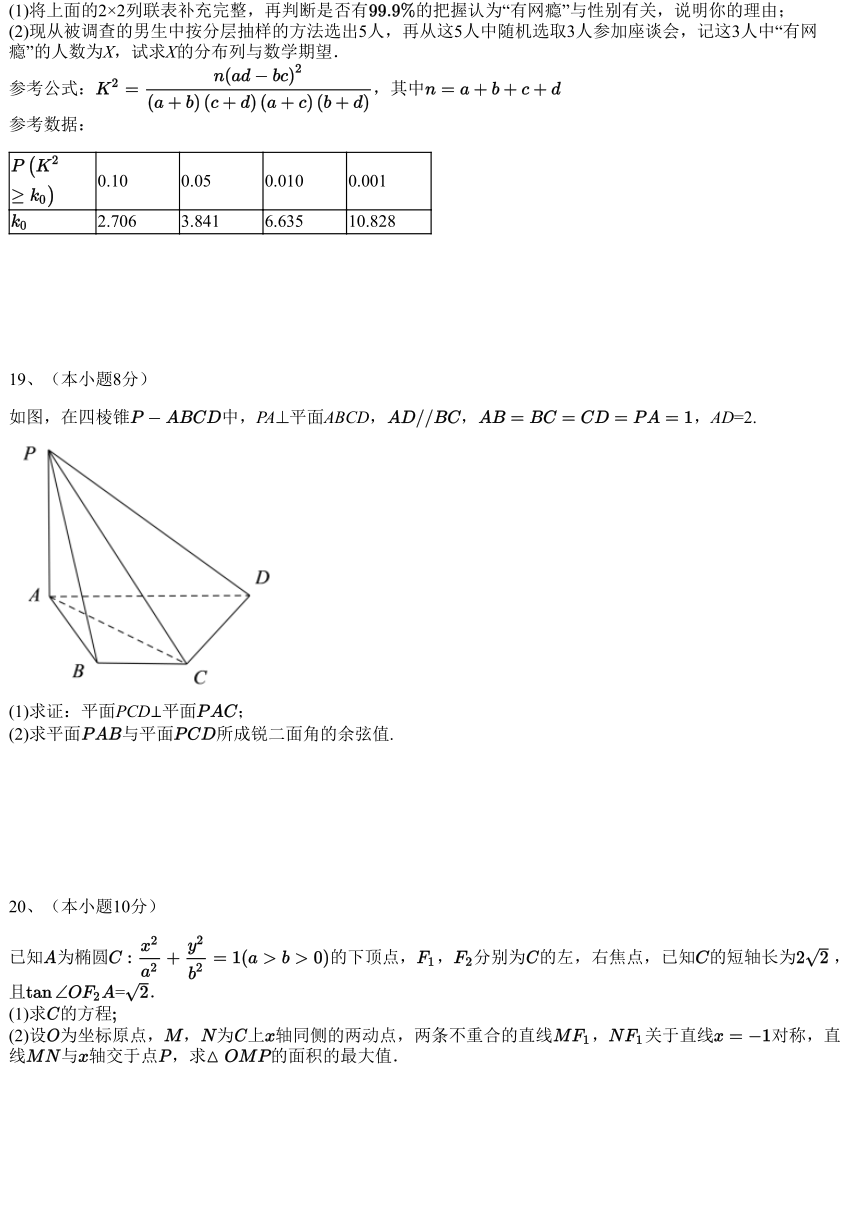
19、(本小题8分)
如图,在四棱锥 中,PA 平面ABCD, , ,AD=2.
(1)求证:平面PCD⊥平面 ;
(2)求平面 与平面 所成锐 二面角的余弦值.
20、(本小题10分)
已知 为椭圆 的下顶点, , 分别为 的左,右焦点,已知 的短轴长为 ,
且 = .
(1)求 的方程
(2)设 为坐标原 点, , 为 上 轴同侧的两动点,两条不重合的直线 , 关于直线 对称,直
线 与 轴交于点 ,求 的面积的最大值.
21、(本小题12分)
已知函数 .
(1)当 时,求函数 的单调区间;
(2)若不等式 对于任意 成立,求正实数 的取值范围.
22、(本小题12分)
在平面直角坐标系 中,过点 的直线 的参数方程为 ( 为参数).以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
(1)求直线 的普通方程和曲线 的直角坐标方程;
(2)设曲线 与直线 交于 两点,求 的值.
23、(本小题12分)
设函数 .
(1)求不等式 的解集;
(2)若 的最小值是 ,且 ,求 的最小值.
参考答案
一、单选题
1、
【答 案】
D
【分析】
根据集合的交集的运算求出答案即可.
【详解】
解: , ,
.
故选:D.
2、
【答 案】
C
【分析】
利用复数的除法运算求出复数z,再利用复数模的意义计算作答.
【详解】
i) i)
依题意, i,则 i i,
i) i)
所以 i .
故选:C
3、
【答 案】
A
【分析】
根据充分必要条件的定义推理即可求解.
【详解】
依题意, ,即圆心是(1,0),半径为 ,
如果直线x+y+m=0是此圆的切线,则圆心到直线的距离为 ,
即 或-3,
所以“直线x+y+m=0与圆 相切”不是m=1的充分条件;
如果m=1,则直线为x+y+1=0,圆心(1,0)到直线的距离为 ,即相切,
是必要条件;
故选:A.
4、
【答 案】
C
【分析】
先利用频率之和为1求出 ,进而求出电量在区间 , 内的户数.
【详解】
由题意得 : ,
解得: ,
则电量在区间 , 内有 (户).
故选:C
5、
【答 案】
D
【分析】
设 ,则 ,
故 是奇函数,排除A、B,又 ,故排除C.
因此正确答案为:D.
6、
【答 案】
C
【分析】
设该公司经过 年投入的资金为 万元,则 ,
通过题意可知,数列 是以 为首项,以 为公比 的等比数列,
所以, ,由 可得 ,
因此,该公司需经过 年其投入资金开始超过 万元.
因此正确答案为:C.
7、
【答 案】
A
【分析】
令 ,则 .
展开式的通项为 C C
令 ,所以含 的项的系数为 C .
因此正确答案为:A
8、
【答 案】
D
【分析】
【详解】
由f (x)=Acos(ωx+φ)为奇函数,利用奇函数的性质可得f(0)=Acosφ=0结合已知0<φ<π,可求 φ=
再由△EFG是边长为2的等边三角形,可得yE= =A,结合图象可得,函数的周期 T=4,根据周期公式可得,
ω,从而可得f(x),代入可求f(1).
解:∵f(x)=Acos(ωx+φ)为奇函数
∴f(0)=Acosφ=0
∵0<φ<π∴φ=π/2
∴f(x)=Acos(ωx+ )=-Asinωx
∵△EFG是边长为2的等边三角形,则yE= =A
又∵函数的周期 T=2FG=4,根据周期公式可得,
( ) A\sin
则 ( )
故选
9、
【答 案】
B
【分析】
将 作为整体代入,即可求解.
【详解】
依题意, ,
即 是首项为2,公比为3 的等比数列, ;
故选:B.
10、
【答案 】
B
【分析】
连接 交 于 ,球心 在底面的射影必为点 ,取 的中点 ,在截面 中,利用勾股定理求出球的半
径,即可求四棱锥 的外接球的表面积.
【详解】
连接 交 于 ,球心 在底面的射影必为点 ,取 的中点 ,在截面 中,连接 ,如图,
在等边 中, 的中点为 ,
所以 ,又平面 平面 , 是交线,
所以 平面 ,且 ,
设 ,外接球半径为 ,
则在正方形 中, , ,
在Rt 中, ,
而在截面 中, ,
由 可得:
解得 ,
所以 ,
所以 .
故选:B.
11、
【答 案】
C
【分析】
解:过M作MP与准线垂直,垂足为P,则 ,则当 取得最大
值,则∠MAF必须取得最大值,此时AM与抛物线相切,
因为抛物线 : 的焦点 的坐标为 , ,所以 .
设切线方程为y=k(x+2),则 ,ky2﹣8y+16k=0,
Δ=64﹣64k2=0,k2=1,则k=±1,
因为点 在第一象限且在抛物线 上 ,所以 .
则直线方程y=x+2.
因此正确答案为:C
12、
【答 案】
A
【分析】
将原问题转化为求函数的单调性即可.
【详解】
由题意, ,
令 ,则有 , ,
,
,
即函数 是增函数,
e , e ,
e
故选:A.
二、填空题
13、
【答案 】
4
【分析】
由垂直关系得到 ,利用向量数量积运算法则进行计算.
【详解】
因为 ,所以 ,所以
故答案为:4
14、
【答 案】
5
【分析】
利用三角形面积公式可得 ,然后利用余弦定理即得.
【详解】
设 中三角所对边为 ,则 ,
∵ ,
∴ ,
由余弦定理可得, ,
解得 ,即 .
故答案为:5.
15、
【答 案】
9
【分析】
∵ 恒过定点 ,
∴ 过定点
∴ ,即 ,
∴ ≥ ,
当且仅当 即 时等号成立,
∴所以 + 的最小值为9,
因此正确答案为:9.
16、
【答 案】
2
【分析】
根据已知条件结合椭圆的对称性可求出 , ,再根据椭圆和双曲线的定义以及离心率公式
求出离心率即可求解.
【详解】
解:连接 ,根据椭圆的对称性可知:点 是 的中点,
所以,四边形 为平行四边形,
若 ,所以 ,
因为 ,所以 ,所以 是等边三角形,
所以 , , ,
所以,四边形 为矩形,
所以,在直角三角形 中, ,
所以, ,
在椭圆中, ,可得
在双曲线中, ,可得
所以离心率之积 ,
故答案为: .
三、解答题
17、
【答案 】
(1)
(2)
【分析】
(1)设等差数列 的公差为 ,根据条件可得 ,解出即可得答案;
(2)利用裂项相消法求出答案即可.
【详解】
(1)设等 差数列 的公差为 ,
由 ,可得
解得 ,
所以
(2)由(1)可得
所以
18、
【答案 】
(1)列联表见解析,有 的把握认为“有网瘾”与性别有关
(2)分布列详见解析,
【分析】
(1)由题意,完成2×2列联表,然后根据参考公式计算出 并结合临界值表即可求解;
(2)根据超几何分布即可求出X的分布列,由期望公式即可求解X的数学期望.
【详解】
(1)解: 根据题意,列联表如下:
有网瘾 无网瘾 合计
女生 40 10 50
男生 20 30 50
合计 60 40 100
,
所以有 的把握认为“有网瘾”与性别有关;
(2)解:由题意,“有网瘾”中抽取 (人) “无网瘾”中抽取
(人),
X的所有可能取值为0,1,2,
, , ,
所以随机变量X的分布列为:
X 0 1 2
P
故 .
19、
【答 案】
(1)证明见解析;
(2) .
【分析】
(1)取 的中点 ,连接 ,证明 , ,由线面垂直判定定理知 平面 ,再由面面
垂直的判定定理得证;
(2)建立空间直角坐标 系,利用向量法求解即可.
【详解】
(1)取 的中点 ,连接 ,如图,
因为AD//BC,AB=BC=CD=1,AD=2,所以 , ∥ ,
所以四边形 为平行四边形,
所以 ,所以 ,
因为 平面 , 平面 ,所以 ,
因为 ,所以 平面 ,
因为 平面 ,所以平面 平面 .
(2)过点 作 于 ,以 为原点,建立空 间直角坐标系,如图所示,
在等腰梯形中 ,AD//BC,AB=BC=CD=1,AD=2,
则 ,
所以 , ,
设平面 的法向量为 ,因为 ,
所以 ,令 ,则 ,
设平面 的法向量为 ,因为 ,
所以 ,令 ,则 ,
所以 .
20、
【答 案】
(1)
(2)
【分析】
(1)根据短轴长为 , 可求出 , ,再根据椭圆定义可求出 ,得到椭圆方程;
(2)直线 , 关于直线 对称,转化成 ,代入韦达定理求出 过定点
, ,再求 的面积的最大值.
【详解】
(1)(1)由题意可得
故 , , = + =3,故椭圆 的方程为 ;
(2)设 , , , ,
由 知 , ,所以直线 过点 ,因为两条不重合的直线 , 关于直线 对称,所以
, ,且 , 不同时为 的左,右顶点,设直线 的方程为 ,由
,得 ,则 , , 因为
直线 , 关于直线 对称
所以 ,则
,
所以 ,
即 , 因为 ,所以 ,
所以直线 恒过定点 , ,且 ,
当 与 的上顶点或下顶点重合,即 时, 的面积的最大,
即最大值为 .
21、
【答案 】
(1)递增区间为 ,递减区间为
(2) .
【分析】
(1)由导数得出函数 的单调区间;
(2)设 ,由导数得出 ,再由
得出 ,最后由导数解不等式 得出正实数 的取值范围.
【详解】
(1)函数 的定义域为 ,
当 或 时, , 单调递增;
当 时, , 单调递减,
故函数 的单调递增区间为
函数 的单调递减区间为 .
(2)原题等价于对任意 ,有 恒成立,
设 , ,所以
,令 ,得 ;令 ,得 ,
所以函数 在 , 上单调递减,在 上单调递增
设
则
所以 在 , 上单调递增,故 ,所以 ,
从而 , 所以 ,即 ,
设 ,则 ,
所以 在 , 上单调递增,
又 ,所以 的解为 ,
因为 ,所以正实数 的取值范围为 , .
【点睛】
关键点睛: 在问题二中,关键是将不等式的恒成立问题,转化为 ,再解不等式
得出正实数 的取值范围.
22、
【答案 】
(1) , ;
(2) .
【分析】
(1)消去 t 可得直线在直角坐标系的方程,运用极坐标与直角坐标的关系,可得曲线C的直角坐标方程;
(2)理解参数方程中 t 的意义,联立C与直线方程,应用韦达定理即可.
【详解】
(1)对于直线 ,消去 t 得 ;
由于 ,曲线C的方程为 ,
所以 ,即 ;
(2)联立方程 ,得 ,
设 和 对应的参数为 和 ,
由韦达定理 ,以及 t 的几何意义得:
= = = .
23、
【答 案】
(1) 或 ;(2) .
【分析】
(1)分类讨论 , 和 三种情况,求解 ,最后求并集即可;(2)根据(1)可
得 ,可得 ,利用柯西不等式求出 的最小值即可.
【详解】
(1)当 时, ,解得 ;
当 时, ,解得 ;
当 时, ,解得 .
综上,不等式 的解集为 或 .
(2)由(1)可知当 时, ,即 ,则 .
因为 ,
所以 ,即 (当且仅当 时等号成立).
故 的最小值为 .
【点睛】
方法点睛 :绝对值不等式的解法一般有:
法一:利用绝对值不等式的几何意义求解 ,体现了数形结合的思想;
法二:利用“零点分段法”求解,体现了分类讨论的思想;
法三:通过构造函数,利用函数的图象求解,体现了函数 与方程的思想.
理科数学试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则 =( )
A.
B.
C.
D.
2、已知复数 ,则 i ( )
i
A.
B.
C.
D.
3、“直线 + + =0与圆 相切”是“ =1”的( )
A.必要不充分条件
B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
4、从某小区抽取50户居民进行月用电量调查,发现用电量均在50度到350度之间,频率分布直方图如下图所
示.则在这些用户中,用电量在区间 , 内有( )户
A.26
B.30
C.35
D.41
5、函数 的图像可能是( )
A.
B.
C.
D.
6、直播带货是一种直播和电商相结合的销售手段,目前受到了广大消费者的追捧,针对这种现状,某传媒公司
决定逐年加大直播带货的资金投入,若该公司今年投入的资金为 万元,并在此基础上,以后每年的资金投
入均比上一年增长 ,则该公司需经过( )年其投入资金开始超过 万元.
(参考数据: , , )
A.
B.
C.
D.
7、若 展开式中各项系数之和为 ,则该展开式中含 的项的系数为( )
A.
B.256
C. 320
D.
8、已知函数
为奇函数,该函数的部分图象如图所示, 是边长
为2的等边三角形,则 的值为
A.
B.
C.
D.
9、若数列 满足 ,则称 为“梦想数列”,已知正项数列 为“梦想数列”,且
,则 ( )
A. =2
B. =2
C. =2 +1
D. =2 +1
10、已知四棱锥 中,平面 平面ABCD,其中 为正方形, 是边长为2的等边三角
形,则四棱锥 外接球的表面积为( )
A.4
B.
C.
D.
11、已知抛物线 : 的焦点 的坐标为 , ,准线与 轴交于点 ,点 在第一象限且在抛物线
上,则当 取得最大值时,直线 的方程为( )
A.
B.
C. = +2
D.
12、若对 , , ,且 ,都有 ,则 的最大值是( )
A.
e
B.e
C.
D.
e
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知向量 , 满足 , ,则 .
14、已知 中,已知 , 的面积 ,则边长 的值为 .
15、函数 且 的图象恒过定点 ,若点 在直线 上,其中
,则 + 的最小值为 .
16、如图, , 是椭圆 与双曲线 的公共焦点, , 分别是 , 在第二、四象限的公共点,若
,且 ,则 与 的离心率之积为 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知在等差数列 中, , .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
18、(本小题8分)
随着数字化信息技术的发展,网络成了人们生活的必需品,它一方面给人们的生活带来了极大的便利,节约了
资源和成本,另一方面青少年沉迷网络现象也引起了整个社会的关注和担忧,为了解当前大学生每天上网情
况,某调查机构对某高校男生、女生各50名学生进行了调查,其中每天上网的时间超过8小时的被称为“有网
瘾”,否则被称为“无网瘾”.调查结果如下:
有网瘾 无网瘾 合计
女生 10
男生 20
合计 100
(1)将上面的2×2列联表补充完整,再判断是否有 的把握认为“有网瘾”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“有 网
瘾”的人数为X,试求X的分布列与数学期望.
参考公式: ,其中
参考数据:
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
19、(本小题8分)
如图,在四棱锥 中,PA 平面ABCD, , ,AD=2.
(1)求证:平面PCD⊥平面 ;
(2)求平面 与平面 所成锐 二面角的余弦值.
20、(本小题10分)
已知 为椭圆 的下顶点, , 分别为 的左,右焦点,已知 的短轴长为 ,
且 = .
(1)求 的方程
(2)设 为坐标原 点, , 为 上 轴同侧的两动点,两条不重合的直线 , 关于直线 对称,直
线 与 轴交于点 ,求 的面积的最大值.
21、(本小题12分)
已知函数 .
(1)当 时,求函数 的单调区间;
(2)若不等式 对于任意 成立,求正实数 的取值范围.
22、(本小题12分)
在平面直角坐标系 中,过点 的直线 的参数方程为 ( 为参数).以坐标原点为极点,
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
(1)求直线 的普通方程和曲线 的直角坐标方程;
(2)设曲线 与直线 交于 两点,求 的值.
23、(本小题12分)
设函数 .
(1)求不等式 的解集;
(2)若 的最小值是 ,且 ,求 的最小值.
参考答案
一、单选题
1、
【答 案】
D
【分析】
根据集合的交集的运算求出答案即可.
【详解】
解: , ,
.
故选:D.
2、
【答 案】
C
【分析】
利用复数的除法运算求出复数z,再利用复数模的意义计算作答.
【详解】
i) i)
依题意, i,则 i i,
i) i)
所以 i .
故选:C
3、
【答 案】
A
【分析】
根据充分必要条件的定义推理即可求解.
【详解】
依题意, ,即圆心是(1,0),半径为 ,
如果直线x+y+m=0是此圆的切线,则圆心到直线的距离为 ,
即 或-3,
所以“直线x+y+m=0与圆 相切”不是m=1的充分条件;
如果m=1,则直线为x+y+1=0,圆心(1,0)到直线的距离为 ,即相切,
是必要条件;
故选:A.
4、
【答 案】
C
【分析】
先利用频率之和为1求出 ,进而求出电量在区间 , 内的户数.
【详解】
由题意得 : ,
解得: ,
则电量在区间 , 内有 (户).
故选:C
5、
【答 案】
D
【分析】
设 ,则 ,
故 是奇函数,排除A、B,又 ,故排除C.
因此正确答案为:D.
6、
【答 案】
C
【分析】
设该公司经过 年投入的资金为 万元,则 ,
通过题意可知,数列 是以 为首项,以 为公比 的等比数列,
所以, ,由 可得 ,
因此,该公司需经过 年其投入资金开始超过 万元.
因此正确答案为:C.
7、
【答 案】
A
【分析】
令 ,则 .
展开式的通项为 C C
令 ,所以含 的项的系数为 C .
因此正确答案为:A
8、
【答 案】
D
【分析】
【详解】
由f (x)=Acos(ωx+φ)为奇函数,利用奇函数的性质可得f(0)=Acosφ=0结合已知0<φ<π,可求 φ=
再由△EFG是边长为2的等边三角形,可得yE= =A,结合图象可得,函数的周期 T=4,根据周期公式可得,
ω,从而可得f(x),代入可求f(1).
解:∵f(x)=Acos(ωx+φ)为奇函数
∴f(0)=Acosφ=0
∵0<φ<π∴φ=π/2
∴f(x)=Acos(ωx+ )=-Asinωx
∵△EFG是边长为2的等边三角形,则yE= =A
又∵函数的周期 T=2FG=4,根据周期公式可得,
( ) A\sin
则 ( )
故选
9、
【答 案】
B
【分析】
将 作为整体代入,即可求解.
【详解】
依题意, ,
即 是首项为2,公比为3 的等比数列, ;
故选:B.
10、
【答案 】
B
【分析】
连接 交 于 ,球心 在底面的射影必为点 ,取 的中点 ,在截面 中,利用勾股定理求出球的半
径,即可求四棱锥 的外接球的表面积.
【详解】
连接 交 于 ,球心 在底面的射影必为点 ,取 的中点 ,在截面 中,连接 ,如图,
在等边 中, 的中点为 ,
所以 ,又平面 平面 , 是交线,
所以 平面 ,且 ,
设 ,外接球半径为 ,
则在正方形 中, , ,
在Rt 中, ,
而在截面 中, ,
由 可得:
解得 ,
所以 ,
所以 .
故选:B.
11、
【答 案】
C
【分析】
解:过M作MP与准线垂直,垂足为P,则 ,则当 取得最大
值,则∠MAF必须取得最大值,此时AM与抛物线相切,
因为抛物线 : 的焦点 的坐标为 , ,所以 .
设切线方程为y=k(x+2),则 ,ky2﹣8y+16k=0,
Δ=64﹣64k2=0,k2=1,则k=±1,
因为点 在第一象限且在抛物线 上 ,所以 .
则直线方程y=x+2.
因此正确答案为:C
12、
【答 案】
A
【分析】
将原问题转化为求函数的单调性即可.
【详解】
由题意, ,
令 ,则有 , ,
,
,
即函数 是增函数,
e , e ,
e
故选:A.
二、填空题
13、
【答案 】
4
【分析】
由垂直关系得到 ,利用向量数量积运算法则进行计算.
【详解】
因为 ,所以 ,所以
故答案为:4
14、
【答 案】
5
【分析】
利用三角形面积公式可得 ,然后利用余弦定理即得.
【详解】
设 中三角所对边为 ,则 ,
∵ ,
∴ ,
由余弦定理可得, ,
解得 ,即 .
故答案为:5.
15、
【答 案】
9
【分析】
∵ 恒过定点 ,
∴ 过定点
∴ ,即 ,
∴ ≥ ,
当且仅当 即 时等号成立,
∴所以 + 的最小值为9,
因此正确答案为:9.
16、
【答 案】
2
【分析】
根据已知条件结合椭圆的对称性可求出 , ,再根据椭圆和双曲线的定义以及离心率公式
求出离心率即可求解.
【详解】
解:连接 ,根据椭圆的对称性可知:点 是 的中点,
所以,四边形 为平行四边形,
若 ,所以 ,
因为 ,所以 ,所以 是等边三角形,
所以 , , ,
所以,四边形 为矩形,
所以,在直角三角形 中, ,
所以, ,
在椭圆中, ,可得
在双曲线中, ,可得
所以离心率之积 ,
故答案为: .
三、解答题
17、
【答案 】
(1)
(2)
【分析】
(1)设等差数列 的公差为 ,根据条件可得 ,解出即可得答案;
(2)利用裂项相消法求出答案即可.
【详解】
(1)设等 差数列 的公差为 ,
由 ,可得
解得 ,
所以
(2)由(1)可得
所以
18、
【答案 】
(1)列联表见解析,有 的把握认为“有网瘾”与性别有关
(2)分布列详见解析,
【分析】
(1)由题意,完成2×2列联表,然后根据参考公式计算出 并结合临界值表即可求解;
(2)根据超几何分布即可求出X的分布列,由期望公式即可求解X的数学期望.
【详解】
(1)解: 根据题意,列联表如下:
有网瘾 无网瘾 合计
女生 40 10 50
男生 20 30 50
合计 60 40 100
,
所以有 的把握认为“有网瘾”与性别有关;
(2)解:由题意,“有网瘾”中抽取 (人) “无网瘾”中抽取
(人),
X的所有可能取值为0,1,2,
, , ,
所以随机变量X的分布列为:
X 0 1 2
P
故 .
19、
【答 案】
(1)证明见解析;
(2) .
【分析】
(1)取 的中点 ,连接 ,证明 , ,由线面垂直判定定理知 平面 ,再由面面
垂直的判定定理得证;
(2)建立空间直角坐标 系,利用向量法求解即可.
【详解】
(1)取 的中点 ,连接 ,如图,
因为AD//BC,AB=BC=CD=1,AD=2,所以 , ∥ ,
所以四边形 为平行四边形,
所以 ,所以 ,
因为 平面 , 平面 ,所以 ,
因为 ,所以 平面 ,
因为 平面 ,所以平面 平面 .
(2)过点 作 于 ,以 为原点,建立空 间直角坐标系,如图所示,
在等腰梯形中 ,AD//BC,AB=BC=CD=1,AD=2,
则 ,
所以 , ,
设平面 的法向量为 ,因为 ,
所以 ,令 ,则 ,
设平面 的法向量为 ,因为 ,
所以 ,令 ,则 ,
所以 .
20、
【答 案】
(1)
(2)
【分析】
(1)根据短轴长为 , 可求出 , ,再根据椭圆定义可求出 ,得到椭圆方程;
(2)直线 , 关于直线 对称,转化成 ,代入韦达定理求出 过定点
, ,再求 的面积的最大值.
【详解】
(1)(1)由题意可得
故 , , = + =3,故椭圆 的方程为 ;
(2)设 , , , ,
由 知 , ,所以直线 过点 ,因为两条不重合的直线 , 关于直线 对称,所以
, ,且 , 不同时为 的左,右顶点,设直线 的方程为 ,由
,得 ,则 , , 因为
直线 , 关于直线 对称
所以 ,则
,
所以 ,
即 , 因为 ,所以 ,
所以直线 恒过定点 , ,且 ,
当 与 的上顶点或下顶点重合,即 时, 的面积的最大,
即最大值为 .
21、
【答案 】
(1)递增区间为 ,递减区间为
(2) .
【分析】
(1)由导数得出函数 的单调区间;
(2)设 ,由导数得出 ,再由
得出 ,最后由导数解不等式 得出正实数 的取值范围.
【详解】
(1)函数 的定义域为 ,
当 或 时, , 单调递增;
当 时, , 单调递减,
故函数 的单调递增区间为
函数 的单调递减区间为 .
(2)原题等价于对任意 ,有 恒成立,
设 , ,所以
,令 ,得 ;令 ,得 ,
所以函数 在 , 上单调递减,在 上单调递增
设
则
所以 在 , 上单调递增,故 ,所以 ,
从而 , 所以 ,即 ,
设 ,则 ,
所以 在 , 上单调递增,
又 ,所以 的解为 ,
因为 ,所以正实数 的取值范围为 , .
【点睛】
关键点睛: 在问题二中,关键是将不等式的恒成立问题,转化为 ,再解不等式
得出正实数 的取值范围.
22、
【答案 】
(1) , ;
(2) .
【分析】
(1)消去 t 可得直线在直角坐标系的方程,运用极坐标与直角坐标的关系,可得曲线C的直角坐标方程;
(2)理解参数方程中 t 的意义,联立C与直线方程,应用韦达定理即可.
【详解】
(1)对于直线 ,消去 t 得 ;
由于 ,曲线C的方程为 ,
所以 ,即 ;
(2)联立方程 ,得 ,
设 和 对应的参数为 和 ,
由韦达定理 ,以及 t 的几何意义得:
= = = .
23、
【答 案】
(1) 或 ;(2) .
【分析】
(1)分类讨论 , 和 三种情况,求解 ,最后求并集即可;(2)根据(1)可
得 ,可得 ,利用柯西不等式求出 的最小值即可.
【详解】
(1)当 时, ,解得 ;
当 时, ,解得 ;
当 时, ,解得 .
综上,不等式 的解集为 或 .
(2)由(1)可知当 时, ,即 ,则 .
因为 ,
所以 ,即 (当且仅当 时等号成立).
故 的最小值为 .
【点睛】
方法点睛 :绝对值不等式的解法一般有:
法一:利用绝对值不等式的几何意义求解 ,体现了数形结合的思想;
法二:利用“零点分段法”求解,体现了分类讨论的思想;
法三:通过构造函数,利用函数的图象求解,体现了函数 与方程的思想.
同课章节目录
