2022~2023学年青海玉树高二下学期期末理科数学试卷(三校(二高、三高、五高))(PDF版含解析)
文档属性
| 名称 | 2022~2023学年青海玉树高二下学期期末理科数学试卷(三校(二高、三高、五高))(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 19:59:37 | ||
图片预览

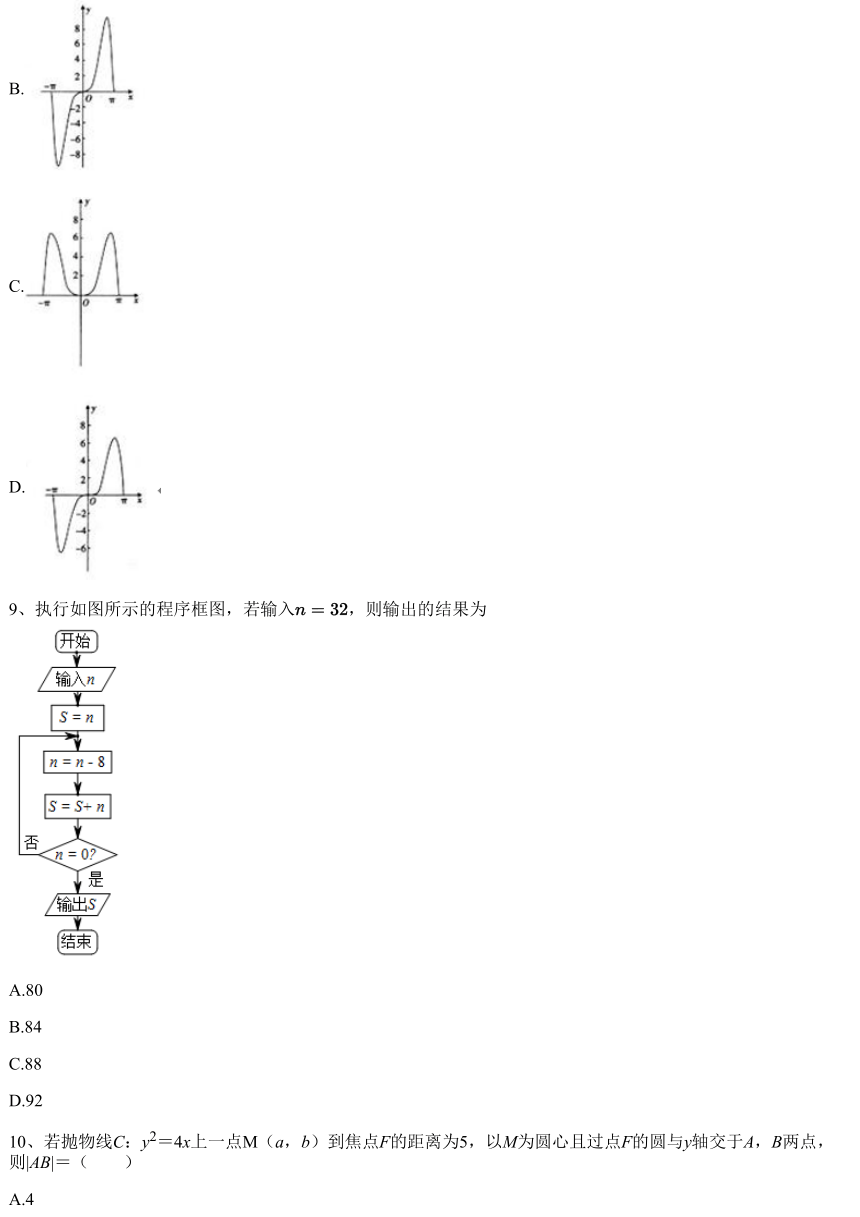

文档简介
2022~2023学年青海玉树高二下学期期末理科数学试卷(三校(二高、三
高、五高))
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 ,则
A.
B. 或
C.
D. 或
2、若 i i i,其中 ,则 ( )
A.3
B.2
C.-2
D.-3
3、已知向量 , ,且 ,则 ( )
A.
B.
C.
D.
4、 的展开式中常数项为( )
A.
B.5
C.10
D.
5、若双曲线 的一条渐近线与直线 垂直,则该双曲线的离心率为
( )
A.2
B.
C.
D.
6、已知等比数列 的前 项和为 ,若 , ,则 ( ).
A.
B.
C.
D.
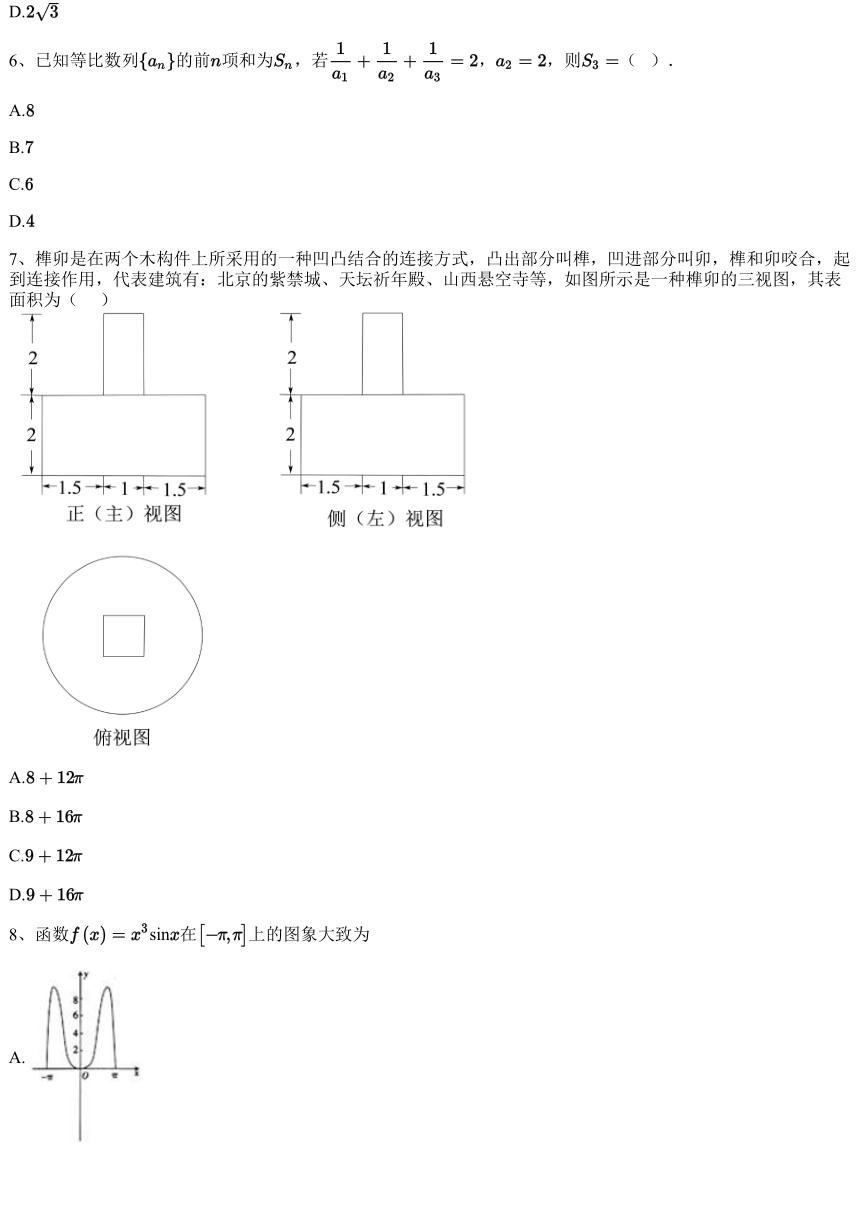
7、榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,凸出部分叫榫,凹进部分叫卯,榫和卯咬合,起
到连接作用,代表建筑有:北京的紫禁城、天坛祈年殿、山西悬空寺等,如图所示是一种榫卯的三视图,其表
面积为( )
A.
B.
C.
D.
8、函数 sin 在 上的图象大致为
A.
B.
C.
D.
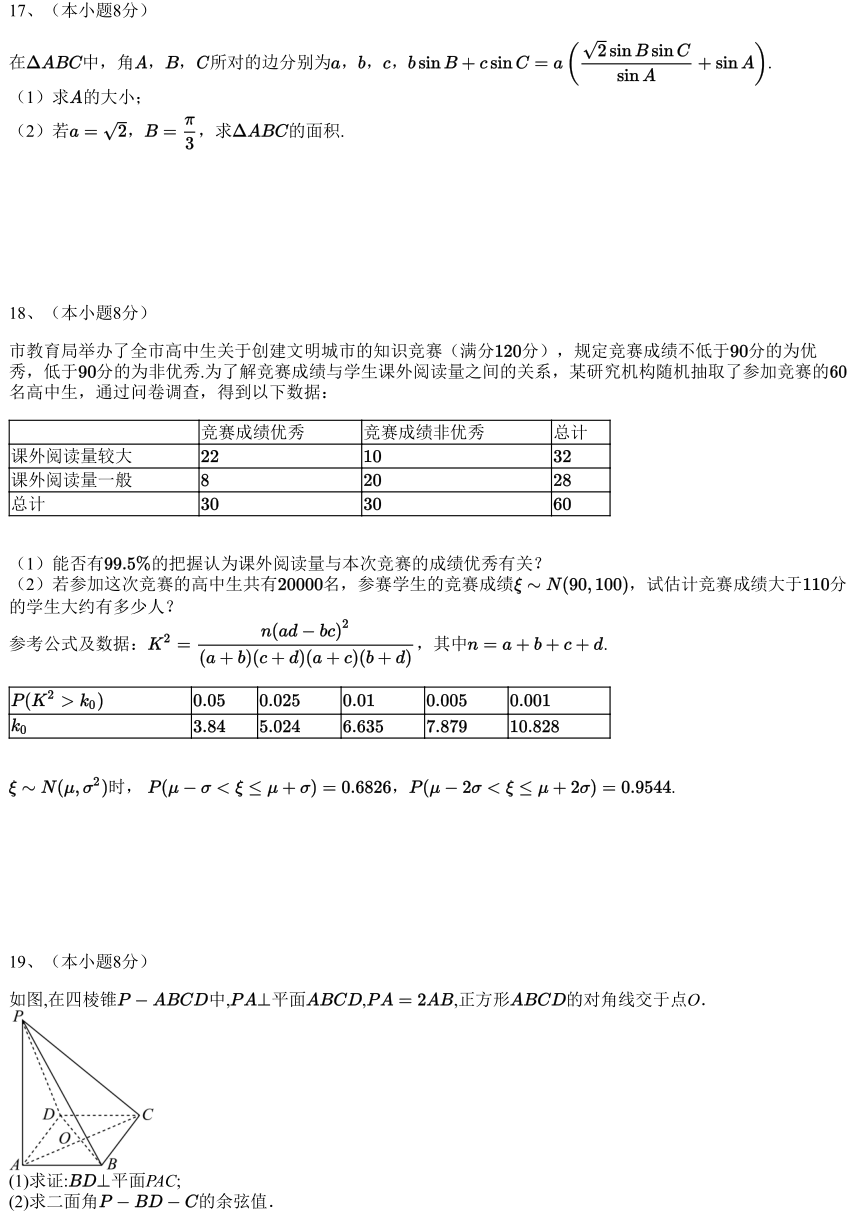
9、执行如图所示的程序框图,若输入 ,则输出的结果为
A.80
B.84
C.88
D.92
10、若抛物线C:y2=4x上一点M(a,b)到焦点F的距离为5,以M为圆心且过点F的圆与y轴交于A,B两点,
则|AB|=( )
A.4
B.6
C.
D.8
11、如图为函数 的部分图像,将 的图像上各点的横坐标变为原来的两倍,再
向左平移 个单位长度,得到函数 的图像,则 ( ).
A.
B.
C.
D.
ln ln
12、设 , , ,则
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知 之间具有线性相关关系,若通过10组数据 得到的回归方程为
,且 ,则 .
14、函数 的图象在点 处的切线方程为 .
15、已知f(x)是R上以3为周期的奇函数,则有以下结论:
① ;
② ;
③ 的图像关于点 对称;
④
其中所有正确结论的序号是 .
16、在四面体 中, 底面 , , , 为棱 的中点,点 在 上且满
足 ,若四面体 的外接球的表面积为 ,则 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
在 中,角 , , 所对的边分别为 , , , .
(1)求 的大小;
(2)若 , ,求 的面积.
18、(本小题8分)
市教育局举办了全市高中生关于创建文明城市的知识竞赛(满分 分),规定竞赛成绩不低于 分的为优
秀,低于 分的为非优秀.为了解竞赛成绩与学生课外阅读量之间的关系,某研究机构随机抽取了参加竞赛的
名高中生,通过问卷调查,得到以下数据:
竞赛成绩优秀 竞赛成绩非优秀 总计
课外阅读量较大
课外阅读量一般
总计
(1)能否有 的把握认为课外阅读量与本次竞赛的成绩优秀有关?
(2)若参加这次竞赛的高中生共有 名,参赛学生的竞赛成绩 ,试估计竞赛成绩大于 分
的学生大约有多少人?
参考公式及数据: ,其中 .
时, , .
19、(本小题8分)
如图,在四棱锥 中, 平面 , ,正方形 的对角线交于点O.
(1)求证: 平面PAC;
(2)求二面角 的余弦值.
20、(本小题10分)
已知点 为椭圆 ( )上任一点,椭圆的一个焦点坐标为 .
(1)求椭圆的标准方程;
(2)若点 是抛物线 的准线上的任意一点,以 为直径的圆过原点 ,试判断
是否为定值?若是,求出这个定值;若不是,请说明理由.
21、(本小题12分)
已知 e .
(1)若 ,求 的单调区间与 极值;
(2)若关于 的方程 在 上有两个不同的实数根,求实数 的取值范围.
e
参考数据:
22、(本小题12分)
在直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点. 轴的正半轴为极轴
建立极坐标系,曲线 的极坐标方程为 .
(1)求 和 的直角坐标方程;
(2)若 与 恰有4个公共点,求 的取值范围.
23、(本小题12分)
设函数 .
(1)当 时,求不等式 的解集;
(2)若 ,求 的取值范围.
参考答案
一、单选题
1、
【答 案】
D
【分析】
因为 ,所以 或 .
因此正确答案为D
2、
【答 案】
D
【分析】
∵
∴ 解得
因此正确答案为:D.
3、
【答 案】
A
【分析】
因为 ,所以 ,解得 ,则 .
因此正确答案为:A
4、
【答 案】
C
【分析】
由题得二项式展开式的通项为 ,
令 .
所以所求常数项为 C .
因此正确答案为:C.
5、
【答 案】
C
【分析】
∵双曲线 的一条渐近线与直线 垂直.
∴双曲线的渐近线方程为 ,
∴ ,得 , ,
此时,离心率 .
因此正确答案为C.
6、
【答 案】
A
【分析】
已知 为等比数列,
,
, ,则 .
故选A.
7、
【答 案】
B
【分析】
由三视图可知该几何体由底边长为 、高为 正四棱柱和底面半径为 、高为 的圆柱体组合而成
侧面积为 ,上下底面积的和为 ,则其表面积
,
因此正确答案为:B.
8、
【答 案】
A
【分析】
∵ ,∴ 为偶函数,排除B,D.
∵ ,∴排除C,
因此正确答案为A.
9、
【答 案】
A
【分析】
由题设可知当 时, ,程序运算继续执行 ,
程序运算继续执行 ,程序运算继续执行 ,故此时运算程序
结束,输出 ,应选答案A.
10、
【答案 】
B
【分析】
抛物线C:y2=4x的焦点为(1,0),准线方程为x=﹣1,
由抛物线的定义可得a+1=5,解得a=4,b=±4,
以M(4,±4)为圆心且过点F的圆的半径为 5,
由圆心到y轴的距离为4,可得|AB|=2 6,
因此正确答案为B.
11、
【答 案】
D
【分析】
根据函数 的部分图像,
可得 ,
∴ ,
再根据五点法作图,可得 , ,
∴ , ,取 ,
∴ .
将函数 的图像上各点的横坐标变为原来的两倍,
可得 的图像;再向左平移 个单位长度,
得到函数 的图像,
故选D.
12、
【答案 】
C
【分析】
ln ln ln
, , ,
ln ln
令 ,得 ,
当 时, 为增函数,当 时, 为减函数,
ln ln
则 最大,而 ln , ln ,
,
.
因此正确答案为 C.
二、填空题
13、
【答案 】
8
【分析】
通过题意知, ,因为回归方程为 ,
所以可以计算出 ,所以
因此正确答案为:8
14、
【答案 】
【分析】
因为 ,
所以 ,又 ,所 以切线斜率为 ,切点坐标为
故切线方程为 ,即 .
因此正确答案为:
15、
【答案 】
①③④
【分析】
由 是 上的奇函数得: ,
又f(x)是以3为周期的周期函数,则 ,①无误;
,②有误;
由 得: ,即 ,即 的图像
关于点 对称,③无误;
由 可得 ,于是得 ,④无误,
所以给出的4个命题正确的是①③④.
因此正确答案为:①③④
16、
【答案 】
2
【分析】
解:
通过题意可得,点G是△ABC的重心,
AG= AE= =2,
设△ABC的外心为O,通过题意可得点O在AE上,
令OA=r,则OE + EC =OC ,即 r + = ,解得 ,
AD⊥平面ABC,
四面体ABCD的外接球的半径 ,
解得AD=4,
tan∠AGD= =2
故答案:2.
三、解答题
17、
【答案 】
(1) .(2)
【分析】
(1)因为 ,
由正弦定理可得: ,
即 ,
再由余弦定理可得 ,即 ,
所以 ;
(2)因为 ,所以 ,
由正弦定理 ,可得 .
.
18、
【答案 】
(1)有 的把握认为课外阅读量与本次竞赛的成绩优秀有关;(2) 人.
【分析】
(1)∵ ,
∴有 的把握认为课外阅读量与本次竞赛的成绩优秀有关.
(2)由 ,知: , .
∴ ,故竞赛成绩大于 分的学生约
有 ,
∴估计竞赛成绩大于 分的 学生大约有 人.
19、
【答 案】
(1)证明见解析;
(2)
【分析】
(1)解:通过题意分析可以得 平面 ,
,
正方形 ,
,
平面 , 平面 ,
平面 .
(2)通过题意分析 可以得 平面 , 为正方形,
以 为坐标原点, 方向为 轴, 方向为 轴, 方向为 轴 建立空间直角坐标系如下图所示:
不妨设 , ,
,
,
记平面 法向量为 ,
,
即 ,
不妨取 ,则 ,
平面 ,
平面 法向量为 ,
,
由图象可以知二面角 的大小为钝角,
故二面角 的余弦值为 .
20、
【答 案】
(1) ;(2) 为定值,且定值为1.
【分析】
解:(1)因为椭圆 的一个焦点坐标为 ,
所以 ,
所以 ,所以 ,
因为 ,所以 .
所以椭圆 的标准方程为 ;
(2)由(1)知抛物线 的标准方程为 ,其准线方程为: ,
设 , ,
因为以 为直径的圆过原点,所以 ,所以 ,
所以 ,即 ,
所以 ,
又因为 , ,
所以 ,
所以 为定值,且定值为1.
21、
【答 案】
(1)答案见解析
(2)
【分析】
(1)解:当 时, e ,该函数的定义域为 ,
e e ,列表如下:
增
极大值
减
极小值
增
所以,函数 的增区间为 、 ,减区间为 ,
极大值为 ,即小值为 e .
e
(2)解:通过题意可知,关于 的方程 在 上有两个不同的实数根,
即关于 的方程 在 上有两个不同的实数根,
令 ,其中 ,则 ,
由 可得 ;由 可得 .
所以,函数 在 上单调递增,在 上单调递减.
所以, ,
又因为 , ,
因为 ,则 ,
作出函数 与函数 在 上的图象如下图所示:
由图象可以知,当 时,直线 与函数 在 上的图象有两个交点.
因此,实数 的取值范围是 .
22、
【答案 】
(1) , ;(2)
【分析】
(1)曲线 的参数方程为 ( 为参数),
则 ,得 ,
故 的直角坐标方程为 ;
由 , 得 ,
. 故 的直角坐标方程为
(2)因为 与 恰有4个公共点,则 ,
当 和 相切时,此时 与 恰有2个公共 点,
圆 的圆心到直线 的距离 ,解得 ;
当 与 恰有3个公共点时,此时圆 过点 ,解得 ;
故当 与 恰有4个公共点时, 的取值范围为 .
23、
【答 案】
(1) ;(2)
【分析】
(1)当 时, ,
故不等式 的解集为 ;
(2) ,
,
则 或 ,
解得 或 ,
故 的取值范围为 .
高、五高))
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 ,则
A.
B. 或
C.
D. 或
2、若 i i i,其中 ,则 ( )
A.3
B.2
C.-2
D.-3
3、已知向量 , ,且 ,则 ( )
A.
B.
C.
D.
4、 的展开式中常数项为( )
A.
B.5
C.10
D.
5、若双曲线 的一条渐近线与直线 垂直,则该双曲线的离心率为
( )
A.2
B.
C.
D.
6、已知等比数列 的前 项和为 ,若 , ,则 ( ).
A.
B.
C.
D.
7、榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,凸出部分叫榫,凹进部分叫卯,榫和卯咬合,起
到连接作用,代表建筑有:北京的紫禁城、天坛祈年殿、山西悬空寺等,如图所示是一种榫卯的三视图,其表
面积为( )
A.
B.
C.
D.
8、函数 sin 在 上的图象大致为
A.
B.
C.
D.
9、执行如图所示的程序框图,若输入 ,则输出的结果为
A.80
B.84
C.88
D.92
10、若抛物线C:y2=4x上一点M(a,b)到焦点F的距离为5,以M为圆心且过点F的圆与y轴交于A,B两点,
则|AB|=( )
A.4
B.6
C.
D.8
11、如图为函数 的部分图像,将 的图像上各点的横坐标变为原来的两倍,再
向左平移 个单位长度,得到函数 的图像,则 ( ).
A.
B.
C.
D.
ln ln
12、设 , , ,则
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知 之间具有线性相关关系,若通过10组数据 得到的回归方程为
,且 ,则 .
14、函数 的图象在点 处的切线方程为 .
15、已知f(x)是R上以3为周期的奇函数,则有以下结论:
① ;
② ;
③ 的图像关于点 对称;
④
其中所有正确结论的序号是 .
16、在四面体 中, 底面 , , , 为棱 的中点,点 在 上且满
足 ,若四面体 的外接球的表面积为 ,则 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
在 中,角 , , 所对的边分别为 , , , .
(1)求 的大小;
(2)若 , ,求 的面积.
18、(本小题8分)
市教育局举办了全市高中生关于创建文明城市的知识竞赛(满分 分),规定竞赛成绩不低于 分的为优
秀,低于 分的为非优秀.为了解竞赛成绩与学生课外阅读量之间的关系,某研究机构随机抽取了参加竞赛的
名高中生,通过问卷调查,得到以下数据:
竞赛成绩优秀 竞赛成绩非优秀 总计
课外阅读量较大
课外阅读量一般
总计
(1)能否有 的把握认为课外阅读量与本次竞赛的成绩优秀有关?
(2)若参加这次竞赛的高中生共有 名,参赛学生的竞赛成绩 ,试估计竞赛成绩大于 分
的学生大约有多少人?
参考公式及数据: ,其中 .
时, , .
19、(本小题8分)
如图,在四棱锥 中, 平面 , ,正方形 的对角线交于点O.
(1)求证: 平面PAC;
(2)求二面角 的余弦值.
20、(本小题10分)
已知点 为椭圆 ( )上任一点,椭圆的一个焦点坐标为 .
(1)求椭圆的标准方程;
(2)若点 是抛物线 的准线上的任意一点,以 为直径的圆过原点 ,试判断
是否为定值?若是,求出这个定值;若不是,请说明理由.
21、(本小题12分)
已知 e .
(1)若 ,求 的单调区间与 极值;
(2)若关于 的方程 在 上有两个不同的实数根,求实数 的取值范围.
e
参考数据:
22、(本小题12分)
在直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点. 轴的正半轴为极轴
建立极坐标系,曲线 的极坐标方程为 .
(1)求 和 的直角坐标方程;
(2)若 与 恰有4个公共点,求 的取值范围.
23、(本小题12分)
设函数 .
(1)当 时,求不等式 的解集;
(2)若 ,求 的取值范围.
参考答案
一、单选题
1、
【答 案】
D
【分析】
因为 ,所以 或 .
因此正确答案为D
2、
【答 案】
D
【分析】
∵
∴ 解得
因此正确答案为:D.
3、
【答 案】
A
【分析】
因为 ,所以 ,解得 ,则 .
因此正确答案为:A
4、
【答 案】
C
【分析】
由题得二项式展开式的通项为 ,
令 .
所以所求常数项为 C .
因此正确答案为:C.
5、
【答 案】
C
【分析】
∵双曲线 的一条渐近线与直线 垂直.
∴双曲线的渐近线方程为 ,
∴ ,得 , ,
此时,离心率 .
因此正确答案为C.
6、
【答 案】
A
【分析】
已知 为等比数列,
,
, ,则 .
故选A.
7、
【答 案】
B
【分析】
由三视图可知该几何体由底边长为 、高为 正四棱柱和底面半径为 、高为 的圆柱体组合而成
侧面积为 ,上下底面积的和为 ,则其表面积
,
因此正确答案为:B.
8、
【答 案】
A
【分析】
∵ ,∴ 为偶函数,排除B,D.
∵ ,∴排除C,
因此正确答案为A.
9、
【答 案】
A
【分析】
由题设可知当 时, ,程序运算继续执行 ,
程序运算继续执行 ,程序运算继续执行 ,故此时运算程序
结束,输出 ,应选答案A.
10、
【答案 】
B
【分析】
抛物线C:y2=4x的焦点为(1,0),准线方程为x=﹣1,
由抛物线的定义可得a+1=5,解得a=4,b=±4,
以M(4,±4)为圆心且过点F的圆的半径为 5,
由圆心到y轴的距离为4,可得|AB|=2 6,
因此正确答案为B.
11、
【答 案】
D
【分析】
根据函数 的部分图像,
可得 ,
∴ ,
再根据五点法作图,可得 , ,
∴ , ,取 ,
∴ .
将函数 的图像上各点的横坐标变为原来的两倍,
可得 的图像;再向左平移 个单位长度,
得到函数 的图像,
故选D.
12、
【答案 】
C
【分析】
ln ln ln
, , ,
ln ln
令 ,得 ,
当 时, 为增函数,当 时, 为减函数,
ln ln
则 最大,而 ln , ln ,
,
.
因此正确答案为 C.
二、填空题
13、
【答案 】
8
【分析】
通过题意知, ,因为回归方程为 ,
所以可以计算出 ,所以
因此正确答案为:8
14、
【答案 】
【分析】
因为 ,
所以 ,又 ,所 以切线斜率为 ,切点坐标为
故切线方程为 ,即 .
因此正确答案为:
15、
【答案 】
①③④
【分析】
由 是 上的奇函数得: ,
又f(x)是以3为周期的周期函数,则 ,①无误;
,②有误;
由 得: ,即 ,即 的图像
关于点 对称,③无误;
由 可得 ,于是得 ,④无误,
所以给出的4个命题正确的是①③④.
因此正确答案为:①③④
16、
【答案 】
2
【分析】
解:
通过题意可得,点G是△ABC的重心,
AG= AE= =2,
设△ABC的外心为O,通过题意可得点O在AE上,
令OA=r,则OE + EC =OC ,即 r + = ,解得 ,
AD⊥平面ABC,
四面体ABCD的外接球的半径 ,
解得AD=4,
tan∠AGD= =2
故答案:2.
三、解答题
17、
【答案 】
(1) .(2)
【分析】
(1)因为 ,
由正弦定理可得: ,
即 ,
再由余弦定理可得 ,即 ,
所以 ;
(2)因为 ,所以 ,
由正弦定理 ,可得 .
.
18、
【答案 】
(1)有 的把握认为课外阅读量与本次竞赛的成绩优秀有关;(2) 人.
【分析】
(1)∵ ,
∴有 的把握认为课外阅读量与本次竞赛的成绩优秀有关.
(2)由 ,知: , .
∴ ,故竞赛成绩大于 分的学生约
有 ,
∴估计竞赛成绩大于 分的 学生大约有 人.
19、
【答 案】
(1)证明见解析;
(2)
【分析】
(1)解:通过题意分析可以得 平面 ,
,
正方形 ,
,
平面 , 平面 ,
平面 .
(2)通过题意分析 可以得 平面 , 为正方形,
以 为坐标原点, 方向为 轴, 方向为 轴, 方向为 轴 建立空间直角坐标系如下图所示:
不妨设 , ,
,
,
记平面 法向量为 ,
,
即 ,
不妨取 ,则 ,
平面 ,
平面 法向量为 ,
,
由图象可以知二面角 的大小为钝角,
故二面角 的余弦值为 .
20、
【答 案】
(1) ;(2) 为定值,且定值为1.
【分析】
解:(1)因为椭圆 的一个焦点坐标为 ,
所以 ,
所以 ,所以 ,
因为 ,所以 .
所以椭圆 的标准方程为 ;
(2)由(1)知抛物线 的标准方程为 ,其准线方程为: ,
设 , ,
因为以 为直径的圆过原点,所以 ,所以 ,
所以 ,即 ,
所以 ,
又因为 , ,
所以 ,
所以 为定值,且定值为1.
21、
【答 案】
(1)答案见解析
(2)
【分析】
(1)解:当 时, e ,该函数的定义域为 ,
e e ,列表如下:
增
极大值
减
极小值
增
所以,函数 的增区间为 、 ,减区间为 ,
极大值为 ,即小值为 e .
e
(2)解:通过题意可知,关于 的方程 在 上有两个不同的实数根,
即关于 的方程 在 上有两个不同的实数根,
令 ,其中 ,则 ,
由 可得 ;由 可得 .
所以,函数 在 上单调递增,在 上单调递减.
所以, ,
又因为 , ,
因为 ,则 ,
作出函数 与函数 在 上的图象如下图所示:
由图象可以知,当 时,直线 与函数 在 上的图象有两个交点.
因此,实数 的取值范围是 .
22、
【答案 】
(1) , ;(2)
【分析】
(1)曲线 的参数方程为 ( 为参数),
则 ,得 ,
故 的直角坐标方程为 ;
由 , 得 ,
. 故 的直角坐标方程为
(2)因为 与 恰有4个公共点,则 ,
当 和 相切时,此时 与 恰有2个公共 点,
圆 的圆心到直线 的距离 ,解得 ;
当 与 恰有3个公共点时,此时圆 过点 ,解得 ;
故当 与 恰有4个公共点时, 的取值范围为 .
23、
【答 案】
(1) ;(2)
【分析】
(1)当 时, ,
故不等式 的解集为 ;
(2) ,
,
则 或 ,
解得 或 ,
故 的取值范围为 .
同课章节目录
