2022~2023学年陕西西安碑林区西安市铁一中学高三上学期期末理科数学试卷(1月)(图片版,含解析)
文档属性
| 名称 | 2022~2023学年陕西西安碑林区西安市铁一中学高三上学期期末理科数学试卷(1月)(图片版,含解析) |

|
|
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 10:51:07 | ||
图片预览



文档简介
2022~2023学年陕西西安碑林区西安市铁一中学高三上学期期末理科数学
试卷(1月)
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则 ( )
A.
B.
C.
D.
2、已知复数 满足 ,则在复平面内与复数 对应的点的坐标为( )
A.
B.
C.
D.
3、下列函数在区间 上是增函数的是
A.
B. log
C.
D.
4、已知椭圆 的左右焦点分别为 , ,若椭圆上存在点 ,使
,则该椭圆离心率的取值范围为( )
A.
B.
C.
D.
5、下列函数中同时具有以下性质的是( )
①最小正周期是 ; ②图象关于直线 对称;
③在 上是增函数; ④图象的一个对称中心为 .
A.
B.
C.
D.
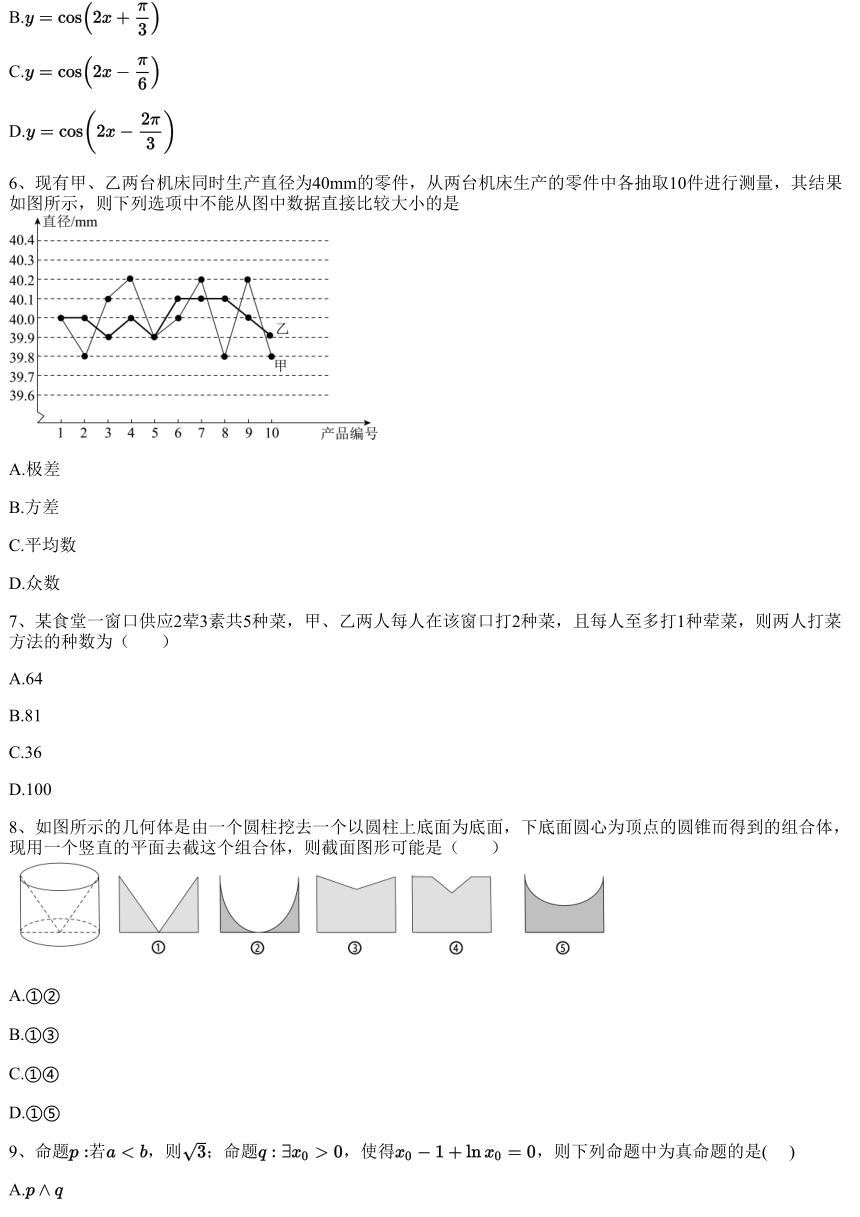
6、现有甲、乙两台机床同时生产直径为40mm的零件,从两台机床生产的零件中各抽取10件进行测量,其结果
如图所示,则下列选项中不能从图中数据直接比较大小的是
A.极差
B.方差
C.平均数
D.众数
7、某食堂一窗口供应2荤3素共5种菜,甲、乙两人每人在该窗口打2种菜,且每人至多打1种荤菜,则两人打菜
方法的种数为( )
A.64
B.81
C.36
D.100
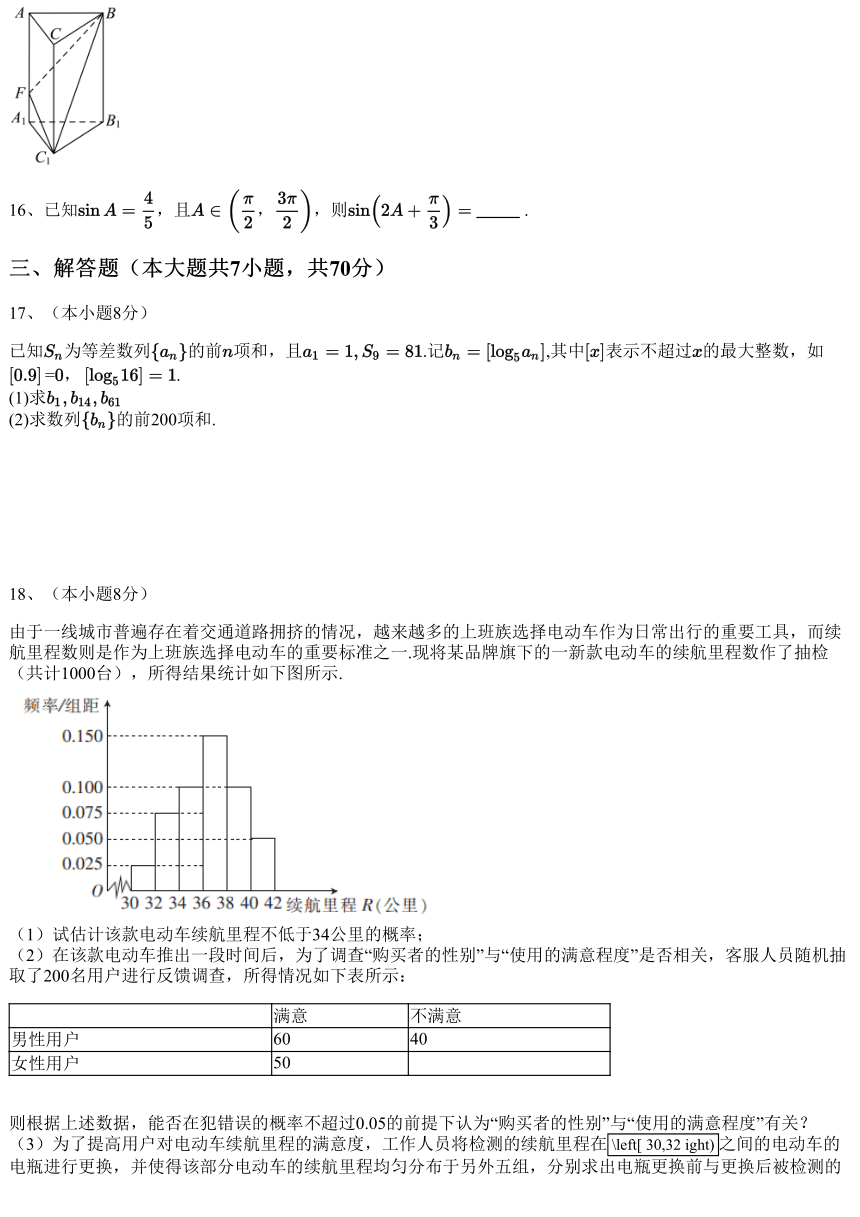
8、如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,
现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①②
B.①③
C.①④
D.①⑤
9、命题 若 ,则 ;命题 ,使得 ,则下列命题中为真命题的是( )
A.
B.
C.
D.
10、体积为1的正方体的内切球的体积是( )
A.
B.
C.
D.
11、已知函数 ,若 .且 ,则 的取值范围是( )
A.
B.
C.
D.
12、已知函数 .若 恰有4个零点,则实数 的取值范围是
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知双曲线 的渐近线方程为 ,则 .
14、已知向量 ,则 在 上的投影向量的坐标为 .
15、如图,在直三棱柱ABC-A1B1C1中, , , , ,F为棱AA1上的一动点,则
当BF+FC1最小时,△BFC1的面积为 .
16、已知 ,且 , ,则 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知 为等差数列 的前 项和,且 .记 ,其中 表示不超过 的最大整数,如
= , .
(1)求
(2)求数列 的 前200项和.
18、(本小题8分)
由于一线城市普遍存在着交通道路拥挤的情况,越来越多的上班族选择电动车作为日常出行的重要工具,而续
航里程数则是作为上班族选择电动车的重要标准之一.现将某品牌旗下的一新款电动车的续航里程数作了抽检
(共计1000台),所得结果统计如下图所示.
(1)试估计该款电动车续航里程不低于34公里的概率;
(2)在该款电动车推出一段时间后,为了调查“购买者的 性别”与“使用的满意程度”是否相关,客服人员随机抽
取了200名用户进行反馈调查,所得情况如下表所示:
满意 不满意
男性用户 60 40
女性用户 50
则根据上述数据,能否在犯错误的概率不超过0.05的前提下认为“购买者的性别”与“使用的满意程度”有关?
(3)为了提高用户对电动车续航里程的满意度,工作人员将检测的续航里程在 \left[ 30,32 ight) 之间的电动车 的
电瓶进行更换,并使得该部分电动车的续航里程均匀分布于另外五组,分别求出电瓶更换前与更换后被检测的
电动车的平均续航里程,并计算更换后比更换前的平均续航里程多了多少.
附参考公式: {{K}^{2}}=\frac{n{{\left( ad-bc ight)}^{2}}}{\left( a+b ight)\left( c+d ight)\left( a+c ight)\left( b+d ight)} .
P\left( {{K}^{2}}\ge k ight) 0.100 0.050 0.010 0.001
2.706 3.841 6.635 10.828
19、(本小题8分)
如图,在棱长为2的正方体 中,E为 的中点.
(1)求证: 平面 ;
(2)求平面 与平面 夹角的余弦值.
20、(本小题10分)
已知抛物线 截直线 所得弦长 .
(1)求m的值;
(2)设P是x轴上 的点,且 的面积为9,求点P的坐标.
21、(本小题12分)
已知函数
(1)当 时,求函数 的单调区间;
(2)若 恒成立,求 的最小值.
22、(本小题12分)
以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ﹣ ,直
线l的极坐标方程为 ( ).
(1)求曲线C的参数方程,若曲线C过原点O,求实数a的值;
(2)当 时,直线l与曲线C交于A,B两点,求 .
23、(本小题12分)
设函数 .
(1)当 时,求不等式 的解集;
(2)若关于x的不等式 有解,求实数a的取值 范围.
参考答案
一、单选题
1、
【答 案】
B
【分析】
由 ,则 ,即 ,由 ,则 ,
因此正确答案为:B.
2、
【答 案】
B
【分析】
,
复数 对应的点的坐标为 .
因此正确答案为:B.
3、
【答 案】
B
【分析】
A.函数y=4﹣5x在R上单调递减,为减函数.
B.函数y=log 3x+1在(0,+∞)上单调递增,∴在区间(0,2)上是增函数,正确.
C.函数y=x2﹣2x+3的对称轴为x=1,∴函数在(﹣∞,1)上单调递减,在(1,+∞)上单调递增,∴C有误.
D .函数y=﹣2x,在R上单调递减,为减函数.
因此正确答案为B.
4、
【答 案】
C
【分析】
由椭圆的定义知: ,
因为 ,即 ,
又因为 ,所以 ,
所以有: ,
,
故椭圆的离心率的取值范围是 .
因此正确答案为:C
5、
【答 案】
D
【分析】
对A:函数的最小正周期为 ,故A不正确;
对B:该函数在区间 为减函数,故B不正确;
对C:函数图像不关于 直线对称,故C不正确;
对D:该函数满足四条性质,故D正确.
因此正确答案为:D.
6、
【答 案】
C
【分析】
由于极差反映所有数据中最大值与最小值的差的大小,
方差反映所有数据的波动大小,
平均数反映所有数据的平均值的 大小,
众数反映所有数据中出现次数最多的数的 大小,
因此由图象可以知不能从图中数据直接比较平均 数的大小.
因此正确答案为:C
7、
【答 案】
B
【分析】
甲有两种情况:一荤一素, 种;两素, 种.故甲共有 种,同理乙也有9种,则两人打菜
方法的种数为 种.因此正确答案为B.
8、
【答 案】
D
【分析】
一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是矩形除去一条边,
当截面经过圆柱上下底面的圆心时,圆锥的截面为三角形除去一条边,所以①无误;
当截面不经过圆柱上下底面的圆心时,圆锥的截面为抛物线的一部分,所以⑤正确;
因此正确答案为:D
9、
【答 案】
C
【分析】
若 ,则 ,在 时不成立,故 是假命题;
,使得 ln ,故命题 为真命题,
故命题 , , 是假命题,命题 是真命题.
因此正确答案为:C
10、
【答案 】
A
【分析】
如下图所示,因为正方体的体积为1,所以其边长为1
其内切球的球心为正方体的中心 ,半径为
则球的体积为 .
因此正确答案为:A
11、
【答 案】
B
【分析】
的图象如下:
因为 .且
所以 且
所以 ,所以
所以
当且仅当 ,即 时等号成立
因此正确答案为:B
12、
【答 案】
A
【分析】
恰有4个零点等价于方程 有四个不同的根,
等价于y 的图象有四个不同的交点,
作出y 的图象,
由图象可以知 时,两图象有三个 交点,
由 ,由 ,
此时 过y h x ln 上的点 ,h x ,
所以h ,即 与y ln 相切,
可得 时,两图象有两个交点,
由图象可以知,当 时,y 的图象有四个不同的交点,
即 恰有4个零点,
所以,若 恰有4个 零点,则实数 的取值范围是 ,因此正确答案为A.
二、填空题
13、
【答案 】
【分析】
当 时,双曲线 的渐近线方程为 ,
通过题意得 ,解得 .
因此正确答案为 .
14、
【答案 】
【分析】
利用向量的投影向量公式,代入坐标进行计算即可.
【详解】
解:向量 , ,
在 上的投影向量的坐标为: , .
故答案为: , .
15、
【答案 】
【分析】
解:通过题意得
将直三棱柱 的侧面沿 剪开,并展开到同一平面上,如下图所示:
连接 ,则 与 的交点即为 最小时的点 .
在展开图中, , , .
又由 易知,
由此可知
在直三棱柱 中,
在 中,
故△BFC1的面积为
因此正确答案为:
16、
【答案 】
【分析】
因为 ,且 , ,所以 ,
则 ,
,
因此 .
因此正确答案为: .
三、解答题
17、
【答案 】
(1) ; ;
(2)524
【分析】
(1)设等差数列 的公差为d,
由已知 = ,根据等差数列性质可知:
∴ . ∵ ,所以
∴
∴ log , log , log .
(2 )当 时, , log ,共2项;
当 时, log ,共10项;
当 时, log ,共50项;
当 时, log ,共138 项.
∴ 数列 的前200项和为 .
18、
【答案 】
(1)0.8;(2)表格见解析,不能;(3)36.5(公里),36.8(公里),更换后比更换前的平均续航里程多了
0.3公里.
【分析】
解:(1)由频率分布直方图可知该款电动车续航里程不低于34公里的频率为
,故该款电动车续航里程不低于34公里的概率的
估计值为0.8.
(2)通过题 意,得到 列联表如下:
满意 不满意 总计
男性用户 60 40 100
女性用户 50 50 100
总计 110 90 200
则 的观测值
k=\frac{200 imes {{\left( 60 imes 50-40 imes 50 ight)}^{2}}}{100 imes 100 imes 110 imes 90}=\frac{200}{99}\approx 2.020< 3.841
,故不能在犯错误的概率不超过0.05的前提下认为“购买者的性别”与“使用的满意程度”有关;
(3)通过题意,电瓶更换前被检测电动车的平均续航里程为
(公里)
电瓶更换后被检 测电动车的平均续航里程为
(公里)
故更换后比更换 前的平均续航里程多了0.3公里.
19、
【答 案】
(1)证明见解析
(2)
【分析】
(1)证明:由正方体的性质可知, ,且 ,
所以四边形 是平行四边形,
所以 .
因为 平面 , 平面 ,
所以 平面 .
(2)以A为原点, 、 、 分别为x轴、y轴、z轴,建立如下图所示的空间直角坐标系.
则 ,
所以 , , ,
设平面 的法向量为 ,
则 ,令 ,则 , , ,
易知平面 的一个法向量为 , ,
所以 ,
所以平面 与平面 夹角的余弦值为 .
20、
【答案 】
(1) ;(2) 或 .
【分析】
(1)设 .
由 ,得 ,
,
由根与系数的关系得 .
∴
,
∵ ,∴ ,
解得 .
(2)由(1) 知直线 的方程为 .
设 ,点P到直线 的距离为d,
则 .
又 ,则 ,
∴ ,
∴ ,
∴ 或 .
故点P的坐标为 或 .
21、
【答 案】
(1) 单调增区间为 e ,单调减区间为 e ;
(2) .
【分析】
(1)当 时, , ,
所以 ,易知 e 时 , e 时 .
函数 的单调增区间为 e ,减区间为 e ;
(2)通过题意得 , .
当 e 时 , e 时 .
的单调增区间为 e ,减区间为 e ,则 e e e ,
∵ 恒成立,
∴ e e ,则 e e .故 e e ,
令 e ,e e ,
设 ( ),则 .
当 时 ,当 时 .
∴ 在 上递减,在 上递增,
综上所述 的最小值为 ln .
22、
【答案 】
(1) ;(2)3.
【分析】
解:(1)将 , 代入 ,
得曲线C 的直角坐标方程为 ,
∴曲线C的参数方程为 (α为参数).
∵曲线C过原点O,∴ ,得 ;
2 ( )当 时,曲线C的极坐标方程为 ,
将 代入 ,得 .
设A、B两点对应的极径分别为 , ,
∴ , ,
∴ .
23、
【答案 】
(1)
(2)
【分析】
(1)当 时,不等式 ,即 .
当 时, ,可得 ;
当 时, ,可得 ;
当 时, ,无解.
综上所述当 时,不等式 的解集为 .
(2)因为 ,当且仅当
时等号成立.若关于x的不等式 有解,则 ,即 ,所以实
数a的取值范围是 .
试卷(1月)
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则 ( )
A.
B.
C.
D.
2、已知复数 满足 ,则在复平面内与复数 对应的点的坐标为( )
A.
B.
C.
D.
3、下列函数在区间 上是增函数的是
A.
B. log
C.
D.
4、已知椭圆 的左右焦点分别为 , ,若椭圆上存在点 ,使
,则该椭圆离心率的取值范围为( )
A.
B.
C.
D.
5、下列函数中同时具有以下性质的是( )
①最小正周期是 ; ②图象关于直线 对称;
③在 上是增函数; ④图象的一个对称中心为 .
A.
B.
C.
D.
6、现有甲、乙两台机床同时生产直径为40mm的零件,从两台机床生产的零件中各抽取10件进行测量,其结果
如图所示,则下列选项中不能从图中数据直接比较大小的是
A.极差
B.方差
C.平均数
D.众数
7、某食堂一窗口供应2荤3素共5种菜,甲、乙两人每人在该窗口打2种菜,且每人至多打1种荤菜,则两人打菜
方法的种数为( )
A.64
B.81
C.36
D.100
8、如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,
现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①②
B.①③
C.①④
D.①⑤
9、命题 若 ,则 ;命题 ,使得 ,则下列命题中为真命题的是( )
A.
B.
C.
D.
10、体积为1的正方体的内切球的体积是( )
A.
B.
C.
D.
11、已知函数 ,若 .且 ,则 的取值范围是( )
A.
B.
C.
D.
12、已知函数 .若 恰有4个零点,则实数 的取值范围是
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知双曲线 的渐近线方程为 ,则 .
14、已知向量 ,则 在 上的投影向量的坐标为 .
15、如图,在直三棱柱ABC-A1B1C1中, , , , ,F为棱AA1上的一动点,则
当BF+FC1最小时,△BFC1的面积为 .
16、已知 ,且 , ,则 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知 为等差数列 的前 项和,且 .记 ,其中 表示不超过 的最大整数,如
= , .
(1)求
(2)求数列 的 前200项和.
18、(本小题8分)
由于一线城市普遍存在着交通道路拥挤的情况,越来越多的上班族选择电动车作为日常出行的重要工具,而续
航里程数则是作为上班族选择电动车的重要标准之一.现将某品牌旗下的一新款电动车的续航里程数作了抽检
(共计1000台),所得结果统计如下图所示.
(1)试估计该款电动车续航里程不低于34公里的概率;
(2)在该款电动车推出一段时间后,为了调查“购买者的 性别”与“使用的满意程度”是否相关,客服人员随机抽
取了200名用户进行反馈调查,所得情况如下表所示:
满意 不满意
男性用户 60 40
女性用户 50
则根据上述数据,能否在犯错误的概率不超过0.05的前提下认为“购买者的性别”与“使用的满意程度”有关?
(3)为了提高用户对电动车续航里程的满意度,工作人员将检测的续航里程在 \left[ 30,32 ight) 之间的电动车 的
电瓶进行更换,并使得该部分电动车的续航里程均匀分布于另外五组,分别求出电瓶更换前与更换后被检测的
电动车的平均续航里程,并计算更换后比更换前的平均续航里程多了多少.
附参考公式: {{K}^{2}}=\frac{n{{\left( ad-bc ight)}^{2}}}{\left( a+b ight)\left( c+d ight)\left( a+c ight)\left( b+d ight)} .
P\left( {{K}^{2}}\ge k ight) 0.100 0.050 0.010 0.001
2.706 3.841 6.635 10.828
19、(本小题8分)
如图,在棱长为2的正方体 中,E为 的中点.
(1)求证: 平面 ;
(2)求平面 与平面 夹角的余弦值.
20、(本小题10分)
已知抛物线 截直线 所得弦长 .
(1)求m的值;
(2)设P是x轴上 的点,且 的面积为9,求点P的坐标.
21、(本小题12分)
已知函数
(1)当 时,求函数 的单调区间;
(2)若 恒成立,求 的最小值.
22、(本小题12分)
以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ﹣ ,直
线l的极坐标方程为 ( ).
(1)求曲线C的参数方程,若曲线C过原点O,求实数a的值;
(2)当 时,直线l与曲线C交于A,B两点,求 .
23、(本小题12分)
设函数 .
(1)当 时,求不等式 的解集;
(2)若关于x的不等式 有解,求实数a的取值 范围.
参考答案
一、单选题
1、
【答 案】
B
【分析】
由 ,则 ,即 ,由 ,则 ,
因此正确答案为:B.
2、
【答 案】
B
【分析】
,
复数 对应的点的坐标为 .
因此正确答案为:B.
3、
【答 案】
B
【分析】
A.函数y=4﹣5x在R上单调递减,为减函数.
B.函数y=log 3x+1在(0,+∞)上单调递增,∴在区间(0,2)上是增函数,正确.
C.函数y=x2﹣2x+3的对称轴为x=1,∴函数在(﹣∞,1)上单调递减,在(1,+∞)上单调递增,∴C有误.
D .函数y=﹣2x,在R上单调递减,为减函数.
因此正确答案为B.
4、
【答 案】
C
【分析】
由椭圆的定义知: ,
因为 ,即 ,
又因为 ,所以 ,
所以有: ,
,
故椭圆的离心率的取值范围是 .
因此正确答案为:C
5、
【答 案】
D
【分析】
对A:函数的最小正周期为 ,故A不正确;
对B:该函数在区间 为减函数,故B不正确;
对C:函数图像不关于 直线对称,故C不正确;
对D:该函数满足四条性质,故D正确.
因此正确答案为:D.
6、
【答 案】
C
【分析】
由于极差反映所有数据中最大值与最小值的差的大小,
方差反映所有数据的波动大小,
平均数反映所有数据的平均值的 大小,
众数反映所有数据中出现次数最多的数的 大小,
因此由图象可以知不能从图中数据直接比较平均 数的大小.
因此正确答案为:C
7、
【答 案】
B
【分析】
甲有两种情况:一荤一素, 种;两素, 种.故甲共有 种,同理乙也有9种,则两人打菜
方法的种数为 种.因此正确答案为B.
8、
【答 案】
D
【分析】
一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是矩形除去一条边,
当截面经过圆柱上下底面的圆心时,圆锥的截面为三角形除去一条边,所以①无误;
当截面不经过圆柱上下底面的圆心时,圆锥的截面为抛物线的一部分,所以⑤正确;
因此正确答案为:D
9、
【答 案】
C
【分析】
若 ,则 ,在 时不成立,故 是假命题;
,使得 ln ,故命题 为真命题,
故命题 , , 是假命题,命题 是真命题.
因此正确答案为:C
10、
【答案 】
A
【分析】
如下图所示,因为正方体的体积为1,所以其边长为1
其内切球的球心为正方体的中心 ,半径为
则球的体积为 .
因此正确答案为:A
11、
【答 案】
B
【分析】
的图象如下:
因为 .且
所以 且
所以 ,所以
所以
当且仅当 ,即 时等号成立
因此正确答案为:B
12、
【答 案】
A
【分析】
恰有4个零点等价于方程 有四个不同的根,
等价于y 的图象有四个不同的交点,
作出y 的图象,
由图象可以知 时,两图象有三个 交点,
由 ,由 ,
此时 过y h x ln 上的点 ,h x ,
所以h ,即 与y ln 相切,
可得 时,两图象有两个交点,
由图象可以知,当 时,y 的图象有四个不同的交点,
即 恰有4个零点,
所以,若 恰有4个 零点,则实数 的取值范围是 ,因此正确答案为A.
二、填空题
13、
【答案 】
【分析】
当 时,双曲线 的渐近线方程为 ,
通过题意得 ,解得 .
因此正确答案为 .
14、
【答案 】
【分析】
利用向量的投影向量公式,代入坐标进行计算即可.
【详解】
解:向量 , ,
在 上的投影向量的坐标为: , .
故答案为: , .
15、
【答案 】
【分析】
解:通过题意得
将直三棱柱 的侧面沿 剪开,并展开到同一平面上,如下图所示:
连接 ,则 与 的交点即为 最小时的点 .
在展开图中, , , .
又由 易知,
由此可知
在直三棱柱 中,
在 中,
故△BFC1的面积为
因此正确答案为:
16、
【答案 】
【分析】
因为 ,且 , ,所以 ,
则 ,
,
因此 .
因此正确答案为: .
三、解答题
17、
【答案 】
(1) ; ;
(2)524
【分析】
(1)设等差数列 的公差为d,
由已知 = ,根据等差数列性质可知:
∴ . ∵ ,所以
∴
∴ log , log , log .
(2 )当 时, , log ,共2项;
当 时, log ,共10项;
当 时, log ,共50项;
当 时, log ,共138 项.
∴ 数列 的前200项和为 .
18、
【答案 】
(1)0.8;(2)表格见解析,不能;(3)36.5(公里),36.8(公里),更换后比更换前的平均续航里程多了
0.3公里.
【分析】
解:(1)由频率分布直方图可知该款电动车续航里程不低于34公里的频率为
,故该款电动车续航里程不低于34公里的概率的
估计值为0.8.
(2)通过题 意,得到 列联表如下:
满意 不满意 总计
男性用户 60 40 100
女性用户 50 50 100
总计 110 90 200
则 的观测值
k=\frac{200 imes {{\left( 60 imes 50-40 imes 50 ight)}^{2}}}{100 imes 100 imes 110 imes 90}=\frac{200}{99}\approx 2.020< 3.841
,故不能在犯错误的概率不超过0.05的前提下认为“购买者的性别”与“使用的满意程度”有关;
(3)通过题意,电瓶更换前被检测电动车的平均续航里程为
(公里)
电瓶更换后被检 测电动车的平均续航里程为
(公里)
故更换后比更换 前的平均续航里程多了0.3公里.
19、
【答 案】
(1)证明见解析
(2)
【分析】
(1)证明:由正方体的性质可知, ,且 ,
所以四边形 是平行四边形,
所以 .
因为 平面 , 平面 ,
所以 平面 .
(2)以A为原点, 、 、 分别为x轴、y轴、z轴,建立如下图所示的空间直角坐标系.
则 ,
所以 , , ,
设平面 的法向量为 ,
则 ,令 ,则 , , ,
易知平面 的一个法向量为 , ,
所以 ,
所以平面 与平面 夹角的余弦值为 .
20、
【答案 】
(1) ;(2) 或 .
【分析】
(1)设 .
由 ,得 ,
,
由根与系数的关系得 .
∴
,
∵ ,∴ ,
解得 .
(2)由(1) 知直线 的方程为 .
设 ,点P到直线 的距离为d,
则 .
又 ,则 ,
∴ ,
∴ ,
∴ 或 .
故点P的坐标为 或 .
21、
【答 案】
(1) 单调增区间为 e ,单调减区间为 e ;
(2) .
【分析】
(1)当 时, , ,
所以 ,易知 e 时 , e 时 .
函数 的单调增区间为 e ,减区间为 e ;
(2)通过题意得 , .
当 e 时 , e 时 .
的单调增区间为 e ,减区间为 e ,则 e e e ,
∵ 恒成立,
∴ e e ,则 e e .故 e e ,
令 e ,e e ,
设 ( ),则 .
当 时 ,当 时 .
∴ 在 上递减,在 上递增,
综上所述 的最小值为 ln .
22、
【答案 】
(1) ;(2)3.
【分析】
解:(1)将 , 代入 ,
得曲线C 的直角坐标方程为 ,
∴曲线C的参数方程为 (α为参数).
∵曲线C过原点O,∴ ,得 ;
2 ( )当 时,曲线C的极坐标方程为 ,
将 代入 ,得 .
设A、B两点对应的极径分别为 , ,
∴ , ,
∴ .
23、
【答案 】
(1)
(2)
【分析】
(1)当 时,不等式 ,即 .
当 时, ,可得 ;
当 时, ,可得 ;
当 时, ,无解.
综上所述当 时,不等式 的解集为 .
(2)因为 ,当且仅当
时等号成立.若关于x的不等式 有解,则 ,即 ,所以实
数a的取值范围是 .
同课章节目录
