2022~2023学年陕西西安长安区长安区第一中学高二下学期期末文科数学试卷(图片版,含解析)
文档属性
| 名称 | 2022~2023学年陕西西安长安区长安区第一中学高二下学期期末文科数学试卷(图片版,含解析) |  | |
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 10:56:27 | ||
图片预览




文档简介
2022~2023学年陕西西安长安区长安区第一中学高二下学期期末文科数学
试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则 ( )
A.
B.
C.
D.
2、已知复数 ( ,i为虚数单位),满足 ,则 ( )
A.
B.3
C.
D.5
3、下列命题正确的是( )
A.“ ”是“ ”的必要不充分条件
B.对于命题 : ,使得 ,则 : 均有
C.若 为真命题,则 , 至少有一个为真命题
D.命题“若 ,则 ”的否命题为“若 ,则 ”
4、干支纪年法是中国历法上自古以来就一直使用的纪年方法、干支是天干和地支的总称,甲、乙、丙、丁、
戊、己、庚、辛、壬、癸为天干:子、丑、寅、卯、辰、已、午、未,申、酉、戌、亥为地支.把十天干和十二
地支依次相配,如甲对子、乙对丑、丙对寅、…癸对寅,其中天干比地支少两位,所以天干先循环,甲对戊、
乙对亥、…接下来地支循环,丙对子、丁对丑、.,以此用来纪年,今年2020年是庚子年,那么中华人民共和国
建国100周年即2049年是( )
A.戊辰年
B.己巳年
C.庚午年
D.庚子年
5、执行如图所示的程序框图.如果输入的 为2,输出的 为4,那么 ( )
A.13
B.14
C.15
D.16
6、已知 中, ,点 在平面 内, ,则 的最大值为
( )
A.6
B.4
C.
D.
7、若 ,且 ,则 ( )
A.
B.-1
C.1
D.2
8、在 中, ,则 的取值范围为( )
A.
B.
C.
D.
9、已知四面体ABCD的所有顶点在球O的表面上, 平面BCD , , ,
,则球O的表面积为( )
A.
B.
C.
D.
10、袋中装有标号分别为1,2,3,4的四个大小相同的小球,现从中有放回地取两次(每次只取一个球),则
两次取出的小球的标号数之差的绝对值不大于2的概率是( )
A.
B.
C.
D.
11、如图所示, , 是双曲线 : ( , )的左、右焦点, 的右支上存在一点 满足
, 与双曲线 左支的交点 满足 ,则双曲线 的渐近线方程为( )
A.
B.
C.
D.
12、已知函数 有两个零点 、 ,且存在唯一的整数 ,则实数 的取值范围是
( )
A.
B.
C.
e
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、某校为了解学生学习的情况,采用分层抽样的方法从高一 人、高二 人、高三 人中,抽取 人进
行问卷调查. 已知高一被抽取的人数为 ,那么高三被抽取的人数为 .
14、已知实数 满足条件: ,则 的最大值为 .
15、将函数 的图象向右平移 个单位长度后得到函数 的图象,若 在区间
上单调递增,则满足条件的实数 的取值范围是 .
16、已知函数 及其导函数 定义域均为R,记函数 ,若函数 的图象关于点 中心
对称, 为偶函数,且 则 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知数列 满足, , .
(1)若数列 为数列 的奇数项组成的数列,证明:数列 为等差数列;
(2)求数列 的前50项和.
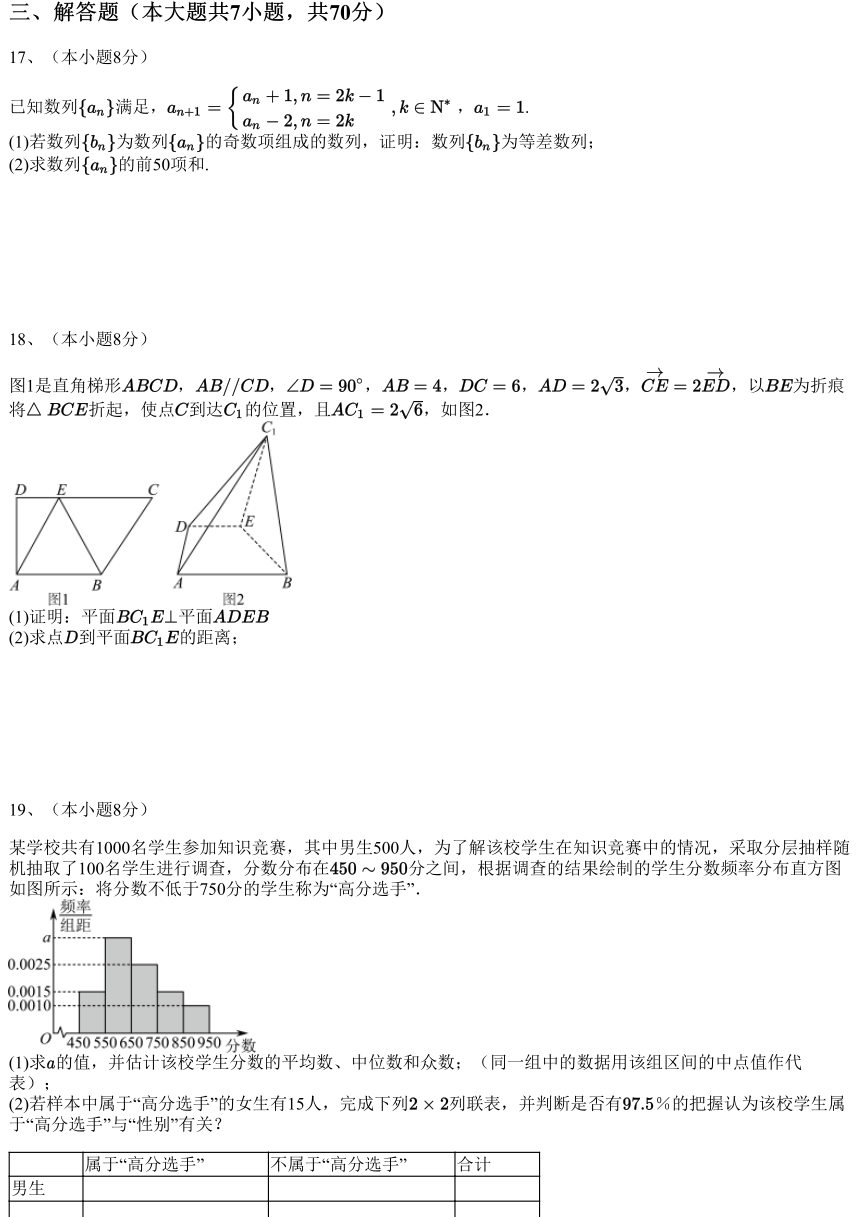
18、(本小题8分)
图1是直角梯形 , , , , , , ,以 为折痕
将 折起,使点 到达 的位置,且 ,如图2.
(1)证明:平面 平面
(2)求点 到平面 的距离;
19、(本小题8分)
某学校共有1000名学生参加知识竞赛,其中男生500人,为了解该校学生在知识竞赛中的情况,采取分层抽样随
机抽取了100名学生进行调查,分数分布在 分之间,根据调查的结果绘制的学生分数频率分布直方图
如图所示:将分数不低于750分的学生称为“高分选手”.
(1)求 的值,并估计该校学生分数的平均数、中位数和众数;(同一组中的数据用该组区间的中点值作代
表);
(2)若样 本中属于“高分选手”的女生有15人,完成下列 列联表,并判断是否有 %的把握认为该校学生属
于“高分选手”与“性别”有关?
属于“高分选手” 不属于“高分选手” 合计
男生
女生
合计
(参考公式: ,期中 )
20、(本小题10分)
已知函数 (e 是自然对数的底数), 是 的导数, .
(1)求 的单调区间;
(2)证明:对任意的 , .
21、(本小题12分)
已知椭圆 : ( )的左、右焦点分别为 , 为椭圆上的一点, 的周长为
6, 的最小值为1, 为抛物线 的焦点.
(1)求椭圆 与抛物线 的方程;
(2)过椭圆 的左顶点 的直线 交抛 物线 于 两点,点 为原点,射线 分别交椭圆于 两点,
的面积为 , 的面积为 ,则是否存在直线 使得 ?若存在,求出直线 的方程;若
不存在,请说明理由.
22、(本小题12分)
在平面直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点, 轴正半
轴为极轴建立极坐标系,已知直线 的极坐标方程为 .
(1)写出直线 的参数方程及曲线 的普通方程;
(2)设点 ,若直线 与曲线 交于A,B两点,且 ,求实数 的值.
23、(本小题12分)
设函数 , .
(1) 当 时,求不等式 的解集;
(2)对任意 ,恒有 ,求实 数 的取值范围.
参考答案
一、单选题
1、
【答 案】
B
【分析】
由对数函数的定义域可知集合 ,再求的 ,再由交集的定义即可求得
.
【详解】
得 即 ,
因为 ,所以 ,
则 .
故选:B.
2、
【答 案】
A
【分析】
由 求得共轭复数,再代入 中求得 ,再计算 即可.
【详解】
因为 所以 ,则 ,解得 ,
.
故选:A.
3、
【答 案】
C
【分析】
A选项,由必要,充分条件定义可得答案;B选项,由特称命题的否定相关知识可判断选项正误;C选项,由逻
辑连接词或的含义可判断选项正误;D选项,由原命题与否命题关系可判断选项正误.
【详解】
A选项, 或 ,则“ ”是“ ”的充分不必要条件,故A错误;
选项B,命题 : ,使得 ,则 : ,均有 ,故B错误;
C选项,因 为真命题,则 或 为真命题,故C正确;
D选项,命题“若 ,则 ”的否命题为“ 若 ,则 ”,故D错误.
故选:C
4、
【答 案】
B
【分析】
由题意2020年是干支纪年法中的庚子年,则2049的天干为己,地支为 巳,即可求出答案.
【详解】
天干是以 10为一周期,地支是以12为一周期,
2020年是干支纪年法中的庚子年,而 ,所以2049的天干为己,地支
为 已,
故选:B .
【点睛】
本题考查 数学文化,实际生活中的数学应用,关键在于运用阅读理解能力将生活中的数据和用语转化为数学中
的概念和数据,属于中档题.
5、
【答 案】
C
【分析】
由程序框图可知,输出的 ,
则 ,得 ,那么判断框图 .
因此正确答案为:C.
6、
【答 案】
A
【分析】
根据已知条件及勾股定理的逆定理,利用锐角三角函数、向量的线性运算和向量的数量积运算,结合两角差的
余弦公式及正弦函数的性质即可求解.
【详解】
由 ,得 ,所以 ,
在 中, , ,
又点 在平面 内, ,如图所示
设 , ,则 ,
所以
.
因为 ,
所以 ,即 ,
所以 的最大值为 .
故选:A.
7、
【答 案】
D
【分析】
利用诱导公式可得 ,即 ,再根据商数关系化弦为切,求出
,再根据两角差的正切公式即可得解.
【详解】
因为 ,所以 ,
由 ,得 ,
即 ,
所以 ,即 ,解得 或 (舍),
所以 .
故选:D.
8、
【答 案】
A
【分析】
利用正弦定理边角化及三角形的内角和定理,结合两角的正弦公式及两角和的余弦公式,再利用余弦函数的性
质即可求解.
【详解】
由 及正弦定理,得 ,
,
又 ,
5π
,
.
又 ,
,
,
,
的取值范围为 .
故选:A.
9、
【答 案】
D
【分析】
先求出 的外接圆半径,作出辅助线,得到球心的位置,利用外接球半径相等得到方程,求出半径和表
面积.
【详解 】
因为 , ,设 的外接圆半径为 ,
则由正弦定理得 ,则 ,
如图所示,点 为 的外接圆圆心,连接 ,则 ,
设外接球球心为 ,则 ⊥平面 ,设 ,
过点 作 ⊥ 于点 ,连接 ,
则 , ,
由勾股定理得 , ,
故 ,解得 ,
所以外接球的半径为 ,
所以球O的表面积为 .
故选:D
【点睛】
关键点点睛 :解决与球有关的内切或外接的问题时,解题的关键是确定球心的位置.对于外切的问题要注意球
心到各个面的距离相等且都为球半径;对于球的内接几何体的问题,注意球心到各个顶点的距离相等,解题时
要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形,利用勾股定理求得球的半径
10、
【答案 】
D
【分析】
根据独立事件的乘法公式和互斥事件的加法公式可求出结果.
【详解】
当两次取出的小球的标号数之差的绝对值为 时, ,
当两次取出的小球的标号数之差的绝对值为 时, ,
当两次取出的小球的标号数之差的绝对值为 时, ,
所以所求概率 .
故选:D
11、
【答 案】
B
【分析】
在 和 中,由正弦定理结合已知条件可得 ,设 ,由双曲
线的定义和勾股定理可得 ,再由 即可求得结果.
【详解】
在 中,由正弦定理得, ①,
在 中,由正弦定理得, ②,
因为 ,所以 ,
所以①式与②式相比,得
,
因为 ,
所以 ,
所以 ,
设 ,则
由双曲线的定义得 , ,
因为 ,所以 ,
所以 ,解得 ,
在 中,由勾股定理得 ,
所以 ,得 ,
所以 ,得 ,
所以双曲线 的渐近线方程为 ,
故选:B
【点睛】
关键点点 睛:此题考查双曲线的离心率,考查的关键是在 和 中利用正弦定理结合已知条件可
得 ,再利用勾股定理和双曲线的定义可求得 的关系,考查数学计算能力,属于较难题.
12、
【答案 】
B
【分析】
由题意可知 ,构造函数 ,利用导数研究函数 的单调性及极值,又
时, ;当 时, ,作出函数 的图像,利用数形结合思想即可求解.
【详解】
由题意 ,得 ,
设 ,求导
令 ,解得
当 时, , 单调递增;当 时, , 单调递减;
故当 时,函数取得极大值,且
又 时, ;当 时, ,故 ;
作出函数大致图像,如图所示:
又 ,
因为存在唯一的整数 ,使得 与 的图象有两个交点,
由图可知: ,即
故选:B.
【点睛】
方法点睛 :已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范 围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面 直角坐标系中画出函数的图象,利用
数形结合的方法求解.
二、填空题
13、
【答案 】
24
【分析】
根据分层抽样抽样比可求出结果.
【详解】
依题意得 ,得 ,
所以高三被抽取的人数为 .
故答案为: .
14、
【答案 】
1
【分析】
画出不等式组表示的可行域,由 可知表示过可行域中点 和点 的直线的斜率,
然后图形求出斜率的最大值即可.
【详解】
不等式组 表示的可行域如图所示,
由 可知表示过可行域中点 和点 的直线的斜率,
由图可知当直线过点 时,直线的斜率最大,即 取得最大值,
由 ,得 ,则 ,
所以 的最大值为 ,
故答案为:1
15、
【答案 】
π π
【分析】
先求出 ,再由正弦型函数的单调性即可求解.
【详解】
,
将函数 的图象向右平移 个单位长度得到函数 的图象,
π
因为 ,所以 ,
因为函数 在区间 上是单调递增,
π π π π
所以 ,解得: ,
π π π π π
又因为 ,
π π
所以实数 的取值范围是 .
π π
故答案为:
16、
【答 案】
678
【分析】
由 的图象关于点 中心对称结合导数可知 ,再结合 为偶函数可知
的一个周期为3, .又注意到 即可得答案.
【详解】
因 的 图象关于点 中心对称,则
.
因 为偶函数,根据函数的伸缩变化可知 也是偶函数,
所以 .
则 ,即 的一个周期为3.令 ,由 可得 .
注意到 ,则
.
故答案为:678
三、解答题
17、
【答案 】
(1)证明见解析
(2)
【分析】
(1)由题设递推式可得 ,据此可得答案;
(2)设 为数列 的偶数项组成的数列,由题可得 数列 是首项为2,公差为 的等差数列,后由分组
求和法可得答案.
【详解】
(1)由题 , ,
且 ,所以数列 是首项为1,公差为 的等差数列;
(2)设 为数列 的偶数项组成的数列,注意到 ,
,
所以数列 是首项为2,公差为 的等差数列,
结合 可知, 的奇数项和偶数项都是以 为公差的等差数列,
所以
.
18、
【答 案】
(1)证明见解析
(2)
【分析】
(1)利用已知条件得四边形 为菱形,连接 交 于点 ,得 ,再利用长度关系得到
,再由线面垂直的判定可得 平面 ,从而得到平面 平面 ;
(2)计算出 ,并计算出 的面积,利用等体积法可求得点 到平面 的距离 .
【详解】
(1)如图 所示:
连接AC,交BE于F,
因为 , , , , ,所以AE=4,
又 ,所以四边形ABCE是菱形,所以 ,
在 中, ,所以 ,
在 中,又 , ,则 ,
所以 ,又 , 面 ,所以 平面 ,
又因为 面 ,所以平面 平面
(2)设点D到平面 的距离为h,
因为 ,
且 ,所以 ,
即 ,解得 .
19、
【答 案】
(1) ,平均数670,中位数650,众数600
(2)列联表见解析;没有
【分析】
(1)由频率和为1可得a值,由直方图中众数、平均数和中位数的计算公式进行计算即可;
(2)由题意得到2×2列联表,然后计算 的观测值 ,然后与题目中表格的数据进行比较 即可得到结论.
【详解】
(1)由题 意知 ,
解得 ,
样本平均数 ,
易得中位数为650,众数为600.
(2)由题可知,样本中男生50人 ,女生50人,属于“高分选手”的 人,其中女生10人;
得出以下 列联表;
属于“高分选手” 不属于“高分选手” 合计
男生 10 40 50
女生 15 35 50
合计 25 75 100
,
所以没有 %的把握认为该校学生属于“高分选手”与性别有关.
20、
【答 案】
(1) 增函数区间为 ,单调减区间为
(2)证明见解析
【分析】
(1)由题可得 ,结合 在 上的正负性可得 的单调区间;(2)构造函数
利用其单调性证明 ,再证明 即可.
【详解】
(1)由题 ,令 ,则 ,即 在 上单
调递减,又注意到 .
则当 时, ;当 时, .
于是 增函数区间为 ;单调减区间为 ;
(2) .
因此对任意的 , .
设 ,则 .
令 在 上单调递增; 在
上单调递减;
则 ,故 .
设 ,则 , 在 上单调递增,则
.
e
∴ ,即对任意的 , e = .
e
【点睛】
关键点睛:本题涉及求函数单调区间及利用导数证明不等式.函数单调区间与其导函数正负性关系密切.本题不等
式证明直接证明较为复杂,注意到 ,故再证明 即可.
21、
【答 案】
(1) ,
(2) 或
【分析】
(1)根据题意,由焦点三角形的周长公式,以及两点之间距离公式结合二次函数性质,列出方程组,根据椭圆
与抛物线的标准方程,可得答案;
(2)根据题意设出直线 的方程,联 立直线与抛物线,写出韦达定理,根据题目中的面积关系,列出等式,结
合设出的点,写出射线所在直线的方程,联立其与椭圆,整理等式,可得答案.
【详解】
(1)由题 意可作图如下:
的周长为 ,
设 ,则 ,由 ,则 ,
由 ,即 ,
令 ,其对称轴为 ,
则函数 在 上单调递减,即 ,
所以 ,
由题意得 ,解得 ,椭圆的方程为 ,
,所以抛物线的方程为 .
(2)由题意可作图如下:
由题意得直线l的斜率不为0, ,
设直线l的方程为 ,设 ,
由 ,得 ,∴ , ,
∵ , ,
∵ ,∴ 直线OA的斜率为 ,即直线OA的方程为 ,
由 ,得 ,同理可得 ,
,
,得 ,
∴ 存在直线l,方程为 或 .
22、
【答案 】
(1)直线 的参数方程为 ( 为参数),曲线 的普通方程为
(2)
【分析】
(1)将直线 的极坐标方程化为普通方程,再将直线 的普通方程化为参数方程即可,直接消去参数将曲线 的
参数方程化为普通方程即可;
(2)设 、 对应的参数分别 为 、 ,将直线 的参数方程与曲线 的普通方程联立,结合 ,得到关
于 的等式,再求出 的值即可.
【详解】
(1)因为 ,所以 ,
又因为 , ,即 ,
所以直线 的普通方程可化简为 ,
所以直线 的参数方程为 ( 为参数),
由 ,消去 得 ,
所以曲线 的普通方程 .
(2)由 ,知 与 反向,所以点 在圆内,
所以 ,解得 ,
联立直线 的参数方程和曲线 的普通 方程,可得 ,
设 、 对应的参数分别为 、 ,
因为点 在圆内,则直线 必与 圆相交,
由韦达定理,可得 ①, ②,
由于 ,代入①可得 ,代入②可得 ,
所以 ,解得 ,合乎题意.
综上所述, .
23、
【答案 】
(1)
(2)
【分析】
(1)由绝对值不等式的解法,当a=2,分 , , 三种情况讨论,求解不等式即可得解;
(2)分析可得原题意等价于 \min~ ,结合绝对值不等式分析运算.
【详解】
(1)当 时,可得 ,
当 时,则 ,解得 ,此时得 ;
当 时,则 ,此时无解;
当 时,则 ,解得 ,此时得 ;
综上所述:不等式 的解集为 .
(2)对任意 ,恒有 ,等价于 \min~ ,
因为 ,当且仅当 时,等号成立
所以 ,且 ,
即 ,解得 或 ,
所以实数 的取值范围为 .
【点睛】
考查绝对值 不等式的解法,不等式恒成立问题,考查逻辑推理、数学运算的核心素养.
试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则 ( )
A.
B.
C.
D.
2、已知复数 ( ,i为虚数单位),满足 ,则 ( )
A.
B.3
C.
D.5
3、下列命题正确的是( )
A.“ ”是“ ”的必要不充分条件
B.对于命题 : ,使得 ,则 : 均有
C.若 为真命题,则 , 至少有一个为真命题
D.命题“若 ,则 ”的否命题为“若 ,则 ”
4、干支纪年法是中国历法上自古以来就一直使用的纪年方法、干支是天干和地支的总称,甲、乙、丙、丁、
戊、己、庚、辛、壬、癸为天干:子、丑、寅、卯、辰、已、午、未,申、酉、戌、亥为地支.把十天干和十二
地支依次相配,如甲对子、乙对丑、丙对寅、…癸对寅,其中天干比地支少两位,所以天干先循环,甲对戊、
乙对亥、…接下来地支循环,丙对子、丁对丑、.,以此用来纪年,今年2020年是庚子年,那么中华人民共和国
建国100周年即2049年是( )
A.戊辰年
B.己巳年
C.庚午年
D.庚子年
5、执行如图所示的程序框图.如果输入的 为2,输出的 为4,那么 ( )
A.13
B.14
C.15
D.16
6、已知 中, ,点 在平面 内, ,则 的最大值为
( )
A.6
B.4
C.
D.
7、若 ,且 ,则 ( )
A.
B.-1
C.1
D.2
8、在 中, ,则 的取值范围为( )
A.
B.
C.
D.
9、已知四面体ABCD的所有顶点在球O的表面上, 平面BCD , , ,
,则球O的表面积为( )
A.
B.
C.
D.
10、袋中装有标号分别为1,2,3,4的四个大小相同的小球,现从中有放回地取两次(每次只取一个球),则
两次取出的小球的标号数之差的绝对值不大于2的概率是( )
A.
B.
C.
D.
11、如图所示, , 是双曲线 : ( , )的左、右焦点, 的右支上存在一点 满足
, 与双曲线 左支的交点 满足 ,则双曲线 的渐近线方程为( )
A.
B.
C.
D.
12、已知函数 有两个零点 、 ,且存在唯一的整数 ,则实数 的取值范围是
( )
A.
B.
C.
e
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、某校为了解学生学习的情况,采用分层抽样的方法从高一 人、高二 人、高三 人中,抽取 人进
行问卷调查. 已知高一被抽取的人数为 ,那么高三被抽取的人数为 .
14、已知实数 满足条件: ,则 的最大值为 .
15、将函数 的图象向右平移 个单位长度后得到函数 的图象,若 在区间
上单调递增,则满足条件的实数 的取值范围是 .
16、已知函数 及其导函数 定义域均为R,记函数 ,若函数 的图象关于点 中心
对称, 为偶函数,且 则 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知数列 满足, , .
(1)若数列 为数列 的奇数项组成的数列,证明:数列 为等差数列;
(2)求数列 的前50项和.
18、(本小题8分)
图1是直角梯形 , , , , , , ,以 为折痕
将 折起,使点 到达 的位置,且 ,如图2.
(1)证明:平面 平面
(2)求点 到平面 的距离;
19、(本小题8分)
某学校共有1000名学生参加知识竞赛,其中男生500人,为了解该校学生在知识竞赛中的情况,采取分层抽样随
机抽取了100名学生进行调查,分数分布在 分之间,根据调查的结果绘制的学生分数频率分布直方图
如图所示:将分数不低于750分的学生称为“高分选手”.
(1)求 的值,并估计该校学生分数的平均数、中位数和众数;(同一组中的数据用该组区间的中点值作代
表);
(2)若样 本中属于“高分选手”的女生有15人,完成下列 列联表,并判断是否有 %的把握认为该校学生属
于“高分选手”与“性别”有关?
属于“高分选手” 不属于“高分选手” 合计
男生
女生
合计
(参考公式: ,期中 )
20、(本小题10分)
已知函数 (e 是自然对数的底数), 是 的导数, .
(1)求 的单调区间;
(2)证明:对任意的 , .
21、(本小题12分)
已知椭圆 : ( )的左、右焦点分别为 , 为椭圆上的一点, 的周长为
6, 的最小值为1, 为抛物线 的焦点.
(1)求椭圆 与抛物线 的方程;
(2)过椭圆 的左顶点 的直线 交抛 物线 于 两点,点 为原点,射线 分别交椭圆于 两点,
的面积为 , 的面积为 ,则是否存在直线 使得 ?若存在,求出直线 的方程;若
不存在,请说明理由.
22、(本小题12分)
在平面直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点, 轴正半
轴为极轴建立极坐标系,已知直线 的极坐标方程为 .
(1)写出直线 的参数方程及曲线 的普通方程;
(2)设点 ,若直线 与曲线 交于A,B两点,且 ,求实数 的值.
23、(本小题12分)
设函数 , .
(1) 当 时,求不等式 的解集;
(2)对任意 ,恒有 ,求实 数 的取值范围.
参考答案
一、单选题
1、
【答 案】
B
【分析】
由对数函数的定义域可知集合 ,再求的 ,再由交集的定义即可求得
.
【详解】
得 即 ,
因为 ,所以 ,
则 .
故选:B.
2、
【答 案】
A
【分析】
由 求得共轭复数,再代入 中求得 ,再计算 即可.
【详解】
因为 所以 ,则 ,解得 ,
.
故选:A.
3、
【答 案】
C
【分析】
A选项,由必要,充分条件定义可得答案;B选项,由特称命题的否定相关知识可判断选项正误;C选项,由逻
辑连接词或的含义可判断选项正误;D选项,由原命题与否命题关系可判断选项正误.
【详解】
A选项, 或 ,则“ ”是“ ”的充分不必要条件,故A错误;
选项B,命题 : ,使得 ,则 : ,均有 ,故B错误;
C选项,因 为真命题,则 或 为真命题,故C正确;
D选项,命题“若 ,则 ”的否命题为“ 若 ,则 ”,故D错误.
故选:C
4、
【答 案】
B
【分析】
由题意2020年是干支纪年法中的庚子年,则2049的天干为己,地支为 巳,即可求出答案.
【详解】
天干是以 10为一周期,地支是以12为一周期,
2020年是干支纪年法中的庚子年,而 ,所以2049的天干为己,地支
为 已,
故选:B .
【点睛】
本题考查 数学文化,实际生活中的数学应用,关键在于运用阅读理解能力将生活中的数据和用语转化为数学中
的概念和数据,属于中档题.
5、
【答 案】
C
【分析】
由程序框图可知,输出的 ,
则 ,得 ,那么判断框图 .
因此正确答案为:C.
6、
【答 案】
A
【分析】
根据已知条件及勾股定理的逆定理,利用锐角三角函数、向量的线性运算和向量的数量积运算,结合两角差的
余弦公式及正弦函数的性质即可求解.
【详解】
由 ,得 ,所以 ,
在 中, , ,
又点 在平面 内, ,如图所示
设 , ,则 ,
所以
.
因为 ,
所以 ,即 ,
所以 的最大值为 .
故选:A.
7、
【答 案】
D
【分析】
利用诱导公式可得 ,即 ,再根据商数关系化弦为切,求出
,再根据两角差的正切公式即可得解.
【详解】
因为 ,所以 ,
由 ,得 ,
即 ,
所以 ,即 ,解得 或 (舍),
所以 .
故选:D.
8、
【答 案】
A
【分析】
利用正弦定理边角化及三角形的内角和定理,结合两角的正弦公式及两角和的余弦公式,再利用余弦函数的性
质即可求解.
【详解】
由 及正弦定理,得 ,
,
又 ,
5π
,
.
又 ,
,
,
,
的取值范围为 .
故选:A.
9、
【答 案】
D
【分析】
先求出 的外接圆半径,作出辅助线,得到球心的位置,利用外接球半径相等得到方程,求出半径和表
面积.
【详解 】
因为 , ,设 的外接圆半径为 ,
则由正弦定理得 ,则 ,
如图所示,点 为 的外接圆圆心,连接 ,则 ,
设外接球球心为 ,则 ⊥平面 ,设 ,
过点 作 ⊥ 于点 ,连接 ,
则 , ,
由勾股定理得 , ,
故 ,解得 ,
所以外接球的半径为 ,
所以球O的表面积为 .
故选:D
【点睛】
关键点点睛 :解决与球有关的内切或外接的问题时,解题的关键是确定球心的位置.对于外切的问题要注意球
心到各个面的距离相等且都为球半径;对于球的内接几何体的问题,注意球心到各个顶点的距离相等,解题时
要构造出由球心到截面圆的垂线段、小圆的半径和球半径组成的直角三角形,利用勾股定理求得球的半径
10、
【答案 】
D
【分析】
根据独立事件的乘法公式和互斥事件的加法公式可求出结果.
【详解】
当两次取出的小球的标号数之差的绝对值为 时, ,
当两次取出的小球的标号数之差的绝对值为 时, ,
当两次取出的小球的标号数之差的绝对值为 时, ,
所以所求概率 .
故选:D
11、
【答 案】
B
【分析】
在 和 中,由正弦定理结合已知条件可得 ,设 ,由双曲
线的定义和勾股定理可得 ,再由 即可求得结果.
【详解】
在 中,由正弦定理得, ①,
在 中,由正弦定理得, ②,
因为 ,所以 ,
所以①式与②式相比,得
,
因为 ,
所以 ,
所以 ,
设 ,则
由双曲线的定义得 , ,
因为 ,所以 ,
所以 ,解得 ,
在 中,由勾股定理得 ,
所以 ,得 ,
所以 ,得 ,
所以双曲线 的渐近线方程为 ,
故选:B
【点睛】
关键点点 睛:此题考查双曲线的离心率,考查的关键是在 和 中利用正弦定理结合已知条件可
得 ,再利用勾股定理和双曲线的定义可求得 的关系,考查数学计算能力,属于较难题.
12、
【答案 】
B
【分析】
由题意可知 ,构造函数 ,利用导数研究函数 的单调性及极值,又
时, ;当 时, ,作出函数 的图像,利用数形结合思想即可求解.
【详解】
由题意 ,得 ,
设 ,求导
令 ,解得
当 时, , 单调递增;当 时, , 单调递减;
故当 时,函数取得极大值,且
又 时, ;当 时, ,故 ;
作出函数大致图像,如图所示:
又 ,
因为存在唯一的整数 ,使得 与 的图象有两个交点,
由图可知: ,即
故选:B.
【点睛】
方法点睛 :已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范 围;
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面 直角坐标系中画出函数的图象,利用
数形结合的方法求解.
二、填空题
13、
【答案 】
24
【分析】
根据分层抽样抽样比可求出结果.
【详解】
依题意得 ,得 ,
所以高三被抽取的人数为 .
故答案为: .
14、
【答案 】
1
【分析】
画出不等式组表示的可行域,由 可知表示过可行域中点 和点 的直线的斜率,
然后图形求出斜率的最大值即可.
【详解】
不等式组 表示的可行域如图所示,
由 可知表示过可行域中点 和点 的直线的斜率,
由图可知当直线过点 时,直线的斜率最大,即 取得最大值,
由 ,得 ,则 ,
所以 的最大值为 ,
故答案为:1
15、
【答案 】
π π
【分析】
先求出 ,再由正弦型函数的单调性即可求解.
【详解】
,
将函数 的图象向右平移 个单位长度得到函数 的图象,
π
因为 ,所以 ,
因为函数 在区间 上是单调递增,
π π π π
所以 ,解得: ,
π π π π π
又因为 ,
π π
所以实数 的取值范围是 .
π π
故答案为:
16、
【答 案】
678
【分析】
由 的图象关于点 中心对称结合导数可知 ,再结合 为偶函数可知
的一个周期为3, .又注意到 即可得答案.
【详解】
因 的 图象关于点 中心对称,则
.
因 为偶函数,根据函数的伸缩变化可知 也是偶函数,
所以 .
则 ,即 的一个周期为3.令 ,由 可得 .
注意到 ,则
.
故答案为:678
三、解答题
17、
【答案 】
(1)证明见解析
(2)
【分析】
(1)由题设递推式可得 ,据此可得答案;
(2)设 为数列 的偶数项组成的数列,由题可得 数列 是首项为2,公差为 的等差数列,后由分组
求和法可得答案.
【详解】
(1)由题 , ,
且 ,所以数列 是首项为1,公差为 的等差数列;
(2)设 为数列 的偶数项组成的数列,注意到 ,
,
所以数列 是首项为2,公差为 的等差数列,
结合 可知, 的奇数项和偶数项都是以 为公差的等差数列,
所以
.
18、
【答 案】
(1)证明见解析
(2)
【分析】
(1)利用已知条件得四边形 为菱形,连接 交 于点 ,得 ,再利用长度关系得到
,再由线面垂直的判定可得 平面 ,从而得到平面 平面 ;
(2)计算出 ,并计算出 的面积,利用等体积法可求得点 到平面 的距离 .
【详解】
(1)如图 所示:
连接AC,交BE于F,
因为 , , , , ,所以AE=4,
又 ,所以四边形ABCE是菱形,所以 ,
在 中, ,所以 ,
在 中,又 , ,则 ,
所以 ,又 , 面 ,所以 平面 ,
又因为 面 ,所以平面 平面
(2)设点D到平面 的距离为h,
因为 ,
且 ,所以 ,
即 ,解得 .
19、
【答 案】
(1) ,平均数670,中位数650,众数600
(2)列联表见解析;没有
【分析】
(1)由频率和为1可得a值,由直方图中众数、平均数和中位数的计算公式进行计算即可;
(2)由题意得到2×2列联表,然后计算 的观测值 ,然后与题目中表格的数据进行比较 即可得到结论.
【详解】
(1)由题 意知 ,
解得 ,
样本平均数 ,
易得中位数为650,众数为600.
(2)由题可知,样本中男生50人 ,女生50人,属于“高分选手”的 人,其中女生10人;
得出以下 列联表;
属于“高分选手” 不属于“高分选手” 合计
男生 10 40 50
女生 15 35 50
合计 25 75 100
,
所以没有 %的把握认为该校学生属于“高分选手”与性别有关.
20、
【答 案】
(1) 增函数区间为 ,单调减区间为
(2)证明见解析
【分析】
(1)由题可得 ,结合 在 上的正负性可得 的单调区间;(2)构造函数
利用其单调性证明 ,再证明 即可.
【详解】
(1)由题 ,令 ,则 ,即 在 上单
调递减,又注意到 .
则当 时, ;当 时, .
于是 增函数区间为 ;单调减区间为 ;
(2) .
因此对任意的 , .
设 ,则 .
令 在 上单调递增; 在
上单调递减;
则 ,故 .
设 ,则 , 在 上单调递增,则
.
e
∴ ,即对任意的 , e = .
e
【点睛】
关键点睛:本题涉及求函数单调区间及利用导数证明不等式.函数单调区间与其导函数正负性关系密切.本题不等
式证明直接证明较为复杂,注意到 ,故再证明 即可.
21、
【答 案】
(1) ,
(2) 或
【分析】
(1)根据题意,由焦点三角形的周长公式,以及两点之间距离公式结合二次函数性质,列出方程组,根据椭圆
与抛物线的标准方程,可得答案;
(2)根据题意设出直线 的方程,联 立直线与抛物线,写出韦达定理,根据题目中的面积关系,列出等式,结
合设出的点,写出射线所在直线的方程,联立其与椭圆,整理等式,可得答案.
【详解】
(1)由题 意可作图如下:
的周长为 ,
设 ,则 ,由 ,则 ,
由 ,即 ,
令 ,其对称轴为 ,
则函数 在 上单调递减,即 ,
所以 ,
由题意得 ,解得 ,椭圆的方程为 ,
,所以抛物线的方程为 .
(2)由题意可作图如下:
由题意得直线l的斜率不为0, ,
设直线l的方程为 ,设 ,
由 ,得 ,∴ , ,
∵ , ,
∵ ,∴ 直线OA的斜率为 ,即直线OA的方程为 ,
由 ,得 ,同理可得 ,
,
,得 ,
∴ 存在直线l,方程为 或 .
22、
【答案 】
(1)直线 的参数方程为 ( 为参数),曲线 的普通方程为
(2)
【分析】
(1)将直线 的极坐标方程化为普通方程,再将直线 的普通方程化为参数方程即可,直接消去参数将曲线 的
参数方程化为普通方程即可;
(2)设 、 对应的参数分别 为 、 ,将直线 的参数方程与曲线 的普通方程联立,结合 ,得到关
于 的等式,再求出 的值即可.
【详解】
(1)因为 ,所以 ,
又因为 , ,即 ,
所以直线 的普通方程可化简为 ,
所以直线 的参数方程为 ( 为参数),
由 ,消去 得 ,
所以曲线 的普通方程 .
(2)由 ,知 与 反向,所以点 在圆内,
所以 ,解得 ,
联立直线 的参数方程和曲线 的普通 方程,可得 ,
设 、 对应的参数分别为 、 ,
因为点 在圆内,则直线 必与 圆相交,
由韦达定理,可得 ①, ②,
由于 ,代入①可得 ,代入②可得 ,
所以 ,解得 ,合乎题意.
综上所述, .
23、
【答案 】
(1)
(2)
【分析】
(1)由绝对值不等式的解法,当a=2,分 , , 三种情况讨论,求解不等式即可得解;
(2)分析可得原题意等价于 \min~ ,结合绝对值不等式分析运算.
【详解】
(1)当 时,可得 ,
当 时,则 ,解得 ,此时得 ;
当 时,则 ,此时无解;
当 时,则 ,解得 ,此时得 ;
综上所述:不等式 的解集为 .
(2)对任意 ,恒有 ,等价于 \min~ ,
因为 ,当且仅当 时,等号成立
所以 ,且 ,
即 ,解得 或 ,
所以实数 的取值范围为 .
【点睛】
考查绝对值 不等式的解法,不等式恒成立问题,考查逻辑推理、数学运算的核心素养.
同课章节目录
