第一讲 圆周运动 导学案 高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 第一讲 圆周运动 导学案 高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 407.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-03-31 20:17:24 | ||
图片预览

文档简介
第六章 圆周运动
第一讲 圆周运动
一.圆周运动中“匀速”与“非匀速”的理解
1.“匀速”与“非匀速”中“速”指的是速度的 不变,而非速度的 不变。
2.匀速圆周运动是一种非匀变速曲线运动。
二.描述圆周运动快慢的物理量
1.线速度
(1)定义:物体做圆周运动通过的弧长与所用时间的比值定义为线速度。
(2)物理意义:描述质点沿 运动的快慢。
(3)表达式:,其单位是________,其方向为圆周上该点的_________。
(4)线速度也有平均值与瞬时值之分,当△t足够小时,就是瞬时线速度,简称线速度。
(5)线速度是矢量,其方向与轨迹相切。如果物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做 。
2.角速度
(1)定义:质点所在的半径转过的角度和所用时间的比值叫做角速度。
(2)物理意义:描述质点绕 转动的快慢。
(3)表达式:,角速度的单位为______。
(4)匀速圆周运动中角速度大小、方向均不变。
(5)角速度是矢量,方向垂直于转动平面。
3.周期
(1)定义:质点运动一周所用的时间。
(2)表达式:,推导可得。
(3)匀速圆周运动的周期不变。
4.转速(频率)
(1)定义:质点做圆周运动时,单位时间内转过的圈数称为转速,符号是n,其单位为_____。
(2)周期的倒数是频率,符号是f,单位是Hz,当转速的单位取转每秒(r/s)时,频率大小等于转速大小。
(2)表达式:
5.线速度、角速度、周期、转速的关系
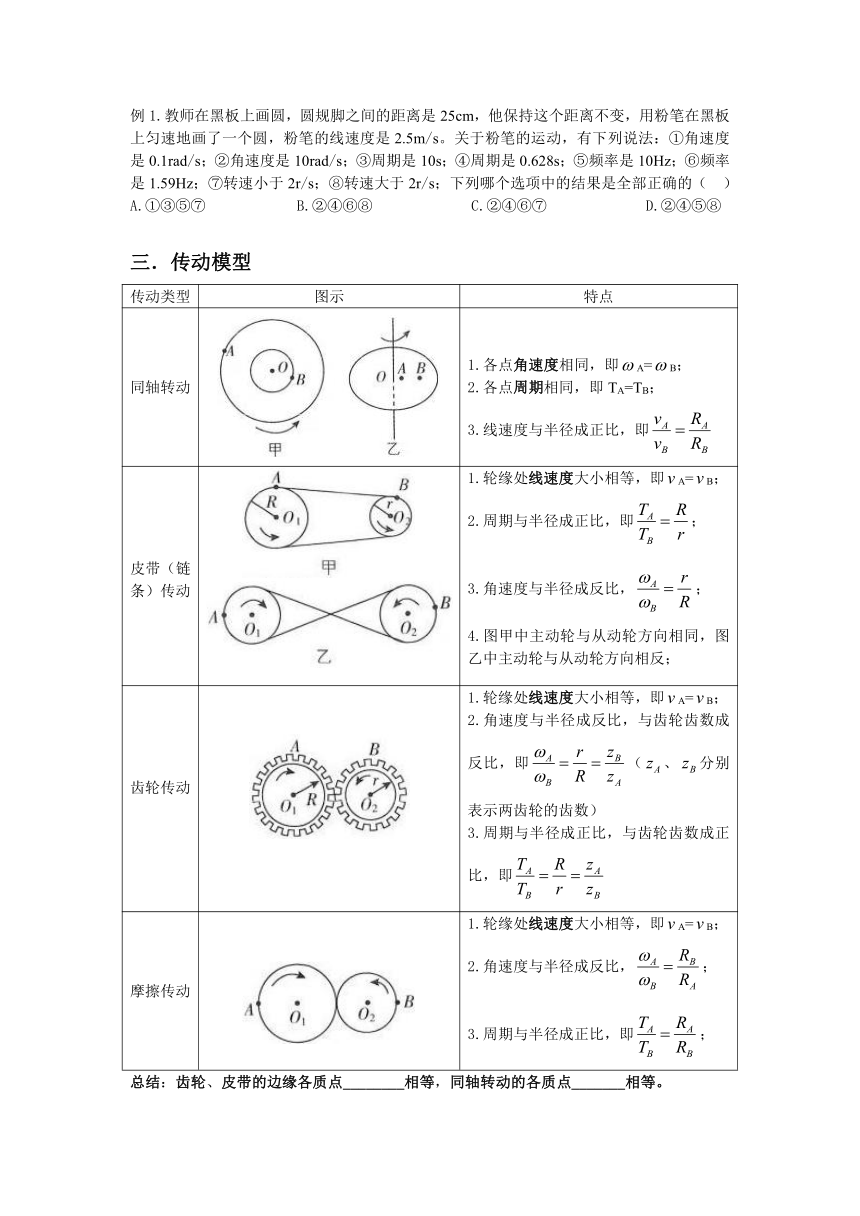
例1.教师在黑板上画圆,圆规脚之间的距离是25cm,他保持这个距离不变,用粉笔在黑板上匀速地画了一个圆,粉笔的线速度是2.5m/s。关于粉笔的运动,有下列说法:①角速度是0.1rad/s;②角速度是10rad/s;③周期是10s;④周期是0.628s;⑤频率是10Hz;⑥频率是1.59Hz;⑦转速小于2r/s;⑧转速大于2r/s;下列哪个选项中的结果是全部正确的( )
A.①③⑤⑦ B.②④⑥⑧ C.②④⑥⑦ D.②④⑤⑧
三.传动模型
传动类型 图示 特点
同轴转动 1.各点角速度相同,即A=B; 2.各点周期相同,即TA=TB; 3.线速度与半径成正比,即
皮带(链条)传动 1.轮缘处线速度大小相等,即A=B; 2.周期与半径成正比,即; 3.角速度与半径成反比,; 4.图甲中主动轮与从动轮方向相同,图乙中主动轮与从动轮方向相反;
齿轮传动 1.轮缘处线速度大小相等,即A=B; 2.角速度与半径成反比,与齿轮齿数成反比,即(、分别表示两齿轮的齿数) 3.周期与半径成正比,与齿轮齿数成正比,即
摩擦传动 1.轮缘处线速度大小相等,即A=B; 2.角速度与半径成反比,; 3.周期与半径成正比,即;
总结:齿轮、皮带的边缘各质点________相等,同轴转动的各质点_______相等。
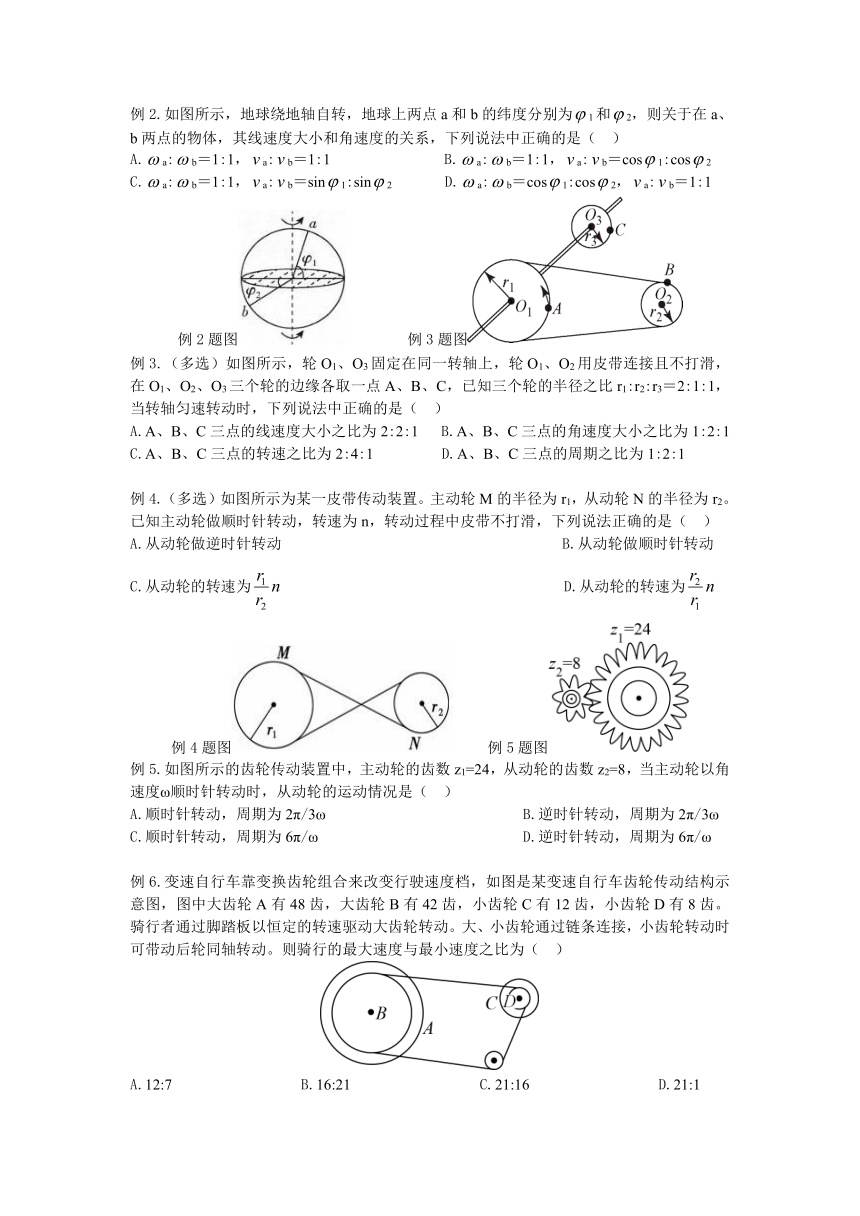
例2.如图所示,地球绕地轴自转,地球上两点a和b的纬度分别为1和2,则关于在a、b两点的物体,其线速度大小和角速度的关系,下列说法中正确的是( )
A.a:b=1:1,a:b=1:1 B.a:b=1:1,a:b=cos1:cos2
C.a:b=1:1,a:b=sin1:sin2 D.a:b=cos1:cos2,a:b=1:1
例2题图 例3题图
例3.(多选)如图所示,轮O1、O3固定在同一转轴上,轮O1、O2用皮带连接且不打滑,在O1、O2、O3三个轮的边缘各取一点A、B、C,已知三个轮的半径之比r1:r2:r3=2:1:1,当转轴匀速转动时,下列说法中正确的是( )
A.A、B、C三点的线速度大小之比为2:2:1 B.A、B、C三点的角速度大小之比为1:2:1
C.A、B、C三点的转速之比为2:4:1 D.A、B、C三点的周期之比为1:2:1
例4.(多选)如图所示为某一皮带传动装置。主动轮M的半径为r1,从动轮N的半径为r2。已知主动轮做顺时针转动,转速为n,转动过程中皮带不打滑,下列说法正确的是( )
A.从动轮做逆时针转动 B.从动轮做顺时针转动
C.从动轮的转速为 D.从动轮的转速为
例4题图 例5题图
例5.如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
A.顺时针转动,周期为2π/3ω B.逆时针转动,周期为2π/3ω
C.顺时针转动,周期为6π/ω D.逆时针转动,周期为6π/ω
例6.变速自行车靠变换齿轮组合来改变行驶速度档,如图是某变速自行车齿轮传动结构示意图,图中大齿轮A有48齿,大齿轮B有42齿,小齿轮C有12齿,小齿轮D有8齿。骑行者通过脚踏板以恒定的转速驱动大齿轮转动。大、小齿轮通过链条连接,小齿轮转动时可带动后轮同轴转动。则骑行的最大速度与最小速度之比为( )
A.12:7 B.16:21 C.21:16 D.21:1
例7.如图所示,甲、乙、丙三个轮子依靠摩擦转动,相互之间不打滑,其半径分别为r1、r2、r3。若甲轮的角速度为ω1,则丙轮的角速度为( )
A. B. C. D.
四.圆周运动的多解问题
1.原因分析:圆周运动具有周期性,该类问题常出现多解问题,有些题目会涉及圆周运动、平抛运动、匀速直线运动等不同运动形式,两种不同的运动规律间必然有一个物理量在起桥梁作用,把两种不同的运动联系起来,这一个物理量常常是“时间”。
2.解题思路:先不考虑周期性,表示出一个周期的情况,在根据运动的周期性,将转过的角度θ再加上2kπ,k的取值视具体情况而定。
例8.如图所示,半径为R的水平圆板绕过中心的竖轴做匀速圆周运动,当半径OB转到某一方向时,在圆板中心正上方h处以平行于OB方向水平抛出一个小球,小球抛出时的速度及圆板转动的角速度为多大时,小球与圆板只碰一次,且相碰点为B
例9.为了测定子弹的飞行速度,在一根水平放置的轴杆上固定着两个薄圆盘A、B,A、B平行且相距2m,轴杆的转速为60r/s,子弹穿过两盘留下两个弹孔a、b,测得两弹孔所在的半径间的夹角为30°,如图所示,则该子弹的速度可能是( )
A.300m/s B.720m/s C.1080m/s D.1440m/s
巩固提升
1.汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长。某国产轿车的车轮半径为30cm,当该型号轿车在高速公路上行驶时,驾驶员面前的速率计的指针指在“120km/h”上,可估算出该车车轮的转速约为( )
A.1000 r/s B.1000 r/h C.1000 r/min D.2000 r/h
2.如图所示是一辆共享单车,A、B、C三点分别为单车轮胎和齿轮外沿上的点,其中RA=2RB=5RC,下列说法中正确的是( )
A.B点与C点的角速度,B=C B.A点与C点的线速度,A=C
C.A点与B点的角速度,2A=5B D.A点与B点的线速度,A=2B
2题图 3题图
3.转笔是一项深受广大学生喜爱的休闲活动,如图所示,长为L的笔绕笔杆上的O点做圆周运动,当笔尖的速度为1时,笔帽的速度为2,则转轴O到笔帽的距离为( )
A. B. C. D.
4.(多选)如图所示,直径为D的薄圆筒绕竖直中心轴线匀速转动。一颗子弹沿筒截面的直径方向从左侧水平射入,经过t时间从右侧射出,发现两弹孔在同一竖直线上。若子弹每次击穿薄圆筒前后水平速度不变,重力加速度为g,则以下说法正确的是( )
A.子弹的初速度大小为 B.两个弹孔的高度差为
C.圆筒转动的角速度可能是 D.圆筒转动的周期可能为4t
5.如图所示,一根长为L的轻杆,O端用光滑的铰链固定,另一端固定着一个小球A,轻杆靠在一个高为h的物块上。若物块与地面间的摩擦不计,则当物块以速度向右运动至轻杆与水平方向夹角为θ时,物块与轻杆的接触点为B,下列说法正确的是( )
A.A的角速度大于B点的角速度 B.A的线速度等于B点的线速度
C.小球A转动的角速度为 D.小球A的线速度大小为
6.如图为一种“滚轮——平盘无极变速器”的示意图,它由固定于主动轴上的平盘和可带动从动轴转动的圆柱形滚轮组成。由于摩擦力的作用,当平盘转动时,滚轮就会跟随转动,如果认为滚轮不会打滑,那么主动轴的转速n1、从动轴的转速n2、滚轮半径r以及滚轮中心距离主动轴轴线的距离之间的关系是( )
A. B. C. D.
6题图 7题图
7.(多选)如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P点等高,且距离P点为L。当飞镖以初速度0垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动。忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
A.飞镖击中P点所需的时间为 B.圆盘的半径可能为
C.圆盘转动角速度的最小值为 D.P点随圆盘转动的线速度大小可能为
8.小明撑一雨伞站在水平地面上,伞边缘点所围圆形的半径为R,现将雨伞绕竖直伞杆以角速度匀速旋转,伞边缘上的水滴落到地面,落点形成一半径为r的圆形,当地重力加速度大小为g,根据以上数据可推知伞边缘距地面的高度为( )
A. B. C. D.
第一讲 圆周运动
一.圆周运动中“匀速”与“非匀速”的理解
1.“匀速”与“非匀速”中“速”指的是速度的 不变,而非速度的 不变。
2.匀速圆周运动是一种非匀变速曲线运动。
二.描述圆周运动快慢的物理量
1.线速度
(1)定义:物体做圆周运动通过的弧长与所用时间的比值定义为线速度。
(2)物理意义:描述质点沿 运动的快慢。
(3)表达式:,其单位是________,其方向为圆周上该点的_________。
(4)线速度也有平均值与瞬时值之分,当△t足够小时,就是瞬时线速度,简称线速度。
(5)线速度是矢量,其方向与轨迹相切。如果物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做 。
2.角速度
(1)定义:质点所在的半径转过的角度和所用时间的比值叫做角速度。
(2)物理意义:描述质点绕 转动的快慢。
(3)表达式:,角速度的单位为______。
(4)匀速圆周运动中角速度大小、方向均不变。
(5)角速度是矢量,方向垂直于转动平面。
3.周期
(1)定义:质点运动一周所用的时间。
(2)表达式:,推导可得。
(3)匀速圆周运动的周期不变。
4.转速(频率)
(1)定义:质点做圆周运动时,单位时间内转过的圈数称为转速,符号是n,其单位为_____。
(2)周期的倒数是频率,符号是f,单位是Hz,当转速的单位取转每秒(r/s)时,频率大小等于转速大小。
(2)表达式:
5.线速度、角速度、周期、转速的关系
例1.教师在黑板上画圆,圆规脚之间的距离是25cm,他保持这个距离不变,用粉笔在黑板上匀速地画了一个圆,粉笔的线速度是2.5m/s。关于粉笔的运动,有下列说法:①角速度是0.1rad/s;②角速度是10rad/s;③周期是10s;④周期是0.628s;⑤频率是10Hz;⑥频率是1.59Hz;⑦转速小于2r/s;⑧转速大于2r/s;下列哪个选项中的结果是全部正确的( )
A.①③⑤⑦ B.②④⑥⑧ C.②④⑥⑦ D.②④⑤⑧
三.传动模型
传动类型 图示 特点
同轴转动 1.各点角速度相同,即A=B; 2.各点周期相同,即TA=TB; 3.线速度与半径成正比,即
皮带(链条)传动 1.轮缘处线速度大小相等,即A=B; 2.周期与半径成正比,即; 3.角速度与半径成反比,; 4.图甲中主动轮与从动轮方向相同,图乙中主动轮与从动轮方向相反;
齿轮传动 1.轮缘处线速度大小相等,即A=B; 2.角速度与半径成反比,与齿轮齿数成反比,即(、分别表示两齿轮的齿数) 3.周期与半径成正比,与齿轮齿数成正比,即
摩擦传动 1.轮缘处线速度大小相等,即A=B; 2.角速度与半径成反比,; 3.周期与半径成正比,即;
总结:齿轮、皮带的边缘各质点________相等,同轴转动的各质点_______相等。
例2.如图所示,地球绕地轴自转,地球上两点a和b的纬度分别为1和2,则关于在a、b两点的物体,其线速度大小和角速度的关系,下列说法中正确的是( )
A.a:b=1:1,a:b=1:1 B.a:b=1:1,a:b=cos1:cos2
C.a:b=1:1,a:b=sin1:sin2 D.a:b=cos1:cos2,a:b=1:1
例2题图 例3题图
例3.(多选)如图所示,轮O1、O3固定在同一转轴上,轮O1、O2用皮带连接且不打滑,在O1、O2、O3三个轮的边缘各取一点A、B、C,已知三个轮的半径之比r1:r2:r3=2:1:1,当转轴匀速转动时,下列说法中正确的是( )
A.A、B、C三点的线速度大小之比为2:2:1 B.A、B、C三点的角速度大小之比为1:2:1
C.A、B、C三点的转速之比为2:4:1 D.A、B、C三点的周期之比为1:2:1
例4.(多选)如图所示为某一皮带传动装置。主动轮M的半径为r1,从动轮N的半径为r2。已知主动轮做顺时针转动,转速为n,转动过程中皮带不打滑,下列说法正确的是( )
A.从动轮做逆时针转动 B.从动轮做顺时针转动
C.从动轮的转速为 D.从动轮的转速为
例4题图 例5题图
例5.如图所示的齿轮传动装置中,主动轮的齿数z1=24,从动轮的齿数z2=8,当主动轮以角速度ω顺时针转动时,从动轮的运动情况是( )
A.顺时针转动,周期为2π/3ω B.逆时针转动,周期为2π/3ω
C.顺时针转动,周期为6π/ω D.逆时针转动,周期为6π/ω
例6.变速自行车靠变换齿轮组合来改变行驶速度档,如图是某变速自行车齿轮传动结构示意图,图中大齿轮A有48齿,大齿轮B有42齿,小齿轮C有12齿,小齿轮D有8齿。骑行者通过脚踏板以恒定的转速驱动大齿轮转动。大、小齿轮通过链条连接,小齿轮转动时可带动后轮同轴转动。则骑行的最大速度与最小速度之比为( )
A.12:7 B.16:21 C.21:16 D.21:1
例7.如图所示,甲、乙、丙三个轮子依靠摩擦转动,相互之间不打滑,其半径分别为r1、r2、r3。若甲轮的角速度为ω1,则丙轮的角速度为( )
A. B. C. D.
四.圆周运动的多解问题
1.原因分析:圆周运动具有周期性,该类问题常出现多解问题,有些题目会涉及圆周运动、平抛运动、匀速直线运动等不同运动形式,两种不同的运动规律间必然有一个物理量在起桥梁作用,把两种不同的运动联系起来,这一个物理量常常是“时间”。
2.解题思路:先不考虑周期性,表示出一个周期的情况,在根据运动的周期性,将转过的角度θ再加上2kπ,k的取值视具体情况而定。
例8.如图所示,半径为R的水平圆板绕过中心的竖轴做匀速圆周运动,当半径OB转到某一方向时,在圆板中心正上方h处以平行于OB方向水平抛出一个小球,小球抛出时的速度及圆板转动的角速度为多大时,小球与圆板只碰一次,且相碰点为B
例9.为了测定子弹的飞行速度,在一根水平放置的轴杆上固定着两个薄圆盘A、B,A、B平行且相距2m,轴杆的转速为60r/s,子弹穿过两盘留下两个弹孔a、b,测得两弹孔所在的半径间的夹角为30°,如图所示,则该子弹的速度可能是( )
A.300m/s B.720m/s C.1080m/s D.1440m/s
巩固提升
1.汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长。某国产轿车的车轮半径为30cm,当该型号轿车在高速公路上行驶时,驾驶员面前的速率计的指针指在“120km/h”上,可估算出该车车轮的转速约为( )
A.1000 r/s B.1000 r/h C.1000 r/min D.2000 r/h
2.如图所示是一辆共享单车,A、B、C三点分别为单车轮胎和齿轮外沿上的点,其中RA=2RB=5RC,下列说法中正确的是( )
A.B点与C点的角速度,B=C B.A点与C点的线速度,A=C
C.A点与B点的角速度,2A=5B D.A点与B点的线速度,A=2B
2题图 3题图
3.转笔是一项深受广大学生喜爱的休闲活动,如图所示,长为L的笔绕笔杆上的O点做圆周运动,当笔尖的速度为1时,笔帽的速度为2,则转轴O到笔帽的距离为( )
A. B. C. D.
4.(多选)如图所示,直径为D的薄圆筒绕竖直中心轴线匀速转动。一颗子弹沿筒截面的直径方向从左侧水平射入,经过t时间从右侧射出,发现两弹孔在同一竖直线上。若子弹每次击穿薄圆筒前后水平速度不变,重力加速度为g,则以下说法正确的是( )
A.子弹的初速度大小为 B.两个弹孔的高度差为
C.圆筒转动的角速度可能是 D.圆筒转动的周期可能为4t
5.如图所示,一根长为L的轻杆,O端用光滑的铰链固定,另一端固定着一个小球A,轻杆靠在一个高为h的物块上。若物块与地面间的摩擦不计,则当物块以速度向右运动至轻杆与水平方向夹角为θ时,物块与轻杆的接触点为B,下列说法正确的是( )
A.A的角速度大于B点的角速度 B.A的线速度等于B点的线速度
C.小球A转动的角速度为 D.小球A的线速度大小为
6.如图为一种“滚轮——平盘无极变速器”的示意图,它由固定于主动轴上的平盘和可带动从动轴转动的圆柱形滚轮组成。由于摩擦力的作用,当平盘转动时,滚轮就会跟随转动,如果认为滚轮不会打滑,那么主动轴的转速n1、从动轴的转速n2、滚轮半径r以及滚轮中心距离主动轴轴线的距离之间的关系是( )
A. B. C. D.
6题图 7题图
7.(多选)如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P点等高,且距离P点为L。当飞镖以初速度0垂直盘面瞄准P点抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动。忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
A.飞镖击中P点所需的时间为 B.圆盘的半径可能为
C.圆盘转动角速度的最小值为 D.P点随圆盘转动的线速度大小可能为
8.小明撑一雨伞站在水平地面上,伞边缘点所围圆形的半径为R,现将雨伞绕竖直伞杆以角速度匀速旋转,伞边缘上的水滴落到地面,落点形成一半径为r的圆形,当地重力加速度大小为g,根据以上数据可推知伞边缘距地面的高度为( )
A. B. C. D.
