新课标A版必修5等差数列(第一课时)浙江
文档属性
| 名称 | 新课标A版必修5等差数列(第一课时)浙江 |
|
|
| 格式 | rar | ||
| 文件大小 | 229.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-25 00:00:00 | ||
图片预览







文档简介
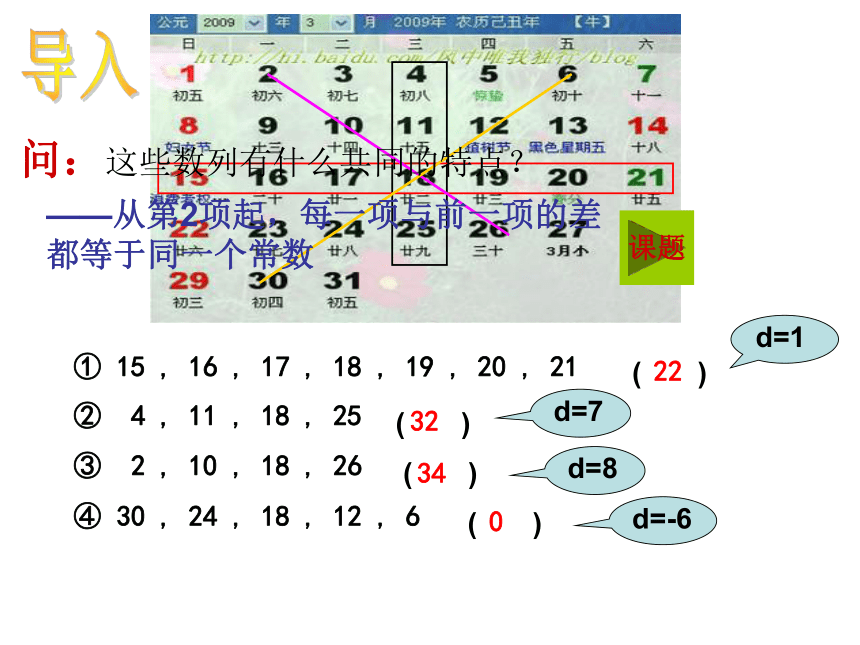
课件18张PPT。① 15 , 16 , 17 , 18 , 19 , 20 , 21 ② 4 , 11 , 18 , 25 ③ 2 , 10 , 18 , 26 ④ 30 , 24 , 18 , 12 , 6( )( )( )( )2232034导入问:这些数列有什么共同的特点?课题——从第2项起,每一项与前一项的差都等于同一个常数2.2.1等差数列主讲人:黄瑶 ——一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一常数,这个数列就叫做等差数列.这个常数叫做等差数列的公差(用字母d表示)注意:1)公差d一定是由后项减前项 3)数学语言(表达式):an-an-1=d (d是常数,n≥2,n∈N*)
2)关键字:“从第2项起”“同一常数”公差可以是正数,负数,也可以为0
想一想:最简单的等差数列有几项?一、等差数列的定义:由三个数a,A,b组成的等差数列可以看成最简单的等差数列。解:这时,A叫做a和b的等差中项。问:此时, a,A,b三者之间满足什么关系式呢?结论:A 叫做 a 与 b 的 等差中项。① 15 , 16 , 17 , 18 , 19 , 20 , 21 ② 4 , 11 , 18 , 25 ③ 2 , 10 , 18 , 26 ④ 30 , 24 , 18 , 12 , 6问:这四个数列的通项公式存在吗?如果存在,又分别是多少?=n+14=7n-3=8n-6=-6n+36 1 , 2 , 3 , 4 , 5 , 6 , 7 二、通项探究问题1:已知等差数列{an}的首项是a1,公差是d(即an-an-1=d),试写出a2,a3,a4,并归纳出它的一个通项公式an(用首项a1及公差d表示)。 等差数列的通项公式的推导1(归纳猜想) n=1时亦适合归纳猜想得解:说明:此公式只是等差数列通项公式的猜想,你能证明吗?累加得…等差数列的通项公式的证明(累加法)返回证:二、通项探究问题1:已知等差数列{an}的首项是a1,公差是d(即an-an-1=d),试写出a2,a3,a4,并归纳出它的一个通项公式an(用首项a1及公差d表示)。 等差数列通项公式:等差数列第二通项公式:问题2:等差数列{ }的第n项 和第m项 有什么关系?an=a1+(n-1)d (n∈N*)三、通项公式的运用1、已知等差数列8,5,2,…求 an及a20(第20项)。解: a1=8, d=5-8=-3∴a20=-49∴an=8+(n-1)·(-3)=-3n+11练习:已知等差数列3,7,11,…
则 an=_______________ a4=_________
a10=__________
an=a1+(n-1)d (n∈N*)4n-11539例题评说:例一:2、已知等差数列中,a20=-49, d=-3 求a1 .解:由a20=a1+(20-1)·(-3)得a1=8an=a1+(n-1)d (n∈N*)3、已知等差数列8,5,2…问-49是第几项?解 :a1=8, d=-3则
an=8+(n-1)·(-3)
-49=8+(n-1)·(-3)
得 n=20。总结:在an=a1+(n-1)d ( n∈N* )中,
有an,a1,n,d 四个量,
已知其中任意3个量即可求出第四个量。思考:如果已知一个等差数列的任意两项,
能否求出an呢?an=a1+(n-1)d (n∈N*)解:由通项公式性质可知, a12=a5+(12-5)d∴ 31=10+7d∴ d=3再由a5=a1+(5-1)d,得 10=a1+12∴ a1=-2 此题解法是利用数学的函数与方程思想,函数与方程思想是数学几个重要思想方法之一,也是高考必考的思想方法,应熟悉并掌握。 某市出租车的计价标准为1.2元/km,起步价为10元,即最初的4km(不含4千米)计费10元,如果某人乘坐该市的出租车去往14km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?例二:答:需要支付车费23.2元令 =11.2,表示4km处的车费,公差d=1.2.
那么,当出租车行至14km处时,n=11,此时需要支付车费解:根据题意,当该市出租车的行程大于或等于4km时,每增加1km,乘客需要支付1.2元。所以,我们可以建立一个等差数列{ }来计算车费。四、课堂小结1、等差数列的定义:an-an-1=d(d是常数,n≥2,n∈N*)an=a1+(n-1)d an=am+(n-m)d3、等差数列的通项公式: (知三求一)
及其推导(归纳猜想、累加法)
、4、等差数列的第二通项公式:2、等差中项:若a,A,b成等差数列,那么A叫做a与b
的等差中项5、建立数学模型解决实际问题GOOD-BYE谢谢!
2)关键字:“从第2项起”“同一常数”公差可以是正数,负数,也可以为0
想一想:最简单的等差数列有几项?一、等差数列的定义:由三个数a,A,b组成的等差数列可以看成最简单的等差数列。解:这时,A叫做a和b的等差中项。问:此时, a,A,b三者之间满足什么关系式呢?结论:A 叫做 a 与 b 的 等差中项。① 15 , 16 , 17 , 18 , 19 , 20 , 21 ② 4 , 11 , 18 , 25 ③ 2 , 10 , 18 , 26 ④ 30 , 24 , 18 , 12 , 6问:这四个数列的通项公式存在吗?如果存在,又分别是多少?=n+14=7n-3=8n-6=-6n+36 1 , 2 , 3 , 4 , 5 , 6 , 7 二、通项探究问题1:已知等差数列{an}的首项是a1,公差是d(即an-an-1=d),试写出a2,a3,a4,并归纳出它的一个通项公式an(用首项a1及公差d表示)。 等差数列的通项公式的推导1(归纳猜想) n=1时亦适合归纳猜想得解:说明:此公式只是等差数列通项公式的猜想,你能证明吗?累加得…等差数列的通项公式的证明(累加法)返回证:二、通项探究问题1:已知等差数列{an}的首项是a1,公差是d(即an-an-1=d),试写出a2,a3,a4,并归纳出它的一个通项公式an(用首项a1及公差d表示)。 等差数列通项公式:等差数列第二通项公式:问题2:等差数列{ }的第n项 和第m项 有什么关系?an=a1+(n-1)d (n∈N*)三、通项公式的运用1、已知等差数列8,5,2,…求 an及a20(第20项)。解: a1=8, d=5-8=-3∴a20=-49∴an=8+(n-1)·(-3)=-3n+11练习:已知等差数列3,7,11,…
则 an=_______________ a4=_________
a10=__________
an=a1+(n-1)d (n∈N*)4n-11539例题评说:例一:2、已知等差数列中,a20=-49, d=-3 求a1 .解:由a20=a1+(20-1)·(-3)得a1=8an=a1+(n-1)d (n∈N*)3、已知等差数列8,5,2…问-49是第几项?解 :a1=8, d=-3则
an=8+(n-1)·(-3)
-49=8+(n-1)·(-3)
得 n=20。总结:在an=a1+(n-1)d ( n∈N* )中,
有an,a1,n,d 四个量,
已知其中任意3个量即可求出第四个量。思考:如果已知一个等差数列的任意两项,
能否求出an呢?an=a1+(n-1)d (n∈N*)解:由通项公式性质可知, a12=a5+(12-5)d∴ 31=10+7d∴ d=3再由a5=a1+(5-1)d,得 10=a1+12∴ a1=-2 此题解法是利用数学的函数与方程思想,函数与方程思想是数学几个重要思想方法之一,也是高考必考的思想方法,应熟悉并掌握。 某市出租车的计价标准为1.2元/km,起步价为10元,即最初的4km(不含4千米)计费10元,如果某人乘坐该市的出租车去往14km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?例二:答:需要支付车费23.2元令 =11.2,表示4km处的车费,公差d=1.2.
那么,当出租车行至14km处时,n=11,此时需要支付车费解:根据题意,当该市出租车的行程大于或等于4km时,每增加1km,乘客需要支付1.2元。所以,我们可以建立一个等差数列{ }来计算车费。四、课堂小结1、等差数列的定义:an-an-1=d(d是常数,n≥2,n∈N*)an=a1+(n-1)d an=am+(n-m)d3、等差数列的通项公式: (知三求一)
及其推导(归纳猜想、累加法)
、4、等差数列的第二通项公式:2、等差中项:若a,A,b成等差数列,那么A叫做a与b
的等差中项5、建立数学模型解决实际问题GOOD-BYE谢谢!
