人教版七年级数学下册第八章《二元一次方程组》章节练习(含解析)
文档属性
| 名称 | 人教版七年级数学下册第八章《二元一次方程组》章节练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 69.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 00:00:00 | ||
图片预览





文档简介
七年级数学下册第八章《二元一次方程组》章节练习
一、单选题(共10小题,每小题3分,满分30分)
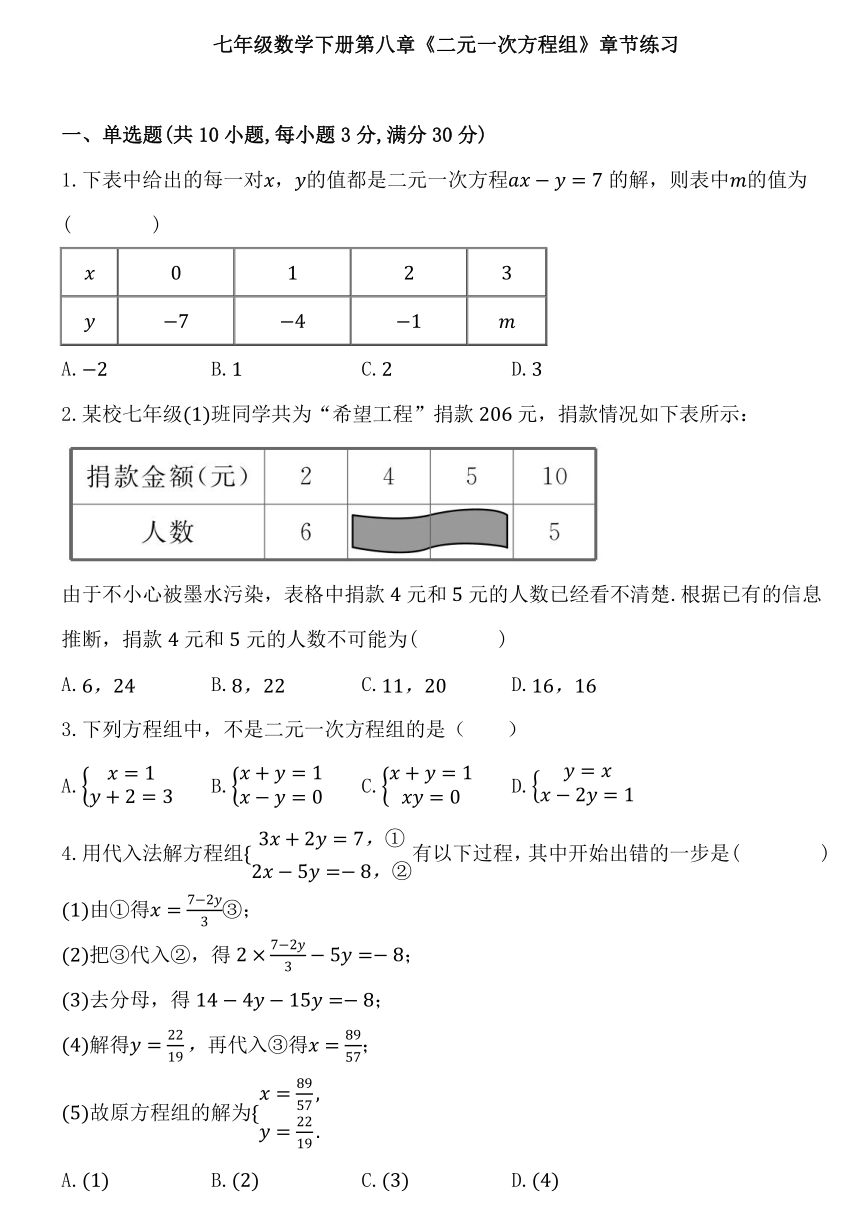
1.下表中给出的每一对,的值都是二元一次方程的解,则表中的值为( )
A. B. C. D.
2.某校七年级班同学共为“希望工程”捐款元,捐款情况如下表所示:
由于不小心被墨水污染,表格中捐款元和元的人数已经看不清楚.根据已有的信息推断,捐款元和元的人数不可能为( )
A. B. C. D.
3.下列方程组中,不是二元一次方程组的是( )
A. B. C. D.
4.用代入法解方程组有以下过程,其中开始出错的一步是( )
由①得③;
把③代入②,得;
去分母,得;
解得再代入③得;
故原方程组的解为
A. B. C. D.
5.用加减法解方程组由②①消去未知数,所得到的一元一次方程是( )
A. B. C. D.
6.已知一个二元一次方程组的解是则这个方程组可能是( )
A. B.
C. D.
7.把一根长为的钢管截成长和长两种规格均有的钢管(损耗忽略不计),不造成浪费的截法共有( )
A.种 B.种 C.种 D.种
8.甲、乙两数之比为:,甲数比乙数的倍小,设甲数为,乙数为,根据题意,所列方程组为( )
A. B. C. D.
9.利用两块完全一样的长方体木块测量一张桌子的高度,首先按如图①所示的方式放置,再交换两木块的位置,按如图②所示的方式放置,测量的数据如图所示,则桌子的高度为( )
A. B. C. D.
10.中央电视台套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
A. B. C. D.
二、填空题(共10小题,每小题3分,满分30分)
11.已知是方程的一组解(,),任写出一组符合题意的、值,则 , .
12.在方程的正整数解中,使的值最小的解是 .
13.某校在一段时间核酸检测过程中,甲班的个男生和个女生的核酸总次数与乙班的个男生和个女生的核酸总次数相等,都是次,已知每人的核酸次数相同,则每人的核酸次数为 次.
14.写出一个解为的二元一次方程:
15.已知关于的方程组若的值为,则 .
16.已知二元一次方程组,则 .
17.若,,则的值是 .
18.如图,,的度数比的度数的两倍少设和的度数分别为那么为求出这两个角的度数可列方程组为 .
19.两地相距甲从地、乙从地同时出发,相向而行,经过相遇,相遇后,甲立即返回地,乙仍向地前进,甲回到地时,乙离地还有则甲的速度为 乙的速度为 .
20.幻方,最早源于我国,古人称之为纵横图,如图所示幻方中,各行、各列及各条对角线上三个数字之和均相等,则图中的值为
三、解答题(共8小题,满分60分)
21.用加减消元法解下列方程组(16分)
(1)
,
(4)
22.解关于,的方程组时,小明把写错,得到错误的解而正确的解是求,,的值(6分)
23.某学校组织学生举行“远足研学”活动,先以每小时千米的速度走平路,后又以每小时千米的速度上坡,共用了小时.原路返回时,以每小时千米的速度下坡,又以每小时千米的速度走平路,共用了小时,则平路和坡路的路程各多少千米?(6分)
24.某种仪器由个部件和个部件配套构成每个工人每天可以生产部件个或者生产部件个,现有工人名,应怎样安排人力才能使每天生产的部件和部件配套?(6分)
25.某厂生产甲、乙两种型号的产品,生产一个甲种产品需时间,铜;生产一个乙种产品需时间,铜.如果生产甲、乙两种产品共用时,共用铜,那么甲、乙两种产品各生产多少个?(6分)
26.如图,宽为的大长方形由个相同的小长方形拼成,求大长方形的面积.(6分)
27.甲地到乙地全程是段上坡、一段平路、一段下坡如果保持上坡每小时走,平路每小时走,下坡每小时走,那么从甲地到乙地需,从乙地到甲地需,求从甲地到乙地时,上坡、平路、下坡的路程分别是多少千米.(7分)
28.一般地,二元一次方程的解有无数个,但是有些二元一次方程的正整数解却只有有限个,如二元一次方程的正整数解只有和两个.
那么,我们如何寻找二元一次方程的正整数解呢?(7分)
不妨以方程为例,首先观察方程各项的特征,发现和分别是偶数和奇数,可以确定必然是奇数,即是奇数,再运用特值法代入尝试,即将,,,…等奇数代入原方程依次求出相应的的值,从而获得的正整数解.
同学们还可以尝试运用列表法来探索二元一次方程的正整数解.
(1)盒子里有若干个大小相同的红球和白球,规定从中摸出一个红球得分,摸出一个白球得分,假设小华摸到个红球和个白球,共得分,请你列出关于,的方程,并写出这个方程符合实际意义的所有的解.
(2)已知的三边,,都是正整数,且的周长为,则符合条件的三角形共有 个.
参考答案
1.C
【解析】由表可知:方程的一个解为
代入方程,得,
解得,即,
当时,,
解得.
故选.
2.B
【解析】设捐款元的人数为捐款元的人数为.
依题意,得
则
所以为的倍数.
因为均为非负整数,
所以
故捐款元和元的人数不可能为.
故选.
3.C
【解析】【分析】方程组中共有两个方程,只含有两个未知数,并且所含未知数的项的次数都是一次的方程组,叫二元一次方程组,根据以上定义逐个判断即可.
【解答】解:、符合二元一次方程组的定义,是二元一次方程组,故本选项错误;
、符合二元一次方程组的定义,是二元一次方程组,故本选项错误;
、是二元二次方程组,不是二元一次方程组,故本选项正确;
、符合二元一次方程组的定义,是二元一次方程组,故本选项错误;
故选.
4.C
【解析】其中开始出错的一步为.
正确步骤:去分母,得
解得再代入③得.
故原方程组的解为
5.A
6.D
【解析】将代入各选项中的方程组检验即可得出结论
7.C
8.D
【解析】设甲数为,乙数为,由甲、乙两数之比为:,得出;甲数比乙数的倍小得出;由此联立方程得出答案即可.
解:设甲数为,乙数为,根据题意得,
.
故选:.
此题考查二元一次方程组的实际运用,注意找出题目蕴含的数量关系.
9.B
【解析】设长方体木块的长为宽为桌子的高为.
由题意,得
两式相加,得
解得.故选.
10.D
【解析】由图可知:2个球体的重量=5个圆柱体的重量,2个正方体的重量=3个圆柱体的重量.
设1个球体重,圆柱重,正方体重
由题意得,
消去可得
即
所以三个球体的重量等于5个正方体的重量.
故选D.
11. ; (答案不唯一)
【解析】把代入方程
可得:
时,有
故答案为:,.(答案不唯一)
12.
【解析】由,得.
又因为均为正整数,
所以必为的整数倍,
则有
其中,使的值最小的解是
13.或(或 或)
【解析】本题主要考查了整数的整除性,根据整除确定、的值是解答本题的关键.
由题意可得,然后再将化成,即,都整除,然后运用列举法可得或,最后分两种情况求得核酸次数即可.
解:每人的核酸次数为次,则:,即
则有:
,都整除,则或,
当时,每人核酸次数为;
当时,每人核酸次数为.
综上,人的核酸次数为或次.
故答案为:或.
14.(答案不唯一)
15.;
16.
【解析】此题考查了解二元一次方程组,本题注意观察方程组中两方程系数之间的关系,利用加减法求出结果.
解:,
①②得:,
则,
故答案为:
方程组中两方程相加,求出的值即可.
17.
【解析】∵,,∴.
把代入中,
得原式
18.
19.;
【解析】设甲的速度为乙的速度为.根据题意,得
解得
所以甲的速度为乙的速度为.
20.
【解析】本题考查了参数方程组,掌握整体代换的方法解参数方程组是解题关键.
空格分别用参数表示,可得等量关系式,进行整体代换进行计算即可.
解:如图,由题意得:
,
,
,
,
,
,
,
故答案为:
21.(1)
①得.③
③+②,得 解得.
将代入①,得.
所以原方程组的解为
(2)
①-②得 解得.
把代入①,得解得.
所以原方程组的解是
(3)
①②得解得.
将代入②,得解得.
所以原方程组的解为
(4)方程组整理,得
①-②,得解得.
将代入②,得解得.
所以原方程组的解为
22.解:把和分别代入得
解得
把代入得,
解得,
所以.
23.解:设平路的路程为千米,坡路的路程为千米.
依题意,得
解得
答:平路的路程为千米,坡路的路程为千米.
24.解:设安排人生产部件,安排人生产部件,由题意,得
,
解得:.
答:安排人生产部件,安排人生产部件,才能使每天生产的部件和部件配套.
【解析】本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,解答时根据条件建立建立反映全题等量关系的两个方程是关键本题时一道配套问题设安排人生产部件,安排人生产部件,就有和,由这两个方程构成方程组,求出其解即可
25.解:设生产甲种产品个,乙种产品个.
根据题意,得
解得
答:生产甲种产品个,乙种产品个.
26.解:设每个小长方形的长是,宽是.
根据题意,得
解得
所以每个小长方形的长是,宽是.
所以大长方形的面积.
答:大长方形的面积是.
27.解:设从甲地到乙地时,上坡、平路、下坡的路程分别是,,.
由题意,得
解得
答:从甲地到乙地时,上坡的路程是,平路的路程是,下坡的路程是.
28.(1)解:依题意得:,
有三个正整数解为或或
(2)
【解析】(2)设,则由,得.
用试值法或者枚举法可得:或或或或或或
所以符合条件的三角形共有个.
故答案是:.
一、单选题(共10小题,每小题3分,满分30分)
1.下表中给出的每一对,的值都是二元一次方程的解,则表中的值为( )
A. B. C. D.
2.某校七年级班同学共为“希望工程”捐款元,捐款情况如下表所示:
由于不小心被墨水污染,表格中捐款元和元的人数已经看不清楚.根据已有的信息推断,捐款元和元的人数不可能为( )
A. B. C. D.
3.下列方程组中,不是二元一次方程组的是( )
A. B. C. D.
4.用代入法解方程组有以下过程,其中开始出错的一步是( )
由①得③;
把③代入②,得;
去分母,得;
解得再代入③得;
故原方程组的解为
A. B. C. D.
5.用加减法解方程组由②①消去未知数,所得到的一元一次方程是( )
A. B. C. D.
6.已知一个二元一次方程组的解是则这个方程组可能是( )
A. B.
C. D.
7.把一根长为的钢管截成长和长两种规格均有的钢管(损耗忽略不计),不造成浪费的截法共有( )
A.种 B.种 C.种 D.种
8.甲、乙两数之比为:,甲数比乙数的倍小,设甲数为,乙数为,根据题意,所列方程组为( )
A. B. C. D.
9.利用两块完全一样的长方体木块测量一张桌子的高度,首先按如图①所示的方式放置,再交换两木块的位置,按如图②所示的方式放置,测量的数据如图所示,则桌子的高度为( )
A. B. C. D.
10.中央电视台套“开心辞典”栏目中,有一期的题目如图所示,两个天平都平衡,则三个球体的重量等于( )个正方体的重量.
A. B. C. D.
二、填空题(共10小题,每小题3分,满分30分)
11.已知是方程的一组解(,),任写出一组符合题意的、值,则 , .
12.在方程的正整数解中,使的值最小的解是 .
13.某校在一段时间核酸检测过程中,甲班的个男生和个女生的核酸总次数与乙班的个男生和个女生的核酸总次数相等,都是次,已知每人的核酸次数相同,则每人的核酸次数为 次.
14.写出一个解为的二元一次方程:
15.已知关于的方程组若的值为,则 .
16.已知二元一次方程组,则 .
17.若,,则的值是 .
18.如图,,的度数比的度数的两倍少设和的度数分别为那么为求出这两个角的度数可列方程组为 .
19.两地相距甲从地、乙从地同时出发,相向而行,经过相遇,相遇后,甲立即返回地,乙仍向地前进,甲回到地时,乙离地还有则甲的速度为 乙的速度为 .
20.幻方,最早源于我国,古人称之为纵横图,如图所示幻方中,各行、各列及各条对角线上三个数字之和均相等,则图中的值为
三、解答题(共8小题,满分60分)
21.用加减消元法解下列方程组(16分)
(1)
,
(4)
22.解关于,的方程组时,小明把写错,得到错误的解而正确的解是求,,的值(6分)
23.某学校组织学生举行“远足研学”活动,先以每小时千米的速度走平路,后又以每小时千米的速度上坡,共用了小时.原路返回时,以每小时千米的速度下坡,又以每小时千米的速度走平路,共用了小时,则平路和坡路的路程各多少千米?(6分)
24.某种仪器由个部件和个部件配套构成每个工人每天可以生产部件个或者生产部件个,现有工人名,应怎样安排人力才能使每天生产的部件和部件配套?(6分)
25.某厂生产甲、乙两种型号的产品,生产一个甲种产品需时间,铜;生产一个乙种产品需时间,铜.如果生产甲、乙两种产品共用时,共用铜,那么甲、乙两种产品各生产多少个?(6分)
26.如图,宽为的大长方形由个相同的小长方形拼成,求大长方形的面积.(6分)
27.甲地到乙地全程是段上坡、一段平路、一段下坡如果保持上坡每小时走,平路每小时走,下坡每小时走,那么从甲地到乙地需,从乙地到甲地需,求从甲地到乙地时,上坡、平路、下坡的路程分别是多少千米.(7分)
28.一般地,二元一次方程的解有无数个,但是有些二元一次方程的正整数解却只有有限个,如二元一次方程的正整数解只有和两个.
那么,我们如何寻找二元一次方程的正整数解呢?(7分)
不妨以方程为例,首先观察方程各项的特征,发现和分别是偶数和奇数,可以确定必然是奇数,即是奇数,再运用特值法代入尝试,即将,,,…等奇数代入原方程依次求出相应的的值,从而获得的正整数解.
同学们还可以尝试运用列表法来探索二元一次方程的正整数解.
(1)盒子里有若干个大小相同的红球和白球,规定从中摸出一个红球得分,摸出一个白球得分,假设小华摸到个红球和个白球,共得分,请你列出关于,的方程,并写出这个方程符合实际意义的所有的解.
(2)已知的三边,,都是正整数,且的周长为,则符合条件的三角形共有 个.
参考答案
1.C
【解析】由表可知:方程的一个解为
代入方程,得,
解得,即,
当时,,
解得.
故选.
2.B
【解析】设捐款元的人数为捐款元的人数为.
依题意,得
则
所以为的倍数.
因为均为非负整数,
所以
故捐款元和元的人数不可能为.
故选.
3.C
【解析】【分析】方程组中共有两个方程,只含有两个未知数,并且所含未知数的项的次数都是一次的方程组,叫二元一次方程组,根据以上定义逐个判断即可.
【解答】解:、符合二元一次方程组的定义,是二元一次方程组,故本选项错误;
、符合二元一次方程组的定义,是二元一次方程组,故本选项错误;
、是二元二次方程组,不是二元一次方程组,故本选项正确;
、符合二元一次方程组的定义,是二元一次方程组,故本选项错误;
故选.
4.C
【解析】其中开始出错的一步为.
正确步骤:去分母,得
解得再代入③得.
故原方程组的解为
5.A
6.D
【解析】将代入各选项中的方程组检验即可得出结论
7.C
8.D
【解析】设甲数为,乙数为,由甲、乙两数之比为:,得出;甲数比乙数的倍小得出;由此联立方程得出答案即可.
解:设甲数为,乙数为,根据题意得,
.
故选:.
此题考查二元一次方程组的实际运用,注意找出题目蕴含的数量关系.
9.B
【解析】设长方体木块的长为宽为桌子的高为.
由题意,得
两式相加,得
解得.故选.
10.D
【解析】由图可知:2个球体的重量=5个圆柱体的重量,2个正方体的重量=3个圆柱体的重量.
设1个球体重,圆柱重,正方体重
由题意得,
消去可得
即
所以三个球体的重量等于5个正方体的重量.
故选D.
11. ; (答案不唯一)
【解析】把代入方程
可得:
时,有
故答案为:,.(答案不唯一)
12.
【解析】由,得.
又因为均为正整数,
所以必为的整数倍,
则有
其中,使的值最小的解是
13.或(或 或)
【解析】本题主要考查了整数的整除性,根据整除确定、的值是解答本题的关键.
由题意可得,然后再将化成,即,都整除,然后运用列举法可得或,最后分两种情况求得核酸次数即可.
解:每人的核酸次数为次,则:,即
则有:
,都整除,则或,
当时,每人核酸次数为;
当时,每人核酸次数为.
综上,人的核酸次数为或次.
故答案为:或.
14.(答案不唯一)
15.;
16.
【解析】此题考查了解二元一次方程组,本题注意观察方程组中两方程系数之间的关系,利用加减法求出结果.
解:,
①②得:,
则,
故答案为:
方程组中两方程相加,求出的值即可.
17.
【解析】∵,,∴.
把代入中,
得原式
18.
19.;
【解析】设甲的速度为乙的速度为.根据题意,得
解得
所以甲的速度为乙的速度为.
20.
【解析】本题考查了参数方程组,掌握整体代换的方法解参数方程组是解题关键.
空格分别用参数表示,可得等量关系式,进行整体代换进行计算即可.
解:如图,由题意得:
,
,
,
,
,
,
,
故答案为:
21.(1)
①得.③
③+②,得 解得.
将代入①,得.
所以原方程组的解为
(2)
①-②得 解得.
把代入①,得解得.
所以原方程组的解是
(3)
①②得解得.
将代入②,得解得.
所以原方程组的解为
(4)方程组整理,得
①-②,得解得.
将代入②,得解得.
所以原方程组的解为
22.解:把和分别代入得
解得
把代入得,
解得,
所以.
23.解:设平路的路程为千米,坡路的路程为千米.
依题意,得
解得
答:平路的路程为千米,坡路的路程为千米.
24.解:设安排人生产部件,安排人生产部件,由题意,得
,
解得:.
答:安排人生产部件,安排人生产部件,才能使每天生产的部件和部件配套.
【解析】本题考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,解答时根据条件建立建立反映全题等量关系的两个方程是关键本题时一道配套问题设安排人生产部件,安排人生产部件,就有和,由这两个方程构成方程组,求出其解即可
25.解:设生产甲种产品个,乙种产品个.
根据题意,得
解得
答:生产甲种产品个,乙种产品个.
26.解:设每个小长方形的长是,宽是.
根据题意,得
解得
所以每个小长方形的长是,宽是.
所以大长方形的面积.
答:大长方形的面积是.
27.解:设从甲地到乙地时,上坡、平路、下坡的路程分别是,,.
由题意,得
解得
答:从甲地到乙地时,上坡的路程是,平路的路程是,下坡的路程是.
28.(1)解:依题意得:,
有三个正整数解为或或
(2)
【解析】(2)设,则由,得.
用试值法或者枚举法可得:或或或或或或
所以符合条件的三角形共有个.
故答案是:.
