应用题思维训练篇 圆柱与圆锥(含答案)六年级下册青岛版
文档属性
| 名称 | 应用题思维训练篇 圆柱与圆锥(含答案)六年级下册青岛版 |  | |
| 格式 | docx | ||
| 文件大小 | 403.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 16:03:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
应用题思维训练篇:圆柱与圆锥-六年级下册青岛版
1.把棱长为3分米的正方体木块,加工成最大的圆锥体状木块.求加工成的圆锥形木块的体积.
2.底面半径是6厘米的圆柱体容器与底面半径9厘米的圆锥体容器高相等,现把圆锥体容器装满水倒入圆柱内,水深比容器的低1.5厘米.圆柱体容器深多少厘米?
3.一个圆锥形沙堆,底面周长为18.84米,高1米,这个圆锥形沙堆的体积是多少?
4.在一个底面半径是10cm的圆柱形水桶中装水,水中放一个底面半径是5cm的圆锥形铅锤,铅锤全部淹没,取出铅锤后桶面水面下降2cm,求铅锤的高.
5.将一个底面半径为20厘米、高27厘米的圆锥形铝块,和一个底面半径为30厘米、高20厘米的圆柱形铝块,熔铸成一底面半径为15厘米的圆柱形铝块,求这个圆柱形铝块的高?
6.张磬宇的爸爸用一个棱长6厘米的正方体木块削成一个最大的圆锥体玩具给她玩,削成的圆锥的体积是多少立方厘米?
7.用铁皮制作12节圆柱形通风管,每节通风管的底面直径是8分米,长30分米,至少需要多少平方米的铁皮?(得数保留整数)
8.某剧院大厅内有8根同样的圆柱形立柱,每根高5m,底面直径为40cm。
(1)若给这8根立柱围上装饰板,至少需要多少平方米装饰板?
(2)若给这8根立柱都刷上油漆,如果每千克油漆可刷4.5 m2,大约需要多少千克油漆?(结果保留一位小数)
9.在一个棱长为4厘米的正方体上面的中心,挖去一个底面半径为1厘米、高2厘米的圆柱,求所得物体的表面积。
10.一个圆柱,已知高每增加1厘米,它的侧面积就增加31.4平方厘米。如果高是16厘米,那么它的表面积是多少平方厘米?(π值取3.14)
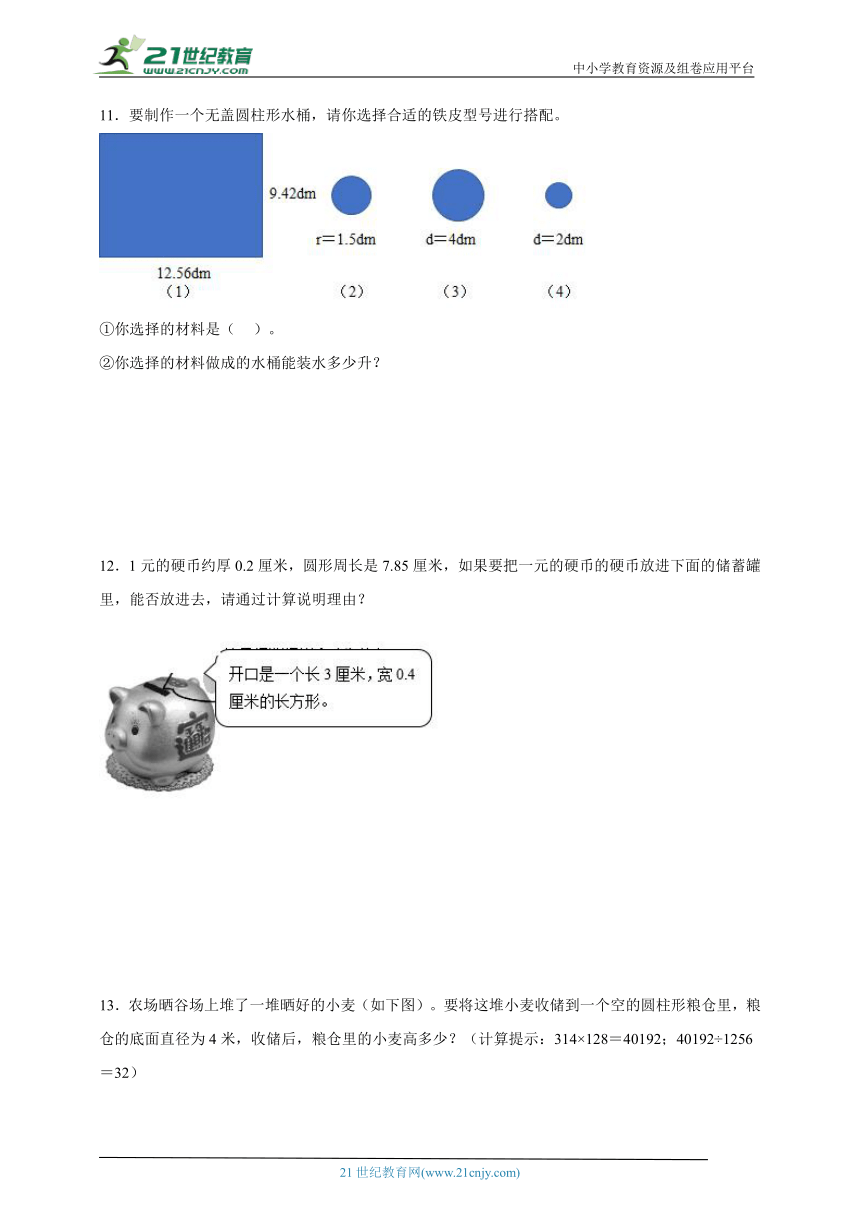
11.要制作一个无盖圆柱形水桶,请你选择合适的铁皮型号进行搭配。
①你选择的材料是( )。
②你选择的材料做成的水桶能装水多少升?
12.1元的硬币约厚0.2厘米,圆形周长是7.85厘米,如果要把一元的硬币的硬币放进下面的储蓄罐里,能否放进去,请通过计算说明理由?
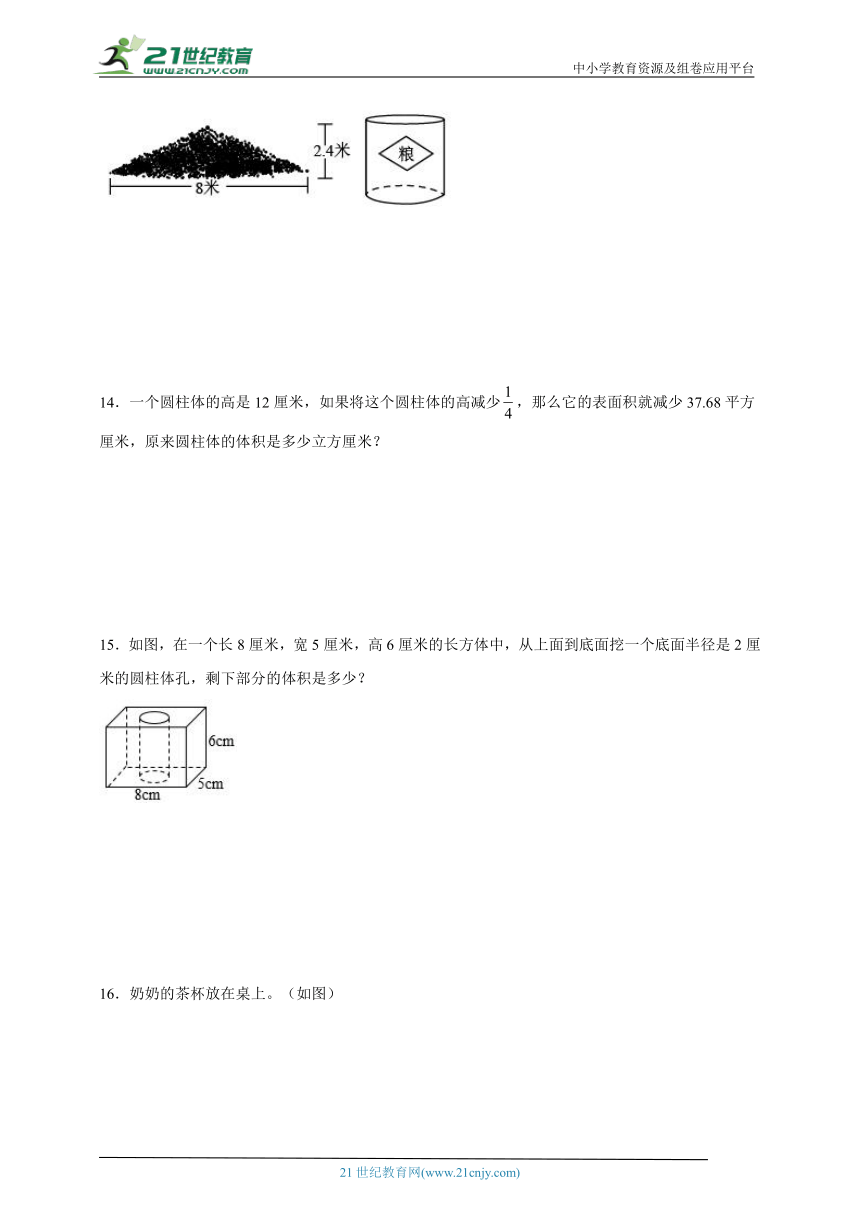
13.农场晒谷场上堆了一堆晒好的小麦(如下图)。要将这堆小麦收储到一个空的圆柱形粮仓里,粮仓的底面直径为4米,收储后,粮仓里的小麦高多少?(计算提示:314×128=40192;40192÷1256=32)
14.一个圆柱体的高是12厘米,如果将这个圆柱体的高减少,那么它的表面积就减少37.68平方厘米,原来圆柱体的体积是多少立方厘米?
15.如图,在一个长8厘米,宽5厘米,高6厘米的长方体中,从上面到底面挖一个底面半径是2厘米的圆柱体孔,剩下部分的体积是多少?
16.奶奶的茶杯放在桌上。(如图)
(1)这只茶杯占桌面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带是妈妈怕烫伤奶奶的手特意贴上的,这条装饰带宽5厘米,它的面积至少有多少平方厘米?(接头处忽略不计)
(3)如果把0.5升的水倒入茶杯,能装满吗?(茶杯壁的厚度不计)
17.图中所示图形是一个底面直径为30厘米的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为8厘米,高12厘米的一个圆锥体铅锤,水面刚好盖住铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π=3.14结果保留两位小数)
18.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
19.烤烟育苗大棚长20米,横截面是一个半径2米的半圆,问制作这样一个育苗大棚需要多少平方米的塑料薄膜?
20.(1)一个会议大厅内的立柱如下图所示,它是由圆柱和底座组成的。要将立柱漆上红色油漆,要漆多少平方米?(上、下底面不漆)
(2)如果这个大厅内有12根这样的立柱,每平方米需要油漆0.2kg,一共需要油漆多少千克?(得数保留三位小数)
21.长方体纸盒中装了4筒羽毛球(如图),已知每筒羽毛球的形状为圆柱形,底面半径为4.5cm,高为45cm,这个纸盒的长、宽、高至少是多少厘米?
22.在学校植物园的周围修一道围墙,原计划用土石60m3。后来多开了一个厚度为24cm,直径为2m的月亮门(如图),减少了土石的用量。实际用了多少立方米土石?
23.下图是底面半径为5厘米的圆柱体从中间斜着截去一段后所得,那么它的体积是多少立方厘米
参考答案:
1.7.065立方分米
【详解】试题分析:在正方体木块中,要加工成最大的圆锥体状木块,圆锥的底面就是在正方体底面中最大的圆,圆锥的高,就是正方体的高,圆锥的底面积、高已知,体积即可求.
解:由题意知,要加工成最大的圆锥体状木块,圆锥的底面就是在正方体底面中最大的圆,即直径是3分米的圆;
r=d÷2=3÷2=1.5(分米);
V锥=πr2h,
=×3.14×1.52×3,
=×3.14×2.25×3,
=7.065(立方分米);
答:加工成的圆锥体状木块的体积为7.065立方分米.
点评:此题考查了如何在一个正方体中削出一个最大的圆锥.
2.30厘米
【详解】试题分析:圆柱的体积公式v=sh,圆锥的体积公式v=sh,两个容器底面半径的比是6:9,它们的底面积的比是36:81,已知两个容器的高相等,由此求出圆锥与圆柱体积的比;求出圆锥的底面积占圆柱底面积的几分之几,又知道现把圆锥体容器装满水倒入圆柱内,水深比容器的低1.5厘米.根据已知比一个数少几分之几的数是多少,求这个数,用除法解答.
解:1.5÷[﹣(×3.14×92)÷(3.14×62)]
=1.5÷[﹣(×3.14×81)÷(3.14×36)]
=1.5÷[﹣(3.14×27)÷(3.14×36)]
=1.5÷[﹣]
=1.5÷
=1.5×20
=30(厘米);
答:圆柱体容器深30厘米.
点评:此题解答是把圆柱体容器的容积看作单位“1”,根据两个容器的高相等,得出圆锥与圆柱体积的比;求出圆锥的底面积占圆柱底面积的几分之几,再已知比一个数少几分之几的数是多少,求这个数,进行解答即可.
3.9.42立方米
【详解】试题分析:沙堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,问题得解.
解:×3.14×(18.84÷3.14÷2)2×1,
=×3.14×32×1,
=3.14×3,
=9.42(立方米);
答:这个圆锥形沙堆的体积是9.42立方米.
点评:此题主要考查圆锥的体积计算公式V=πr2h,运用公式计算时不要漏乘.
4.24cm
【详解】试题分析:根据题意知道圆柱形水桶的水面下降的2cm的水的体积就是圆锥形铅块的体积,由此再根据圆锥的体积公式的变形,h=3V÷s,即可求出铅锥的高.
解:圆锥形铅锥的体积是:
3.14×102×2,
=314×2,
=628(cm3),
铅锥的高是:628×3÷(3.14×52),
=1884÷78.5,
=24(cm),
答:铅锥的高是24cm.
点评:此题主要考查了圆柱与圆锥的体积公式的灵活应用.
5.96厘米
【分析】首先要明确铝块无论被压成什么形状,它的体积是不变的,因此可以分别求出两块铝块的体积,也就等于知道了圆柱形铝块的体积,从而利用圆柱体的体积公式即可求出圆柱形铝块的高。
【详解】(×3.14×202×27+3.14×302×20)÷(3.14×152),
=(3.14×400×9+3.14×900×20)÷(3.14×225),
=(1256×9+2826×20)÷706.5,
=(11304+56520)÷706.5,
=67824÷706.5,
=96(厘米);
答:这个圆的高是96厘米。
6.56.52立方厘米
【详解】试题分析:把一个正方体加工成一个最大的圆锥,关键弄清圆锥的底面直径等于正方体的棱长,圆锥的高也等于正方体的棱长,由此解答.
解:3.14×(6÷2)2×6×,
=3.14×9×6×,
=56.52(立方厘米);
答:削成的圆锥的体积是56.52立方厘米.
点评:此题考查了圆锥的体积计算,以及应用圆锥的体积计算方法解决实际问题.
7.91平方米
【详解】略
8.(1) 50.24m2
(2) 11.2kg
【详解】(1)40 cm=0.4 m
3.14×0.4×5×8=50.24(m2)
答:至少需要50.24 m2装饰板。
(2)50.24÷4.5≈11.2(kg)
答:大约需要11.2 kg油漆。
9.108.56平方厘米
【分析】根据题意可知,物体的表面积=正方体的表面积+圆柱的侧面积,其中圆柱的侧面积=底面周长×高,据此解答。
【详解】
=96+12.56
=108.56(平方厘米)
答:所得物体的表面积是108.56平方厘米。
【点睛】此题考查了组合体表面积的计算,明确挖去一个小圆柱体减少一个圆柱底面的同时又增加了一个圆柱底面,所以只是增加了一个圆柱侧面。
10.659.4平方厘米
【分析】此题先利用侧面积公式:,求出底面半径,根据底面积公式:求出底面积,最后根据圆柱的表面积=侧面积+两个底面积,可求出圆柱的表面积。
【详解】底面半径:31.4÷1÷3.14÷2
=10÷2
=5(厘米)
31.4×16+5×3.14×2
=502.4+157
=659.4(平方厘米)
答:它的表面积是659.4平方厘米。
【点睛】此题主要考查圆柱的表面积的计算方法,根据已知条件,灵活运用侧面积公式以及底面积公式解答。
11.①(1)和(3)
②118.3152升
【分析】①用长方形的长围成一个圆,求出直径,再用长方形的宽,围成一个圆,求出直径,进而求出和那个型号搭配,即可解答;
②再根据圆柱体的体积公式:底面积×高,代入数据,即可解答。
【详解】①12.56÷3.14=4(dm)
9.42÷3.14=3(dm)
直径是4dm,只用图(1)和(3)搭配做成一个无盖水桶。
②3.14×(4÷2)2×9.42
=3.14×22×9.42
=3.14×4×9.42
=12.56×9.42
=118.3152(升)
答:水桶能装水118.3152升。
【点睛】本题考查圆柱体的特征以及圆柱体的体积公式的应用。
12.能;见详解
【分析】根据圆的周长公式,求出圆的直径,用直径与开口的长、厚度与开口的宽比较即可。
【详解】(厘米)
2.5<3
0.2<0.4
答:能放进去。
【点睛】本题主要考查圆柱的特征,注意圆柱的直径与厚度有一项大于开口处就不能放进去。
13.3.2米
【分析】根据圆锥的体积公式:V=πr2h求出这堆小麦的体积,再用这堆小麦的体积除以圆柱的底面积求出粮仓里的小麦高。
【详解】×3.14×(8÷2)2×2.4÷[3.14×(4÷2)2]
=3.14×16×0.8÷[3.14×4]
=3.14×12.8÷12.56
=40.192÷12.56
=3.2(米)
答:粮仓里的小麦高是3.2米。
【点睛】考查了圆柱的体积和圆锥的体积,计算时要认真。
14.150.72立方厘米
【分析】高减少厘米后圆柱的表面积减少37.68平方厘米,先求减少的圆柱的高,用12×=3(厘米),表面积减少的是3厘米的侧面积,用37.68除以3求出底面周长,用底面周长除以圆周率除以3求出底面半径,然后根据圆柱的体积公式:v=sh,把数据代入公式解答。
【详解】减少的圆柱的高:12×=3(厘米),
底面半径是:
37.68÷3÷3.14÷2
=12.56÷3.14÷2
=2(厘米)
原来的体积是:
3.14×22×12
=3.14×4×12
=150.72(立方厘米)
答:原来体积是150.72立方厘米。
【点睛】抓住切割特点,得出减少的表面积是减少的圆柱部分的侧面积,从而求出底面半径是解决本题的关键。
15.164.64立方厘米
【分析】由题目可知,剩下部分的体积=长方体的体积-圆柱的体积;根据长方体的体积公式:长×宽×高;圆柱的体积公式:V=πr2h,把数代入即可求解。
【详解】8×5×6-3.14×2×2×6
=240-75.36
=164.64(立方厘米)
答:剩下部分的体积是164.64立方厘米。
【点睛】本题主要考查长方体以及圆柱的体积公式,熟练掌握它们的体积公式并灵活运用。
16.(1)平方厘米;
(2)平方厘米;
(3)不能
【分析】(1)占桌面的面积也就是圆柱的底面积,根据圆的面积S=πr2,代入数据计算即可。
(2)装饰带的面积=底面周长×宽度;
(3)根据圆柱的体积V=πr2h,求出茶杯的容积与0.5升比较即可。
【详解】(1)
=9×3.14
=28.26(平方厘米)
答:这只茶杯占桌面的大小是28.26平方厘米。
(2)
=3.14×30
=94.2(平方厘米)
答:面积至少有平方厘米。
(3)
=3.14×9×15
=28.26×15
=423.9(立方厘米)
423.9立方厘米=0.4239升
答:不能装满。
【点睛】此题考查了圆柱体的相关应用,明确圆柱的体积和侧面积计算公式,并能灵活运用是解题关键。
17.0.28厘米
【分析】根据圆锥的体积公式:V=πr2h,求出圆锥体铅锤的体积,用圆锥体铅锤的体积除以圆柱形玻璃杯的底面积即可。
【详解】3.14×(8÷2)2×12×÷[3.14×(30÷2)2]
=3.14×16×12×÷[3.14×225]
=50.24×12×÷706.5
=602.88×÷706.5
=200.96÷706.5
≈0.28(厘米)
答:杯里的水大约下降0.28厘米。
【点睛】此题主要考查圆锥体积公式和圆柱体的体积公式的灵活运用,关键是熟记公式。
18.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
【点睛】本题考查学生的空间想象能力,分析底面和背面也需要和正面看到一样多的丝带。
19.平方米
【详解】2×2π÷2×20=40π(平方米)
20.(1) 3.70635m2
(2) 8.895kg
【详解】(1)30 cm=0.3 m 20 cm=0.2 m
40 cm=0.4 m 0.3÷2=0.15(m)
3.14×0.3×3.5+0.2×0.4×4+0.4×0.4-3.14×0.152=3.70635(m2)
答:要漆3.70635 m2。
(2)3.70635×12×0.2≈8.895(kg)
答:一共需要油漆约8.895 kg。
21.45cm,18cm,18cm
【详解】4.5×2×2=18(cm)
答:这个纸盒的长至少是45 cm,宽至少是18 cm,高至少是18 cm。
22.59.2464m3
【分析】实际用土石量=原计划土石量-月亮门体积,月亮门是一个圆柱形,据此可得。
【详解】2÷2=1(m)
24 cm=0.24 m
60-3.14×12×0.24=59.2464(m3)
答:实际用了59.2464 m3土石。
【点睛】注意圆柱的体积计算方法。
23.628立方厘米
【详解】可以用2个相同图形倒扣在一起,形成一个大圆柱体,52×3.14×(6+10)=1256(立方厘米)
1256÷2=628(立方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
应用题思维训练篇:圆柱与圆锥-六年级下册青岛版
1.把棱长为3分米的正方体木块,加工成最大的圆锥体状木块.求加工成的圆锥形木块的体积.
2.底面半径是6厘米的圆柱体容器与底面半径9厘米的圆锥体容器高相等,现把圆锥体容器装满水倒入圆柱内,水深比容器的低1.5厘米.圆柱体容器深多少厘米?
3.一个圆锥形沙堆,底面周长为18.84米,高1米,这个圆锥形沙堆的体积是多少?
4.在一个底面半径是10cm的圆柱形水桶中装水,水中放一个底面半径是5cm的圆锥形铅锤,铅锤全部淹没,取出铅锤后桶面水面下降2cm,求铅锤的高.
5.将一个底面半径为20厘米、高27厘米的圆锥形铝块,和一个底面半径为30厘米、高20厘米的圆柱形铝块,熔铸成一底面半径为15厘米的圆柱形铝块,求这个圆柱形铝块的高?
6.张磬宇的爸爸用一个棱长6厘米的正方体木块削成一个最大的圆锥体玩具给她玩,削成的圆锥的体积是多少立方厘米?
7.用铁皮制作12节圆柱形通风管,每节通风管的底面直径是8分米,长30分米,至少需要多少平方米的铁皮?(得数保留整数)
8.某剧院大厅内有8根同样的圆柱形立柱,每根高5m,底面直径为40cm。
(1)若给这8根立柱围上装饰板,至少需要多少平方米装饰板?
(2)若给这8根立柱都刷上油漆,如果每千克油漆可刷4.5 m2,大约需要多少千克油漆?(结果保留一位小数)
9.在一个棱长为4厘米的正方体上面的中心,挖去一个底面半径为1厘米、高2厘米的圆柱,求所得物体的表面积。
10.一个圆柱,已知高每增加1厘米,它的侧面积就增加31.4平方厘米。如果高是16厘米,那么它的表面积是多少平方厘米?(π值取3.14)
11.要制作一个无盖圆柱形水桶,请你选择合适的铁皮型号进行搭配。
①你选择的材料是( )。
②你选择的材料做成的水桶能装水多少升?
12.1元的硬币约厚0.2厘米,圆形周长是7.85厘米,如果要把一元的硬币的硬币放进下面的储蓄罐里,能否放进去,请通过计算说明理由?
13.农场晒谷场上堆了一堆晒好的小麦(如下图)。要将这堆小麦收储到一个空的圆柱形粮仓里,粮仓的底面直径为4米,收储后,粮仓里的小麦高多少?(计算提示:314×128=40192;40192÷1256=32)
14.一个圆柱体的高是12厘米,如果将这个圆柱体的高减少,那么它的表面积就减少37.68平方厘米,原来圆柱体的体积是多少立方厘米?
15.如图,在一个长8厘米,宽5厘米,高6厘米的长方体中,从上面到底面挖一个底面半径是2厘米的圆柱体孔,剩下部分的体积是多少?
16.奶奶的茶杯放在桌上。(如图)
(1)这只茶杯占桌面的大小是多少平方厘米?
(2)茶杯中部的一圈装饰带是妈妈怕烫伤奶奶的手特意贴上的,这条装饰带宽5厘米,它的面积至少有多少平方厘米?(接头处忽略不计)
(3)如果把0.5升的水倒入茶杯,能装满吗?(茶杯壁的厚度不计)
17.图中所示图形是一个底面直径为30厘米的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为8厘米,高12厘米的一个圆锥体铅锤,水面刚好盖住铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π=3.14结果保留两位小数)
18.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
19.烤烟育苗大棚长20米,横截面是一个半径2米的半圆,问制作这样一个育苗大棚需要多少平方米的塑料薄膜?
20.(1)一个会议大厅内的立柱如下图所示,它是由圆柱和底座组成的。要将立柱漆上红色油漆,要漆多少平方米?(上、下底面不漆)
(2)如果这个大厅内有12根这样的立柱,每平方米需要油漆0.2kg,一共需要油漆多少千克?(得数保留三位小数)
21.长方体纸盒中装了4筒羽毛球(如图),已知每筒羽毛球的形状为圆柱形,底面半径为4.5cm,高为45cm,这个纸盒的长、宽、高至少是多少厘米?
22.在学校植物园的周围修一道围墙,原计划用土石60m3。后来多开了一个厚度为24cm,直径为2m的月亮门(如图),减少了土石的用量。实际用了多少立方米土石?
23.下图是底面半径为5厘米的圆柱体从中间斜着截去一段后所得,那么它的体积是多少立方厘米
参考答案:
1.7.065立方分米
【详解】试题分析:在正方体木块中,要加工成最大的圆锥体状木块,圆锥的底面就是在正方体底面中最大的圆,圆锥的高,就是正方体的高,圆锥的底面积、高已知,体积即可求.
解:由题意知,要加工成最大的圆锥体状木块,圆锥的底面就是在正方体底面中最大的圆,即直径是3分米的圆;
r=d÷2=3÷2=1.5(分米);
V锥=πr2h,
=×3.14×1.52×3,
=×3.14×2.25×3,
=7.065(立方分米);
答:加工成的圆锥体状木块的体积为7.065立方分米.
点评:此题考查了如何在一个正方体中削出一个最大的圆锥.
2.30厘米
【详解】试题分析:圆柱的体积公式v=sh,圆锥的体积公式v=sh,两个容器底面半径的比是6:9,它们的底面积的比是36:81,已知两个容器的高相等,由此求出圆锥与圆柱体积的比;求出圆锥的底面积占圆柱底面积的几分之几,又知道现把圆锥体容器装满水倒入圆柱内,水深比容器的低1.5厘米.根据已知比一个数少几分之几的数是多少,求这个数,用除法解答.
解:1.5÷[﹣(×3.14×92)÷(3.14×62)]
=1.5÷[﹣(×3.14×81)÷(3.14×36)]
=1.5÷[﹣(3.14×27)÷(3.14×36)]
=1.5÷[﹣]
=1.5÷
=1.5×20
=30(厘米);
答:圆柱体容器深30厘米.
点评:此题解答是把圆柱体容器的容积看作单位“1”,根据两个容器的高相等,得出圆锥与圆柱体积的比;求出圆锥的底面积占圆柱底面积的几分之几,再已知比一个数少几分之几的数是多少,求这个数,进行解答即可.
3.9.42立方米
【详解】试题分析:沙堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,问题得解.
解:×3.14×(18.84÷3.14÷2)2×1,
=×3.14×32×1,
=3.14×3,
=9.42(立方米);
答:这个圆锥形沙堆的体积是9.42立方米.
点评:此题主要考查圆锥的体积计算公式V=πr2h,运用公式计算时不要漏乘.
4.24cm
【详解】试题分析:根据题意知道圆柱形水桶的水面下降的2cm的水的体积就是圆锥形铅块的体积,由此再根据圆锥的体积公式的变形,h=3V÷s,即可求出铅锥的高.
解:圆锥形铅锥的体积是:
3.14×102×2,
=314×2,
=628(cm3),
铅锥的高是:628×3÷(3.14×52),
=1884÷78.5,
=24(cm),
答:铅锥的高是24cm.
点评:此题主要考查了圆柱与圆锥的体积公式的灵活应用.
5.96厘米
【分析】首先要明确铝块无论被压成什么形状,它的体积是不变的,因此可以分别求出两块铝块的体积,也就等于知道了圆柱形铝块的体积,从而利用圆柱体的体积公式即可求出圆柱形铝块的高。
【详解】(×3.14×202×27+3.14×302×20)÷(3.14×152),
=(3.14×400×9+3.14×900×20)÷(3.14×225),
=(1256×9+2826×20)÷706.5,
=(11304+56520)÷706.5,
=67824÷706.5,
=96(厘米);
答:这个圆的高是96厘米。
6.56.52立方厘米
【详解】试题分析:把一个正方体加工成一个最大的圆锥,关键弄清圆锥的底面直径等于正方体的棱长,圆锥的高也等于正方体的棱长,由此解答.
解:3.14×(6÷2)2×6×,
=3.14×9×6×,
=56.52(立方厘米);
答:削成的圆锥的体积是56.52立方厘米.
点评:此题考查了圆锥的体积计算,以及应用圆锥的体积计算方法解决实际问题.
7.91平方米
【详解】略
8.(1) 50.24m2
(2) 11.2kg
【详解】(1)40 cm=0.4 m
3.14×0.4×5×8=50.24(m2)
答:至少需要50.24 m2装饰板。
(2)50.24÷4.5≈11.2(kg)
答:大约需要11.2 kg油漆。
9.108.56平方厘米
【分析】根据题意可知,物体的表面积=正方体的表面积+圆柱的侧面积,其中圆柱的侧面积=底面周长×高,据此解答。
【详解】
=96+12.56
=108.56(平方厘米)
答:所得物体的表面积是108.56平方厘米。
【点睛】此题考查了组合体表面积的计算,明确挖去一个小圆柱体减少一个圆柱底面的同时又增加了一个圆柱底面,所以只是增加了一个圆柱侧面。
10.659.4平方厘米
【分析】此题先利用侧面积公式:,求出底面半径,根据底面积公式:求出底面积,最后根据圆柱的表面积=侧面积+两个底面积,可求出圆柱的表面积。
【详解】底面半径:31.4÷1÷3.14÷2
=10÷2
=5(厘米)
31.4×16+5×3.14×2
=502.4+157
=659.4(平方厘米)
答:它的表面积是659.4平方厘米。
【点睛】此题主要考查圆柱的表面积的计算方法,根据已知条件,灵活运用侧面积公式以及底面积公式解答。
11.①(1)和(3)
②118.3152升
【分析】①用长方形的长围成一个圆,求出直径,再用长方形的宽,围成一个圆,求出直径,进而求出和那个型号搭配,即可解答;
②再根据圆柱体的体积公式:底面积×高,代入数据,即可解答。
【详解】①12.56÷3.14=4(dm)
9.42÷3.14=3(dm)
直径是4dm,只用图(1)和(3)搭配做成一个无盖水桶。
②3.14×(4÷2)2×9.42
=3.14×22×9.42
=3.14×4×9.42
=12.56×9.42
=118.3152(升)
答:水桶能装水118.3152升。
【点睛】本题考查圆柱体的特征以及圆柱体的体积公式的应用。
12.能;见详解
【分析】根据圆的周长公式,求出圆的直径,用直径与开口的长、厚度与开口的宽比较即可。
【详解】(厘米)
2.5<3
0.2<0.4
答:能放进去。
【点睛】本题主要考查圆柱的特征,注意圆柱的直径与厚度有一项大于开口处就不能放进去。
13.3.2米
【分析】根据圆锥的体积公式:V=πr2h求出这堆小麦的体积,再用这堆小麦的体积除以圆柱的底面积求出粮仓里的小麦高。
【详解】×3.14×(8÷2)2×2.4÷[3.14×(4÷2)2]
=3.14×16×0.8÷[3.14×4]
=3.14×12.8÷12.56
=40.192÷12.56
=3.2(米)
答:粮仓里的小麦高是3.2米。
【点睛】考查了圆柱的体积和圆锥的体积,计算时要认真。
14.150.72立方厘米
【分析】高减少厘米后圆柱的表面积减少37.68平方厘米,先求减少的圆柱的高,用12×=3(厘米),表面积减少的是3厘米的侧面积,用37.68除以3求出底面周长,用底面周长除以圆周率除以3求出底面半径,然后根据圆柱的体积公式:v=sh,把数据代入公式解答。
【详解】减少的圆柱的高:12×=3(厘米),
底面半径是:
37.68÷3÷3.14÷2
=12.56÷3.14÷2
=2(厘米)
原来的体积是:
3.14×22×12
=3.14×4×12
=150.72(立方厘米)
答:原来体积是150.72立方厘米。
【点睛】抓住切割特点,得出减少的表面积是减少的圆柱部分的侧面积,从而求出底面半径是解决本题的关键。
15.164.64立方厘米
【分析】由题目可知,剩下部分的体积=长方体的体积-圆柱的体积;根据长方体的体积公式:长×宽×高;圆柱的体积公式:V=πr2h,把数代入即可求解。
【详解】8×5×6-3.14×2×2×6
=240-75.36
=164.64(立方厘米)
答:剩下部分的体积是164.64立方厘米。
【点睛】本题主要考查长方体以及圆柱的体积公式,熟练掌握它们的体积公式并灵活运用。
16.(1)平方厘米;
(2)平方厘米;
(3)不能
【分析】(1)占桌面的面积也就是圆柱的底面积,根据圆的面积S=πr2,代入数据计算即可。
(2)装饰带的面积=底面周长×宽度;
(3)根据圆柱的体积V=πr2h,求出茶杯的容积与0.5升比较即可。
【详解】(1)
=9×3.14
=28.26(平方厘米)
答:这只茶杯占桌面的大小是28.26平方厘米。
(2)
=3.14×30
=94.2(平方厘米)
答:面积至少有平方厘米。
(3)
=3.14×9×15
=28.26×15
=423.9(立方厘米)
423.9立方厘米=0.4239升
答:不能装满。
【点睛】此题考查了圆柱体的相关应用,明确圆柱的体积和侧面积计算公式,并能灵活运用是解题关键。
17.0.28厘米
【分析】根据圆锥的体积公式:V=πr2h,求出圆锥体铅锤的体积,用圆锥体铅锤的体积除以圆柱形玻璃杯的底面积即可。
【详解】3.14×(8÷2)2×12×÷[3.14×(30÷2)2]
=3.14×16×12×÷[3.14×225]
=50.24×12×÷706.5
=602.88×÷706.5
=200.96÷706.5
≈0.28(厘米)
答:杯里的水大约下降0.28厘米。
【点睛】此题主要考查圆锥体积公式和圆柱体的体积公式的灵活运用,关键是熟记公式。
18.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
【点睛】本题考查学生的空间想象能力,分析底面和背面也需要和正面看到一样多的丝带。
19.平方米
【详解】2×2π÷2×20=40π(平方米)
20.(1) 3.70635m2
(2) 8.895kg
【详解】(1)30 cm=0.3 m 20 cm=0.2 m
40 cm=0.4 m 0.3÷2=0.15(m)
3.14×0.3×3.5+0.2×0.4×4+0.4×0.4-3.14×0.152=3.70635(m2)
答:要漆3.70635 m2。
(2)3.70635×12×0.2≈8.895(kg)
答:一共需要油漆约8.895 kg。
21.45cm,18cm,18cm
【详解】4.5×2×2=18(cm)
答:这个纸盒的长至少是45 cm,宽至少是18 cm,高至少是18 cm。
22.59.2464m3
【分析】实际用土石量=原计划土石量-月亮门体积,月亮门是一个圆柱形,据此可得。
【详解】2÷2=1(m)
24 cm=0.24 m
60-3.14×12×0.24=59.2464(m3)
答:实际用了59.2464 m3土石。
【点睛】注意圆柱的体积计算方法。
23.628立方厘米
【详解】可以用2个相同图形倒扣在一起,形成一个大圆柱体,52×3.14×(6+10)=1256(立方厘米)
1256÷2=628(立方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
