8.1 第1课时 多面体(含答案)--高中数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.1 第1课时 多面体(含答案)--高中数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 495.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 22:44:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章 立体几何初步
8.1 基本立体图形
第1课时 多面体
1.下列实物不能近似看成多面体的是( )
A.钻石 B.骰子 C.足球 D.金字塔
2.下列关于棱柱的命题中,真命题的个数是( )
①同一棱柱的侧棱平行且相等;
②一个棱柱至少有5个面;
③当棱柱的底面是正多边形时,该棱柱一定是正棱柱;
④当棱柱的底面是等腰梯形时,该棱柱一定是平行六面体.
A.1 B.2 C.3 D.4
3.如图所示的几何体中,为棱柱的是 (填写所有正确的序号).
4.下列关于棱锥的叙述,正确的是( )
A.五面体一定是四棱锥 B.五棱锥有六个顶点
C.侧棱都相等的棱锥是正棱锥 D.正棱锥的侧棱都相等
5.如图所示的几何体中,为棱锥的是( )
A.①③ B.①③④ C.①②④ D.③④
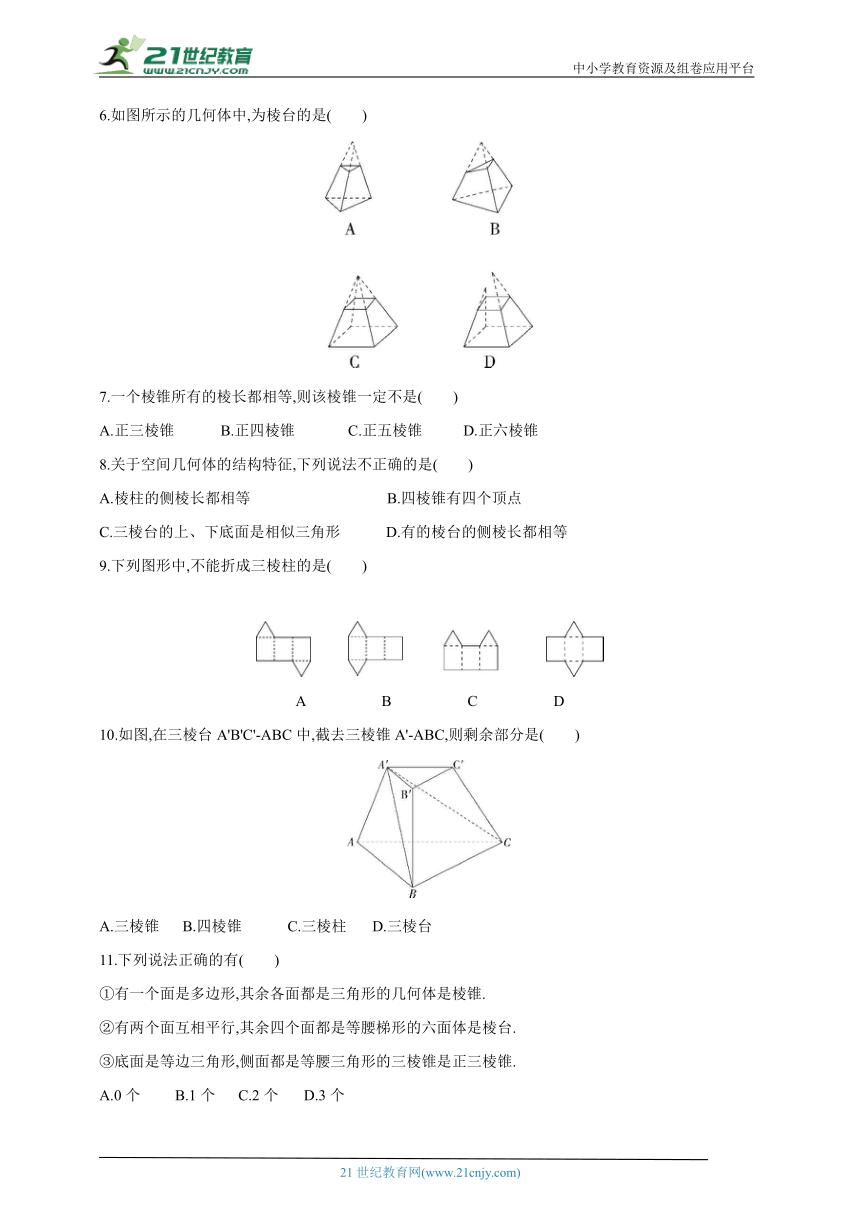
6.如图所示的几何体中,为棱台的是( )
7.一个棱锥所有的棱长都相等,则该棱锥一定不是( )
A.正三棱锥 B.正四棱锥 C.正五棱锥 D.正六棱锥
8.关于空间几何体的结构特征,下列说法不正确的是( )
A.棱柱的侧棱长都相等 B.四棱锥有四个顶点
C.三棱台的上、下底面是相似三角形 D.有的棱台的侧棱长都相等
9.下列图形中,不能折成三棱柱的是( )
A B C D
10.如图,在三棱台A'B'C'-ABC中,截去三棱锥A'-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.三棱台
11.下列说法正确的有( )
①有一个面是多边形,其余各面都是三角形的几何体是棱锥.
②有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
A.0个 B.1个 C.2个 D.3个
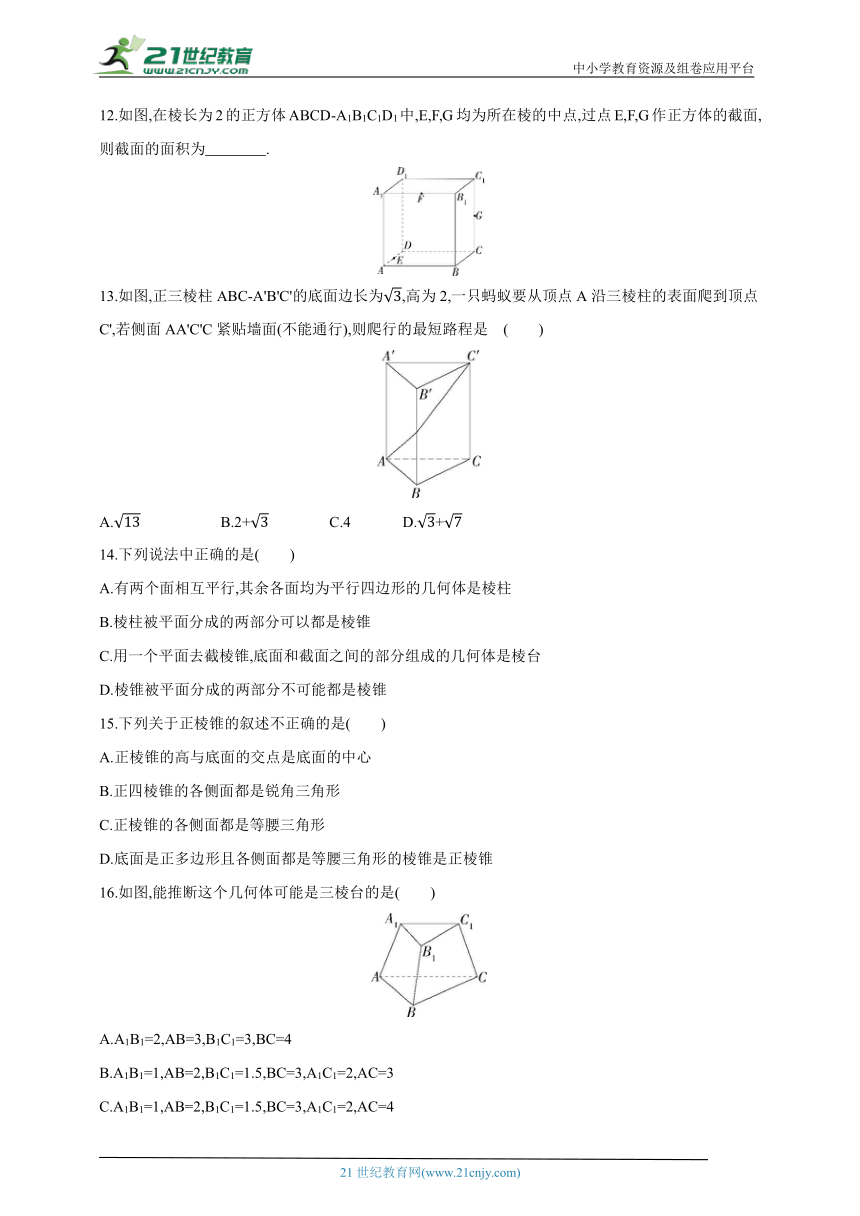
12.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G均为所在棱的中点,过点E,F,G作正方体的截面,则截面的面积为 .
13.如图,正三棱柱ABC-A'B'C'的底面边长为,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C',若侧面AA'C'C紧贴墙面(不能通行),则爬行的最短路程是 ( )
A. B.2+ C.4 D.+
14.下列说法中正确的是( )
A.有两个面相互平行,其余各面均为平行四边形的几何体是棱柱
B.棱柱被平面分成的两部分可以都是棱锥
C.用一个平面去截棱锥,底面和截面之间的部分组成的几何体是棱台
D.棱锥被平面分成的两部分不可能都是棱锥
15.下列关于正棱锥的叙述不正确的是( )
A.正棱锥的高与底面的交点是底面的中心
B.正四棱锥的各侧面都是锐角三角形
C.正棱锥的各侧面都是等腰三角形
D.底面是正多边形且各侧面都是等腰三角形的棱锥是正棱锥
16.如图,能推断这个几何体可能是三棱台的是( )
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=3
C.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=4
D.AB=A1B1,BC=B1C1,CA=C1A1
17.在长方体ABCD-A1B1C1D1中,AB=6,BC=4,AA1=2,P、Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为( )
A.3 B.4 C. D.5
18.(多选)过正方体棱上三点D,E,F(均为棱的中点)的截面过点P(点P为BB1的中点)的是( )
A B C D
19.(多选)在正方体上任意选择4个顶点,它们可能是如下几何图形的4个顶点,这些几何图形可以是( )
A.直角梯形
B.有三个面为等腰直角三角形,一个面为等边三角形的四面体
C.每个面都是等边三角形的四面体
D.每个面都是直角三角形的四面体
20.如图,在将装有水的长方体水槽固定底面一边后倾斜一个小角度,求倾斜后水槽中的水形成的几何体是 .
21.如图,在正三棱锥A-BCD中,∠BAD=30°,侧棱AB=2,BD平行于过点C的截面CB1D1,求截面CB1D1与正三棱锥A-BCD侧面交线构成的三角形的周长的最小值.
22.如图所示的正四棱台的上底面边长为2,下底面边长为8,高为3,求该正四棱台的侧棱长.
北京大兴国际机场的显著特点是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体(所有棱都相等的四面体)在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为2π-3×=π,故其总曲率为4π.求四棱锥的总曲率和三棱柱的总曲率.
参考答案
8.1 基本立体图形
第1课时 多面体
1.答案:C
2.答案:B
3.答案:③⑤
4.答案:D
5.答案:C
6.答案:C
7.答案:D
8.答案:B
9.答案:C
10.答案:B
11.答案:A
12.答案:3
13.答案:A
14.答案:B
15.答案:D
16.答案:C
17.答案:B
18.答案:AD
19.答案:BCD
20.答案:棱柱
21.解析:把正三棱锥A-BCD展开,CC'即是截面与正三棱锥侧面交线构成的三角形周长的最小值.
正三棱锥A-BCD中,∠BAD=30°,∴AC⊥AC',又AB=2,
∴AC=AC'=AB=2,∴CC'=2,
∴周长的最小值是2.
22.解析:连接O'A',OA,过A'作A'E⊥OA,交OA于点E,
∵正四棱台的上底面边长为2,下底面边长为8,高为3,
∴A'O'=OE=A'C'=,AO=AC=4,A'E=O'O=3,
∴AE=AO-OE=3,
∴AA'==6.
故该正四棱台的侧棱长为6.
23.解析:四棱锥是一种五面体,它的总曲率等于五面体5个顶点的曲率之和.
如图,四棱锥P-ABCD的表面由4个三角形,1个四边形组成,面角和为4×π+1×2π=6π,
则其总曲率为2π×5-6π=4π.
三棱柱也是五面体,它的总曲率等于五面体6个顶点的曲率之和.
如图,面角和为2×π+3×2π=8π,
则其总曲率为2π×6-8π=4π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 立体几何初步
8.1 基本立体图形
第1课时 多面体
1.下列实物不能近似看成多面体的是( )
A.钻石 B.骰子 C.足球 D.金字塔
2.下列关于棱柱的命题中,真命题的个数是( )
①同一棱柱的侧棱平行且相等;
②一个棱柱至少有5个面;
③当棱柱的底面是正多边形时,该棱柱一定是正棱柱;
④当棱柱的底面是等腰梯形时,该棱柱一定是平行六面体.
A.1 B.2 C.3 D.4
3.如图所示的几何体中,为棱柱的是 (填写所有正确的序号).
4.下列关于棱锥的叙述,正确的是( )
A.五面体一定是四棱锥 B.五棱锥有六个顶点
C.侧棱都相等的棱锥是正棱锥 D.正棱锥的侧棱都相等
5.如图所示的几何体中,为棱锥的是( )
A.①③ B.①③④ C.①②④ D.③④
6.如图所示的几何体中,为棱台的是( )
7.一个棱锥所有的棱长都相等,则该棱锥一定不是( )
A.正三棱锥 B.正四棱锥 C.正五棱锥 D.正六棱锥
8.关于空间几何体的结构特征,下列说法不正确的是( )
A.棱柱的侧棱长都相等 B.四棱锥有四个顶点
C.三棱台的上、下底面是相似三角形 D.有的棱台的侧棱长都相等
9.下列图形中,不能折成三棱柱的是( )
A B C D
10.如图,在三棱台A'B'C'-ABC中,截去三棱锥A'-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.三棱台
11.下列说法正确的有( )
①有一个面是多边形,其余各面都是三角形的几何体是棱锥.
②有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.
③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
A.0个 B.1个 C.2个 D.3个
12.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G均为所在棱的中点,过点E,F,G作正方体的截面,则截面的面积为 .
13.如图,正三棱柱ABC-A'B'C'的底面边长为,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C',若侧面AA'C'C紧贴墙面(不能通行),则爬行的最短路程是 ( )
A. B.2+ C.4 D.+
14.下列说法中正确的是( )
A.有两个面相互平行,其余各面均为平行四边形的几何体是棱柱
B.棱柱被平面分成的两部分可以都是棱锥
C.用一个平面去截棱锥,底面和截面之间的部分组成的几何体是棱台
D.棱锥被平面分成的两部分不可能都是棱锥
15.下列关于正棱锥的叙述不正确的是( )
A.正棱锥的高与底面的交点是底面的中心
B.正四棱锥的各侧面都是锐角三角形
C.正棱锥的各侧面都是等腰三角形
D.底面是正多边形且各侧面都是等腰三角形的棱锥是正棱锥
16.如图,能推断这个几何体可能是三棱台的是( )
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=3
C.A1B1=1,AB=2,B1C1=1.5,BC=3,A1C1=2,AC=4
D.AB=A1B1,BC=B1C1,CA=C1A1
17.在长方体ABCD-A1B1C1D1中,AB=6,BC=4,AA1=2,P、Q分别为棱AA1,C1D1的中点,则从点P出发,沿长方体表面到达点Q的最短路径的长度为( )
A.3 B.4 C. D.5
18.(多选)过正方体棱上三点D,E,F(均为棱的中点)的截面过点P(点P为BB1的中点)的是( )
A B C D
19.(多选)在正方体上任意选择4个顶点,它们可能是如下几何图形的4个顶点,这些几何图形可以是( )
A.直角梯形
B.有三个面为等腰直角三角形,一个面为等边三角形的四面体
C.每个面都是等边三角形的四面体
D.每个面都是直角三角形的四面体
20.如图,在将装有水的长方体水槽固定底面一边后倾斜一个小角度,求倾斜后水槽中的水形成的几何体是 .
21.如图,在正三棱锥A-BCD中,∠BAD=30°,侧棱AB=2,BD平行于过点C的截面CB1D1,求截面CB1D1与正三棱锥A-BCD侧面交线构成的三角形的周长的最小值.
22.如图所示的正四棱台的上底面边长为2,下底面边长为8,高为3,求该正四棱台的侧棱长.
北京大兴国际机场的显著特点是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体(所有棱都相等的四面体)在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为2π-3×=π,故其总曲率为4π.求四棱锥的总曲率和三棱柱的总曲率.
参考答案
8.1 基本立体图形
第1课时 多面体
1.答案:C
2.答案:B
3.答案:③⑤
4.答案:D
5.答案:C
6.答案:C
7.答案:D
8.答案:B
9.答案:C
10.答案:B
11.答案:A
12.答案:3
13.答案:A
14.答案:B
15.答案:D
16.答案:C
17.答案:B
18.答案:AD
19.答案:BCD
20.答案:棱柱
21.解析:把正三棱锥A-BCD展开,CC'即是截面与正三棱锥侧面交线构成的三角形周长的最小值.
正三棱锥A-BCD中,∠BAD=30°,∴AC⊥AC',又AB=2,
∴AC=AC'=AB=2,∴CC'=2,
∴周长的最小值是2.
22.解析:连接O'A',OA,过A'作A'E⊥OA,交OA于点E,
∵正四棱台的上底面边长为2,下底面边长为8,高为3,
∴A'O'=OE=A'C'=,AO=AC=4,A'E=O'O=3,
∴AE=AO-OE=3,
∴AA'==6.
故该正四棱台的侧棱长为6.
23.解析:四棱锥是一种五面体,它的总曲率等于五面体5个顶点的曲率之和.
如图,四棱锥P-ABCD的表面由4个三角形,1个四边形组成,面角和为4×π+1×2π=6π,
则其总曲率为2π×5-6π=4π.
三棱柱也是五面体,它的总曲率等于五面体6个顶点的曲率之和.
如图,面角和为2×π+3×2π=8π,
则其总曲率为2π×6-8π=4π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
