8.1 第2课时 旋转体(含答案)--高中数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.1 第2课时 旋转体(含答案)--高中数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 22:45:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第八章 立体几何初步
8.1 基本立体图形
第2课时 旋转体
1.下列关于圆柱的说法中,不正确的是( )
A.分别以矩形(非正方形)的长和宽所在的直线为旋转轴旋转一周而得到的两个圆柱是两个不同的圆柱
B.用平行于圆柱底面的平面截圆柱,截面是与底面全等的圆面
C.用一个不平行于圆柱底面的平面截圆柱,截面是一个圆面
D.以一个矩形一组对边中点的连线所在的直线为旋转轴,各边旋转180°而形成的曲面所围成的几何体是圆柱
2.一个圆锥的高为2 cm,母线与旋转轴的夹角为30°,求圆锥的母线长及圆锥的轴截面的面积.
3.如图,某工厂生产的一种机器零件原胚是一个中空的圆台,中空部分呈圆柱形状,且圆柱底面圆心与圆台底面圆心重合,该零件原胚可由下面图形中的一个绕对称轴(直线l)旋转而成,这个图形是( )
A B C D
4.下列说法正确的是( )
A.到定点的距离等于定长的点的集合是球
B.球面上不同的三点可能在同一直线上
C.球面上任意两点的连线是球的直径
D.球心与截面圆心(截面不过球心)的连线垂直于该截面
5.请描述下列组合体是由哪些几何体组成的.
6.下列命题中正确命题的个数是 ( )
①圆柱的轴截面是过母线的截面中面积最大的一个;
②用任意一个平面去截球得到的截面图形一定是一个圆;
③用任意一个平面去截圆锥得到的截面图形一定是一个圆.
A.0 B.1 C.2 D.3
7.将一个等腰梯形绕着它较长的底边所在的直线旋转一周,所得到的几何体可拆分为( )
A.一个圆台、两个圆锥 B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
8.如图,阴影部分绕虚线旋转一周形成的几何体为( )
A.一个球体 B.一个球体中间挖去一个圆柱
C.一个圆柱 D.一个球体中间挖去一个长方体
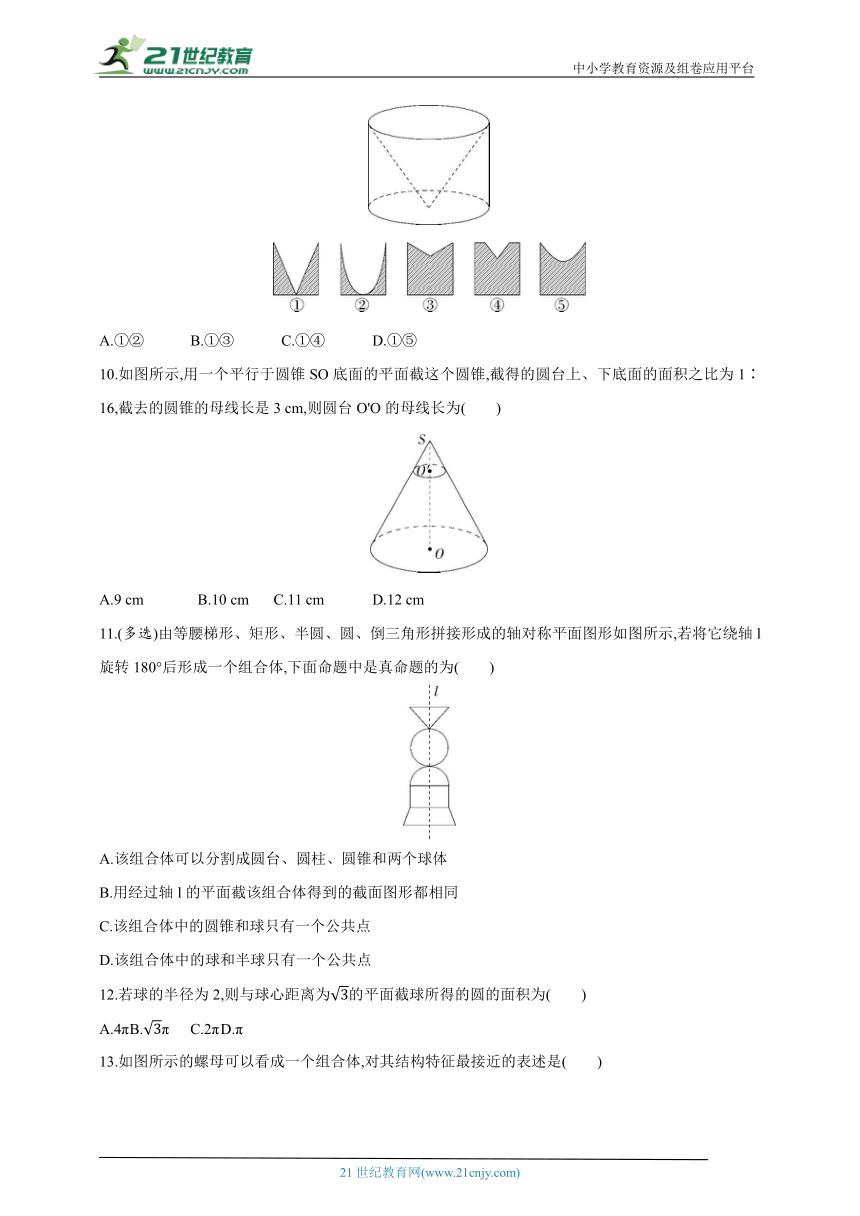
9.如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面、下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①② B.①③ C.①④ D.①⑤
10.如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得的圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,则圆台O'O的母线长为( )
A.9 cm B.10 cm C.11 cm D.12 cm
11.(多选)由等腰梯形、矩形、半圆、圆、倒三角形拼接形成的轴对称平面图形如图所示,若将它绕轴l旋转180°后形成一个组合体,下面命题中是真命题的为( )
A.该组合体可以分割成圆台、圆柱、圆锥和两个球体
B.用经过轴l的平面截该组合体得到的截面图形都相同
C.该组合体中的圆锥和球只有一个公共点
D.该组合体中的球和半球只有一个公共点
12.若球的半径为2,则与球心距离为的平面截球所得的圆的面积为( )
A.4π B.π C.2π D.π
13.如图所示的螺母可以看成一个组合体,对其结构特征最接近的表述是( )
A.一个六棱柱中挖去一个棱柱
B.一个六棱柱中挖去一个棱锥
C.一个六棱柱中挖去一个圆柱
D.一个六棱柱中挖去一个圆台
14.给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;
④棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
15.碾子是我国古代人民发明的一种把米、麦、豆等粮食加工成粉末的器具,如图,近似圆柱形的碾子的轴固定在经过圆盘圆心且垂直于圆盘的木桩上,当人推动木柄时,碾子在圆盘上滚动.若人推动木柄绕圆盘转动1周,碾子恰好滚动了3圈,则该圆柱形碾子的高与其底面圆的直径之比为( )
A.3∶1 B.3∶2 C.1∶3 D.2∶3
16.一个球体被两个平行平面所截,夹在两平行平面间的部分叫做“球台”,两平行平面间的距离叫做球台的高.如图1,西晋越窑的某个“卧足杯”的外形可近似看成如图2所示的球台,已知杯底的直径为2cm,杯口直径为4cm,杯的深度为cm,则该卧足杯侧面所在球面的半径为 ( )
A.5 cm B.2 cm C. cm D. cm
17.已知圆锥SO的底面半径R=5,高H=12.
(1)求圆锥SO的母线长.
(2)设圆锥SO的内接圆柱OO'的高为h,当h为何值时,内接圆柱OO'的轴截面面积最大 求出最大值.
参考答案
8.1 基本立体图形
第2课时 旋转体
1.答案:C
2.解析:轴截面SAB如图所示:
圆锥SO的底面直径为AB,高为SO,母线为SA,则∠ASO=30°.
在Rt△SOA中,AO=SO·tan 30°=(cm),
SA==(cm),
所以S△ASB=SO·2AO=(cm2).
所以圆锥的母线长为 cm,
圆锥的轴截面的面积为 cm2.
3.答案:B
4.答案:D
5.解析:①是由一个圆锥和一个圆台拼接而成的组合体;
②是由一个长方体截去一个三棱锥得到的组合体;
③是由一个圆柱挖去一个三棱锥得到的组合体.
6.答案:C
7.答案:D
8.答案:B
9.答案:D
10.答案:A
11.答案:BCD
12.答案:D
13.答案:C
14.答案:A
15.答案:B
16.答案:A
17.解析:(1)∵圆锥SO的底面半径R=5,高H=12,
∴圆锥SO的母线长l==13.
(2)作出圆锥、圆柱的轴截面如图所示,
其中SO=12,OA=OB=5,OO'=h(0设圆柱底面半径为r,则=,即r=.
设圆柱的轴截面面积为S',则S'=2r·h=(12h-h2)=[-(h-6)2+36](0∴当h=6时,S'有最大值,最大值为30.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 立体几何初步
8.1 基本立体图形
第2课时 旋转体
1.下列关于圆柱的说法中,不正确的是( )
A.分别以矩形(非正方形)的长和宽所在的直线为旋转轴旋转一周而得到的两个圆柱是两个不同的圆柱
B.用平行于圆柱底面的平面截圆柱,截面是与底面全等的圆面
C.用一个不平行于圆柱底面的平面截圆柱,截面是一个圆面
D.以一个矩形一组对边中点的连线所在的直线为旋转轴,各边旋转180°而形成的曲面所围成的几何体是圆柱
2.一个圆锥的高为2 cm,母线与旋转轴的夹角为30°,求圆锥的母线长及圆锥的轴截面的面积.
3.如图,某工厂生产的一种机器零件原胚是一个中空的圆台,中空部分呈圆柱形状,且圆柱底面圆心与圆台底面圆心重合,该零件原胚可由下面图形中的一个绕对称轴(直线l)旋转而成,这个图形是( )
A B C D
4.下列说法正确的是( )
A.到定点的距离等于定长的点的集合是球
B.球面上不同的三点可能在同一直线上
C.球面上任意两点的连线是球的直径
D.球心与截面圆心(截面不过球心)的连线垂直于该截面
5.请描述下列组合体是由哪些几何体组成的.
6.下列命题中正确命题的个数是 ( )
①圆柱的轴截面是过母线的截面中面积最大的一个;
②用任意一个平面去截球得到的截面图形一定是一个圆;
③用任意一个平面去截圆锥得到的截面图形一定是一个圆.
A.0 B.1 C.2 D.3
7.将一个等腰梯形绕着它较长的底边所在的直线旋转一周,所得到的几何体可拆分为( )
A.一个圆台、两个圆锥 B.两个圆柱、一个圆锥
C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥
8.如图,阴影部分绕虚线旋转一周形成的几何体为( )
A.一个球体 B.一个球体中间挖去一个圆柱
C.一个圆柱 D.一个球体中间挖去一个长方体
9.如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面、下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是( )
A.①② B.①③ C.①④ D.①⑤
10.如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得的圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3 cm,则圆台O'O的母线长为( )
A.9 cm B.10 cm C.11 cm D.12 cm
11.(多选)由等腰梯形、矩形、半圆、圆、倒三角形拼接形成的轴对称平面图形如图所示,若将它绕轴l旋转180°后形成一个组合体,下面命题中是真命题的为( )
A.该组合体可以分割成圆台、圆柱、圆锥和两个球体
B.用经过轴l的平面截该组合体得到的截面图形都相同
C.该组合体中的圆锥和球只有一个公共点
D.该组合体中的球和半球只有一个公共点
12.若球的半径为2,则与球心距离为的平面截球所得的圆的面积为( )
A.4π B.π C.2π D.π
13.如图所示的螺母可以看成一个组合体,对其结构特征最接近的表述是( )
A.一个六棱柱中挖去一个棱柱
B.一个六棱柱中挖去一个棱锥
C.一个六棱柱中挖去一个圆柱
D.一个六棱柱中挖去一个圆台
14.给出下列命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥;
④棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确命题的个数是( )
A.0 B.1 C.2 D.3
15.碾子是我国古代人民发明的一种把米、麦、豆等粮食加工成粉末的器具,如图,近似圆柱形的碾子的轴固定在经过圆盘圆心且垂直于圆盘的木桩上,当人推动木柄时,碾子在圆盘上滚动.若人推动木柄绕圆盘转动1周,碾子恰好滚动了3圈,则该圆柱形碾子的高与其底面圆的直径之比为( )
A.3∶1 B.3∶2 C.1∶3 D.2∶3
16.一个球体被两个平行平面所截,夹在两平行平面间的部分叫做“球台”,两平行平面间的距离叫做球台的高.如图1,西晋越窑的某个“卧足杯”的外形可近似看成如图2所示的球台,已知杯底的直径为2cm,杯口直径为4cm,杯的深度为cm,则该卧足杯侧面所在球面的半径为 ( )
A.5 cm B.2 cm C. cm D. cm
17.已知圆锥SO的底面半径R=5,高H=12.
(1)求圆锥SO的母线长.
(2)设圆锥SO的内接圆柱OO'的高为h,当h为何值时,内接圆柱OO'的轴截面面积最大 求出最大值.
参考答案
8.1 基本立体图形
第2课时 旋转体
1.答案:C
2.解析:轴截面SAB如图所示:
圆锥SO的底面直径为AB,高为SO,母线为SA,则∠ASO=30°.
在Rt△SOA中,AO=SO·tan 30°=(cm),
SA==(cm),
所以S△ASB=SO·2AO=(cm2).
所以圆锥的母线长为 cm,
圆锥的轴截面的面积为 cm2.
3.答案:B
4.答案:D
5.解析:①是由一个圆锥和一个圆台拼接而成的组合体;
②是由一个长方体截去一个三棱锥得到的组合体;
③是由一个圆柱挖去一个三棱锥得到的组合体.
6.答案:C
7.答案:D
8.答案:B
9.答案:D
10.答案:A
11.答案:BCD
12.答案:D
13.答案:C
14.答案:A
15.答案:B
16.答案:A
17.解析:(1)∵圆锥SO的底面半径R=5,高H=12,
∴圆锥SO的母线长l==13.
(2)作出圆锥、圆柱的轴截面如图所示,
其中SO=12,OA=OB=5,OO'=h(0
设圆柱的轴截面面积为S',则S'=2r·h=(12h-h2)=[-(h-6)2+36](0
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
