8.3.1 棱柱、棱锥、棱台的表面积和体积(含答案)--高中数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.3.1 棱柱、棱锥、棱台的表面积和体积(含答案)--高中数学人教A版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 616.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第八章 立体几何初步
8.3 简单几何体的表面积与体积
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.已知正三棱柱的体积为,且底面边长与高相等,则该正三棱柱侧面的对角线长为( )
A.1 B. C.2 D.
2.如图,等边三角形△ABC的边长为4,D,E,F分别为AB,BC和AC的中点,将△BDE、△CEF、△ADF分别沿DE、EF和DF折起,使A,B,C三点重合,求折叠后得到的四面体的体积.
3.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A.56 B.28 C. D.
4.南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为(≈2.65)( )
A.1.0×109 m3 B.1.2×109 m3 C.1.4×109 m3 D.1.6×109 m3
5.《九章算术》中将正四棱台(棱台的上下底面均为正方形)称为方亭.如图,现有一方亭ABCD-EFHG,其中上底面与下底面的面积之比为1∶4,方亭的高h=EF,BF=EF,方亭的四个侧面均为全等的等腰梯形,已知方亭四个侧面的面积之和为12,则方亭的体积为( )
A.24 B. C. D.16
6.已知长方体的表面积是24 cm2,过同一顶点的三条棱长之和是6 cm,则它的体对角线长是 ( )
A. cm B.4 cm C.3 cm D.2 cm
7.直三棱柱ABC-A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=,D是线段A1B1的中点.棱柱ABC-A1B1C1被平面AC1D分成的两部分的体积比为 ( )
A.1∶3 B.1∶4 C.2∶3 D.1∶5
8.如图1所示,已知正方体面对角线长为a,沿阴影面将它切割成两部分,拼成如图2所示的几何体,那么此几何体的表面积为( )
图1 图2
A.(1+2)a2 B.(2+)a2 C.(3+2)a2 D.(4+2)a2
9.2022年北京冬奥会的成功举办使北京成为奥运史上第一座“双奥之城”.其中2008年北京奥运会的标志性场馆之一的“水立方”摇身一变成为了“冰立方”.“水立方”的设计灵感来自威尔—弗兰泡沫,威尔—弗兰泡沫是对开尔文胞体的改进,开尔文胞体是一种多面体,它由正六边形和正方形围成(其中每一个顶点处有一个正方形和两个正六边形),已知该多面体共有24个顶点,且棱长为2,则该多面体的表面积是( )
A.24(+1) B.24+6 C.48+24 D.16+8
10.如图,用钢浇铸一个厚度均匀,且表面积为2平方米的正四棱锥形有盖容器,设容器的高为h米,盖子的边长为a米.
(1)求a关于h的函数解析式.
(2)当h为何值时,容器的容积V最大 并求出V的最大值.
如图,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,
EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
12.一个相对棱长都相等的四面体,其三组对棱长分别为,,,求此四面体的体积.
13.已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为 .
14.中国古代数学著作《九章算术注》中记载:“斜解立方(即长方体)得二堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.如图所示,自左向右依次为立方、堑堵、阳马、鳖臑,若AB=BC=1,AA1=2,则鳖臑的表面积为( )
A.2+ B.2+ C.1+ D.1+
15.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形边长的比值为( )
A. B. C. D.
16.在直三棱柱ABC-A1B1C1中,AB=AC=BC=2,AA1=1,则点A到平面A1BC的距离为( )
A. B. C. D.
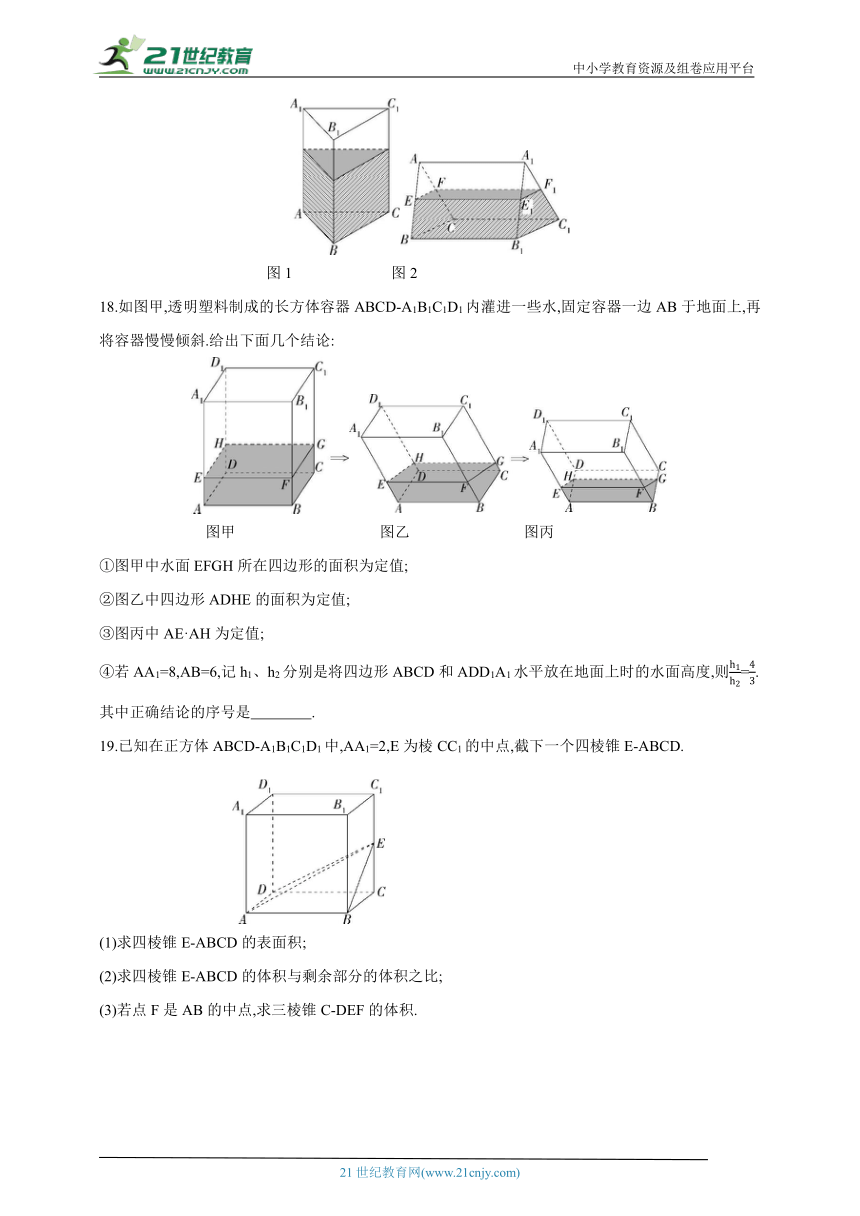
17.有一个封闭的正三棱柱容器,高为12,内装水若干(如图1,底面处于水平状态),将容器放倒(如图2,一个侧面处于水平状态),这时水面与各棱的交点E、F、E1、F1分别为所在棱的中点,则图1中水面的高度为 .
图1 图2
18.如图甲,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器一边AB于地面上,再将容器慢慢倾斜.给出下面几个结论:
图甲 图乙 图丙
①图甲中水面EFGH所在四边形的面积为定值;
②图乙中四边形ADHE的面积为定值;
③图丙中AE·AH为定值;
④若AA1=8,AB=6,记h1、h2分别是将四边形ABCD和ADD1A1水平放在地面上时的水面高度,则=.
其中正确结论的序号是 .
19.已知在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点,截下一个四棱锥E-ABCD.
(1)求四棱锥E-ABCD的表面积;
(2)求四棱锥E-ABCD的体积与剩余部分的体积之比;
(3)若点F是AB的中点,求三棱锥C-DEF的体积.
20.如图,两个相同的正四棱锥底面重合组成一个八面体,可放入一个底面为正方形的长方体内,且长方体的正方形底面边长为2,高为4,已知两个正四棱锥重合的底面与长方体的正方形底面平行,八面体的各顶点均在长方体的表面上.
(1)若点A,B,C,D恰为长方体各侧面对角线的交点,求该八面体的体积;
(2)求该八面体表面积S的取值范围.
参考答案
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.答案:C
2.解析:如图所示.
设A,B,C三点重合于S,折叠后得到的四面体为正四面体S-DEF,
设O为S在底面的投影,则正四面体的棱长为2,且SO⊥OD.
OD=××2=,则SO==,
所以折叠后得到的四面体的体积V=××2×2××=.
3.答案:D
4.答案:C
5.答案:C
6.答案:D
7.答案:D
8.答案:D
9.答案:C
10.解析:(1)连接AC,BD,交点为O,连接PO,则PO即为正四棱锥的高,取CD的中点E,
连接OE,EP,则OE=a,
由勾股定理得,PE=,
由题意得,a2+4×a=2,
整理得,a=.
(2)V=a2h==,
因为h+≥2=2,当且仅当h=,即h=1时,等号成立,故V≤,
故当h=1时,容器的容积V最大,Vmax=.
解析:如图,连接EB,EC,AC,
则V四棱锥E-ABCD=×42×3=16.
因为AB=2EF,EF∥AB,所以S△EAB=2S△BEF.
所以V三棱锥F-EBC=V三棱锥C-EFB=V三棱锥C-ABE=V三棱锥E-ABC =×V四棱锥E-ABCD=4
(将三棱锥F-EBC的体积进行多次转化,最终转化为四棱锥E-ABCD体积的四分之一).
所以该多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=20.
解析:如图,将四面体补全为长方体,
设长方体ABCD-A1B1C1D1中,AA1=x,AD=y,AB=z,
不妨设BD=,A1D=,A1B=,
则有解得
是,=----=xyz-×xyz-×xyz-×xyz-×xyz=xyz=2.
13.答案:
14.答案:A
15.答案:C
16.答案:B
17.答案:9
18.答案:②③④
19.解析:(1)易知△ABE≌△ADE,△BCE≌△DCE,所以S△ABE=S△ADE,S△BCE=S△DCE.
S正方形ABCD=22=4,S△BCE=BC·CE=×2×1=1,
BE==,则S△ABE=AB·BE=×2×=,
所以四棱锥E-ABCD的表面积S=S正方形ABCD+S△BCE+S△DCE+S△ABE+S△ADE=4+2×1+2×=6+2.
(2)因为EC为四棱锥E-ABCD的高,且EC=1,
所以V四棱锥E-ABCD=S正方形ABCD·EC=×4×1=.
又正方体体积V1=23=8,
所以V四棱锥E-ABCD∶V1=∶8=1∶6.
设剩余部分的体积为V2,
则V四棱锥E-ABCD∶V2=1∶5.
(3)S△CDF=S正方形ABCD=2,
易知EC为三棱锥E-CDF的高,故V三棱锥C-DEF=V三棱锥E-CDF=S△CDF·EC=×2×1=.
20.解析:(1)∵点A,B,C,D恰为长方体各侧面对角线的交点,
∴AB=BC=CD=AD=, ∴V八面体=2V四棱锥E-ABCD=2××××2=.
(2)如图1,设平面ABCD截长方体所得截面为A'B'C'D',且A'B'C'D'的中心为O,过点O作OG⊥A'B',垂足为G,连接OA.
图1 图2
由对称性,不妨设AA'=x(0≤x≤1),
则AG=1-x,AO2=AG2+GO2=(1-x)2+1,
AD2=(2-x)2+x2=2(x2-2x)+4.
设AD的中点为H,连接HE,如图2,
AE2=DE2=AO2+OE2=(1-x)2+1+22=x2-2x+6,
AH2==(x2-2x)+1,
EH2=AE2-AH2=(x2-2x)+5,
所以=AD2·EH2=[2(x2-2x)+4]·=+3(x2-2x)+5.
因为0≤x≤1,所以-1≤x2-2x≤0,
则≤+3(x2-2x)+5≤5,
故≤S△ADE≤,即12≤8S△ADE≤8,
所以12≤S≤8,
所以此八面体的表面积S的取值范围为[12,8].
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章 立体几何初步
8.3 简单几何体的表面积与体积
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.已知正三棱柱的体积为,且底面边长与高相等,则该正三棱柱侧面的对角线长为( )
A.1 B. C.2 D.
2.如图,等边三角形△ABC的边长为4,D,E,F分别为AB,BC和AC的中点,将△BDE、△CEF、△ADF分别沿DE、EF和DF折起,使A,B,C三点重合,求折叠后得到的四面体的体积.
3.正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A.56 B.28 C. D.
4.南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2;水位为海拔157.5 m时,相应水面的面积为180.0 km2.将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为(≈2.65)( )
A.1.0×109 m3 B.1.2×109 m3 C.1.4×109 m3 D.1.6×109 m3
5.《九章算术》中将正四棱台(棱台的上下底面均为正方形)称为方亭.如图,现有一方亭ABCD-EFHG,其中上底面与下底面的面积之比为1∶4,方亭的高h=EF,BF=EF,方亭的四个侧面均为全等的等腰梯形,已知方亭四个侧面的面积之和为12,则方亭的体积为( )
A.24 B. C. D.16
6.已知长方体的表面积是24 cm2,过同一顶点的三条棱长之和是6 cm,则它的体对角线长是 ( )
A. cm B.4 cm C.3 cm D.2 cm
7.直三棱柱ABC-A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=,D是线段A1B1的中点.棱柱ABC-A1B1C1被平面AC1D分成的两部分的体积比为 ( )
A.1∶3 B.1∶4 C.2∶3 D.1∶5
8.如图1所示,已知正方体面对角线长为a,沿阴影面将它切割成两部分,拼成如图2所示的几何体,那么此几何体的表面积为( )
图1 图2
A.(1+2)a2 B.(2+)a2 C.(3+2)a2 D.(4+2)a2
9.2022年北京冬奥会的成功举办使北京成为奥运史上第一座“双奥之城”.其中2008年北京奥运会的标志性场馆之一的“水立方”摇身一变成为了“冰立方”.“水立方”的设计灵感来自威尔—弗兰泡沫,威尔—弗兰泡沫是对开尔文胞体的改进,开尔文胞体是一种多面体,它由正六边形和正方形围成(其中每一个顶点处有一个正方形和两个正六边形),已知该多面体共有24个顶点,且棱长为2,则该多面体的表面积是( )
A.24(+1) B.24+6 C.48+24 D.16+8
10.如图,用钢浇铸一个厚度均匀,且表面积为2平方米的正四棱锥形有盖容器,设容器的高为h米,盖子的边长为a米.
(1)求a关于h的函数解析式.
(2)当h为何值时,容器的容积V最大 并求出V的最大值.
如图,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,
EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
12.一个相对棱长都相等的四面体,其三组对棱长分别为,,,求此四面体的体积.
13.已知正方体ABCD-A1B1C1D1的棱长为2,M、N分别为BB1、AB的中点,则三棱锥A-NMD1的体积为 .
14.中国古代数学著作《九章算术注》中记载:“斜解立方(即长方体)得二堑堵,斜解堑堵,其一为阳马,其一为鳖臑”.如图所示,自左向右依次为立方、堑堵、阳马、鳖臑,若AB=BC=1,AA1=2,则鳖臑的表面积为( )
A.2+ B.2+ C.1+ D.1+
15.埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形边长的比值为( )
A. B. C. D.
16.在直三棱柱ABC-A1B1C1中,AB=AC=BC=2,AA1=1,则点A到平面A1BC的距离为( )
A. B. C. D.
17.有一个封闭的正三棱柱容器,高为12,内装水若干(如图1,底面处于水平状态),将容器放倒(如图2,一个侧面处于水平状态),这时水面与各棱的交点E、F、E1、F1分别为所在棱的中点,则图1中水面的高度为 .
图1 图2
18.如图甲,透明塑料制成的长方体容器ABCD-A1B1C1D1内灌进一些水,固定容器一边AB于地面上,再将容器慢慢倾斜.给出下面几个结论:
图甲 图乙 图丙
①图甲中水面EFGH所在四边形的面积为定值;
②图乙中四边形ADHE的面积为定值;
③图丙中AE·AH为定值;
④若AA1=8,AB=6,记h1、h2分别是将四边形ABCD和ADD1A1水平放在地面上时的水面高度,则=.
其中正确结论的序号是 .
19.已知在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点,截下一个四棱锥E-ABCD.
(1)求四棱锥E-ABCD的表面积;
(2)求四棱锥E-ABCD的体积与剩余部分的体积之比;
(3)若点F是AB的中点,求三棱锥C-DEF的体积.
20.如图,两个相同的正四棱锥底面重合组成一个八面体,可放入一个底面为正方形的长方体内,且长方体的正方形底面边长为2,高为4,已知两个正四棱锥重合的底面与长方体的正方形底面平行,八面体的各顶点均在长方体的表面上.
(1)若点A,B,C,D恰为长方体各侧面对角线的交点,求该八面体的体积;
(2)求该八面体表面积S的取值范围.
参考答案
8.3.1 棱柱、棱锥、棱台的表面积和体积
1.答案:C
2.解析:如图所示.
设A,B,C三点重合于S,折叠后得到的四面体为正四面体S-DEF,
设O为S在底面的投影,则正四面体的棱长为2,且SO⊥OD.
OD=××2=,则SO==,
所以折叠后得到的四面体的体积V=××2×2××=.
3.答案:D
4.答案:C
5.答案:C
6.答案:D
7.答案:D
8.答案:D
9.答案:C
10.解析:(1)连接AC,BD,交点为O,连接PO,则PO即为正四棱锥的高,取CD的中点E,
连接OE,EP,则OE=a,
由勾股定理得,PE=,
由题意得,a2+4×a=2,
整理得,a=.
(2)V=a2h==,
因为h+≥2=2,当且仅当h=,即h=1时,等号成立,故V≤,
故当h=1时,容器的容积V最大,Vmax=.
解析:如图,连接EB,EC,AC,
则V四棱锥E-ABCD=×42×3=16.
因为AB=2EF,EF∥AB,所以S△EAB=2S△BEF.
所以V三棱锥F-EBC=V三棱锥C-EFB=V三棱锥C-ABE=V三棱锥E-ABC =×V四棱锥E-ABCD=4
(将三棱锥F-EBC的体积进行多次转化,最终转化为四棱锥E-ABCD体积的四分之一).
所以该多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=20.
解析:如图,将四面体补全为长方体,
设长方体ABCD-A1B1C1D1中,AA1=x,AD=y,AB=z,
不妨设BD=,A1D=,A1B=,
则有解得
是,=----=xyz-×xyz-×xyz-×xyz-×xyz=xyz=2.
13.答案:
14.答案:A
15.答案:C
16.答案:B
17.答案:9
18.答案:②③④
19.解析:(1)易知△ABE≌△ADE,△BCE≌△DCE,所以S△ABE=S△ADE,S△BCE=S△DCE.
S正方形ABCD=22=4,S△BCE=BC·CE=×2×1=1,
BE==,则S△ABE=AB·BE=×2×=,
所以四棱锥E-ABCD的表面积S=S正方形ABCD+S△BCE+S△DCE+S△ABE+S△ADE=4+2×1+2×=6+2.
(2)因为EC为四棱锥E-ABCD的高,且EC=1,
所以V四棱锥E-ABCD=S正方形ABCD·EC=×4×1=.
又正方体体积V1=23=8,
所以V四棱锥E-ABCD∶V1=∶8=1∶6.
设剩余部分的体积为V2,
则V四棱锥E-ABCD∶V2=1∶5.
(3)S△CDF=S正方形ABCD=2,
易知EC为三棱锥E-CDF的高,故V三棱锥C-DEF=V三棱锥E-CDF=S△CDF·EC=×2×1=.
20.解析:(1)∵点A,B,C,D恰为长方体各侧面对角线的交点,
∴AB=BC=CD=AD=, ∴V八面体=2V四棱锥E-ABCD=2××××2=.
(2)如图1,设平面ABCD截长方体所得截面为A'B'C'D',且A'B'C'D'的中心为O,过点O作OG⊥A'B',垂足为G,连接OA.
图1 图2
由对称性,不妨设AA'=x(0≤x≤1),
则AG=1-x,AO2=AG2+GO2=(1-x)2+1,
AD2=(2-x)2+x2=2(x2-2x)+4.
设AD的中点为H,连接HE,如图2,
AE2=DE2=AO2+OE2=(1-x)2+1+22=x2-2x+6,
AH2==(x2-2x)+1,
EH2=AE2-AH2=(x2-2x)+5,
所以=AD2·EH2=[2(x2-2x)+4]·=+3(x2-2x)+5.
因为0≤x≤1,所以-1≤x2-2x≤0,
则≤+3(x2-2x)+5≤5,
故≤S△ADE≤,即12≤8S△ADE≤8,
所以12≤S≤8,
所以此八面体的表面积S的取值范围为[12,8].
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
