3.1.1椭圆及其标准方程 课件(共15张ppt)
文档属性
| 名称 | 3.1.1椭圆及其标准方程 课件(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
椭圆及其标准方程
一、引入
水杯直立时,其液面形状为何形状?
水杯倾斜时,其液面形状为何形状?
发现圆与椭圆存在一定联系,学习椭圆时应先回顾圆。
二、合作探究,形成概念
1.利用手中的细线,如何绘制出圆?
取一细线让两端重合(端点记为 ),套上笔尖,拉紧细线移动笔尖(动点),画出的轨迹即为圆。
2.如果让两端分开一段距离(端点记为 ),套上笔尖,拉紧细线移动笔尖(动点),画出的轨迹?
椭圆
(一)探究思考
二、合作探究,形成概念
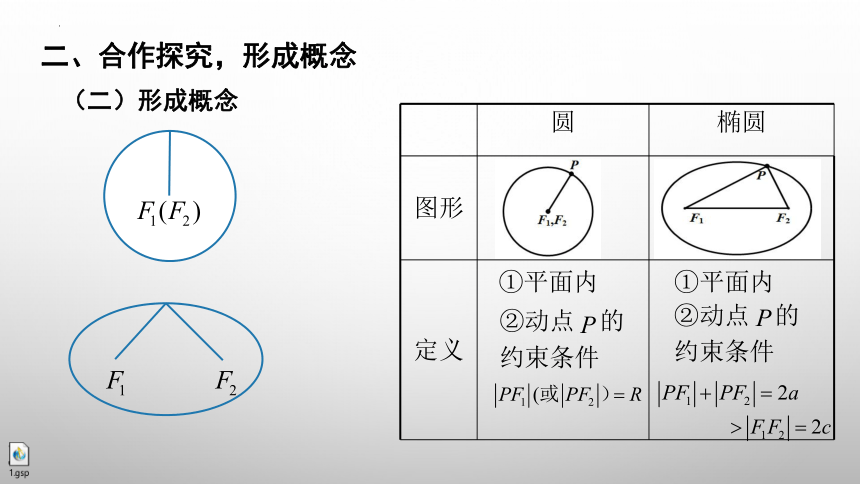
(二)形成概念
圆 椭圆
图形
定义
①平面内
②动点 的
约束条件
②动点 的
约束条件
①平面内
二、合作探究,形成概念
(二)形成概念
椭圆的定义:平面内与两个定点 的距离的和等于常数(记作 ) 的点的轨迹叫做椭圆,
这两个定点叫做椭圆的焦点
两焦点的距离叫做椭圆的焦距
椭圆
线段
不存在
求曲线的方程(轨迹方程),一般有几个步骤:
三、深化研究,构建方程
(一)回顾点的轨迹方程求法
1.建系、设标
2.写出几何条件并用坐标表示
3.化简并检验
三、深化研究,构建方程
(二)类比学习,大胆猜测
1.圆
2.椭圆
三、深化研究,构建方程
(三)实践计算,小心求证
解:建立如图坐标系;
设出曲线上动点
限制条件
列出方程
即:
三、深化研究,构建方程
(三)实践计算,小心求证
椭圆的标准方程:
三、深化研究,构建方程
椭圆 焦点在 轴上 焦点在 轴上
图形
定义 ①平面内 ②动点 的约束条件 ①平面内
②动点 的约束条件
方程
1.已知椭圆焦点坐标分别为 ,并经过点 ,
求其标准方程。
四、应用拓展,能力提升
五、课堂小结,提升经验
椭圆 焦点在 轴上 焦点在 轴上
图形
定义 ①平面内 ②动点 的约束条件 方程
焦点
关系 六、课后作业
作业
练习B 第1、3、4
椭圆及其标准方程
一、引入
水杯直立时,其液面形状为何形状?
水杯倾斜时,其液面形状为何形状?
发现圆与椭圆存在一定联系,学习椭圆时应先回顾圆。
二、合作探究,形成概念
1.利用手中的细线,如何绘制出圆?
取一细线让两端重合(端点记为 ),套上笔尖,拉紧细线移动笔尖(动点),画出的轨迹即为圆。
2.如果让两端分开一段距离(端点记为 ),套上笔尖,拉紧细线移动笔尖(动点),画出的轨迹?
椭圆
(一)探究思考
二、合作探究,形成概念
(二)形成概念
圆 椭圆
图形
定义
①平面内
②动点 的
约束条件
②动点 的
约束条件
①平面内
二、合作探究,形成概念
(二)形成概念
椭圆的定义:平面内与两个定点 的距离的和等于常数(记作 ) 的点的轨迹叫做椭圆,
这两个定点叫做椭圆的焦点
两焦点的距离叫做椭圆的焦距
椭圆
线段
不存在
求曲线的方程(轨迹方程),一般有几个步骤:
三、深化研究,构建方程
(一)回顾点的轨迹方程求法
1.建系、设标
2.写出几何条件并用坐标表示
3.化简并检验
三、深化研究,构建方程
(二)类比学习,大胆猜测
1.圆
2.椭圆
三、深化研究,构建方程
(三)实践计算,小心求证
解:建立如图坐标系;
设出曲线上动点
限制条件
列出方程
即:
三、深化研究,构建方程
(三)实践计算,小心求证
椭圆的标准方程:
三、深化研究,构建方程
椭圆 焦点在 轴上 焦点在 轴上
图形
定义 ①平面内 ②动点 的约束条件 ①平面内
②动点 的约束条件
方程
1.已知椭圆焦点坐标分别为 ,并经过点 ,
求其标准方程。
四、应用拓展,能力提升
五、课堂小结,提升经验
椭圆 焦点在 轴上 焦点在 轴上
图形
定义 ①平面内 ②动点 的约束条件 方程
焦点
关系 六、课后作业
作业
练习B 第1、3、4
