广东省两阳中学2023-2024学年高二下学期月考一数学试题(PDF版,含解析)
文档属性
| 名称 | 广东省两阳中学2023-2024学年高二下学期月考一数学试题(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 476.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 11:44:38 | ||
图片预览




文档简介
广东两阳中学 2023-2024 学年度第二学期月考一
高二数学
(时间:120 分钟 分值:150 分)
班别 学号 姓名
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每个小题给出的四个选项中,只有一
项是符合题目要求的.
1.直线 3x y 3 0的倾斜角为( )
π
A. π 2π 5π
6 B. C. D.3 3 6
2.把 5个相同的小球分给 3个小朋友,使每个小朋友都能分到小球的分法有( )
A.4种 B.6种 C.21种 D.35种
3.如图,在三棱锥P ABC中,点 N为棱 AP的中点,点M 在棱BC上,
且满足CM 2BM,设 PA a,PB b,PC c,则MN ( )
1 2 1 1 2 a b c a b 1
A. B. c
2 3 3 2 3 3
1 2 1 1 2 1
C. a b c D. a b c
2 3 3 2 3 3
4.数学家杨辉在其专著《详解九章算术法》和《算法通变本末》中,提出了一些新的高阶等差数
列,其中二阶等差数列是一个常见的高阶等差数列,如数列 2,4,7,11,16,从第二项起,每
一项与前一项的差组成新数列 2,3,4,5,新数列 2,3,4,5为等差数列,则称数列 2,4,7,
11,16为二阶等差数列.现有二阶等差数列 an ,其中前几项分别为 2,5,9,14,20,27,记
该数列的后一项与前一项之差组成新数列 bn ,则b8 ( )
A.8 B.9 C.10 D.11
5. 1 x 1 2x 5 的展开式中 x2的系数为( )
A.-40 B.-10 C.40 D.30
6.如图,已知圆柱OO1的轴截面 AA1B1B为矩形, AB 2AA1,P,Q
1
分别为圆柱上、下底面圆周上一点, A P P 1 B2 1
, AQ 2Q B,则异
面直线 PQ与 AB所成角的余弦值为( )
试卷第 1页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
1
A. B 3 2 3. C. D.
3 3 2 2
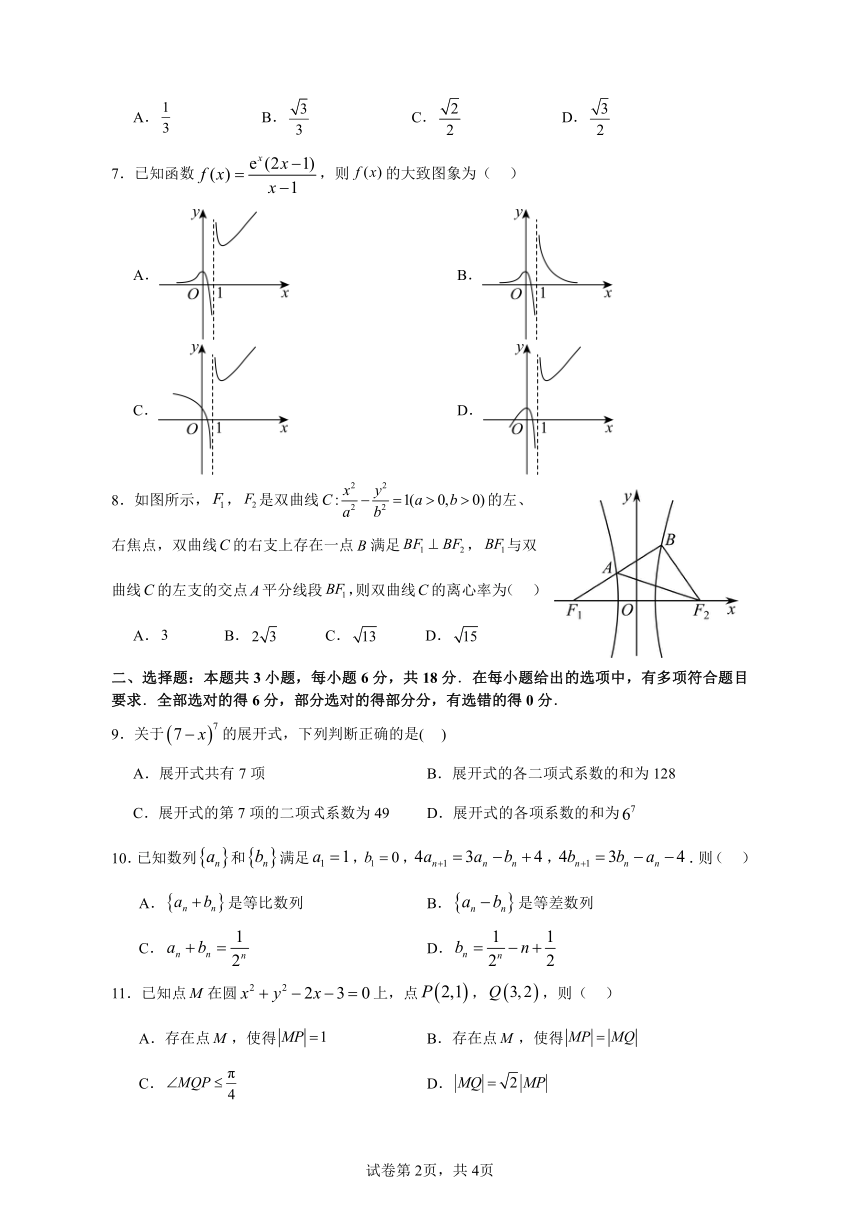
ex (2x 1)
7.已知函数 f (x) ,则 f (x)的大致图象为( )
x 1
A. B.
C. D.
2 2
8.如图所示,F1, F2是双曲线C :
x y
2 2 1(a 0,b 0)的左、a b
右焦点,双曲线C的右支上存在一点 B满足 BF1 BF2, BF1与双
曲线C的左支的交点A平分线段 BF1,则双曲线C的离心率为( )
A.3 B. 2 3 C. 13 D. 15
二、选择题:本题共 3 小题,每小题 6 分,共 18 分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6 分,部分选对的得部分分,有选错的得 0 分.
7 x 79.关于 的展开式,下列判断正确的是( )
A.展开式共有 7项 B.展开式的各二项式系数的和为 128
C.展开式的第 7项的二项式系数为 49 D.展开式的各项系数的和为67
10.已知数列 an 和 bn 满足 a1 1,b1 0,4an 1 3an bn 4,4bn 1 3bn an 4.则( )
A. an bn 是等比数列 B. an bn 是等差数列
a b 1 b 1 1C. n n n D.2 n
2n
n
2
11.已知点M 在圆 x2 y2 2x 3 0上,点P 2,1 ,Q 3, 2 ,则( )
A.存在点M ,使得 MP 1 B.存在点M ,使得 MP MQ
C. MQP
π
D. MQ 2 MP
4
试卷第 2页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12.抛物线 2y2 x的焦点坐标为 .
13.在等比数列 an 中, a2 3,a 81 25 , Sn为该数列的前 n项和,Tn为数列 an 的前 n项和,
且Tn tS2n,则实数 t的值是 .
14.已知 f (x) (x 1)ex,若对任意 x1,x2 [ 3,0],都有 f (x1) f (x2 ) t,则实数 t的取值
范围是 .
四、解答题:本大题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
设 an 是正项等差数列, a3 3,且 a2 ,a5 1,a6 2成等比数列.
(1)求 an 的通项公式;
(2)记 an 的前 n项和为 Sn,且b
1
n S ,求数列 bn 的前 n项和Tn.n
16.(15分)
如图,在四棱锥 P ABCD中,底面 ABCD是正方形,侧棱 PD
底面 ABCD,PD DC 1,E是 PC的中点,作EF PB交 PB
于点 F.
(1)求证: PB 平面 EFD;
(2)求平面CPB与平面 PBD的夹角的大小.
17.(15分)
3 2
已知函数 f x x ax bx c a,b,c R ,且 1,1是函数 f x 的两个极值点.
(1)求 a与b的值;
(2)若函数 f x 在 2,2 上有最小值为 2,在 2,m 上有最大值,求m的取值范围.
试卷第 3页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
18.(17分)
已知函数 f x ax 1 ln x a R ,
1
(1)当 a 时,求函数 f x 在 1,e 上的最大值和最小值;
2
(2)讨论函数 f x 的单调性;
(3)若曲线 y f x 在点 1, f 1 处的切线与 y 轴垂直,不等式 f x bx 2对 x 0, 恒成立,
求实数b的取值范围.
19.(17分)
在平面直角坐标系 xOy中,已知点 F1( 3,0),F2 ( 3,0), MF1 MF2 4,记M 的轨迹为C.
(1)求C的方程;
(2)过点 1,0 的直线 l与C交于 P,Q两点, A 2,0 , B 2,0 ,设直线 AP,BP,BQ的斜率分别
为 k1,k2 ,k3.
(i 3)若 k ,求 k2 3;2
(ii)证明: k2 k1 k3 为定值.
试卷第 4页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
广东两阳中学 2023-2024 学年度第二学期月考一
高二数学 参考答案
班别 学号 姓名
1.B【分析】由直线的斜率计算倾斜角.
【详解】直线 3x y 3 0改写为斜截式方程为 y 3x 3,所以直线斜率 k 3,则直线倾斜
π
角为 .故选:B
3
2.B【分析】元素相同问题用隔板法.
2
【详解】利用隔板法:由题可知使每个小朋友都能分到小球的分法有C4 6种.故选:B .
3.A【分析】根据空间向量基本定理结合空间向量的线性运算即可得解.
【详解】因为点 N为棱 AP的中点,CM 2BM,设 PA a,PB b,PC c,所以
1 MN MB BP PN CB PB 1
PA
3 2
1 PB PC PB 1 1 PA PA 2 PB 1 1 2 1 PC a b c .故选:A.3 2 2 3 3 2 3 3
4.C【分析】根据概念,先写出等差数列 bn 的前几项,得到通项公式,再求数列的第 8项.
【详解】由题意,数列 bn 的前几项为:3,4,5,6,7,且数列 bn 为等差数列,所以:bn n 2,
故b8 8 2 10 .故选:C.
5 D r r r. 【分析】利用二项式展开式的通项公式C5 ( 2) x 即可求解.
1 2x 5 C r ( 2)r r【详解】根据题意知, 的展开式的通项公式为 5 x ,
2 2 1 1
∴展开式中含 x2项的系数为C5 ( 2) C5 ( 2) 30 .故选:D.
【点睛】本题考查了二项式定理的展开式、求二项式展开式的系数,属于基础题.
6.C【分析】建立空间直角坐标系,设 AB 2AA1 6,根据已知得出 AB 0,6,0 ,PQ 0,3, 3 ,
即可根据异面直线夹角的向量求法得出答案.
【详解】如图,以 A为坐标原点建立空间直角坐标系,设
AB 2AA1 6,则 A 0,0,0 , B 0,6,0
1
,结合 A1P P B2 1
,
AQ 2Q
3 3 3 3 3 9
B,可得 P , ,32 2 ,
Q , , 0 ,所以 AB 0,6,0 ,
3 2
答案第 1页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
PQ 0,3, 3 AB PQ 18 2 ,所以异面直线 PQ与 AB所成角的余弦值为 ,故选:C.
AB PQ 6 3 2 2
7.A【分析】利用导数判定单调性结合特殊区间即可得出选项.
x x 2
【详解】 f (x)
e (2x 1)
, f x e (2x 3x) 3
x 1 2 ,令
f x 0 x ,0 , ,所以x 1 2
f x 在 , 0 3 , 和 上单调递增,又当 x 0时, x 1 0,2x 1 0,ex 0, f (x) 0 .故选:
2
A
8.C【分析】设 AB AF1 x(x 0),由双曲线的定义可求得 BF1 2x, BF2 2x 2a,
AF2 x 2a,利用勾股定理求得 x 3a,在△BF F a,c1 2中利用勾股定理即可求得 的关系式,从
而求得答案.
【详解】设 AB AF1 x(x 0),由双曲线的定义得 BF1 2x, BF2 2x 2a, AF2 x 2a,
BF BF AF |2 AB |2由 1 2得 2 | BF2 |
2, (x 2 a) 2 x2 (2 x 2 a) 2,解得 x 3a,所以 BF1 6a,
BF 2 2 2 2 2 22 4a,在△BF1F2中,由勾股定理得 F1F2 | BF1 | | BF2 | , (2c) (6a) (4a) ,
2
整理得 c2 13a2 ,即双曲线C的离心率 e c 13 ,故选:C.
a2
9.BD【分析】根据二项式定理的性质逐项判断即可.
【详解】展开式共有7 1 8项,故 A错误.展开式的各二项式系数的和为27 128,故 B正确.
6 1 7
展开式的第 7项的二项式系数为C7 C7 7,故 C错误.展开式的各项系数的和为 7 1 67,
故 D正确.故选:BD.
10.ABD【分析】将已知的两式相加、相减可得有关结论.
4an 1 3an bn 4① an 1 bn 1 1
【详解】由已知: ,① ②得:4 an 1 bn 1 2 an bn
4bn 1 3bn an 4② a
且
n bn 2
a1 b
1
1 1,所以 an bn 是以1为首项, 为公比的等比数列.故 A正确,且 an b
1
n n 1 ③2 2
故 C错误;① ②得: 4 an 1 bn 1 4 an bn 8 an 1 bn 1 an bn 2且 a1 b1 1,
所以 an bn 是以1为首项, 2为公差的等差数列.故 B正确,且 an bn 2n 1④
1 1 1
③ - ④得: 2bn n 1 2n 1 bn n n ,故 D正确.故选:ABD2 2 2
11.ACD
答案第 2页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
【分析】利用圆心C的坐标,及半径的大小,可求得 CP 的范围,继而判定选项 A;设M x, y ,
利用坐标验证 MQ 2 MP ,继而可判定选项 B,D;结合题中条件可知当QM 与圆相切时,
MQP最大,解出即可判定选项 C.
【详解】圆 x2 y2 2x 3 0化为 x 1 2 y2 4,其圆心C 1,0 ,半径 r 2,又 P 2,1 ,则
CP 2 1 2 1 0 2 2,因为点M 在圆上,所以 MP 2 2, 2 2 ,
所以存在点M ,使得 MP 1,故 A正确;
2 2 2 2 2
设M x, y ,若 MQ 2 MP ,则 MQ 2 MP 2,即 x 3 y 2 2 x 2 y 1 ,
化为 x2 y2 2x 3 0,又点M 在圆 x2 y2 2x 3 0上,故
MQ 2 MP 一定成立,则 B错,D正确;
k 1 0 1,k 2 0又 PC QC 1,则C,P,Q三点共线,且2 1 3 1
CP 2 r CQ 3 1 2, 2 0 2 2 2 r,则当QM 与圆
MQP π π相切时, 最大,此时 MQP ,故 MQP ,故 C正确,故选:ACD.
4 4
1
12. ,0
【分析】把抛物线方程化成标准形式后可求焦点坐标.
8
2 1 1 1 1
【详解】抛物线的标准方程为: y x p
,故 ,故焦点坐标为 ,0 .故答案为: ,02 4
.
8 8
1
13. /0.25【分析】根据等比数列的通项公式求得公比后,利用等比数列的前 n项和公式建立方
4
程,解出即可.
a 81
【详解】设数列 a q 5 27 q3 n 2 n 1n 的公比为 ,则 q 3 a 1a2 3
,解得 ,故 an a2q 3 , 1 ,
S 1 3
n 1 9n n2
所以 n , S2n ,又 an 9
n 1 1 9
,则Tn ,1 3 1 3 1 9
n n
由Tn tS
1 9 1 9 1 1
2n得, t ,解得 t ,故答案为: .1 9 1 3 4 4
1
14.[1 2 , )【分析】对 f (x)求导,求出 f (x)的最值,由任意x ,x2 [ 3 ,0],都有 | f (x1) f (x2 ) |≤ t1 ,e
可得 t f x f xmax min ,再求出 t的范围即可.
x x
【详解】由 f x x 1 e ,得 f x x 2 e ,令 f (x) 0,则 x 2,
所以当 3 x 2时, f (x) 0;当 2 x 0时, f (x) 0,
所以 f (x)在 [ 3, 2]上单调减,在[ 2, 0]上单调增,
答案第 3页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
f 1所以 2 2 , f 3
2
3 , f 0 1
1
,所以 f x f 2 , f x f 0 1
e e min
2 e max ,
1
因为对任意x , x2 [ 3, 0]1 ,都有 | f (x1) f (x2 ) |≤ t,所以只需 t f x f x 1 max min ,e2
1 1
所以实数 t的取值范围为[1 2 , ).故答案为:[1 e e2
, ).
15.【详解】(1)设正项等差数列 an 的公差为d ,则 a1 0,d 0, 1分
a3 3
由题意,可得 2 , 2分
a5 1 a2 a6 2
a1 2d 3
即 , 4分
a1 4d 1
2
a1 d a1 5d 2
43
a1 1
a
1 7
解得 或 (舍去), 6分
d 1 d 11
7
故 an 的通项公式 an 1 n 1 n . 7分
n 1 n
(2)由(1),可得 an n,Sn , 8分2
b 1 2 2 1 1则 n
Sn n n 1 n n 1
, 10分
T b b b 2 1 1 1 1 1 1 1 2n故 n 1 2 n
2
1
2 2 3 n n 1
, 12分
n 1 n 1
2n
即数列 bn 的前 n项和Tn . 13分n 1
16.【详解】(1)解法一:因为底面 ABCD是正方形,侧棱PD 底面 ABCD,
以 D为原点,DA,DC,DP所在直线分别为 x轴,y轴,z轴,
建立空间直角坐标系, 1分
依意得 A(1,0,0),B(1,1,0),P(0,0,1) E 0, 1 , 1 , , 2分
2 2
1 1
所以 PB (1,1, 1),DE 0, , , 3分
2 2
因为 PB
1 1
DE 0 0,所以 PB ED, 5分
2 2
由已知 EF PB,且 EF DE E, EF 平面 EFD,DE 平面 EFD,
所以 PB 平面 EFD. 7分
解法二: 底面 ABCD是正方形, BC CD,
PD 底面 ABCD,且 BC 平面 ABCD, PD BC,
答案第 4页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
PD CD D, PD 平面 PCD,CD 平面 PCD,
BC 平面 PCD, 2分
DE 平面 PCD, BC DE,
PD DC 1,E为PC中点, DE PC,
BC PC C,BC 平面 PBC, PC 平面 PBC,
DE 平面 PBC, 4分
PB 平面 PBC, DE PB, 5分
由已知 EF PB,且 EF DE E, EF 平面 EFD,DE 平面 EFD,
所以 PB 平面 EFD . 7分
(2)依题意得C (0,1, 0),且CB (1,0,0), PC (0,1, 1),
n 设平面CPB的一个法向量为 (x, y, z),
CB n x 0, x 0,
则 ,即 取 n (0,1,1), 9分
PC n y z 0, z y,
因为DB (1,1,0), DP (0, 0,1),设平面 PBD的一个法向量为m a,b,c ,
DB
m a b 0, a b
m 则 即 取 (1, 1,0), 11分
DP m c 0, c 0
n m 1
设平面CPB与平面 PBD的夹角为 ,则 cos cos n,m , 13分n m 2
又 0,
π π π
,所以 ,所以平面CPB与平面 PBD的夹角为 . 15分 2 3 3
17 3.【详解】(1)因为 f x x ax2 bx c,所以 f x 3x2 2ax b, 1分
由条件知 f 1 f 1 0, 2分
3 2a b 0
即 , 3分
3 2a b 0
解得 a 0,b 3,经检验适合题意(1分); 5分
所以 a与b的值分别为0和 3 6分
(2)由(1)可知 f x x3 3x c,则 f x 3x 2 3, 7分
令 f x 0,得 x= 1或 x 1,
f x 和 f x 随 x的变化情况如下表:
答案第 5页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
x -2 2, 1 -1 1,1 1 1, 2 2
f x + 0 — 0 +
f x c 2 单调递增 极大值 单调递减 极小值 单调递增 c 2
10分
因为 f 2 c 2, f 2 c 2, f 1 c 2,
所以函数 f x 在 2,2 上的最小值为 f 1 c 2,
所以 c 2 2,解得 c = 0,
3
所以 f x x 3x, 11分
因为函数在 , 1 和 1, 上递增,在 1,1 上递减,且 f 1 f 2 2,
画出函数图象如图所示, 13分
由于函数在区间 2,m 上有最大值,根据图象可知m xB , xA ,即m 1,2 . 15分
1 1
18.【详解】(1)当 a 时, f x x 1 ln x f x 1 1 ,所以 , 1分
2 2 2 x
令 f x 0时, x 2,
当 x 2时, f (x) 0,当0 x 2时, f (x) 0, 3分
∵ x 1,e ,所以 f x 1 x 1 ln x在 x 2取得极小值,也是最小值,
2
∴ f x f 2 ln 2min , 4分
1
又 f 1 , f e e e 4 1 2
2 2 2 2
f (x)max f (1)
1
5分
2
∴ f x 1在 1,e 上的最大值为 ,最小值是 ln 2; 6分
2
1 ax 1
(2) f x a x 0 7分
x x
当 a 0时,令 f (x) 0
1
,解得: x ,
a
令 f x 0 1,解得:0 x ,
a
所以 f x 在 0,
1 1
单调递减,在 ,
单调递增, 9分
a a
答案第 6页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
当 a 0时, f x 1 0在 0, 上恒成立,
x
所以 f x 在 0, 上为减函数,
ax 1
当 a<0时, f x 0在 0, 恒成立,
x
所以 f x 在 0, 上单调递减. 11分
a 0 f x 0, 1 1综上,当 时, 在 单调递减,在 ,
单调递增,
a a
当 a 0时, f x 在 0, 上单调递减. 12分
(3) f x a 1 ,依题意: f 1 a 1 0,解得: a 1, 13分
x
所以 f x x 1 ln x,
又 f x bx 2对 x 0, 恒成立,即 x 1 ln x bx 2,
1 ln x
所以b 1 在 0, 上恒成立. 14分
x x
g(x) 1 ln x令 1(x 0) , g (x)
ln x 2
x x2
,
2 1
当 0 x e2时 g (x) 0,当 x e2 时 g (x) 0,∴ x e2 时 g x g(e ) 1 min 2 , 16分e
故b 1
1
,
e2
所以b 的取值范围为 ,1
1
2 . 17分 e
19.【详解】(1)因为 MF1 MF2 4 2 3,
根据椭圆的定义可知曲线C为以 F1( 3,0),F2 ( 3,0)为焦点的椭圆, 2分
其中 a 2,c 3, 4分
x2
所以椭圆方程: y2 1. 5分
4
(2) (i)易知直线 PQ的斜率不为零,
所以设直线 PQ的方程为 x my 1,P x1, y1 ,Q x2 , y2 , 6分
x my 1
2 2 ,得 m2 4 y2 2my 3 0, 7分
x 4y 4
2 2 2
则Δ 2m 4 m 4 ( 3) 16 m 3 0 ,
答案第 7页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
y y 2m 31 2 2 , y1y2 2 , 8分m 4 m 4
k k y1 y2 y y 1 22 3 x1 2 x2 2 my1 1 my2 1
9分
y
3
2
1
y2 3
2
m 4
m y 2
,
1y2 m y1 y2 1 3m 2m 4
m2
m 1
4 m2 4
11分
k 3 32 , k3 . 12分2 2
x21
2 1
(ii)因为 k k y1 y1 y1 4 1 , 15分1 2 x1 2 x 2 x
2
1 1 4 x
2
1 4 4
k k k k k k k 1 3 2 1 3 1 2 2 3 1为定值. 17分4 4
答案第 8页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
高二数学
(时间:120 分钟 分值:150 分)
班别 学号 姓名
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每个小题给出的四个选项中,只有一
项是符合题目要求的.
1.直线 3x y 3 0的倾斜角为( )
π
A. π 2π 5π
6 B. C. D.3 3 6
2.把 5个相同的小球分给 3个小朋友,使每个小朋友都能分到小球的分法有( )
A.4种 B.6种 C.21种 D.35种
3.如图,在三棱锥P ABC中,点 N为棱 AP的中点,点M 在棱BC上,
且满足CM 2BM,设 PA a,PB b,PC c,则MN ( )
1 2 1 1 2 a b c a b 1
A. B. c
2 3 3 2 3 3
1 2 1 1 2 1
C. a b c D. a b c
2 3 3 2 3 3
4.数学家杨辉在其专著《详解九章算术法》和《算法通变本末》中,提出了一些新的高阶等差数
列,其中二阶等差数列是一个常见的高阶等差数列,如数列 2,4,7,11,16,从第二项起,每
一项与前一项的差组成新数列 2,3,4,5,新数列 2,3,4,5为等差数列,则称数列 2,4,7,
11,16为二阶等差数列.现有二阶等差数列 an ,其中前几项分别为 2,5,9,14,20,27,记
该数列的后一项与前一项之差组成新数列 bn ,则b8 ( )
A.8 B.9 C.10 D.11
5. 1 x 1 2x 5 的展开式中 x2的系数为( )
A.-40 B.-10 C.40 D.30
6.如图,已知圆柱OO1的轴截面 AA1B1B为矩形, AB 2AA1,P,Q
1
分别为圆柱上、下底面圆周上一点, A P P 1 B2 1
, AQ 2Q B,则异
面直线 PQ与 AB所成角的余弦值为( )
试卷第 1页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
1
A. B 3 2 3. C. D.
3 3 2 2
ex (2x 1)
7.已知函数 f (x) ,则 f (x)的大致图象为( )
x 1
A. B.
C. D.
2 2
8.如图所示,F1, F2是双曲线C :
x y
2 2 1(a 0,b 0)的左、a b
右焦点,双曲线C的右支上存在一点 B满足 BF1 BF2, BF1与双
曲线C的左支的交点A平分线段 BF1,则双曲线C的离心率为( )
A.3 B. 2 3 C. 13 D. 15
二、选择题:本题共 3 小题,每小题 6 分,共 18 分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6 分,部分选对的得部分分,有选错的得 0 分.
7 x 79.关于 的展开式,下列判断正确的是( )
A.展开式共有 7项 B.展开式的各二项式系数的和为 128
C.展开式的第 7项的二项式系数为 49 D.展开式的各项系数的和为67
10.已知数列 an 和 bn 满足 a1 1,b1 0,4an 1 3an bn 4,4bn 1 3bn an 4.则( )
A. an bn 是等比数列 B. an bn 是等差数列
a b 1 b 1 1C. n n n D.2 n
2n
n
2
11.已知点M 在圆 x2 y2 2x 3 0上,点P 2,1 ,Q 3, 2 ,则( )
A.存在点M ,使得 MP 1 B.存在点M ,使得 MP MQ
C. MQP
π
D. MQ 2 MP
4
试卷第 2页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12.抛物线 2y2 x的焦点坐标为 .
13.在等比数列 an 中, a2 3,a 81 25 , Sn为该数列的前 n项和,Tn为数列 an 的前 n项和,
且Tn tS2n,则实数 t的值是 .
14.已知 f (x) (x 1)ex,若对任意 x1,x2 [ 3,0],都有 f (x1) f (x2 ) t,则实数 t的取值
范围是 .
四、解答题:本大题共 5 小题,共 77 分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
设 an 是正项等差数列, a3 3,且 a2 ,a5 1,a6 2成等比数列.
(1)求 an 的通项公式;
(2)记 an 的前 n项和为 Sn,且b
1
n S ,求数列 bn 的前 n项和Tn.n
16.(15分)
如图,在四棱锥 P ABCD中,底面 ABCD是正方形,侧棱 PD
底面 ABCD,PD DC 1,E是 PC的中点,作EF PB交 PB
于点 F.
(1)求证: PB 平面 EFD;
(2)求平面CPB与平面 PBD的夹角的大小.
17.(15分)
3 2
已知函数 f x x ax bx c a,b,c R ,且 1,1是函数 f x 的两个极值点.
(1)求 a与b的值;
(2)若函数 f x 在 2,2 上有最小值为 2,在 2,m 上有最大值,求m的取值范围.
试卷第 3页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
18.(17分)
已知函数 f x ax 1 ln x a R ,
1
(1)当 a 时,求函数 f x 在 1,e 上的最大值和最小值;
2
(2)讨论函数 f x 的单调性;
(3)若曲线 y f x 在点 1, f 1 处的切线与 y 轴垂直,不等式 f x bx 2对 x 0, 恒成立,
求实数b的取值范围.
19.(17分)
在平面直角坐标系 xOy中,已知点 F1( 3,0),F2 ( 3,0), MF1 MF2 4,记M 的轨迹为C.
(1)求C的方程;
(2)过点 1,0 的直线 l与C交于 P,Q两点, A 2,0 , B 2,0 ,设直线 AP,BP,BQ的斜率分别
为 k1,k2 ,k3.
(i 3)若 k ,求 k2 3;2
(ii)证明: k2 k1 k3 为定值.
试卷第 4页,共 4页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
广东两阳中学 2023-2024 学年度第二学期月考一
高二数学 参考答案
班别 学号 姓名
1.B【分析】由直线的斜率计算倾斜角.
【详解】直线 3x y 3 0改写为斜截式方程为 y 3x 3,所以直线斜率 k 3,则直线倾斜
π
角为 .故选:B
3
2.B【分析】元素相同问题用隔板法.
2
【详解】利用隔板法:由题可知使每个小朋友都能分到小球的分法有C4 6种.故选:B .
3.A【分析】根据空间向量基本定理结合空间向量的线性运算即可得解.
【详解】因为点 N为棱 AP的中点,CM 2BM,设 PA a,PB b,PC c,所以
1 MN MB BP PN CB PB 1
PA
3 2
1 PB PC PB 1 1 PA PA 2 PB 1 1 2 1 PC a b c .故选:A.3 2 2 3 3 2 3 3
4.C【分析】根据概念,先写出等差数列 bn 的前几项,得到通项公式,再求数列的第 8项.
【详解】由题意,数列 bn 的前几项为:3,4,5,6,7,且数列 bn 为等差数列,所以:bn n 2,
故b8 8 2 10 .故选:C.
5 D r r r. 【分析】利用二项式展开式的通项公式C5 ( 2) x 即可求解.
1 2x 5 C r ( 2)r r【详解】根据题意知, 的展开式的通项公式为 5 x ,
2 2 1 1
∴展开式中含 x2项的系数为C5 ( 2) C5 ( 2) 30 .故选:D.
【点睛】本题考查了二项式定理的展开式、求二项式展开式的系数,属于基础题.
6.C【分析】建立空间直角坐标系,设 AB 2AA1 6,根据已知得出 AB 0,6,0 ,PQ 0,3, 3 ,
即可根据异面直线夹角的向量求法得出答案.
【详解】如图,以 A为坐标原点建立空间直角坐标系,设
AB 2AA1 6,则 A 0,0,0 , B 0,6,0
1
,结合 A1P P B2 1
,
AQ 2Q
3 3 3 3 3 9
B,可得 P , ,32 2 ,
Q , , 0 ,所以 AB 0,6,0 ,
3 2
答案第 1页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
PQ 0,3, 3 AB PQ 18 2 ,所以异面直线 PQ与 AB所成角的余弦值为 ,故选:C.
AB PQ 6 3 2 2
7.A【分析】利用导数判定单调性结合特殊区间即可得出选项.
x x 2
【详解】 f (x)
e (2x 1)
, f x e (2x 3x) 3
x 1 2 ,令
f x 0 x ,0 , ,所以x 1 2
f x 在 , 0 3 , 和 上单调递增,又当 x 0时, x 1 0,2x 1 0,ex 0, f (x) 0 .故选:
2
A
8.C【分析】设 AB AF1 x(x 0),由双曲线的定义可求得 BF1 2x, BF2 2x 2a,
AF2 x 2a,利用勾股定理求得 x 3a,在△BF F a,c1 2中利用勾股定理即可求得 的关系式,从
而求得答案.
【详解】设 AB AF1 x(x 0),由双曲线的定义得 BF1 2x, BF2 2x 2a, AF2 x 2a,
BF BF AF |2 AB |2由 1 2得 2 | BF2 |
2, (x 2 a) 2 x2 (2 x 2 a) 2,解得 x 3a,所以 BF1 6a,
BF 2 2 2 2 2 22 4a,在△BF1F2中,由勾股定理得 F1F2 | BF1 | | BF2 | , (2c) (6a) (4a) ,
2
整理得 c2 13a2 ,即双曲线C的离心率 e c 13 ,故选:C.
a2
9.BD【分析】根据二项式定理的性质逐项判断即可.
【详解】展开式共有7 1 8项,故 A错误.展开式的各二项式系数的和为27 128,故 B正确.
6 1 7
展开式的第 7项的二项式系数为C7 C7 7,故 C错误.展开式的各项系数的和为 7 1 67,
故 D正确.故选:BD.
10.ABD【分析】将已知的两式相加、相减可得有关结论.
4an 1 3an bn 4① an 1 bn 1 1
【详解】由已知: ,① ②得:4 an 1 bn 1 2 an bn
4bn 1 3bn an 4② a
且
n bn 2
a1 b
1
1 1,所以 an bn 是以1为首项, 为公比的等比数列.故 A正确,且 an b
1
n n 1 ③2 2
故 C错误;① ②得: 4 an 1 bn 1 4 an bn 8 an 1 bn 1 an bn 2且 a1 b1 1,
所以 an bn 是以1为首项, 2为公差的等差数列.故 B正确,且 an bn 2n 1④
1 1 1
③ - ④得: 2bn n 1 2n 1 bn n n ,故 D正确.故选:ABD2 2 2
11.ACD
答案第 2页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
【分析】利用圆心C的坐标,及半径的大小,可求得 CP 的范围,继而判定选项 A;设M x, y ,
利用坐标验证 MQ 2 MP ,继而可判定选项 B,D;结合题中条件可知当QM 与圆相切时,
MQP最大,解出即可判定选项 C.
【详解】圆 x2 y2 2x 3 0化为 x 1 2 y2 4,其圆心C 1,0 ,半径 r 2,又 P 2,1 ,则
CP 2 1 2 1 0 2 2,因为点M 在圆上,所以 MP 2 2, 2 2 ,
所以存在点M ,使得 MP 1,故 A正确;
2 2 2 2 2
设M x, y ,若 MQ 2 MP ,则 MQ 2 MP 2,即 x 3 y 2 2 x 2 y 1 ,
化为 x2 y2 2x 3 0,又点M 在圆 x2 y2 2x 3 0上,故
MQ 2 MP 一定成立,则 B错,D正确;
k 1 0 1,k 2 0又 PC QC 1,则C,P,Q三点共线,且2 1 3 1
CP 2 r CQ 3 1 2, 2 0 2 2 2 r,则当QM 与圆
MQP π π相切时, 最大,此时 MQP ,故 MQP ,故 C正确,故选:ACD.
4 4
1
12. ,0
【分析】把抛物线方程化成标准形式后可求焦点坐标.
8
2 1 1 1 1
【详解】抛物线的标准方程为: y x p
,故 ,故焦点坐标为 ,0 .故答案为: ,02 4
.
8 8
1
13. /0.25【分析】根据等比数列的通项公式求得公比后,利用等比数列的前 n项和公式建立方
4
程,解出即可.
a 81
【详解】设数列 a q 5 27 q3 n 2 n 1n 的公比为 ,则 q 3 a 1a2 3
,解得 ,故 an a2q 3 , 1 ,
S 1 3
n 1 9n n2
所以 n , S2n ,又 an 9
n 1 1 9
,则Tn ,1 3 1 3 1 9
n n
由Tn tS
1 9 1 9 1 1
2n得, t ,解得 t ,故答案为: .1 9 1 3 4 4
1
14.[1 2 , )【分析】对 f (x)求导,求出 f (x)的最值,由任意x ,x2 [ 3 ,0],都有 | f (x1) f (x2 ) |≤ t1 ,e
可得 t f x f xmax min ,再求出 t的范围即可.
x x
【详解】由 f x x 1 e ,得 f x x 2 e ,令 f (x) 0,则 x 2,
所以当 3 x 2时, f (x) 0;当 2 x 0时, f (x) 0,
所以 f (x)在 [ 3, 2]上单调减,在[ 2, 0]上单调增,
答案第 3页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
f 1所以 2 2 , f 3
2
3 , f 0 1
1
,所以 f x f 2 , f x f 0 1
e e min
2 e max ,
1
因为对任意x , x2 [ 3, 0]1 ,都有 | f (x1) f (x2 ) |≤ t,所以只需 t f x f x 1 max min ,e2
1 1
所以实数 t的取值范围为[1 2 , ).故答案为:[1 e e2
, ).
15.【详解】(1)设正项等差数列 an 的公差为d ,则 a1 0,d 0, 1分
a3 3
由题意,可得 2 , 2分
a5 1 a2 a6 2
a1 2d 3
即 , 4分
a1 4d 1
2
a1 d a1 5d 2
43
a1 1
a
1 7
解得 或 (舍去), 6分
d 1 d 11
7
故 an 的通项公式 an 1 n 1 n . 7分
n 1 n
(2)由(1),可得 an n,Sn , 8分2
b 1 2 2 1 1则 n
Sn n n 1 n n 1
, 10分
T b b b 2 1 1 1 1 1 1 1 2n故 n 1 2 n
2
1
2 2 3 n n 1
, 12分
n 1 n 1
2n
即数列 bn 的前 n项和Tn . 13分n 1
16.【详解】(1)解法一:因为底面 ABCD是正方形,侧棱PD 底面 ABCD,
以 D为原点,DA,DC,DP所在直线分别为 x轴,y轴,z轴,
建立空间直角坐标系, 1分
依意得 A(1,0,0),B(1,1,0),P(0,0,1) E 0, 1 , 1 , , 2分
2 2
1 1
所以 PB (1,1, 1),DE 0, , , 3分
2 2
因为 PB
1 1
DE 0 0,所以 PB ED, 5分
2 2
由已知 EF PB,且 EF DE E, EF 平面 EFD,DE 平面 EFD,
所以 PB 平面 EFD. 7分
解法二: 底面 ABCD是正方形, BC CD,
PD 底面 ABCD,且 BC 平面 ABCD, PD BC,
答案第 4页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
PD CD D, PD 平面 PCD,CD 平面 PCD,
BC 平面 PCD, 2分
DE 平面 PCD, BC DE,
PD DC 1,E为PC中点, DE PC,
BC PC C,BC 平面 PBC, PC 平面 PBC,
DE 平面 PBC, 4分
PB 平面 PBC, DE PB, 5分
由已知 EF PB,且 EF DE E, EF 平面 EFD,DE 平面 EFD,
所以 PB 平面 EFD . 7分
(2)依题意得C (0,1, 0),且CB (1,0,0), PC (0,1, 1),
n 设平面CPB的一个法向量为 (x, y, z),
CB n x 0, x 0,
则 ,即 取 n (0,1,1), 9分
PC n y z 0, z y,
因为DB (1,1,0), DP (0, 0,1),设平面 PBD的一个法向量为m a,b,c ,
DB
m a b 0, a b
m 则 即 取 (1, 1,0), 11分
DP m c 0, c 0
n m 1
设平面CPB与平面 PBD的夹角为 ,则 cos cos n,m , 13分n m 2
又 0,
π π π
,所以 ,所以平面CPB与平面 PBD的夹角为 . 15分 2 3 3
17 3.【详解】(1)因为 f x x ax2 bx c,所以 f x 3x2 2ax b, 1分
由条件知 f 1 f 1 0, 2分
3 2a b 0
即 , 3分
3 2a b 0
解得 a 0,b 3,经检验适合题意(1分); 5分
所以 a与b的值分别为0和 3 6分
(2)由(1)可知 f x x3 3x c,则 f x 3x 2 3, 7分
令 f x 0,得 x= 1或 x 1,
f x 和 f x 随 x的变化情况如下表:
答案第 5页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
x -2 2, 1 -1 1,1 1 1, 2 2
f x + 0 — 0 +
f x c 2 单调递增 极大值 单调递减 极小值 单调递增 c 2
10分
因为 f 2 c 2, f 2 c 2, f 1 c 2,
所以函数 f x 在 2,2 上的最小值为 f 1 c 2,
所以 c 2 2,解得 c = 0,
3
所以 f x x 3x, 11分
因为函数在 , 1 和 1, 上递增,在 1,1 上递减,且 f 1 f 2 2,
画出函数图象如图所示, 13分
由于函数在区间 2,m 上有最大值,根据图象可知m xB , xA ,即m 1,2 . 15分
1 1
18.【详解】(1)当 a 时, f x x 1 ln x f x 1 1 ,所以 , 1分
2 2 2 x
令 f x 0时, x 2,
当 x 2时, f (x) 0,当0 x 2时, f (x) 0, 3分
∵ x 1,e ,所以 f x 1 x 1 ln x在 x 2取得极小值,也是最小值,
2
∴ f x f 2 ln 2min , 4分
1
又 f 1 , f e e e 4 1 2
2 2 2 2
f (x)max f (1)
1
5分
2
∴ f x 1在 1,e 上的最大值为 ,最小值是 ln 2; 6分
2
1 ax 1
(2) f x a x 0 7分
x x
当 a 0时,令 f (x) 0
1
,解得: x ,
a
令 f x 0 1,解得:0 x ,
a
所以 f x 在 0,
1 1
单调递减,在 ,
单调递增, 9分
a a
答案第 6页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
当 a 0时, f x 1 0在 0, 上恒成立,
x
所以 f x 在 0, 上为减函数,
ax 1
当 a<0时, f x 0在 0, 恒成立,
x
所以 f x 在 0, 上单调递减. 11分
a 0 f x 0, 1 1综上,当 时, 在 单调递减,在 ,
单调递增,
a a
当 a 0时, f x 在 0, 上单调递减. 12分
(3) f x a 1 ,依题意: f 1 a 1 0,解得: a 1, 13分
x
所以 f x x 1 ln x,
又 f x bx 2对 x 0, 恒成立,即 x 1 ln x bx 2,
1 ln x
所以b 1 在 0, 上恒成立. 14分
x x
g(x) 1 ln x令 1(x 0) , g (x)
ln x 2
x x2
,
2 1
当 0 x e2时 g (x) 0,当 x e2 时 g (x) 0,∴ x e2 时 g x g(e ) 1 min 2 , 16分e
故b 1
1
,
e2
所以b 的取值范围为 ,1
1
2 . 17分 e
19.【详解】(1)因为 MF1 MF2 4 2 3,
根据椭圆的定义可知曲线C为以 F1( 3,0),F2 ( 3,0)为焦点的椭圆, 2分
其中 a 2,c 3, 4分
x2
所以椭圆方程: y2 1. 5分
4
(2) (i)易知直线 PQ的斜率不为零,
所以设直线 PQ的方程为 x my 1,P x1, y1 ,Q x2 , y2 , 6分
x my 1
2 2 ,得 m2 4 y2 2my 3 0, 7分
x 4y 4
2 2 2
则Δ 2m 4 m 4 ( 3) 16 m 3 0 ,
答案第 7页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
y y 2m 31 2 2 , y1y2 2 , 8分m 4 m 4
k k y1 y2 y y 1 22 3 x1 2 x2 2 my1 1 my2 1
9分
y
3
2
1
y2 3
2
m 4
m y 2
,
1y2 m y1 y2 1 3m 2m 4
m2
m 1
4 m2 4
11分
k 3 32 , k3 . 12分2 2
x21
2 1
(ii)因为 k k y1 y1 y1 4 1 , 15分1 2 x1 2 x 2 x
2
1 1 4 x
2
1 4 4
k k k k k k k 1 3 2 1 3 1 2 2 3 1为定值. 17分4 4
答案第 8页,共 8页
{#{QQABQQaQggigAJBAABhCAQEgCEKQkBAACIoGRAAEIAAAyRNABAA=}#}
同课章节目录
