高中数学人教A版(2019)选择性必修1 1.4.2 第2课时 用空间向量研究线线角、线面角(含答案)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修1 1.4.2 第2课时 用空间向量研究线线角、线面角(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 784.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-03 23:37:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
用空间向量研究线线角、线面角
必备知识基础练
1.已知两条异面直线的方向向量分别是m=(-2,1,2),n=(3,-2,1),则这两条异面直线所成的角θ满足( )
A.sin θ=- B.sin θ= C.cos θ= D.cos θ=-
2.[2023·浙江杭州高二检测]在直三棱柱ABC A′B′C′中,侧棱长为4,底面是边长为4的正三角形,则异面直线AB′与BC′所成角的余弦值为( )
A. B. C. D.
3.在正方体ABCD A1B1C1D1中,BD与平面A1C1D所成角的正弦值是( )
A. B. C. D.1
4.已知在四棱锥P ABCD中,PA⊥平面ABCD,底面ABCD是边长为4的正方形,PA=6,E为棱PD的中点,则直线EC与平面PAB所成角的正弦值为( )
A. B. C. D.
5.(多选)如图,E,F分别是正方体ABCD A1B1C1D1中棱CD上的两点,且AB=2,EF=1,则下列命题中不正确的为( )
A.异面直线B1D1与EF所成的角的大小为45°
B.异面直线B1D1与EF所成的角的大小为30°
C.直线B1D1与平面B1EF所成的角的大小为45°
D.直线B1D1与平面B1EF所成的角的大小为60°
6.[2023·福建福州高二测试]若平面α的法向量n=(-1,0,1),直线l的方向向量为d=(0,1,1),则l与α所成角的大小为________.
7.在空间直角坐标系Oxyz中,已知A(1,-2,0),B(2,1,),则直线AB与平面xOz所成的角的正弦值为________.
8.[2023·天津蓟州高二检测]在直三棱柱ABC A1B1C1中,∠BCA=90°,D1,F1分别是A1B1,A1C1的中点,BC=AC=CC1,则BD1与AF1所成角的余弦值为________.
关键能力综合练
1.将正方形ABCD沿对角线BD折起,使得平面ABD⊥平面CBD,则异面直线AB与CD所成角的余弦值为( )
A. B. C.- D.-
2.如图,在四面体OABC中,OA,OB,OC两两垂直,已知OA=OB=2,OC=1,则直线OC与平面ABC所成角的正弦值为( )
A. B. C. D.
3.[2023·湖北广水高二检测]在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,它的高为4,AA1,BB1,CC1,DD1均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为2和4,对应的圆心角为90°,则图中异面直线AB1与CD1所成角的余弦值为( )
A. B. C. D.
4.[2023·福建龙岩高二检测](多选)如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°,则( )
A.直线AD与直线BC所成角的大小为90°
B.直线AC与直线BD所成角的余弦值为
C.直线AD与平面BCD所成角的大小为45°
D.直线CD与平面ABC所成角的大小为60°
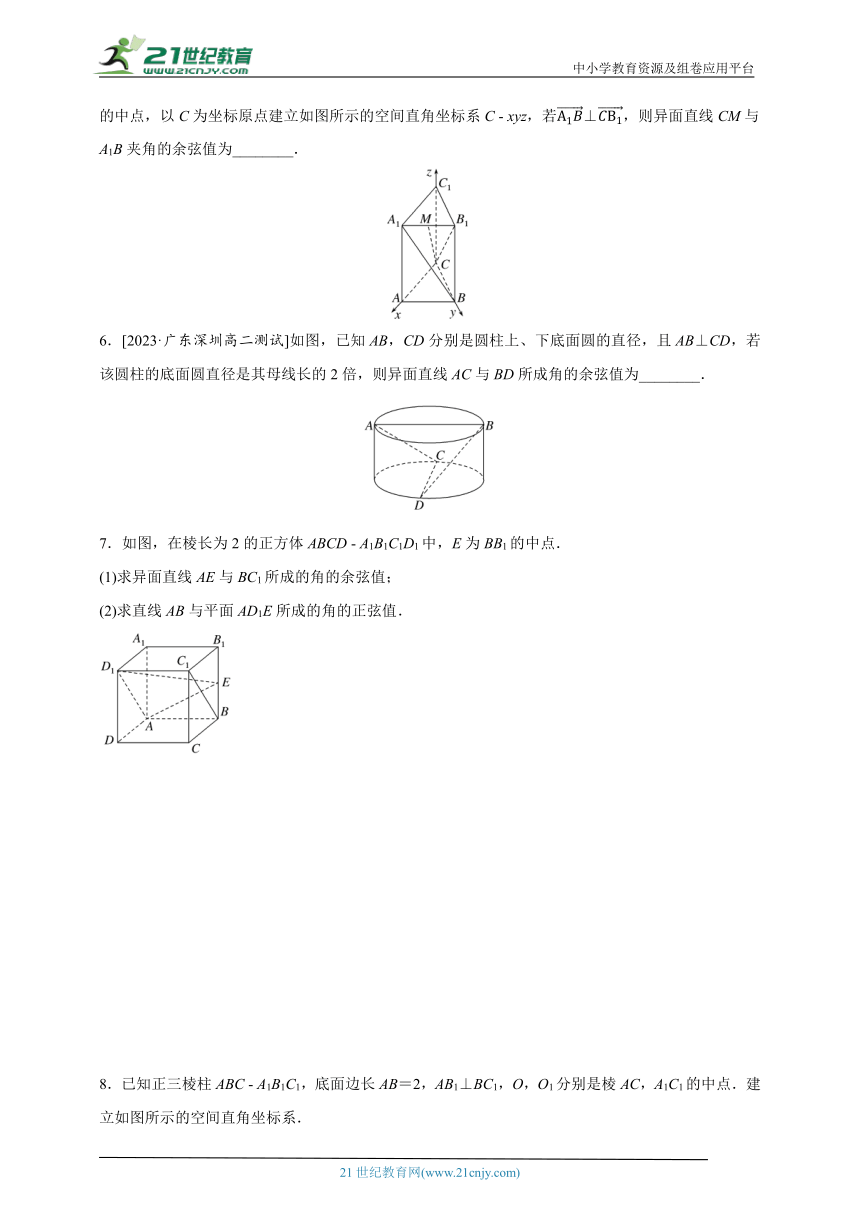
5.[2023·辽宁抚顺高二检测]在直三棱柱ABC A1B1C1中,CA=4,CB=4,∠BCA=90°,M是A1B1的中点,以C为坐标原点建立如图所示的空间直角坐标系C xyz,若⊥,则异面直线CM与A1B夹角的余弦值为________.
6.[2023·广东深圳高二测试]如图,已知AB,CD分别是圆柱上、下底面圆的直径,且AB⊥CD,若该圆柱的底面圆直径是其母线长的2倍,则异面直线AC与BD所成角的余弦值为________.
7.如图,在棱长为2的正方体ABCD A1B1C1D1中,E为BB1的中点.
(1)求异面直线AE与BC1所成的角的余弦值;
(2)求直线AB与平面AD1E所成的角的正弦值.
8.已知正三棱柱ABC A1B1C1,底面边长AB=2,AB1⊥BC1,O,O1分别是棱AC,A1C1的中点.建立如图所示的空间直角坐标系.
(1)求三棱柱的侧棱长;
(2)求异面直线AB1与BC所成角的余弦值.
9.[2023·辽宁凤城一中高二检测]如图,在四棱柱ABCD A1B1C1D1中,AA1⊥平面ABCD,底面ABCD满足AD∥BC,且AB=AD=AA1=2,BD=DC=2.
(1)求证:BD∥平面B1CD1;
(2)求直线AB与平面B1CD1所成角的正弦值.
核心素养升级练
1.在如图所示的四棱锥P ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,PA=PD=,AB=4,点M在侧棱PB上,且=λ,直线MC与平面BDP所成角的正弦值是,则实数λ的值是( )
A. B. C.或 D.或
2.[2023·安徽芜湖高二检测]如图,在正方体ABCD A1B1C1D1中,M为线段A1D的中点,N为线段CD1上的动点,则直线C1D与MN所成角的正弦值的最小值为________.
3.[2023·福建福州高二检测]已知在直三棱ABC A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,直线AB与平面DFE所成角的正弦值最大.
参考答案
必备知识基础练
1.答案:C
解析:因为θ∈(0,],所以cos θ=|cos 〈m,n〉|===,
sin θ==.故选C.
2.答案:C
解析:
由题意,取AC的中点O,建立如图所示的空间直角坐标系,则A(2,0,0),B(0,2,0),
B′(0,2,4),C′(-2,0,4),所以=(-2,2,4),=(-2,-2,4),
所以cos〈,〉===,所以AB′与BC′所成角的余弦值为.故选C.
3.答案:B
解析:
以D为坐标原点,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,
如图所示.设正方体的边长为1,则D(0,0,0),B(1,1,0),A1(1,0,1),C1(0,1,1),
=(-1,-1,0),=(1,0,1),=(0,1,1),
设平面A1C1D的法向量为n=(x,y,z),
则,令z=-1,则x=y=1,即n=(1,1,-1),
设BD与平面A1C1D所成角为θ,则sin θ===.故选B.
4.答案:B
解析:由题意,PA⊥平面ABCD,底面ABCD是边长为4的正方形,则有PA⊥AB,PA⊥AD,AB⊥AD,
而PA∩AB=A,故AD⊥平面PAB,
以A为原点,分别以AB、AD、AP所在直线为x轴、y轴、z轴建立空间直角坐标系,如图所示,
则A(0,0,0),D(0,4,0),C(4,4,0),P(0,0,6),E(0,2,3),
=(-4,-2,3),=(0,4,0).
设直线EC与平面PAB所成角为θ,又由题可知为平面PAB的一个法向量,
则sin θ=|cos 〈,〉|===.故选B.
5.答案:BCD
解析:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D xyz,
D1(0,0,2),B1(2,2,2),A1(2,0,2),D(0,0,0),易知=(2,2,0),=(0,1,0),
所以cos 〈,〉===,
所以异面直线B1D1与EF所成的角的大小为45°,故A正确,B错误;
由题意可知平面B1EF即为平面A1B1CD,设平面A1B1CD的法向量为n=(x,y,z),
则n·A1B1=n·DA1=0.又=(0,2,0),DA1=(2,0,2),
所以,令x=1,得n=(1,0,-1),
所以cos 〈,n〉==,
所以直线B1D1与平面A1B1CD所成的角为30°,即直线B1D1与平面B1EF所成的角的大小为30°,
故C,D错误.故选BCD.
6.答案:
解析:已知直线l的方向向量为d=(0,1,1),平面α的法向量为n=(-1,0,1),
设直线l与平面α所成角为θ,则θ∈[0,],∴sin θ===,∴θ=,
所以直线l与平面α所成角的大小为.
7.答案:
解析:平面xOz的一个法向量为n=(0,1,0),=(1,3,),所以cos 〈n,〉==.所以直线AB与平面xOz所成的角的正弦值为.
8.答案:
解析:依题意可知AC,BC,CC1两两相互垂直,由此建立如图所示空间直角坐标系,
设BC=AC=CC1=2,则A(2,0,0),F1(1,0,2),=(-1,0,2),B(0,2,0),D1(1,1,2),=(1,-1,2),设BD1与AF1所成角为α,则cos α===.
关键能力综合练
1.答案:A
解析:
取BD中点为O,连接AO,CO,所以AO⊥BD,CO⊥BD,又平面ABD⊥平面CBD且交线为BD,AO 平面ABD,所以AO⊥平面CBD,OC 平面CBD,则AO⊥CO.设正方形的对角线长度为2,
如图所示,建立空间直角坐标系,A(0,0,1),B(1,0,0),C(0,1,0),D(-1,0,0),所以=(1,0,-1),=(-1,-1,0),cos 〈,〉===-.所以异面直线AB与CD所成角的余弦值为.故选A.
2.答案:D
解析:
以OA,OC,OB所在直线为x轴,y轴,z轴建立空间直角坐标系(如图所示),则A(2,0,0),B(0,0,2),C(0,1,0),=(0,1,0),=(-2,0,2),=(-2,1,0),设平面ABC的一个法向量为m=(x,y,z),则,即,令x=1,则y=2,z=1,所以平面ABC的一个法向量为m=(1,2,1);
设直线OC与平面ABC所成角为θ,
则sin θ===,即直线OC与平面ABC所成角的正弦值为.故选D.
3.答案:A
解析:
如图,设上底面圆心为O1,下底面圆心为O,连接OO1,OC,OB,以O为原点,分别以OC,OB,OO1所在直线为x轴,y轴,z轴,建立空间直角坐标系,则C(2,0,0),A(0,4,0),B1(0,2,4),D1(4,0,4),则=(2,0,4),=(0,-2,4),cos 〈,〉===,又异面直线所成角的范围为(0,],故异面直线AB1与CD1所成角的余弦值为.故选A.
4.答案:ABC
解析:
如图所示,过点B在平面BCD内作BE⊥BC交CD于点E,过点B在平面ABC内作BF⊥BC交AC于点F,因为平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,BF⊥BC,BF 平面ABC,∴BF⊥平面BCD,同理可得BE⊥平面ABC,以点B为坐标原点,BE,BC,BF所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,设AB=BC=BD=2,则A(0,-1,),B(0,0,0),D(,-1,0),C(0,2,0).
对于A选项,=(,0,-),=(0,2,0),
则·=0,∴⊥,故直线AD与直线BC所成角的大小为90°,A对;
对于B选项,=(0,3,-),=(,-1,0),cos 〈,〉==-=-,所以直线AC与直线BD所成角的余弦值为,B对;
对于C选项,=(,0,-),平面BCD的一个法向量为m=(0,0,1),cos 〈,m〉==-=-,所以直线AD与平面BCD所成角的大小为45°,C对;
对于D选项,=(,-3,0),平面ABC的一个法向量为n=(1,0,0),cos 〈,n〉===,所以直线直线CD与平面ABC所成角的大小为30°,D错.故选ABC.
5.答案:
解析:设AA1=a,则B(0,4,0),A1(4,0,a),B1(0,4,a),C(0,0,0),M(2,2,a),可得=(-4,4,-a),=(0,4,a),∵⊥,则·=16-a2=0,得a=4,故=(2,2,4),=(-4,4,-4),∴cos 〈,〉===-,故异面直线CM与A1B夹角的余弦值为.
6.答案:
解析:
取CD的中点O,以O为原点,以CD所在直线为x轴,以底面内过点O且与CD垂直的直线为y轴,以过点O且与底面垂直的直线为z轴,建立如图所示的空间直角坐标系.设AB=2,则A(0,-1,1),B(0,1,1),C(-1,0,0),D(1,0,0),=(-1,1,-1),=(1,-1,-1),
所以|cos 〈,〉|===,所以异面直线AC与BD所成角的余弦值为.
7.解析:(1)以A为坐标原点,,,正方向为x,y,z轴,可建立如图所示空间直角坐标系,
则A(0,0,0),E(0,2,1),B(0,2,0),C1(2,2,2),D1(2,0,2),∴=(0,2,1),=(2,0,2),
∴|cos 〈,〉|===,
即异面直线AE与BC1所成角的余弦值为.
(2)由(1)知:=(0,2,0),=(0,2,1),AD1=(2,0,2),
设平面AD1E的法向量n=(x,y,z),
∴,
令y=1,解得z=-2,x=2,∴n=(2,1,-2),
∴|cos 〈,n〉|===,
即直线AB与平面AD1E所成角的正弦值为.
8.解析:(1)设侧棱长为b,则A(0,-1,0),B1(,0,b),B(,0,0),C1(0,1,b),C(0,1,0),
所以1=(,1,b),1=(-,1,b).
因为AB1⊥BC1,
所以1·1=-()2+12+b2=0,解得b=.
故三棱柱的侧棱长为.
(2)由(1)知1=(,1,),=(-,1,0).
因为|1|==,||==2,1·=-()2+1×1+×0=-2,
所以|cos 〈1,〉|===,
所以异面直线AB1与BC所成角的余弦值为.
9.解析:(1)证明:在四棱柱ABCD A1B1C1D1中,BB1∥DD1,BB1=DD1,
故四边形BB1D1D是平行四边形,
所以BD∥B1D1,
因为BD 平面B1CD1,B1D1 平面B1CD1,
所以BD∥平面B1CD1.
(2)因为AA1⊥平面ABCD,AB,AD 平面ABCD,
所以AA1⊥AB,AA1⊥AD,
因为AB=AD=2,BD=2,所以AB2+AD2=BD2,
所以AB⊥AD,
故AB,AD,AA1两两垂直,以A为坐标原点,分别以AB,AD,AA1为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(2,4,0),B1(2,0,2),D1(0,2,2),
所以=(2,0,0),B1C=(0,4,-2),B1D1=(-2,2,0).
设平面B1CD1的法向量为n=(x,y,z),
∴,即.令x=1,则y=1,z=2,
∴n=(1,1,2).
设直线AB与平面B1CD1所成角为θ,
∴sin θ=|cos 〈,n〉|===.
所以直线AB与平面B1CD1所成角的正弦值是.
核心素养升级练
1.答案:C
解析:
取AD的中点O,由PA=PD,得PO⊥AD,又PO 平面PAD,平面PAD⊥平面ABCD,可得OP⊥平面ABCD,设AC∩BD=E,由四边形ABCD是正方形,可知OE⊥AD.建立如图所示的空间直角坐标系,
则P(0,0,),C(2,4,0),D(2,0,0),B(-2,4,0),=(-2,4,-),=(4,-4,0),=(2,0,-).由=λ,得=+=λ+=λ(-2,4,-)+(0,0,)=(-2λ,4λ,-λ+),=(2+2λ,4-4λ,λ-),
设平面BDP的法向量为n=(x,y,z),则即令x=1,则y=1,z=,∴平面BDP的一个法向量为n=(1,1,),设直线MC与平面BDP所成的角为α,则sin α=|cos 〈n,〉|==
==,化简得44λ2-56λ+17=0,解得λ=,或λ=.故选C.
2.答案:
解析:
以D为原点建立如图所示的空间直角坐标系,设正方体棱长为2,
则M(1,0,1),C1(0,2,2),C(0,2,0),D(0,0,0),D1(0,0,2),则=(0,-2,-2),因为N为线段CD1上的动点,所以不妨设=λ (0≤λ≤1),则得N(0,-2λ+2,2λ),所以=(-1,-2λ+2,2λ-1),
则|cos 〈,〉|=
==.因为λ∈[0,1],所以8(λ-)2+∈[,6],进而∈[,],所以≤|cos 〈,〉|≤,故当|cos 〈,C1D〉|最大值为时,|sin 〈,〉|最小,且最小值为 =,所以直线C1D与直线MN所成角的正弦值的最小值为.
3.解析:(1)在直三棱柱ABC A1B1C1中,侧面AA1B1B为正方形,则AB⊥BB1,AB∥A1B1,而BF⊥A1B1,即有AB⊥BF,
又BF∩BB1=B,BF,BB1 平面BCC1B1,因此AB⊥平面BCC1B1,
而BC 平面BCC1B1,则AB⊥BC,显然BB1⊥BC,
以B为原点,BA、BC、BB1所在直线分别为x,y,z轴建立空间直角坐标系,如图,
则A(2,0,0),F(0,2,1),E(1,1,0),设D(a,0,2)(0≤a≤2),即=(0,2,1),=(1-a,1,-2),
有·=2-2=0,即有⊥,所以BF⊥DE.
(2)设平面DEF的法向量为n=(x,y,z),
由(1)知,=(-1,1,1),=(1-a,1,-2),
则,
令x=3,得n=(3,1+a,2-a),而=(2,0,0),
设直线AB与平面DFE所成的角为θ,
则sin θ=|cos 〈n,〉|=
==,
显然当a=时,(sin θ)max=,
所以当B1D=时,直线AB与平面DFE所成角的正弦值最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
用空间向量研究线线角、线面角
必备知识基础练
1.已知两条异面直线的方向向量分别是m=(-2,1,2),n=(3,-2,1),则这两条异面直线所成的角θ满足( )
A.sin θ=- B.sin θ= C.cos θ= D.cos θ=-
2.[2023·浙江杭州高二检测]在直三棱柱ABC A′B′C′中,侧棱长为4,底面是边长为4的正三角形,则异面直线AB′与BC′所成角的余弦值为( )
A. B. C. D.
3.在正方体ABCD A1B1C1D1中,BD与平面A1C1D所成角的正弦值是( )
A. B. C. D.1
4.已知在四棱锥P ABCD中,PA⊥平面ABCD,底面ABCD是边长为4的正方形,PA=6,E为棱PD的中点,则直线EC与平面PAB所成角的正弦值为( )
A. B. C. D.
5.(多选)如图,E,F分别是正方体ABCD A1B1C1D1中棱CD上的两点,且AB=2,EF=1,则下列命题中不正确的为( )
A.异面直线B1D1与EF所成的角的大小为45°
B.异面直线B1D1与EF所成的角的大小为30°
C.直线B1D1与平面B1EF所成的角的大小为45°
D.直线B1D1与平面B1EF所成的角的大小为60°
6.[2023·福建福州高二测试]若平面α的法向量n=(-1,0,1),直线l的方向向量为d=(0,1,1),则l与α所成角的大小为________.
7.在空间直角坐标系Oxyz中,已知A(1,-2,0),B(2,1,),则直线AB与平面xOz所成的角的正弦值为________.
8.[2023·天津蓟州高二检测]在直三棱柱ABC A1B1C1中,∠BCA=90°,D1,F1分别是A1B1,A1C1的中点,BC=AC=CC1,则BD1与AF1所成角的余弦值为________.
关键能力综合练
1.将正方形ABCD沿对角线BD折起,使得平面ABD⊥平面CBD,则异面直线AB与CD所成角的余弦值为( )
A. B. C.- D.-
2.如图,在四面体OABC中,OA,OB,OC两两垂直,已知OA=OB=2,OC=1,则直线OC与平面ABC所成角的正弦值为( )
A. B. C. D.
3.[2023·湖北广水高二检测]在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,它的高为4,AA1,BB1,CC1,DD1均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为2和4,对应的圆心角为90°,则图中异面直线AB1与CD1所成角的余弦值为( )
A. B. C. D.
4.[2023·福建龙岩高二检测](多选)如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°,则( )
A.直线AD与直线BC所成角的大小为90°
B.直线AC与直线BD所成角的余弦值为
C.直线AD与平面BCD所成角的大小为45°
D.直线CD与平面ABC所成角的大小为60°
5.[2023·辽宁抚顺高二检测]在直三棱柱ABC A1B1C1中,CA=4,CB=4,∠BCA=90°,M是A1B1的中点,以C为坐标原点建立如图所示的空间直角坐标系C xyz,若⊥,则异面直线CM与A1B夹角的余弦值为________.
6.[2023·广东深圳高二测试]如图,已知AB,CD分别是圆柱上、下底面圆的直径,且AB⊥CD,若该圆柱的底面圆直径是其母线长的2倍,则异面直线AC与BD所成角的余弦值为________.
7.如图,在棱长为2的正方体ABCD A1B1C1D1中,E为BB1的中点.
(1)求异面直线AE与BC1所成的角的余弦值;
(2)求直线AB与平面AD1E所成的角的正弦值.
8.已知正三棱柱ABC A1B1C1,底面边长AB=2,AB1⊥BC1,O,O1分别是棱AC,A1C1的中点.建立如图所示的空间直角坐标系.
(1)求三棱柱的侧棱长;
(2)求异面直线AB1与BC所成角的余弦值.
9.[2023·辽宁凤城一中高二检测]如图,在四棱柱ABCD A1B1C1D1中,AA1⊥平面ABCD,底面ABCD满足AD∥BC,且AB=AD=AA1=2,BD=DC=2.
(1)求证:BD∥平面B1CD1;
(2)求直线AB与平面B1CD1所成角的正弦值.
核心素养升级练
1.在如图所示的四棱锥P ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,PA=PD=,AB=4,点M在侧棱PB上,且=λ,直线MC与平面BDP所成角的正弦值是,则实数λ的值是( )
A. B. C.或 D.或
2.[2023·安徽芜湖高二检测]如图,在正方体ABCD A1B1C1D1中,M为线段A1D的中点,N为线段CD1上的动点,则直线C1D与MN所成角的正弦值的最小值为________.
3.[2023·福建福州高二检测]已知在直三棱ABC A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,直线AB与平面DFE所成角的正弦值最大.
参考答案
必备知识基础练
1.答案:C
解析:因为θ∈(0,],所以cos θ=|cos 〈m,n〉|===,
sin θ==.故选C.
2.答案:C
解析:
由题意,取AC的中点O,建立如图所示的空间直角坐标系,则A(2,0,0),B(0,2,0),
B′(0,2,4),C′(-2,0,4),所以=(-2,2,4),=(-2,-2,4),
所以cos〈,〉===,所以AB′与BC′所成角的余弦值为.故选C.
3.答案:B
解析:
以D为坐标原点,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,
如图所示.设正方体的边长为1,则D(0,0,0),B(1,1,0),A1(1,0,1),C1(0,1,1),
=(-1,-1,0),=(1,0,1),=(0,1,1),
设平面A1C1D的法向量为n=(x,y,z),
则,令z=-1,则x=y=1,即n=(1,1,-1),
设BD与平面A1C1D所成角为θ,则sin θ===.故选B.
4.答案:B
解析:由题意,PA⊥平面ABCD,底面ABCD是边长为4的正方形,则有PA⊥AB,PA⊥AD,AB⊥AD,
而PA∩AB=A,故AD⊥平面PAB,
以A为原点,分别以AB、AD、AP所在直线为x轴、y轴、z轴建立空间直角坐标系,如图所示,
则A(0,0,0),D(0,4,0),C(4,4,0),P(0,0,6),E(0,2,3),
=(-4,-2,3),=(0,4,0).
设直线EC与平面PAB所成角为θ,又由题可知为平面PAB的一个法向量,
则sin θ=|cos 〈,〉|===.故选B.
5.答案:BCD
解析:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系D xyz,
D1(0,0,2),B1(2,2,2),A1(2,0,2),D(0,0,0),易知=(2,2,0),=(0,1,0),
所以cos 〈,〉===,
所以异面直线B1D1与EF所成的角的大小为45°,故A正确,B错误;
由题意可知平面B1EF即为平面A1B1CD,设平面A1B1CD的法向量为n=(x,y,z),
则n·A1B1=n·DA1=0.又=(0,2,0),DA1=(2,0,2),
所以,令x=1,得n=(1,0,-1),
所以cos 〈,n〉==,
所以直线B1D1与平面A1B1CD所成的角为30°,即直线B1D1与平面B1EF所成的角的大小为30°,
故C,D错误.故选BCD.
6.答案:
解析:已知直线l的方向向量为d=(0,1,1),平面α的法向量为n=(-1,0,1),
设直线l与平面α所成角为θ,则θ∈[0,],∴sin θ===,∴θ=,
所以直线l与平面α所成角的大小为.
7.答案:
解析:平面xOz的一个法向量为n=(0,1,0),=(1,3,),所以cos 〈n,〉==.所以直线AB与平面xOz所成的角的正弦值为.
8.答案:
解析:依题意可知AC,BC,CC1两两相互垂直,由此建立如图所示空间直角坐标系,
设BC=AC=CC1=2,则A(2,0,0),F1(1,0,2),=(-1,0,2),B(0,2,0),D1(1,1,2),=(1,-1,2),设BD1与AF1所成角为α,则cos α===.
关键能力综合练
1.答案:A
解析:
取BD中点为O,连接AO,CO,所以AO⊥BD,CO⊥BD,又平面ABD⊥平面CBD且交线为BD,AO 平面ABD,所以AO⊥平面CBD,OC 平面CBD,则AO⊥CO.设正方形的对角线长度为2,
如图所示,建立空间直角坐标系,A(0,0,1),B(1,0,0),C(0,1,0),D(-1,0,0),所以=(1,0,-1),=(-1,-1,0),cos 〈,〉===-.所以异面直线AB与CD所成角的余弦值为.故选A.
2.答案:D
解析:
以OA,OC,OB所在直线为x轴,y轴,z轴建立空间直角坐标系(如图所示),则A(2,0,0),B(0,0,2),C(0,1,0),=(0,1,0),=(-2,0,2),=(-2,1,0),设平面ABC的一个法向量为m=(x,y,z),则,即,令x=1,则y=2,z=1,所以平面ABC的一个法向量为m=(1,2,1);
设直线OC与平面ABC所成角为θ,
则sin θ===,即直线OC与平面ABC所成角的正弦值为.故选D.
3.答案:A
解析:
如图,设上底面圆心为O1,下底面圆心为O,连接OO1,OC,OB,以O为原点,分别以OC,OB,OO1所在直线为x轴,y轴,z轴,建立空间直角坐标系,则C(2,0,0),A(0,4,0),B1(0,2,4),D1(4,0,4),则=(2,0,4),=(0,-2,4),cos 〈,〉===,又异面直线所成角的范围为(0,],故异面直线AB1与CD1所成角的余弦值为.故选A.
4.答案:ABC
解析:
如图所示,过点B在平面BCD内作BE⊥BC交CD于点E,过点B在平面ABC内作BF⊥BC交AC于点F,因为平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,BF⊥BC,BF 平面ABC,∴BF⊥平面BCD,同理可得BE⊥平面ABC,以点B为坐标原点,BE,BC,BF所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,设AB=BC=BD=2,则A(0,-1,),B(0,0,0),D(,-1,0),C(0,2,0).
对于A选项,=(,0,-),=(0,2,0),
则·=0,∴⊥,故直线AD与直线BC所成角的大小为90°,A对;
对于B选项,=(0,3,-),=(,-1,0),cos 〈,〉==-=-,所以直线AC与直线BD所成角的余弦值为,B对;
对于C选项,=(,0,-),平面BCD的一个法向量为m=(0,0,1),cos 〈,m〉==-=-,所以直线AD与平面BCD所成角的大小为45°,C对;
对于D选项,=(,-3,0),平面ABC的一个法向量为n=(1,0,0),cos 〈,n〉===,所以直线直线CD与平面ABC所成角的大小为30°,D错.故选ABC.
5.答案:
解析:设AA1=a,则B(0,4,0),A1(4,0,a),B1(0,4,a),C(0,0,0),M(2,2,a),可得=(-4,4,-a),=(0,4,a),∵⊥,则·=16-a2=0,得a=4,故=(2,2,4),=(-4,4,-4),∴cos 〈,〉===-,故异面直线CM与A1B夹角的余弦值为.
6.答案:
解析:
取CD的中点O,以O为原点,以CD所在直线为x轴,以底面内过点O且与CD垂直的直线为y轴,以过点O且与底面垂直的直线为z轴,建立如图所示的空间直角坐标系.设AB=2,则A(0,-1,1),B(0,1,1),C(-1,0,0),D(1,0,0),=(-1,1,-1),=(1,-1,-1),
所以|cos 〈,〉|===,所以异面直线AC与BD所成角的余弦值为.
7.解析:(1)以A为坐标原点,,,正方向为x,y,z轴,可建立如图所示空间直角坐标系,
则A(0,0,0),E(0,2,1),B(0,2,0),C1(2,2,2),D1(2,0,2),∴=(0,2,1),=(2,0,2),
∴|cos 〈,〉|===,
即异面直线AE与BC1所成角的余弦值为.
(2)由(1)知:=(0,2,0),=(0,2,1),AD1=(2,0,2),
设平面AD1E的法向量n=(x,y,z),
∴,
令y=1,解得z=-2,x=2,∴n=(2,1,-2),
∴|cos 〈,n〉|===,
即直线AB与平面AD1E所成角的正弦值为.
8.解析:(1)设侧棱长为b,则A(0,-1,0),B1(,0,b),B(,0,0),C1(0,1,b),C(0,1,0),
所以1=(,1,b),1=(-,1,b).
因为AB1⊥BC1,
所以1·1=-()2+12+b2=0,解得b=.
故三棱柱的侧棱长为.
(2)由(1)知1=(,1,),=(-,1,0).
因为|1|==,||==2,1·=-()2+1×1+×0=-2,
所以|cos 〈1,〉|===,
所以异面直线AB1与BC所成角的余弦值为.
9.解析:(1)证明:在四棱柱ABCD A1B1C1D1中,BB1∥DD1,BB1=DD1,
故四边形BB1D1D是平行四边形,
所以BD∥B1D1,
因为BD 平面B1CD1,B1D1 平面B1CD1,
所以BD∥平面B1CD1.
(2)因为AA1⊥平面ABCD,AB,AD 平面ABCD,
所以AA1⊥AB,AA1⊥AD,
因为AB=AD=2,BD=2,所以AB2+AD2=BD2,
所以AB⊥AD,
故AB,AD,AA1两两垂直,以A为坐标原点,分别以AB,AD,AA1为x轴,y轴,z轴建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(2,4,0),B1(2,0,2),D1(0,2,2),
所以=(2,0,0),B1C=(0,4,-2),B1D1=(-2,2,0).
设平面B1CD1的法向量为n=(x,y,z),
∴,即.令x=1,则y=1,z=2,
∴n=(1,1,2).
设直线AB与平面B1CD1所成角为θ,
∴sin θ=|cos 〈,n〉|===.
所以直线AB与平面B1CD1所成角的正弦值是.
核心素养升级练
1.答案:C
解析:
取AD的中点O,由PA=PD,得PO⊥AD,又PO 平面PAD,平面PAD⊥平面ABCD,可得OP⊥平面ABCD,设AC∩BD=E,由四边形ABCD是正方形,可知OE⊥AD.建立如图所示的空间直角坐标系,
则P(0,0,),C(2,4,0),D(2,0,0),B(-2,4,0),=(-2,4,-),=(4,-4,0),=(2,0,-).由=λ,得=+=λ+=λ(-2,4,-)+(0,0,)=(-2λ,4λ,-λ+),=(2+2λ,4-4λ,λ-),
设平面BDP的法向量为n=(x,y,z),则即令x=1,则y=1,z=,∴平面BDP的一个法向量为n=(1,1,),设直线MC与平面BDP所成的角为α,则sin α=|cos 〈n,〉|==
==,化简得44λ2-56λ+17=0,解得λ=,或λ=.故选C.
2.答案:
解析:
以D为原点建立如图所示的空间直角坐标系,设正方体棱长为2,
则M(1,0,1),C1(0,2,2),C(0,2,0),D(0,0,0),D1(0,0,2),则=(0,-2,-2),因为N为线段CD1上的动点,所以不妨设=λ (0≤λ≤1),则得N(0,-2λ+2,2λ),所以=(-1,-2λ+2,2λ-1),
则|cos 〈,〉|=
==.因为λ∈[0,1],所以8(λ-)2+∈[,6],进而∈[,],所以≤|cos 〈,〉|≤,故当|cos 〈,C1D〉|最大值为时,|sin 〈,〉|最小,且最小值为 =,所以直线C1D与直线MN所成角的正弦值的最小值为.
3.解析:(1)在直三棱柱ABC A1B1C1中,侧面AA1B1B为正方形,则AB⊥BB1,AB∥A1B1,而BF⊥A1B1,即有AB⊥BF,
又BF∩BB1=B,BF,BB1 平面BCC1B1,因此AB⊥平面BCC1B1,
而BC 平面BCC1B1,则AB⊥BC,显然BB1⊥BC,
以B为原点,BA、BC、BB1所在直线分别为x,y,z轴建立空间直角坐标系,如图,
则A(2,0,0),F(0,2,1),E(1,1,0),设D(a,0,2)(0≤a≤2),即=(0,2,1),=(1-a,1,-2),
有·=2-2=0,即有⊥,所以BF⊥DE.
(2)设平面DEF的法向量为n=(x,y,z),
由(1)知,=(-1,1,1),=(1-a,1,-2),
则,
令x=3,得n=(3,1+a,2-a),而=(2,0,0),
设直线AB与平面DFE所成的角为θ,
则sin θ=|cos 〈n,〉|=
==,
显然当a=时,(sin θ)max=,
所以当B1D=时,直线AB与平面DFE所成角的正弦值最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
