天津市蓟州区第一中学2023-2024学年高二下学期第一次月考检测数学试题(含答案)
文档属性
| 名称 | 天津市蓟州区第一中学2023-2024学年高二下学期第一次月考检测数学试题(含答案) | 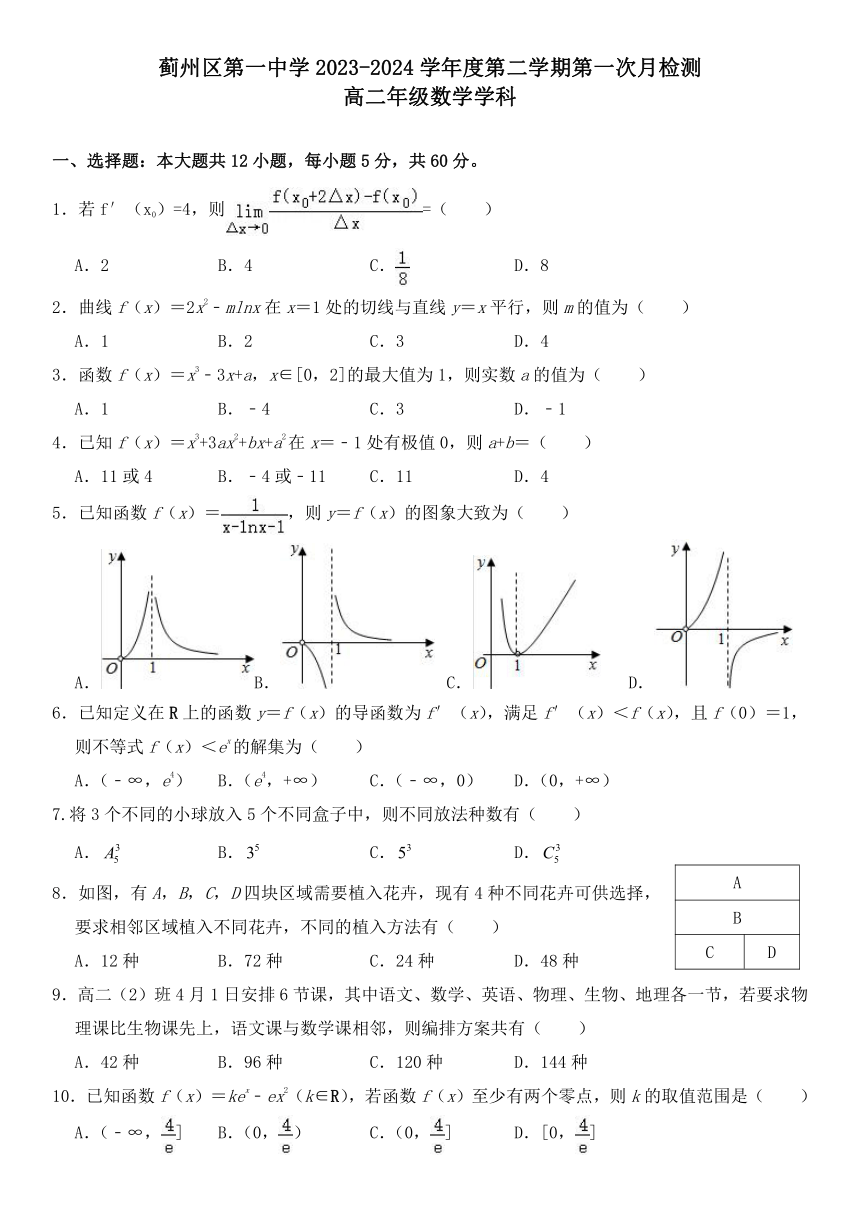 | |
| 格式 | docx | ||
| 文件大小 | 137.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 10:00:15 | ||
图片预览



文档简介
蓟州区第一中学2023-2024学年度第二学期第一次月检测
高二年级数学学科
一、选择题:本大题共12小题,每小题5分,共60分。
1.若f′(x0)=4,则=( )
A.2 B.4 C. D.8
2.曲线f(x)=2x2﹣mlnx在x=1处的切线与直线y=x平行,则m的值为( )
A.1 B.2 C.3 D.4
3.函数f(x)=x3﹣3x+a,x∈[0,2]的最大值为1,则实数a的值为( )
A.1 B.﹣4 C.3 D.﹣1
4.已知f(x)=x3+3ax2+bx+a2在x=﹣1处有极值0,则a+b=( )
A.11或4 B.﹣4或﹣11 C.11 D.4
5.已知函数f(x)=,则y=f(x)的图象大致为( )
A.B. C. D.
6.已知定义在R上的函数y=f(x)的导函数为f′(x),满足f′(x)<f(x),且f(0)=1,则不等式f(x)<ex的解集为( )
A.(﹣∞,e4) B.(e4,+∞) C.(﹣∞,0) D.(0,+∞)
7.将3个不同的小球放入5个不同盒子中,则不同放法种数有( )
A
B
C D
A. B. C. D.
8.如图,有A,B,C,D四块区域需要植入花卉,现有4种不同花卉可供选择,要求相邻区域植入不同花卉,不同的植入方法有( )
A.12种 B.72种 C.24种 D.48种
9.高二(2)班4月1日安排6节课,其中语文、数学、英语、物理、生物、地理各一节,若要求物理课比生物课先上,语文课与数学课相邻,则编排方案共有( )
A.42种 B.96种 C.120种 D.144种
10.已知函数f(x)=kex﹣ex2(k∈R),若函数f(x)至少有两个零点,则k的取值范围是( )
A.(﹣∞,] B.(0,) C.(0,] D.[0,]
11.已知函数f(x)=﹣x2+a,g(x)=x2ex,若对任意的x2∈[﹣1,1],存在,使得f(x1)=g(x2),则实数a的取值范围是( )
A.[e+1,4] B.[e,4] C. D.
12.已知函数f(x)=,g(x)=1+lnx,若f(m)=g(n),则m﹣n的最大值是( )
A.1 B.2 C.﹣ D.2ln2+3
二.填空题(共6小题,每题5分,共30分)
13.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有
种.(用数字填写答案)
14.将7个人分成三组,其中一组由3人组成,另外两组都由2人组成,则不同的分组方法种为 .(用数字填写答案)
15.已知函数f(x)=+2ax﹣lnx,若f(x)在区间上是增函数,则实数a的取值范围是 .
16.若函数f(x)=x3﹣3x2+2在区间(a﹣1,a+2)内存在极小值,则a的取值范围是 .
17.已知,g(x)=lnx+a-, x1∈[0,2], x2∈[1,3],使f(x1)≤g(x2)成立,则实数a的取值范围是 .
18.已知函数,x∈(,+∞),当x2>x1时,不等式恒成立,则实数a的取值范围为 .
三.解答题(共4小题,共60分)
19.(14分)已知函数f(x)=x3+ax2+bx的图象在点(0,f(0))处的切线斜率为﹣4,且x=﹣2时,y=f(x)有极值.
(1)求函数f(x)的解析式;(6分)
(2)求f(x)在[﹣3,1]上的最大值和最小值.(8分)
20.(15分)从包含甲、乙2人的7人中选4人参加4×100米接力赛,求在下列条件下,各有多少种不同的排法?(结果用数字作答,否则无分)
(1)甲、乙2人都被选中且必须跑中间两棒;
(2)甲、乙2人只有1人被选中且不能跑中间两棒;
(3)甲、乙2人都被选中且必须跑相邻两棒;
(4)甲、乙2人都被选中且不能相邻两棒;
(5)甲、乙2人都被选中且甲不能跑第一棒,乙不能跑第四棒.
21.(15分)已知函数f(x)=x﹣lnx,g(x)=x2﹣ax.
(Ⅰ)求函数f(x)的极值;;(4分)
(Ⅱ)令h(x)=g(x)﹣f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足,求实数a的取值范围;(5分)
(Ⅲ)若 x∈(0,1],使成立,求实数a的最大值.(6分)
22(16分).已知函数f(x)=x﹣lnx﹣2.
(1)求曲线y=f(x)在x=1处的切线方程;(3分)
(2)若,讨论函数g(x)的单调性.(5分)
(3)记函数,设x1,x2(x1<x2)是函数m(x)的两个极值点,若,且m(x1)﹣m(x2)≥k恒成立,求实数k的取值范围.(8分)
高二月考数学参考答案
1-5. DCDCA 6-10. DCBCC 11-12.BA
16 14. 105 15.
16.(0,3) 17. 18.
19.解:(1)由题意可得,f′(x)=3x2+2ax+b.
由解得
经检验得x=﹣2时,y=f(x)有极大值.
所以f(x)=x3+2x2﹣4x.
(2)由(1)知,f′(x)=3x2+4x﹣4=(x+2)(3x﹣2).
令f′(x)=0,得,
f′(x),f(x)的值随x的变化情况如下表:
x ﹣3 (﹣3,﹣2) ﹣2 (﹣2,) (,1) 1
f′(x) + 0 ﹣ 0 +
f(x) 3 ↑ 8 ↓ ↑
所以
(1)
(2)
(3)
(4)
(5)
21.解:(Ⅰ)因为f(x)=x﹣lnx,所以,
所以当x∈(0,1)时f′(x)<0,
当x∈(1,+∞)时f′(x)>0,
所以f(x)的极小值为f(1)=1,无极大值;
(Ⅱ)h(x)=x2﹣ax﹣x+lnx,
不妨设x2<x1,则x1﹣x2>0, 则由,可得h(x1)﹣h(x2)<2x1﹣2x2,
变形得h(x1)﹣2x1<h(x2)﹣2x2恒成立,
令F(x)=h(x)﹣2x=x2﹣(a+3)x+lnx,
则F(x)=x2﹣(a+3)x+lnx在(0,+∞)上单调递增,
故恒成立,
∴在(0,+∞)恒成立,
法一:∵,当且仅当时取“=”,
即实数a的取值范围是(﹣∞,2﹣3];
法二:
所以
所以
即实数a的取值范围是(﹣∞,2﹣3];
(Ⅲ)∵,∴a(x+1) 2x2﹣xlnx,
∵x∈(0,1],∴x+1∈(1,2],
∴ x∈(0,1]使得成立,
令,则,
令y=2x2+3x﹣lnx﹣1,
则由,可得或x=﹣1(舍),
当时,y′<0,则y=2x2+3x﹣lnx﹣1在上单调递减,
当时,y>0,则y=2x2+3x﹣lnx﹣1在上单调递增,
∴,∴t′(x)>0在x∈(0,1]上恒成立,
∴t(x)在(0,1]上单调递增,则a t(1),即a 1,
∴实数a的最大值为1.
(1) 因为,∴切线斜率为f'(1)=0,
又f(1)=﹣1,切点为(1,﹣1),所以切线方程为y=﹣1;
(2)∵= (x>0)
∴当a=0时, 增区间为(0,1);减区间为(1,+∞);
①当,即时, ,增区间为(0,+∞).
②当,即时, 令g'(x)>0得,0<x<1或;令g'(x)<0得,.
所以,增区间为;减区间为;
③当,即时,令g'(x)>0得,或x>1; 令g'(x)<0得,.
所以,增区间为;减区间为;
综上,当a=0时,增区间为(0,1);减区间为(1,+∞);
当时,增区间为(0,+∞);
当时,增区间为;减区间为;
当时,增区间为;减区间为.
(3)函数,x∈(0,+∞),
所以, 由g'(x)=0,得x2﹣(b+1)x+1=0,
依题意方程x2﹣(b+1)x+1=0有两不相等的正实根x1、x2,
∴x1+x2=b+1, x1x2=1,
∴, 又, 则,解得,
∴,
构造函数,
,
∴F(x)在上单调递减;
当x=3时,, 所以.
高二年级数学学科
一、选择题:本大题共12小题,每小题5分,共60分。
1.若f′(x0)=4,则=( )
A.2 B.4 C. D.8
2.曲线f(x)=2x2﹣mlnx在x=1处的切线与直线y=x平行,则m的值为( )
A.1 B.2 C.3 D.4
3.函数f(x)=x3﹣3x+a,x∈[0,2]的最大值为1,则实数a的值为( )
A.1 B.﹣4 C.3 D.﹣1
4.已知f(x)=x3+3ax2+bx+a2在x=﹣1处有极值0,则a+b=( )
A.11或4 B.﹣4或﹣11 C.11 D.4
5.已知函数f(x)=,则y=f(x)的图象大致为( )
A.B. C. D.
6.已知定义在R上的函数y=f(x)的导函数为f′(x),满足f′(x)<f(x),且f(0)=1,则不等式f(x)<ex的解集为( )
A.(﹣∞,e4) B.(e4,+∞) C.(﹣∞,0) D.(0,+∞)
7.将3个不同的小球放入5个不同盒子中,则不同放法种数有( )
A
B
C D
A. B. C. D.
8.如图,有A,B,C,D四块区域需要植入花卉,现有4种不同花卉可供选择,要求相邻区域植入不同花卉,不同的植入方法有( )
A.12种 B.72种 C.24种 D.48种
9.高二(2)班4月1日安排6节课,其中语文、数学、英语、物理、生物、地理各一节,若要求物理课比生物课先上,语文课与数学课相邻,则编排方案共有( )
A.42种 B.96种 C.120种 D.144种
10.已知函数f(x)=kex﹣ex2(k∈R),若函数f(x)至少有两个零点,则k的取值范围是( )
A.(﹣∞,] B.(0,) C.(0,] D.[0,]
11.已知函数f(x)=﹣x2+a,g(x)=x2ex,若对任意的x2∈[﹣1,1],存在,使得f(x1)=g(x2),则实数a的取值范围是( )
A.[e+1,4] B.[e,4] C. D.
12.已知函数f(x)=,g(x)=1+lnx,若f(m)=g(n),则m﹣n的最大值是( )
A.1 B.2 C.﹣ D.2ln2+3
二.填空题(共6小题,每题5分,共30分)
13.从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有
种.(用数字填写答案)
14.将7个人分成三组,其中一组由3人组成,另外两组都由2人组成,则不同的分组方法种为 .(用数字填写答案)
15.已知函数f(x)=+2ax﹣lnx,若f(x)在区间上是增函数,则实数a的取值范围是 .
16.若函数f(x)=x3﹣3x2+2在区间(a﹣1,a+2)内存在极小值,则a的取值范围是 .
17.已知,g(x)=lnx+a-, x1∈[0,2], x2∈[1,3],使f(x1)≤g(x2)成立,则实数a的取值范围是 .
18.已知函数,x∈(,+∞),当x2>x1时,不等式恒成立,则实数a的取值范围为 .
三.解答题(共4小题,共60分)
19.(14分)已知函数f(x)=x3+ax2+bx的图象在点(0,f(0))处的切线斜率为﹣4,且x=﹣2时,y=f(x)有极值.
(1)求函数f(x)的解析式;(6分)
(2)求f(x)在[﹣3,1]上的最大值和最小值.(8分)
20.(15分)从包含甲、乙2人的7人中选4人参加4×100米接力赛,求在下列条件下,各有多少种不同的排法?(结果用数字作答,否则无分)
(1)甲、乙2人都被选中且必须跑中间两棒;
(2)甲、乙2人只有1人被选中且不能跑中间两棒;
(3)甲、乙2人都被选中且必须跑相邻两棒;
(4)甲、乙2人都被选中且不能相邻两棒;
(5)甲、乙2人都被选中且甲不能跑第一棒,乙不能跑第四棒.
21.(15分)已知函数f(x)=x﹣lnx,g(x)=x2﹣ax.
(Ⅰ)求函数f(x)的极值;;(4分)
(Ⅱ)令h(x)=g(x)﹣f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足,求实数a的取值范围;(5分)
(Ⅲ)若 x∈(0,1],使成立,求实数a的最大值.(6分)
22(16分).已知函数f(x)=x﹣lnx﹣2.
(1)求曲线y=f(x)在x=1处的切线方程;(3分)
(2)若,讨论函数g(x)的单调性.(5分)
(3)记函数,设x1,x2(x1<x2)是函数m(x)的两个极值点,若,且m(x1)﹣m(x2)≥k恒成立,求实数k的取值范围.(8分)
高二月考数学参考答案
1-5. DCDCA 6-10. DCBCC 11-12.BA
16 14. 105 15.
16.(0,3) 17. 18.
19.解:(1)由题意可得,f′(x)=3x2+2ax+b.
由解得
经检验得x=﹣2时,y=f(x)有极大值.
所以f(x)=x3+2x2﹣4x.
(2)由(1)知,f′(x)=3x2+4x﹣4=(x+2)(3x﹣2).
令f′(x)=0,得,
f′(x),f(x)的值随x的变化情况如下表:
x ﹣3 (﹣3,﹣2) ﹣2 (﹣2,) (,1) 1
f′(x) + 0 ﹣ 0 +
f(x) 3 ↑ 8 ↓ ↑
所以
(1)
(2)
(3)
(4)
(5)
21.解:(Ⅰ)因为f(x)=x﹣lnx,所以,
所以当x∈(0,1)时f′(x)<0,
当x∈(1,+∞)时f′(x)>0,
所以f(x)的极小值为f(1)=1,无极大值;
(Ⅱ)h(x)=x2﹣ax﹣x+lnx,
不妨设x2<x1,则x1﹣x2>0, 则由,可得h(x1)﹣h(x2)<2x1﹣2x2,
变形得h(x1)﹣2x1<h(x2)﹣2x2恒成立,
令F(x)=h(x)﹣2x=x2﹣(a+3)x+lnx,
则F(x)=x2﹣(a+3)x+lnx在(0,+∞)上单调递增,
故恒成立,
∴在(0,+∞)恒成立,
法一:∵,当且仅当时取“=”,
即实数a的取值范围是(﹣∞,2﹣3];
法二:
所以
所以
即实数a的取值范围是(﹣∞,2﹣3];
(Ⅲ)∵,∴a(x+1) 2x2﹣xlnx,
∵x∈(0,1],∴x+1∈(1,2],
∴ x∈(0,1]使得成立,
令,则,
令y=2x2+3x﹣lnx﹣1,
则由,可得或x=﹣1(舍),
当时,y′<0,则y=2x2+3x﹣lnx﹣1在上单调递减,
当时,y>0,则y=2x2+3x﹣lnx﹣1在上单调递增,
∴,∴t′(x)>0在x∈(0,1]上恒成立,
∴t(x)在(0,1]上单调递增,则a t(1),即a 1,
∴实数a的最大值为1.
(1) 因为,∴切线斜率为f'(1)=0,
又f(1)=﹣1,切点为(1,﹣1),所以切线方程为y=﹣1;
(2)∵= (x>0)
∴当a=0时, 增区间为(0,1);减区间为(1,+∞);
①当,即时, ,增区间为(0,+∞).
②当,即时, 令g'(x)>0得,0<x<1或;令g'(x)<0得,.
所以,增区间为;减区间为;
③当,即时,令g'(x)>0得,或x>1; 令g'(x)<0得,.
所以,增区间为;减区间为;
综上,当a=0时,增区间为(0,1);减区间为(1,+∞);
当时,增区间为(0,+∞);
当时,增区间为;减区间为;
当时,增区间为;减区间为.
(3)函数,x∈(0,+∞),
所以, 由g'(x)=0,得x2﹣(b+1)x+1=0,
依题意方程x2﹣(b+1)x+1=0有两不相等的正实根x1、x2,
∴x1+x2=b+1, x1x2=1,
∴, 又, 则,解得,
∴,
构造函数,
,
∴F(x)在上单调递减;
当x=3时,, 所以.
同课章节目录
