湘教版初中数学导学案八年级上册第3章 实数
文档属性
| 名称 | 湘教版初中数学导学案八年级上册第3章 实数 |  | |
| 格式 | zip | ||
| 文件大小 | 439.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-05 09:55:17 | ||
图片预览




文档简介
第3章 实 数
3.1 平方根(1)
1.理解平方根、算术平方根的概念,知道开平方与平方互为逆运算.
2.会求非负数的平方根、算术平方根.
一、 新知探究
阅读教材第105~107页的内容,自主探究,回答下列问题:
1.填写平方根与算术平方根的对照表:
名称 平方根 算术平方根
定义 若r2=a,则 是 的一个平方根 正数a的 平方根,叫作a的算术平方根
表示方法 (a为被开方数) (a为被开方数)
a>0 有 个,它们互为 有 个,是
a=0 结果为 结果为
a<0 (存在/不存在) (存在/不存在)
2.试着写出开平方的定义,开平方与平方有什么关系
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.下列各数有平方根的是 .
①81; ②; ③1.69; ④2; ⑤0; ⑥-16.
2.下列说法中正确的是 ( )
A. -1的平方根是-1
B.的平方根是±2
C. 2是4的一个平方根
D. 0.9的平方根是±0.3
3.(1)求下列各数的平方根:25,,0.01.
学法指导:仿照教材第107页例1、例2完成,注意书写格式.
(2)求下列各数的算术平方根:
121,,1.96,1.
学法指导:当被开方数是带分数时,可先把带分数化成假分数.
4.计算:= ,-= ,
±= .
5. 36的平方根是 ,算术平方根是 .
14的平方根是 ,算术平方根是 .
(-4)2的平方根是 ,算术平方根是 .
的平方根是 ,算术平方根是 .
的平方根是 ,算术平方根是 .
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.若x2=16,求5-x的值.
2.一个正数的平方根为x+3与2x-6,求这个正数.
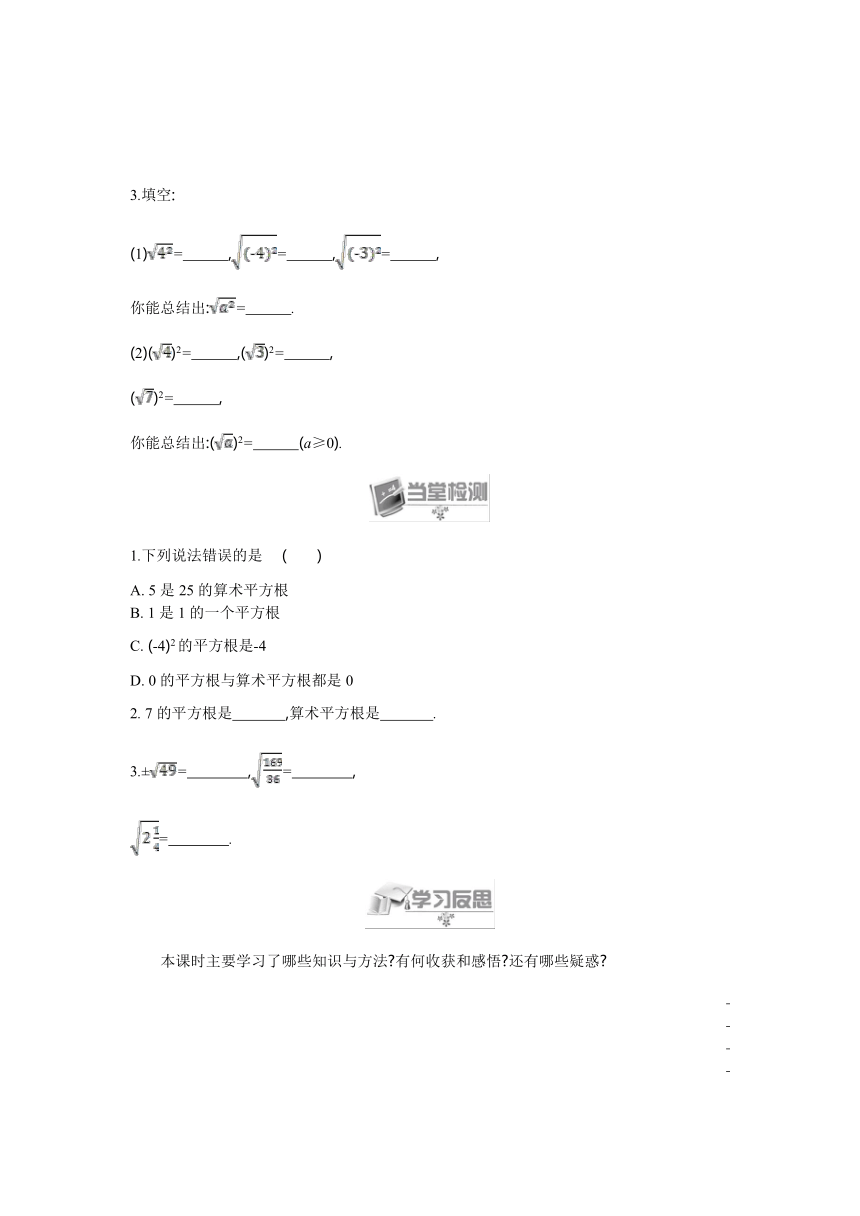
3.填空:
(1)= ,= ,= ,
你能总结出:= .
(2)()2= ,()2= ,
()2= ,
你能总结出:()2= (a≥0).
1.下列说法错误的是 ( )
A. 5是25的算术平方根
B. 1是1的一个平方根
C. (-4)2的平方根是-4
D. 0的平方根与算术平方根都是0
2. 7的平方根是 ,算术平方根是 .
3.±= ,= ,
= .
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
看谁记得最牢
12=1, 112=121, 13=1,
22=4, 122=144, 23=8,
32=9, 132=169, 33=27,
42=16, 142=196, 43=64,
52=25, 152=225, 53=125,
62=36, 162=256, 63=216,
72=49, 172=289, 73=343,
82=64, 182=324, 83=512,
92=81, 192=361, 93=729,
102=100, 202=400, 103=1000.
1.下列说法正确的是 ( )
A.如果一个数有平方根,那么这个数的平方根一定有两个
B.任何一个非负数的平方根都是非负数
C. -a2一定没有平方根
D. a2+1一定有平方根
2. 625的算术平方根是 ,平方根是 .
11的算术平方根是 ,平方根是 .
的算术平方根是 ,平方根是 .
3.计算:
±= ,-= ,
= ,= ,
()2= ,= .
4.求下列各式中的x.
(1)x2=49; (2)x2-144=0.
5.已知2x-1的平方根为±3,3x+y-1的平方根为±4,求x+2y的平方根.
3.1 平方根(2)
1.理解无理数的概念以及常见的几种表现形式,能区分有理数和无理数.
2.会用计算器求平方根,记住常见平方根的估值.
一、 新知探究
阅读教材第108~110页的内容,自主探究,回答下列问题:
1.什么数叫作无理数
2.无理数有哪些表现形式 试举例说明.
3.试着写出用计算器求平方根的按键步骤.
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.下列各数是无理数的是 .
-,,-,-3.14,0.010 010 001…,0.,0,
2.判断下列语句是否正确,并说明原因.
(1)3.787 887 888 788 88是无理数;
(2)无理数可以分为正无理数、负无理数;
(3)无限小数不能化成分数;
(4)无理数是无限小数;
(5)无限小数是无理数;
(6)带有根号的数都是无理数.
3.面积为3的正方形的边长 有理数;
面积为4的正方形的边长 有理数.
(填“是”或“不是”)
4.用计算器求下列各式的值.(精确到0.001)
≈ ,≈ ,
≈ ,≈ .
5.最接近的整数是 ,-最接近的整数是 ,的整数部分是 .
温馨提示:这些都是常用的平方根,记住它们的估计值很有用哦.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.比较下列四个数的大小:5,,4,.
2.已知3a+1的平方根是±4,2a+b-1的平方根是±3,c是的整数部分,求a+2b+c的平方根.
1.下列各数是无理数的是 ( )
A. 0.1 B. C. 0 D.
2.最接近的整数是 ,的整数部分是 .
3.比较大小: 8.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
胡同捉鸡与求算术平方根
不知谁家的鸡跑到胡同里来了.忽然,从一家 ( http: / / www.21cnjy.com )院子里跑出来一个小男孩,他想捉住这只鸡.只见鸡在前面,一会儿快跑,一会儿慢走,小男孩一个劲地在后面追,累得满头大汗,也没有捉住这只鸡.这时候,从胡同的另一头走来一个小女孩,两个人一人把住一头,一步一步地逼近鸡.当两个小孩碰面的时候,鸡无处可逃,终于被捉住了.我们用试凑法求的过程就类似胡同捉鸡.
首先拿1作答案试一试,因为1× HYPERLINK "http://www.21cnjy.com" 1=1,比要小,看来用1作2的算术平方根偏小了.用2试一试,因为2×2=4,比2要大.看来用2作为2的算术平方根偏大了.
经过了两次试验,我们知道的值在1和2之间.
用1.5去试,因为1.5×1.5=2.25 ( http: / / www.21cnjy.com ),也偏大,但是我们看到这个值比1和4都更接近2.再用1.4去试,因为1.4×1.4=1.96,1.96与2仅差0.04,更接近2.必然在1.4和1.5之间,而且靠近1.4.再试1.41,因为1.41×1.41=1.988 1,这个值比2小.再试1.42,因为1.42×1.42=2.016 4,比2大.所以的值在1.41和1.42之间.
这个试算过程可以一直持续下去,一直算到所需要的小数位.
这种“寻找”的想法非常重要,它是用已知去探求、捕捉未知的一种基本方法,在数学中经常会用到.如果把数轴当作一条胡同,把看作跑进胡同里的鸡,用试凑法求的值类似胡同里捉鸡,用两串数把夹在中间,不断缩小两串数的差:
1<<2;1.4<<1.5;1.41<<1.42;1.414<<1.415;1.414 2<<1.414 3;…
需要精确到多少位,就可以精确到多少 ( http: / / www.21cnjy.com )位.用试凑法求平方根,必须从一大一小两边来逼近.不能像小男孩捉鸡那样,一个人只从一面去捉,这样就难以把鸡捉住.
1.下列说法正确的是 ( )
A.带根号的数叫无理数
B.无理数一定是带根号的数
C.无限小数是无理数
D.无理数是无限小数
2.在,,0.020 202…,,2π,中,无理数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
3.用计算器求下列各式的值.
(1)= .(精确到0.001)
(2)25.8的平方根是 .(精确到0.000 1)
4.填空:
(1)若=2,则y= ;
(2)的整数部分是 ,最接近的整数是 .
5.例题:∵<<,即2<<3,∴的整数部分为2,小数部分为(-2).请你观察上述例题后试解下面的问题:
(1)的整数部分是 ,小数部分是 ;
(2)如果的小数部分为a,的小数部分为b,求a+b-5的值.
3.2 立方根
1.理解立方根的意义,会表示立方根.
2.能用立方运算求立方根.
3.会用计算器求立方根.
一、 新知探究
阅读教材第112、113页的内容,自主探究,回答下列问题:
1.请类比平方根的定义及性质,试着写出立方根的定义及性质:
名称 平方根 立方根
定义 若r2=a,则 是 的一个平方根 若b3=a,则 是 的一个立方根
表示方法 (a为被开方数) (a为被开方数)
a>0 有 个值,是 有 个值,是
a=0 有 个值,是 有 个值,是
a<0 (存在/不存在) 有 个值,是
2.试着写出开立方的定义,开立方与立方有什么关系
3.试着写出用计算器求立方根的按键步骤.
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.根据开立方与立方的关系,求下列各数的立方根:
(1)8; (2)0.001; (3)0; (4)-.
学法指导:仿照教材第113页例1完成,注意书写格式.
2.判断下列说法是否正确,并说明理由.
(1)的立方根是±;
(2)-64没有立方根;
(3)8的立方根是2;
(4)互为相反数的两个数的立方根也互为相反数;
(5)互为相反数的两个数的立方也互为相反数.
3.计算:
(1)= ;
(2)= ;
(3)-= ;
(4)-= .
4.用计算器求下列各数的近似值.(精确到0.001)
≈ ;≈ ;≈ .
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.计算:
(1)= ;(2)= .
2.(1)由于= ,因此()3= ;
()3= ,()3= ;
你能总结出:()3= .
(2)由于53= ,因此= ;
= ,= ;
你能总结出:= .
3.求下列各数的值.
(1)8x3+27=0;
(2)(x-1)3-0.343=0.
1. 125的立方根是 ,0.125的立方根是 .
2.计算:= ,= .
3.计算:= ,()3= .
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
立方根近似值的求法
当立方根是一位整数时,很容易求出这 ( http: / / www.21cnjy.com )个立方根;但当立方根是两位或两位以上的整数时,也能容易地求出吗 例如求140 608的立方根,怎样求容易呢
下面就介绍它的巧妙求法.
先用前三位数140来确定立方根的十位数.因为 ( http: / / www.21cnjy.com )53<140<63,所以十位数是5,而不是6.再用最后一位数8来确定立方根的个位数.因为23=8,所以个位数是2.就是说,140 608的立方根是52.确定立方根的个位数时要注意下面规律:我们知道:13=1,43=64,53=125,63=216,93=729,就是说当被开方数的末位数是1,4,5,6,9时,立方根的个位数就等于它本身(1,4,5,6,9).
因为23=8,83=512 ( http: / / www.21cnjy.com ),就是说当被开方数的末位数是8和2时,立方根的个位数就分别是2和8,叫作2与8互换原则;同样还有3与7互换原则(被开方数的末位数分别是3和7,立方根的个位数就分别是7和3).
一般地,如果10321 952,50 653,79 507,287 496,970 299
1.下列叙述中,错误的有 ( )
①正数的平方根是正数;
②正数的立方根不一定是正数;
③任意一个正数的立方根都不等于它本身;
④ 0的立方根是0;
⑤-3是27的负的立方根.
A. 1个 B. 2个 C. 3个 D. 4个
2. 2的立方根为 ,-2是 的立方根.-125的立方根为 ,的立方根为 ,的立方根为 .
3.用计算器求下列各数的近似值.(精确到0.01)
≈ ,≈ ,
≈ ,≈ .
4.= ,-= ,
= ,(-)3= ,
= .
5. (1)=3,那么x= .
(2)若b是的小数部分,则-b= .
(3)x是(-)2的平方根,y是64的立方根,则x+y= .
3.3 实数(1)
1.知道实数的概念,掌握实数的分类.
2.理解实数和数轴上的点一一对应的关系.
3.会求实数的相反数与绝对值.
一、 新知探究
阅读教材第116~118页的内容,自主探究,回答下列问题:
1.什么叫作实数,你能对实数按定义进行分类吗 还可以按正负分类吗
2.你知道数轴上的点与实数有什么关系吗
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.把下列各数填在相应的括号里.
0,,-,π,,0.,,,1.313 131,0.101 001 000…
整数有( )
有理数有( )
无理数有( )
负实数有( )
2.下列说法正确的是 ( )
A.实数可以划分为正实数和负实数两大类
B.有理数的相反数是无理数
C.数轴上的每一个点都表示一个有理数
D.每个实数a有且只有一个立方根
3.求出下列各数的相反数和绝对值.
2π - 2- 3.141 5-π
相反数
绝对值
4.若=π,则x= ;若a与互为相反数,则a= ;在数轴上表示-的点到原点的距离为 .
5.如图所示,在数轴上点A,B对应的实数分别为a,b,则有 ( )
A. a+b>0 B. a-b>0
C. ab>0 D. >0
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.下列各组数中互为相反数的是 ( )
A. -2与 B. -2与
C. 2与 D. 与
2.实数a,b在数轴上的位置如图所示,化简:+-.
1.实数可分为 ( )
A.正实数和负实数
B.有理数和无理数
C.小数和分数
D.整数和无理数
2.-的相反数是 ,绝对值是 ;π-3.14的相反数是 ,绝对值是 .
3.实数a,b在数轴上的位置如图所示,则a与b的大小关系是 ( )
A. a>b B. a=b
C. a0
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
“精确值”毫无精确意义
十六世纪,欧洲莱顿地区的 ( http: / / www.21cnjy.com )声道尔夫将π计算到小数点后35位,并且在遗嘱上写明,要后人把这个π的数值刻在他的墓碑上,这就是著名的“π墓志铭”,墓碑上刻下的值是:
3.141 592 653 585 793 238 462 643 383 279 502 88.
随着现代科学技术的发展,借助计算机计算 ( http: / / www.21cnjy.com )π的值就容易得多了.1949年算到2 035位,1958年超过了1万位,1973年超过了300万位,1993年日本的科学家借助先进的计算机,已把π算到了800万位以后.
1979年10月日本人左奇英哲把π的值 ( http: / / www.21cnjy.com )背诵到小数点后两万位,被人们称为“世界上记忆力最强的人”.古代和现代数学家不断有人想要打破π值的纪录,实际上并无多大意义.原苏联数学家格拉维夫斯基证明了π的值即使算到100位都完全没有必要.他算出:假设有一个球体,它的半径等于地球到天狼星的距离R=1.32×1012公里,在这个球中装满了微生物,假定球的每1立方毫米中有1010个微生物,然后把所有微生物排列在一条线上,使每两个相邻微生物的间距等于地球到天狼星的距离,那么,拿这个幻想长度来作为圆的直径,取π的精确值到小数点后100位,可以算出这个巨圆的周长精确到0.000 000 01毫米以下.法国天文学家阿拉哥曾说过“无休止地追求π的精确值,没有丝毫精确意义”.
1.把下列各数填在相应的括号里.
,0.,,,3.14,3.333,0,-3,-2π,0.080 080 008…
整数有( )
有理数有( )
无理数有( )
负实数有( )
2.在实数中 ( )
A.实数的绝对值都是正数
B.有绝对值最大的数,也有绝对值最小的数
C.没有绝对值最大的数,但有绝对值最小的数
D.没有绝对值最大的数,也没有绝对值最小的数
3.下列实数中,无理数是 ( )
A. 5.010 101… B. 2π
C. D.
4. -的相反数是 ,绝对值是 .
π-3的相反数是 ,绝对值是 .
-3的相反数是 ,绝对值是 .
5.实数a,b在数轴上的位置如图所示,则与的大小关系是 .
3.3 实数(2)
1.了解有理数的运算法则、运算律等在实数范围内仍然成立.
2.会比较实数的大小.
3.会计算在实数范围内的简单计算题.
一、 新知探究
阅读教材第118~120页的内容,自主探究,回答下列问题:
1.有理数的运算律在实数范围内仍然成立的有哪些
2.怎么比较两个实数的大小
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.计算:
(1)(-2)+2;
(2)5+2-;
(3)5-3+;
(4)+-.
2.比较大小.
(1)7与4; (2)-3与-2.
3.用计算器计算.(精确到0.01)
(1)π; (2)÷.
4.已知m<-4三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.解下列方程:
(1)3x-=0; (2)-=.
2.比较与的大小.
学法指导:
(1)平方法:把两个数分别平方去掉根号,再比较大小;
(2)估值法:把无理数化成小数形式的估计值,再比较.
3.如图,A表示1,B表示,C到A的距离与B到A的距离相等,求C表示的数.
学法指导:你可以有多少种方法求C表示的数
1.用“>”、“<”、“=”填空.
(1)5 ; (2)-1 0.4.
2.计算:
(1)2-+3;
(2)()2-4×+(-2)3.
3.用计算器计算.(精确到0.01)
(1)×; (2)+.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
实数的性质
实数可实现的基本运算有加、减、乘、 ( http: / / www.21cnjy.com )除、乘方等,对非负数(即正数和0)还可以进行开方运算.实数加、减、乘、除(除数不为零)、平方后结果还是实数.任何实数都可以开奇次方,结果仍是实数,只有非负实数,才能开偶次方其结果还是实数.
四则运算封闭性:实数集R对加、减、乘、除(除数不为零)四则运算具有封闭性,即任意两个实数的和、差、积、商(除数不为零)仍然是实数.
实数集有序性:实数集是有序的,即任意两个实数a、b必定满足下列三个关系之一:ab.
实数的传递性:实数大小具有传递性,即若a>b,b>c,则有a>c.
实数的阿基米德性:实数具有阿基米德(Archimedes)性,即对任何a,b∈R,若b>a>0,则存在正整数n,使得na>b.
实数的稠密性:实数集R具有稠密性,即两个不相等的实数之间必有另一个实数,既有有理数,也有无理数.
实数唯一性:如果在一条直线(通常为水平直 ( http: / / www.21cnjy.com )线)上确定O作为原点,指定一个方向为正方向(通常把指向右的方向规定为正方向),并规定一个单位长度,则称此直线为数轴.任一实数都对应与数轴上的唯一一个点;反之,数轴上的每一个点也都唯一的表示一个实数.于是,实数集R与数轴上的点有着一一对应的关系.
1.用“>”、“<”、“=”填空.
(1) 3; (2)- -;
(3)3 2; (4) 1.6.
2.比较下列各组数的大小.
(1)-与-2.5;
(2)与.
3.计算:
(1)(-2)+3;
(2)+.
4.用计算器计算.(精确到0.001)
(1)3-π; (2)÷-3.
5.化简:++.
3.1 平方根(1)
1.理解平方根、算术平方根的概念,知道开平方与平方互为逆运算.
2.会求非负数的平方根、算术平方根.
一、 新知探究
阅读教材第105~107页的内容,自主探究,回答下列问题:
1.填写平方根与算术平方根的对照表:
名称 平方根 算术平方根
定义 若r2=a,则 是 的一个平方根 正数a的 平方根,叫作a的算术平方根
表示方法 (a为被开方数) (a为被开方数)
a>0 有 个,它们互为 有 个,是
a=0 结果为 结果为
a<0 (存在/不存在) (存在/不存在)
2.试着写出开平方的定义,开平方与平方有什么关系
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.下列各数有平方根的是 .
①81; ②; ③1.69; ④2; ⑤0; ⑥-16.
2.下列说法中正确的是 ( )
A. -1的平方根是-1
B.的平方根是±2
C. 2是4的一个平方根
D. 0.9的平方根是±0.3
3.(1)求下列各数的平方根:25,,0.01.
学法指导:仿照教材第107页例1、例2完成,注意书写格式.
(2)求下列各数的算术平方根:
121,,1.96,1.
学法指导:当被开方数是带分数时,可先把带分数化成假分数.
4.计算:= ,-= ,
±= .
5. 36的平方根是 ,算术平方根是 .
14的平方根是 ,算术平方根是 .
(-4)2的平方根是 ,算术平方根是 .
的平方根是 ,算术平方根是 .
的平方根是 ,算术平方根是 .
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.若x2=16,求5-x的值.
2.一个正数的平方根为x+3与2x-6,求这个正数.
3.填空:
(1)= ,= ,= ,
你能总结出:= .
(2)()2= ,()2= ,
()2= ,
你能总结出:()2= (a≥0).
1.下列说法错误的是 ( )
A. 5是25的算术平方根
B. 1是1的一个平方根
C. (-4)2的平方根是-4
D. 0的平方根与算术平方根都是0
2. 7的平方根是 ,算术平方根是 .
3.±= ,= ,
= .
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
看谁记得最牢
12=1, 112=121, 13=1,
22=4, 122=144, 23=8,
32=9, 132=169, 33=27,
42=16, 142=196, 43=64,
52=25, 152=225, 53=125,
62=36, 162=256, 63=216,
72=49, 172=289, 73=343,
82=64, 182=324, 83=512,
92=81, 192=361, 93=729,
102=100, 202=400, 103=1000.
1.下列说法正确的是 ( )
A.如果一个数有平方根,那么这个数的平方根一定有两个
B.任何一个非负数的平方根都是非负数
C. -a2一定没有平方根
D. a2+1一定有平方根
2. 625的算术平方根是 ,平方根是 .
11的算术平方根是 ,平方根是 .
的算术平方根是 ,平方根是 .
3.计算:
±= ,-= ,
= ,= ,
()2= ,= .
4.求下列各式中的x.
(1)x2=49; (2)x2-144=0.
5.已知2x-1的平方根为±3,3x+y-1的平方根为±4,求x+2y的平方根.
3.1 平方根(2)
1.理解无理数的概念以及常见的几种表现形式,能区分有理数和无理数.
2.会用计算器求平方根,记住常见平方根的估值.
一、 新知探究
阅读教材第108~110页的内容,自主探究,回答下列问题:
1.什么数叫作无理数
2.无理数有哪些表现形式 试举例说明.
3.试着写出用计算器求平方根的按键步骤.
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.下列各数是无理数的是 .
-,,-,-3.14,0.010 010 001…,0.,0,
2.判断下列语句是否正确,并说明原因.
(1)3.787 887 888 788 88是无理数;
(2)无理数可以分为正无理数、负无理数;
(3)无限小数不能化成分数;
(4)无理数是无限小数;
(5)无限小数是无理数;
(6)带有根号的数都是无理数.
3.面积为3的正方形的边长 有理数;
面积为4的正方形的边长 有理数.
(填“是”或“不是”)
4.用计算器求下列各式的值.(精确到0.001)
≈ ,≈ ,
≈ ,≈ .
5.最接近的整数是 ,-最接近的整数是 ,的整数部分是 .
温馨提示:这些都是常用的平方根,记住它们的估计值很有用哦.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.比较下列四个数的大小:5,,4,.
2.已知3a+1的平方根是±4,2a+b-1的平方根是±3,c是的整数部分,求a+2b+c的平方根.
1.下列各数是无理数的是 ( )
A. 0.1 B. C. 0 D.
2.最接近的整数是 ,的整数部分是 .
3.比较大小: 8.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
胡同捉鸡与求算术平方根
不知谁家的鸡跑到胡同里来了.忽然,从一家 ( http: / / www.21cnjy.com )院子里跑出来一个小男孩,他想捉住这只鸡.只见鸡在前面,一会儿快跑,一会儿慢走,小男孩一个劲地在后面追,累得满头大汗,也没有捉住这只鸡.这时候,从胡同的另一头走来一个小女孩,两个人一人把住一头,一步一步地逼近鸡.当两个小孩碰面的时候,鸡无处可逃,终于被捉住了.我们用试凑法求的过程就类似胡同捉鸡.
首先拿1作答案试一试,因为1× HYPERLINK "http://www.21cnjy.com" 1=1,比要小,看来用1作2的算术平方根偏小了.用2试一试,因为2×2=4,比2要大.看来用2作为2的算术平方根偏大了.
经过了两次试验,我们知道的值在1和2之间.
用1.5去试,因为1.5×1.5=2.25 ( http: / / www.21cnjy.com ),也偏大,但是我们看到这个值比1和4都更接近2.再用1.4去试,因为1.4×1.4=1.96,1.96与2仅差0.04,更接近2.必然在1.4和1.5之间,而且靠近1.4.再试1.41,因为1.41×1.41=1.988 1,这个值比2小.再试1.42,因为1.42×1.42=2.016 4,比2大.所以的值在1.41和1.42之间.
这个试算过程可以一直持续下去,一直算到所需要的小数位.
这种“寻找”的想法非常重要,它是用已知去探求、捕捉未知的一种基本方法,在数学中经常会用到.如果把数轴当作一条胡同,把看作跑进胡同里的鸡,用试凑法求的值类似胡同里捉鸡,用两串数把夹在中间,不断缩小两串数的差:
1<<2;1.4<<1.5;1.41<<1.42;1.414<<1.415;1.414 2<<1.414 3;…
需要精确到多少位,就可以精确到多少 ( http: / / www.21cnjy.com )位.用试凑法求平方根,必须从一大一小两边来逼近.不能像小男孩捉鸡那样,一个人只从一面去捉,这样就难以把鸡捉住.
1.下列说法正确的是 ( )
A.带根号的数叫无理数
B.无理数一定是带根号的数
C.无限小数是无理数
D.无理数是无限小数
2.在,,0.020 202…,,2π,中,无理数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
3.用计算器求下列各式的值.
(1)= .(精确到0.001)
(2)25.8的平方根是 .(精确到0.000 1)
4.填空:
(1)若=2,则y= ;
(2)的整数部分是 ,最接近的整数是 .
5.例题:∵<<,即2<<3,∴的整数部分为2,小数部分为(-2).请你观察上述例题后试解下面的问题:
(1)的整数部分是 ,小数部分是 ;
(2)如果的小数部分为a,的小数部分为b,求a+b-5的值.
3.2 立方根
1.理解立方根的意义,会表示立方根.
2.能用立方运算求立方根.
3.会用计算器求立方根.
一、 新知探究
阅读教材第112、113页的内容,自主探究,回答下列问题:
1.请类比平方根的定义及性质,试着写出立方根的定义及性质:
名称 平方根 立方根
定义 若r2=a,则 是 的一个平方根 若b3=a,则 是 的一个立方根
表示方法 (a为被开方数) (a为被开方数)
a>0 有 个值,是 有 个值,是
a=0 有 个值,是 有 个值,是
a<0 (存在/不存在) 有 个值,是
2.试着写出开立方的定义,开立方与立方有什么关系
3.试着写出用计算器求立方根的按键步骤.
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.根据开立方与立方的关系,求下列各数的立方根:
(1)8; (2)0.001; (3)0; (4)-.
学法指导:仿照教材第113页例1完成,注意书写格式.
2.判断下列说法是否正确,并说明理由.
(1)的立方根是±;
(2)-64没有立方根;
(3)8的立方根是2;
(4)互为相反数的两个数的立方根也互为相反数;
(5)互为相反数的两个数的立方也互为相反数.
3.计算:
(1)= ;
(2)= ;
(3)-= ;
(4)-= .
4.用计算器求下列各数的近似值.(精确到0.001)
≈ ;≈ ;≈ .
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.计算:
(1)= ;(2)= .
2.(1)由于= ,因此()3= ;
()3= ,()3= ;
你能总结出:()3= .
(2)由于53= ,因此= ;
= ,= ;
你能总结出:= .
3.求下列各数的值.
(1)8x3+27=0;
(2)(x-1)3-0.343=0.
1. 125的立方根是 ,0.125的立方根是 .
2.计算:= ,= .
3.计算:= ,()3= .
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
立方根近似值的求法
当立方根是一位整数时,很容易求出这 ( http: / / www.21cnjy.com )个立方根;但当立方根是两位或两位以上的整数时,也能容易地求出吗 例如求140 608的立方根,怎样求容易呢
下面就介绍它的巧妙求法.
先用前三位数140来确定立方根的十位数.因为 ( http: / / www.21cnjy.com )53<140<63,所以十位数是5,而不是6.再用最后一位数8来确定立方根的个位数.因为23=8,所以个位数是2.就是说,140 608的立方根是52.确定立方根的个位数时要注意下面规律:我们知道:13=1,43=64,53=125,63=216,93=729,就是说当被开方数的末位数是1,4,5,6,9时,立方根的个位数就等于它本身(1,4,5,6,9).
因为23=8,83=512 ( http: / / www.21cnjy.com ),就是说当被开方数的末位数是8和2时,立方根的个位数就分别是2和8,叫作2与8互换原则;同样还有3与7互换原则(被开方数的末位数分别是3和7,立方根的个位数就分别是7和3).
一般地,如果103
1.下列叙述中,错误的有 ( )
①正数的平方根是正数;
②正数的立方根不一定是正数;
③任意一个正数的立方根都不等于它本身;
④ 0的立方根是0;
⑤-3是27的负的立方根.
A. 1个 B. 2个 C. 3个 D. 4个
2. 2的立方根为 ,-2是 的立方根.-125的立方根为 ,的立方根为 ,的立方根为 .
3.用计算器求下列各数的近似值.(精确到0.01)
≈ ,≈ ,
≈ ,≈ .
4.= ,-= ,
= ,(-)3= ,
= .
5. (1)=3,那么x= .
(2)若b是的小数部分,则-b= .
(3)x是(-)2的平方根,y是64的立方根,则x+y= .
3.3 实数(1)
1.知道实数的概念,掌握实数的分类.
2.理解实数和数轴上的点一一对应的关系.
3.会求实数的相反数与绝对值.
一、 新知探究
阅读教材第116~118页的内容,自主探究,回答下列问题:
1.什么叫作实数,你能对实数按定义进行分类吗 还可以按正负分类吗
2.你知道数轴上的点与实数有什么关系吗
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.把下列各数填在相应的括号里.
0,,-,π,,0.,,,1.313 131,0.101 001 000…
整数有( )
有理数有( )
无理数有( )
负实数有( )
2.下列说法正确的是 ( )
A.实数可以划分为正实数和负实数两大类
B.有理数的相反数是无理数
C.数轴上的每一个点都表示一个有理数
D.每个实数a有且只有一个立方根
3.求出下列各数的相反数和绝对值.
2π - 2- 3.141 5-π
相反数
绝对值
4.若=π,则x= ;若a与互为相反数,则a= ;在数轴上表示-的点到原点的距离为 .
5.如图所示,在数轴上点A,B对应的实数分别为a,b,则有 ( )
A. a+b>0 B. a-b>0
C. ab>0 D. >0
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.下列各组数中互为相反数的是 ( )
A. -2与 B. -2与
C. 2与 D. 与
2.实数a,b在数轴上的位置如图所示,化简:+-.
1.实数可分为 ( )
A.正实数和负实数
B.有理数和无理数
C.小数和分数
D.整数和无理数
2.-的相反数是 ,绝对值是 ;π-3.14的相反数是 ,绝对值是 .
3.实数a,b在数轴上的位置如图所示,则a与b的大小关系是 ( )
A. a>b B. a=b
C. a0
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
“精确值”毫无精确意义
十六世纪,欧洲莱顿地区的 ( http: / / www.21cnjy.com )声道尔夫将π计算到小数点后35位,并且在遗嘱上写明,要后人把这个π的数值刻在他的墓碑上,这就是著名的“π墓志铭”,墓碑上刻下的值是:
3.141 592 653 585 793 238 462 643 383 279 502 88.
随着现代科学技术的发展,借助计算机计算 ( http: / / www.21cnjy.com )π的值就容易得多了.1949年算到2 035位,1958年超过了1万位,1973年超过了300万位,1993年日本的科学家借助先进的计算机,已把π算到了800万位以后.
1979年10月日本人左奇英哲把π的值 ( http: / / www.21cnjy.com )背诵到小数点后两万位,被人们称为“世界上记忆力最强的人”.古代和现代数学家不断有人想要打破π值的纪录,实际上并无多大意义.原苏联数学家格拉维夫斯基证明了π的值即使算到100位都完全没有必要.他算出:假设有一个球体,它的半径等于地球到天狼星的距离R=1.32×1012公里,在这个球中装满了微生物,假定球的每1立方毫米中有1010个微生物,然后把所有微生物排列在一条线上,使每两个相邻微生物的间距等于地球到天狼星的距离,那么,拿这个幻想长度来作为圆的直径,取π的精确值到小数点后100位,可以算出这个巨圆的周长精确到0.000 000 01毫米以下.法国天文学家阿拉哥曾说过“无休止地追求π的精确值,没有丝毫精确意义”.
1.把下列各数填在相应的括号里.
,0.,,,3.14,3.333,0,-3,-2π,0.080 080 008…
整数有( )
有理数有( )
无理数有( )
负实数有( )
2.在实数中 ( )
A.实数的绝对值都是正数
B.有绝对值最大的数,也有绝对值最小的数
C.没有绝对值最大的数,但有绝对值最小的数
D.没有绝对值最大的数,也没有绝对值最小的数
3.下列实数中,无理数是 ( )
A. 5.010 101… B. 2π
C. D.
4. -的相反数是 ,绝对值是 .
π-3的相反数是 ,绝对值是 .
-3的相反数是 ,绝对值是 .
5.实数a,b在数轴上的位置如图所示,则与的大小关系是 .
3.3 实数(2)
1.了解有理数的运算法则、运算律等在实数范围内仍然成立.
2.会比较实数的大小.
3.会计算在实数范围内的简单计算题.
一、 新知探究
阅读教材第118~120页的内容,自主探究,回答下列问题:
1.有理数的运算律在实数范围内仍然成立的有哪些
2.怎么比较两个实数的大小
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.计算:
(1)(-2)+2;
(2)5+2-;
(3)5-3+;
(4)+-.
2.比较大小.
(1)7与4; (2)-3与-2.
3.用计算器计算.(精确到0.01)
(1)π; (2)÷.
4.已知m<-4
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.解下列方程:
(1)3x-=0; (2)-=.
2.比较与的大小.
学法指导:
(1)平方法:把两个数分别平方去掉根号,再比较大小;
(2)估值法:把无理数化成小数形式的估计值,再比较.
3.如图,A表示1,B表示,C到A的距离与B到A的距离相等,求C表示的数.
学法指导:你可以有多少种方法求C表示的数
1.用“>”、“<”、“=”填空.
(1)5 ; (2)-1 0.4.
2.计算:
(1)2-+3;
(2)()2-4×+(-2)3.
3.用计算器计算.(精确到0.01)
(1)×; (2)+.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
实数的性质
实数可实现的基本运算有加、减、乘、 ( http: / / www.21cnjy.com )除、乘方等,对非负数(即正数和0)还可以进行开方运算.实数加、减、乘、除(除数不为零)、平方后结果还是实数.任何实数都可以开奇次方,结果仍是实数,只有非负实数,才能开偶次方其结果还是实数.
四则运算封闭性:实数集R对加、减、乘、除(除数不为零)四则运算具有封闭性,即任意两个实数的和、差、积、商(除数不为零)仍然是实数.
实数集有序性:实数集是有序的,即任意两个实数a、b必定满足下列三个关系之一:a
实数的传递性:实数大小具有传递性,即若a>b,b>c,则有a>c.
实数的阿基米德性:实数具有阿基米德(Archimedes)性,即对任何a,b∈R,若b>a>0,则存在正整数n,使得na>b.
实数的稠密性:实数集R具有稠密性,即两个不相等的实数之间必有另一个实数,既有有理数,也有无理数.
实数唯一性:如果在一条直线(通常为水平直 ( http: / / www.21cnjy.com )线)上确定O作为原点,指定一个方向为正方向(通常把指向右的方向规定为正方向),并规定一个单位长度,则称此直线为数轴.任一实数都对应与数轴上的唯一一个点;反之,数轴上的每一个点也都唯一的表示一个实数.于是,实数集R与数轴上的点有着一一对应的关系.
1.用“>”、“<”、“=”填空.
(1) 3; (2)- -;
(3)3 2; (4) 1.6.
2.比较下列各组数的大小.
(1)-与-2.5;
(2)与.
3.计算:
(1)(-2)+3;
(2)+.
4.用计算器计算.(精确到0.001)
(1)3-π; (2)÷-3.
5.化简:++.
同课章节目录
