解三角形题型归纳 学案

中小学教育资源及组卷应用平台
解三角形题型归纳
班级 姓名
学习目标
1．熟记并能应用正、余弦定理的有关变形公式，解决三角形中的问题．
2．能利用正弦定理、三角恒等变换、三角形面积公式解决较为复杂的三角形问题．
学习过程
自学指导 自学检测及课堂展示
公式默写 1、正弦定理(1)正弦定理： ＝ ＝ ＝2R(R是三角形外接圆的半径)．(2)正弦定理的其他形式①a＝ ，b＝ ，c＝ ；②sinA＝ ，sinB＝ ，sinC＝ ；③a∶b∶c＝ .2、余弦定理(1)余弦定理：a2＝ ，b2＝ ，c2＝ .(2)余弦定理推论：cosA＝ ，cosB＝ ，cosC＝ .3、三角形中的常用公式及变式(1)在△ABC中，A＋B＋C＝π，则A＝π－(B＋C)，＝－，则：sinA＝ ，cosA＝ ，tanA＝ ，sin＝ ， cos＝ . (2)射影定理：a＝ ，b＝ ，c＝ .
三角形的面积公式 4、三角形的面积公式任意三角形的面积公式为：(1)S△ABC＝ ＝ ＝ (2)S△ABC＝ah，其中a为△ABC的一边长，而h为该边上的高的长．(3)S△ABC＝r(a＋b＋c)＝rl，其中r，l分别为△ABC的内切圆半径及△ABC的周长．【即时训练】(1)在△ABC中，已知BC＝6，A＝30°，B＝120°，则△ABC的面积等于 (2)在△ABC中，若a＝3，cos C＝，S△ABC＝4，则b＝________．
题型一、利用正余弦定理求边或角
例1-1、在△ABC中，角A，B，C的对边分别是a，b，c，且.
(1)求； (2)若，求.
例1-2、如图，在平面四边形ABCD中，AD＝1，CD＝2，AC＝．
(1)求cos∠CAD的值； (2)若cos∠BAD＝－，sin∠CBA＝，求BC的长．
变式1、(多选题)在△ABC中，角A，B，C的对边分别是a，b，c，若，，则下列结论正确的是　　
A． B．
C． D．的面积为6
题型二、判断三角形的形状
例2-1、在△ABC中，角A，B，C的对边分别是a，b，c，试判断下列三角形的形状：
(1)；(2)；(3)．
例2-2、在△ABC中，角A，B，C的对边分别是a，b，c，已知
(1)求角的大小；
(2)若的面积，，求的值．
(3)若，试判断的形状．
变式2、(1)在△ABC中，角A，B，C的对边分别是a，b，c，已知且满足，则的形状是　　
A．等腰三角形 B．直角三角形
C．等腰直角三角形 D．等边三角形
(2)在△ABC中,若b2sin2C＋c2sin2B＝2bccosB·cosC，则△ABC的形状为(　　)
A．等边三角形　　 B．等腰直角三角形　　
C．等腰三角形或直角三角形　　 D．直角三角形
题型三、与三角形面积相关问题
例3-1、在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b＋c＝2acos B.
(1)证明：A＝2B；
(2)若△ABC的面积S＝，求角A的大小．
例3-2、△ABC的内角A，B，C的对边分别为a，b，c，已知sin A＋cos A＝0，a＝2，
b＝2.
(1)求c；
(2)设D为BC边上一点，且AD⊥AC，求△ABD的面积．
题型四、几何图形中的解三角形问题
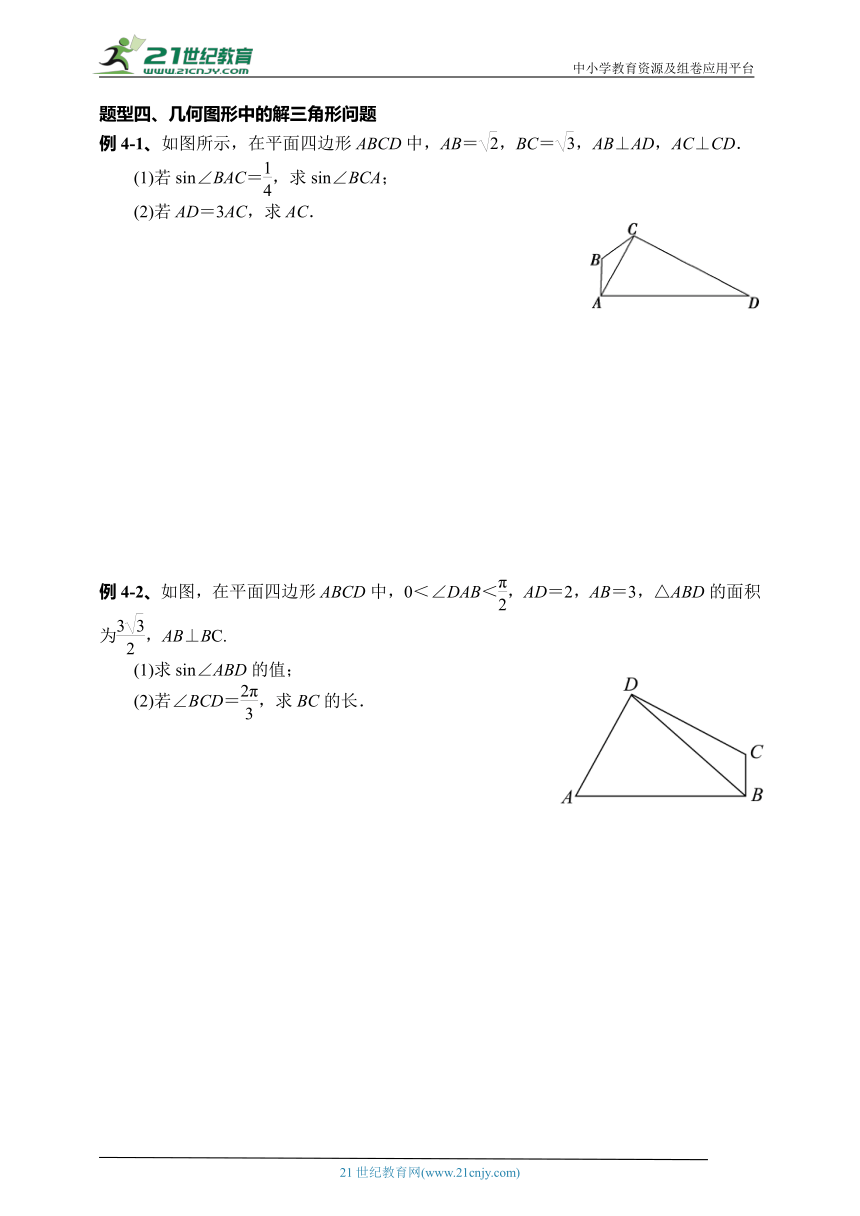
例4-1、如图所示，在平面四边形ABCD中，AB＝，BC＝，AB⊥AD，AC⊥CD．
(1)若sin∠BAC＝，求sin∠BCA；
(2)若AD＝3AC，求AC．
例4-2、如图，在平面四边形ABCD中，0＜∠DAB＜，AD＝2，AB＝3，△ABD的面积为，AB⊥BC.
(1)求sin∠ABD的值；
(2)若∠BCD＝，求BC的长．
*题型五、解三角形中的最值与范围问题
例5-1、已知锐角三角形ABC中，角A，B，C所对的边分别为a，b，c，且c＝2，
2sin＝。
(1)若a＝2，求角A；
(2)求△ABC面积的最大值。
例5-2、在锐角△ABC中，角A，B，C的对边分别是a，b，c，已知2bsin A－a＝0。
(1)求角B的大小；
(2)求cos A＋cos B＋cos C的取值范围。
变式3、在△ABC中，角A，B，C的对边分别是a，b，c，若，的面积等于，则的取值范围是　　
A．， B．，
C．， D．，
课后作业
一、基础训练题
1．在△ABC中，角A，B，C的对边分别是a，b，c，，，，则　　
A． B． C． D．
2．在△ABC中，角A，B，C所对的边分别为a，b，c，若＝，则cosB等于(　　)
A．－　　　　　　　　 B．　　　　　　　　
C．－　　　　　　　　 D．
3．在△ABC中，角A，B，C的对边分别是a，b，c，若a＝b，A＝2B，则cosB＝(　　)
A．　　　　　　　　 B．　　　　　　　　
C．　　　　　　　　 D．
4．在△ABC中，角A，B，C的对边分别是a，b，c，若，，且，则　　
A． B．3
C． D．4
5．△ABC的三个内角A，B，C所对的边分别为a，b，c，若B＝120°，sin C＝，c＝2，则△ABC的面积等于(　　)
A． B．2
C． D．
6．在△ABC中，角A，B，C的对边分别是a，b，c，若，，，则的值为　　
A． B．
C． D．
7．在△ABC中，B＝，BC边上的高等于BC，则cos A＝(　　)
A． B．
C．－ D．－
8．在△ABC中，内角A，B，C的对边分别为a，b，c，若acos B＋bcos A＝4sin C，则△ABC外接圆的面积为(　　)
A．16π B．8π
C．2π D．4π
9．如图，在四边形ABCD中，∠B＝∠C＝120°，AB＝4，BC＝CD＝2，则该四边形的面积等于(　　)
A． B．5
C．6 D．7
10．在△ABC中，若c－acosB＝(2a－b)cosA，则△ABC的形状为(　　)
A．等腰三角形　　 B．等腰直角三角形　　
C．等腰三角形或直角三角形　　 D．直角三角形
11．在△ABC中，内角A，B，C的对边分别为a，b，c，,,
( )
A．1 B．
C． D．
12．(多选题)中，根据下列条件解三角形，其中有一解的是　　
A．，， B．，，
C．，， D．，，
13．(多选题)已知的内角，，所对的边分别为，，，下列四个命题中正确的命题是　　
A．若，则一定是等边三角形
B．若，则一定是等腰三角形
C．若，则一定是等腰三角形
D．若，则一定是锐角三角形
14．在△ABC中，sin A∶sin B∶sin C＝3∶2∶3，则cosC的值为________．
15．已知△ABC中，角A，B，C的对边分别为a，b，c，且满足2cos2A＋sin2A＝2，b＝1，S△ABC＝，则A＝________，＝________．
16．△ABC的内角A，B，C的对边分别为a，b，c，若cos A＝，cos C＝，a＝1，则b＝________．
17．已知△ABC，AB＝AC＝4，BC＝2.点D为AB延长线上一点，BD＝2，连接CD，则△BDC的面积是________，cos∠BDC＝________．
18．如图，已知△ABC中，AB＝，∠ABC＝45°，∠ACB＝60°.
(1)求AC的长；
(2)若CD＝5，求AD的长．
19．如图，在中，是边上一点，，，.
（1）求角的大小；
（2）若，求和.
20．△ABC的内角A，B，C的对边分别为a，b，c，已知2cos C(acos B＋bcos A)＝c.
(1)求C；
(2)若c＝，△ABC的面积为，求△ABC的周长．
21．如图，在△ABC中，AB＝2，cos B＝，点D在线段BC上．
(1)若∠ADC＝，求AD的长．
(2)若BD＝2DC，△ACD的面积为，求的值．
二、综合训练题
22．在△ABC中，已知2acosB＝c，sinAsinB(2－cosC)＝sin2＋，则△ABC为(　　)
A．等边三角形　　 B．等腰直角三角形　　
C．锐角非等边三角形　　 D．钝角三角形
23．在△ABC中，C＝，AB＝3，则△ABC的周长为(　　)
A．6sin＋3　　　 B．6sin＋3　　　
C．2sin＋3　　　 D．2sin＋3
24．如图，在△ABC中，∠C＝，BC＝4，点D在边AC上，AD＝DB，DE⊥AB，E为垂足．若DE＝2，则cosA等于(　　)
A．　　　　　　　　 B．　　　　　　　　
C．　　　　　　　　 D．
25．在△ABC中，角A，B，C的对边分别为a，b，c．已知三个向量m＝，n＝，p＝共线，则△ABC的形状为(　　)
A．等边三角形　　　　 B．等腰三角形　　　　
C．直角三角形　　　　 D．等腰直角三角形
26．如图所示，在四边形ABCD中，AD⊥CD，AD＝10，AB＝14，∠BDA＝60°，
∠BCD＝135°，则BC的长为________．
27．△ABC的内角A，B，C的对边分别为a，b，c．已知△ABC的面积为．
(1)求sin Bsin C；
(2)若6cos Bcos C＝1，a＝3，求△ABC的周长．
三、能力提升题
28．△ABC的内角A，B，C的对边分别为a，b，c ，且，的外接圆半径为，则面积的最大值为　　
A． B．
C． D．
29．(多选题)△ABC的内角A，B，C的对边分别为a，b，c ，知，，则下列判断中正确的是（ ）
A．若，则 B．若该三角形有两解
C．周长的最小值为12 D．面积的最大值
30．(多选题)如图，△ABC的内角A，B，C的对边分别为a，b，c ，为钝角，，，，，则下列结论正确的有　　
A． B．
C． D．的面积为
31．△ABC的内角A，B，C的对边分别为a，b，c ，且，若的面积为，则的最小值为　 　．
32．△ABC的内角A，B，C的对边分别为a，b，c ，且，.
（1）求；
（2）若，边上中线，求的面积.
解三角形题型归纳参考答案
【即时训练】(1)【答案】9
【解析】在△ABC中，由正弦定理，得＝，所以AC＝＝＝6.
又因为C＝180°－120°－30°＝30°，所以S△ABC＝×6×6×＝9.
(2)【答案】2
【解析】∵cos C＝，∴C∈(0°，90°)，∴sin C＝eq \r(1－\b\lc\(\rc\)(\a\vs4\al\co1(\f(1,3))))＝，
又S△ABC＝absin C＝×3×b×＝4，∴b＝2．
题型一、利用正余弦定理求边或角
例1-1、【解】(1)因为，所以，
因为，所以；
(2)因为，由正弦定理可得，
所以，
因为，所以，由正弦定理可得，.
例1-2、【解】(1)在△DAC中，由余弦定理的推论，得cos∠CAD＝＝＝，
所以cos∠CAD＝．
(3)因为∠BAD为四边形内角，所以sin∠BAD＞0，且sin∠CAD＞0，
所以sin∠BAD＝＝，sin∠CAD＝＝，
所以sin∠BAC＝sin(∠BAD－∠CAD)＝sin∠BADcos∠CAD－cos∠BADsin∠CAD
＝×－×＝＋＝，
在△ABC中，由正弦定理得＝，代入数据得BC＝×＝3．
变式1、【答案】ABD
【解析】，，则，故正确；
，．，
，
，又，，，故正确；
，，则由正弦定理得，故错误；
，故正确．
例2-1、【解】（1），，即，
，，或，即或，
为等腰三角形或直角三角形；
（2），，，
，，，
，，即．为等腰三角形．
（3）．边化角，是等腰三角形或是直角角三角形．
例2-2、【解】（1）由得，
即，所以，所以．
（2）由，得．
又，知．由余弦定理可得：，
又由正弦定理得，．．
（3），即
即，，
由（1）得，所以，所以为等边三角形．
变式2、【答案】B
【解析】，
解得，，；
，由正弦定理可得，
，
可得，
，，，，可得，可得是直角三角形．
(2)【答案】D【解析】法一：由＝＝＝2R，
则条件化为：4R2sin2C·sin2B＋4R2sin2C·sin2B＝8R2sinB·sinC·cosB·cosC．
又sinB·sinC≠0，∴sinB·sinC＝cosBcosC，即cos(B＋C)＝0．又0°∴B＋C＝90°，∴A＝90°，故△ABC为直角三角形．
法二：将已知等式变形为：b2(1－cos2C)＋c2(1－cos2B)＝2bccosB·cosC，
即b2＋c2－b2·2－c2·2＝2bc··，
即b2＋c2＝＝＝a2，∴A＝90°，∴△ABC为直角三角形．
例3-1、【解】(1)证明：由正弦定理得sin B＋sin C＝2sin Acos B，
故2sin Acos B＝sin B＋sin(A＋B)＝sin B＋sin Acos B＋cos Asin B，于是sin B＝sin(A－B)．
又A，B∈(0，π)，故0＜A－B＜π，所以B＝π－(A－B)或B＝A－B，
因此A＝π(舍去)或A＝2B，所以A＝2B.
(2)由S＝，得absin C＝，故有sin Bsin C＝sin 2B＝sin Bcos B，
因为sin B≠0，所以sin C＝cos B，又B，C∈(0，π)，所以C＝±B.
当B＋C＝时，A＝；当C－B＝时，A＝.
综上，A＝或A＝.
例3-2、【解】(1)由已知条件可得tan A＝－，A∈(0，π)，所以A＝，
在△ABC中，由余弦定理得28＝4＋c2－4ccos ，
即c2＋2c－24＝0，解得c＝－6(舍去)，或c＝4.
(2)法一：如图，由题设可得∠CAD＝，所以∠BAD＝∠BAC－∠CAD＝，
故△ABD面积与△ACD面积的比值为＝1，
又△ABC的面积为×4×2sin∠BAC＝2，所以△ABD的面积为.
法二：由余弦定理得cos C＝，在Rt△ACD中，cos C＝，
所以CD＝，所以AD＝，DB＝CD＝，
所以S△ABD＝S△ACD＝×2××sin C＝×＝.
法三：∠BAD＝，由余弦定理得cos C＝，所以CD＝，所以AD＝，
所以S△ABD＝×4××sin∠DAB＝.
例4-2、【解】(1)在△ABC中，由正弦定理得＝，
即＝，解得sin∠BCA＝．
(2)设AC＝x，AD＝3x，在Rt△ACD中，CD＝＝2x，sin∠CAD＝＝．
在△ABC中，由余弦定理的推论得，cos∠BAC＝＝．
又∠BAC＋∠CAD＝，所以cos∠BAC＝sin∠CAD，即＝，
整理得3x2－8x－3＝0，解得x＝3或x＝－(舍去)，即AC＝3．
例4-2、【解】(1)因为△ABD的面积S＝AD×ABsin∠DAB＝×2×3sin∠DAB＝，
所以sin∠DAB＝.又0＜∠DAB＜，所以∠DAB＝，所以cos∠DAB＝cos ＝.
由余弦定理得BD＝＝，
由正弦定理得sin∠ABD＝＝.
(2)因为AB⊥BC，所以∠ABC＝，
sin∠DBC＝sin(－∠ABD)＝cos∠ABD＝＝.
在△BCD中，由正弦定理＝可得CD＝＝.
由余弦定理DC2＋BC2－2DC·BCcos∠DCB＝BD2，
可得3BC2＋4BC－5＝0，解得BC＝或BC＝－(舍去)．故BC的长为.
例5-1、【解】(1)因为2sin＝，所以sin＝，
又C∈，所以2C－∈，
所以2C－＝，即C＝，所以＝ sin A＝，
又a(2)在△ABC中，由c2＝a2＋b2－2abcos C，得12＝a2＋b2－ab≥ab，所以S△ABC＝absin C≤3，
当且仅当a＝b，即△ABC为等边三角形时，上式等号成立，
所以△ABC面积的最大值是3。
例5-2、【解】(1)由正弦定理得2sin Bsin A＝sin A，
因为A∈，所以sin A≠0，故sin B＝，因为B∈，所以B＝。
(2)由A＋B＋C＝π得C＝－A，由△ABC是锐角三角形得A∈。
由cos C＝cos＝－cos A＋sin A得，
cos A＋cos B＋cos C＝sin A＋cos A＋＝sin＋。
因为A＋∈，所以sin∈，
则cos A＋cos B＋cos C∈，
故cos A＋cos B＋cos C的取值范围是。
变式3、【答案】D
【解析】的面积，
，，，，
又，由正弦定理，可得，，
，
，，，可得，，
，．
课后作业
1、【答案】A
【解析】利用正弦定理：因为，所以．
2、【答案】B　
【解析】由正弦定理知＝＝1，即tanB＝，由B∈(0，π)，所以B＝，
所以cosB＝cos＝．
3、【答案】B　
【解析】由正弦定理，得sinA＝sinB，又A＝2B，所以sinA＝sin2B＝2sinBcosB，所以cosB＝．
4、【答案】B
【解析】中，若，则，；
又，且，，，
化简得，解得．
5、【答案】A
【解析】解法一：由正弦定理＝，得b＝＝＝。由余弦定理b2＝a2＋c2－2accos B，得7＝a2＋4＋2a，解得a＝1或a＝－3(舍去)，所以S△ABC＝acsin B＝×1×2×＝。
解法二：由正弦定理＝，得b＝＝＝。
因为sin C＝，0°所以sin A＝sin(B＋C)＝sin Bcos C＋cos Bsin C＝×－×＝，
所以S△ABC＝bcsin A＝××2×＝。故选A。
6、【答案】B
【解析】在中，，可得：，
，解得：，①
由余弦定理，可得：，
可得：，②
联立①②，解得：．
7、【答案】C
【解析】设△ABC中角A，B，C的对边分别是a，b，c，由题意可得a＝csin ＝c，则a＝c。
在△ABC中，由余弦定理可得b2＝a2＋c2－ac＝c2＋c2－3c2＝c2，则b＝c。
由余弦定理，可得cos A＝＝＝－。
8、【答案】D
【解析】设△ABC外接圆的半径为R，因为acos B＋bcos A＝4sin C，
所以由正弦定理可得，sin Acos B＋sin Bcos A＝，化简得，sin(A＋B)＝，
在△ABC中，sin(A＋B)＝sin C，解得R＝2，所以△ABC外接圆的面积为S＝πR2＝4π.
9、【答案】B
【解析】连接BD(图略)，在△BCD中，由已知条件，知∠DBC＝＝30°，
∴∠ABD＝90°．在△BCD中，由余弦定理知，BD2＝BC2＋CD2－2BC·CDcos∠C
＝22＋22－2×2×2×cos 120°＝12，∴BD＝2，
∴S四边形ABCD＝S△ABD＋S△BCD＝×4×2＋×2×2×sin 120°＝5．
10、【答案】C　
【解析】∵c－acosB＝(2a－b)cosA，C＝π－(A＋B)，
∴由正弦定理得sinC－sinAcosB＝2sinAcosA－sinBcosA，
∴sinAcosB＋cosAsinB－sinAcosB＝2sinAcosA－sinBcosA，
∴cosA(sinB－sinA)＝0，∴cosA＝0或sinB＝sinA，
∴A＝或B＝A或B＝π－A(舍去)，∴△ABC为等腰或直角三角形．
11、【答案】C
【解析】在中，由正弦定理得：，得，又．
，即，
，又，．
在中，，，
由余弦定理得．
12、【答案】ABD
【解析】、，，，又，
由正弦定理得：，只有一种情况，此时三角形只有一解，合题意；
、，，，
由正弦定理：得：，又，，
只有一解，合题意；
、，，，
由正弦定理得：，无解，不符合题意，
，，；
由正弦定理：得；此时 三角形只有一解，合题意．
13、【答案】AC
【解析】对于，若，则，
即，即，即是等边三角形，故正确；
对于，若，则由正弦定理得，即，则或，即或，则为等腰三角形或直角三角形，故错误；
对于，若，，
即，则是等腰三角形，故正确；
对于，中，，角为锐角，但不一定是锐角三角形，故错误；
14．【答案】　
【解析】由sin A∶sin B∶sin C＝3∶2∶3，可得a∶b∶c＝3∶2∶3．
不妨设a＝3k，b＝2k，c＝3k(k＞0)，则cos C＝＝．
15、【答案】　2　
【解析】∵2cos2A＋sin2A＝2，∴cos2A＋sin2A＝1，∴sin＝，∵0∴2A＋∈，∴2A＋＝，∴A＝．∵b＝1，S△ABC＝＝bcsinA＝×1×c×，∴c＝2，
∴由余弦定理可得，a＝＝＝，∴＝＝＝2．
16、【答案】
【解析】在△ABC中由cos A＝，cos C＝，可得sin A＝，sin C＝，
sin B＝sin(A＋C)＝sin Acos C＋cos Asin C＝，由正弦定理得b＝＝．
17、【答案】　
【解析】由余弦定理得cos∠ABC＝＝，
∴cos∠CBD＝－，sin∠CBD＝，∴S△BDC＝BD·BC·sin∠CBD＝×2×2×＝.
又cos∠ABC＝cos 2∠BDC＝2cos2∠BDC－1＝，0<∠BDC<，∴cos∠BDC＝.
18．【解】(1)在△ABC中，由正弦定理得＝，
则AC＝＝＝3.
(2)因为∠ACB＝60°，所以∠ACD＝120°，
在△ACD中，由余弦定理得，AD＝＝ ＝7.
19、【解】（1）在中，因为，，，
所以.
因为，所以.
（2）因为，，所以.
在中，由余弦定理：，得.
由正弦定理，解得：.
20、【解】(1)由已知及正弦定理，得2cos C(sin Acos B＋sin Bcos A)＝sin C，
2cos Csin(A＋B)＝sin C，故2sin Ccos C＝sin C.
因为C∈(0，π)，所以sin C≠0，所以cos C＝，所以C＝.
(2)由已知，得absin C＝.又C＝，所以ab＝6.
由已知及余弦定理，得c2＝a2＋b2－2abcos C＝7.
故a2＋b2＝13，从而(a＋b)2＝25，即a＋b＝5，所以△ABC的周长为5＋.
21、【解】(1)在△ABC中，∵cos B＝，∴sin B＝．∵∠ADC＝，∴∠ADB＝．
在△ABD中，由正弦定理可得＝，∴AD＝．
(2)∵BD＝2DC，△ACD的面积为，∴S△ABC＝3S△ACD，则4＝×2×BC×，
∴BC＝6，DC＝2．∴由余弦定理得AC＝＝4．
由正弦定理可得＝，∴sin∠BAD＝2sin∠ADB．
又∵＝，∴sin∠CAD＝sin∠ADC．
∵sin∠ADB＝sin∠ADC，∴＝4．
22、【答案】B　
【解析】由2acosB＝c 2a·＝c a2＝b2，所以a＝b．因为sinAsinB(2－cos C)＝sin2＋，
所以2sinAsinB(2－cosC)－2＋1－2sin2＝0，所以2sinAsinB(2－cosC)－2＋cosC＝0，
所以(2－cosC)(2sinAsinB－1)＝0，因为cosC≠2，所以sinAsinB＝，
因为a＝b，所以sin2A＝，所以A＝B＝，所以△ABC是等腰直角三角形，故选B．
【答案】C　
【解析】设△ABC的外接圆半径为R，则2R＝＝2，于是BC＝2RsinA＝2sinA，
AC＝2RsinB＝2sin．于是△ABC的周长为2＋3＝2sin＋3．
24、【答案】C　
【解析】依题意得，BD＝AD＝＝，∠BDC＝∠ABD＋∠A＝2∠A．
在△BCD中，＝，＝×＝，即＝，
由此解得cos A＝．
25、【答案】A　
【解析】∵向量m＝，n＝共线，∴acos＝bcos．
由正弦定理得sinAcos＝sinBcos．∴2sincoscos＝2sincoscos，
∴sin＝sin．∵0<<，0<<，∴＝，∴A＝B．同理可得B＝C，
∴△ABC为等边三角形．故选A．
26、【答案】8　
【解析】在△ABD中，由余弦定理，得AB2＝AD2＋BD2－2AD·BD·cos∠ADB，
设BD＝x，则有142＝102＋x2－2×10xcos 60°，∴x2－10x－96＝0，
∴x1＝16，x2＝－6(舍去)，∴BD＝16．
在△BCD中，由正弦定理知，＝，∴BC＝·sin 30°＝8．
27、【解】(1)由题设得acsin B＝，即csin B＝．
由正弦定理得sin Csin B＝．故sin Bsin C＝．
(2)由题设及(1)得cos Bcos C－sin Bsin C＝－，即cos(B＋C)＝－，
所以B＋C＝，故A＝．
法一：由题设得bcsin A＝，即bc＝8．
由余弦定理得b2＋c2－bc＝9，即(b＋c)2－3bc＝9，得b＋c＝．
故△ABC的周长为a＋b＋c＝3＋．
法二：因为a＝3，所以2R＝＝2(R为△ABC外接圆的半径)，
所以sin Bsin C＝·＝＝＝，则bc＝8．
由余弦定理得b2＋c2－2bc·cos＝9，即b2＋c2－bc＝9，
所以(b＋c)2－3bc＝9，所以(b＋c)2＝9＋3bc＝9＋3×8＝33，故b＋c＝．
所以△ABC的周长为a＋b＋c＝3＋．
28、【答案】D
【解析】的外接圆半径为，
由正弦定理，可得，，
代入已知等式得，
即，，
由此可得，结合，得．
，
（当且仅当时，取等号），
面积为，
当且仅当时，的面积的最大值为．
29、【答案】ABD
【解析】对于A，，，由正弦定理得，
所以，故A正确；对于B，由正弦定理得得，
所以，因为，则有两个解，
所以该三角形有两解，故B正确；对于C，由，
得，
所以，当且仅当时取等号，此时三角形周长最大为等边三角形，
周长为12，故C错误；
对于D，由选项C知，，当且仅当时取等号，
故,所以面积的最大值为，故D正确.
30、【答案】AC
【解析】由，得：，
又角为钝角，解得：，
因为，，由余弦定理，得：，
解得，可知为等腰三角形，即，
所以，解得，故正确，
可得，
在中，，得，可得，故错误，
，可得，可得，故正确，
所以的面积为，故错误．
31、【答案】12
【解析】中，，
由正弦定理得，
即，，，；
又的面积为，；
再由余弦定理可得，
整理可得，
当且仅当时，取等号，，即的最小值为12．
32．【解】（1）由正弦定理有，
因为，有，
因为，故，；
（2）法一：在和中，，
因为，，则，
因为，所以，
所以；
法二：因为，
所以，有，
因为，所以，
所以；
法三：如图，作交于，则是的中点，
所以，，，
即，解得，所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)