2023-2024学年人教版八年级数学下册18.1.2平行四边形的判定同步练习(无答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学下册18.1.2平行四边形的判定同步练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 702.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 12:54:48 | ||
图片预览

文档简介
平行四边形的判定(一)
基础过关
1.下面给出的是四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形 ABCD 是平行四边形的是 ( )
A.3:4:3:4 B.3:3:4:4 C.2:3:4:5 D.3:4:4:3
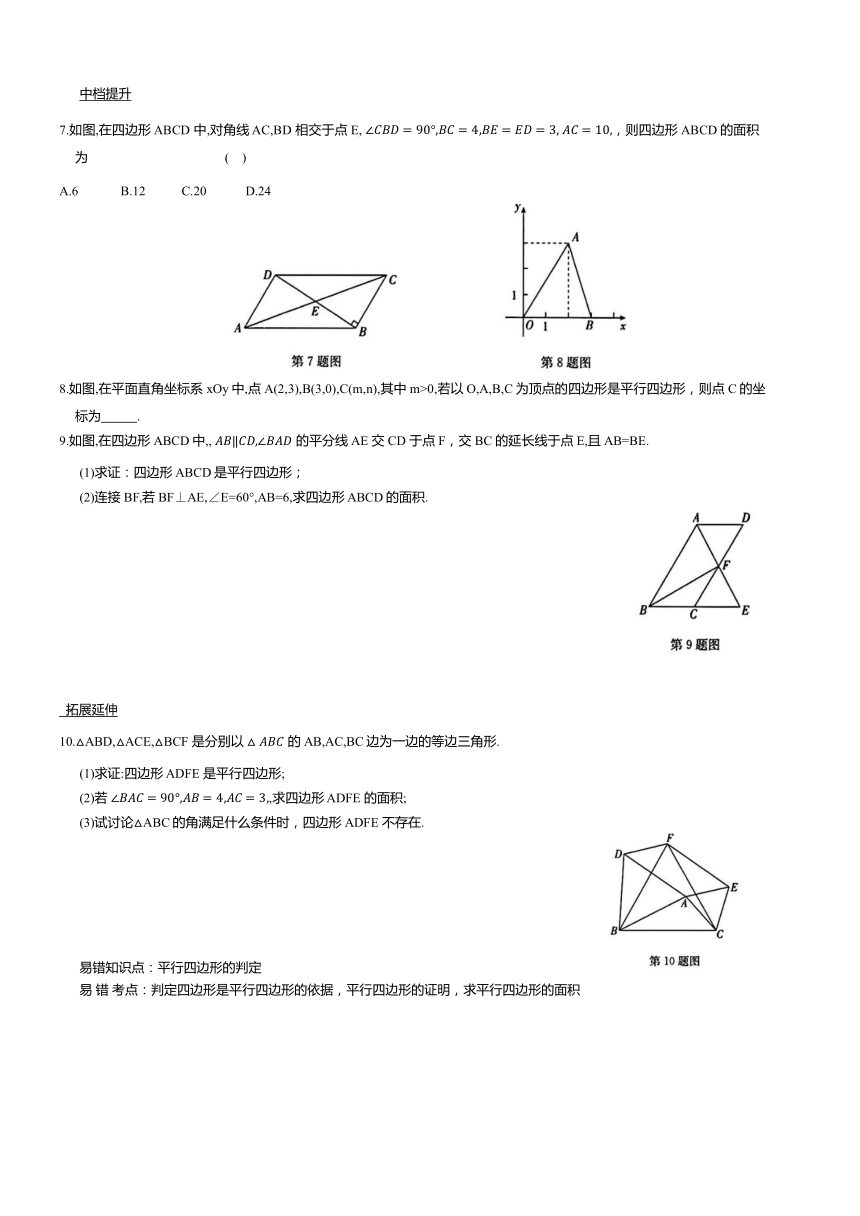
2.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是 ( )
A.8 B.16 C.24 D.32
3.点A,B,C是平面内不在同一条直线上的三点,点 D 是平面内任意一点,若A,B,C,D 四点恰能构成一个平行四边形,则在平面内符合这样条件的点 D有 ( )
A.1个 B.2个 C.3个 D.4个
4.如图,在四边形 ABCD中,AB∥CD,请你添加一个条件,使得四边形 ABCD成为平行四边形,你添加的条件是 .
5.如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点 C,连接CD,BC,则四边形 ABCD 是平行四边形,理由是 .
6.如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形 ACFD是平行四边形.
中档提升
7.如图,在四边形 ABCD 中,对角线 AC,BD 相交于点E, ,则四边形ABCD的面积为 ( )
A.6 B.12 C.20 D.24
8.如图,在平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n),其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
9.如图,在四边形ABCD中,, 的平分线AE 交CD 于点F,交 BC 的延长线于点E,且AB=BE.
(1)求证:四边形 ABCD是平行四边形;
(2)连接BF,若 BF⊥AE,∠E=60°,AB=6,求四边形 ABCD的面积.
拓展延伸
10.△ABD,△ACE,△BCF 是分别以 的AB,AC,BC边为一边的等边三角形.
(1)求证:四边形 ADFE 是平行四边形;
(2)若 ,求四边形 ADFE 的面积;
(3)试讨论△ABC的角满足什么条件时,四边形ADFE 不存在.
易错知识点:平行四边形的判定
易 错 考点:判定四边形是平行四边形的依据,平行四边形的证明,求平行四边形的面积
平行四边形的判定(二)
基础过关
1.如图,小津不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能从商店配到一块与原来相同的玻璃,他带了其中两块玻璃去商店,其编号应该是 ( )
A.①② B.②④ C.③④ D.①③
2.如图,在 ABCD中,E,F 分别是AD,BC边的中点,G,H 是对角线BD上的两点,且 BG=DH,则下列结论中不正确的是 ( )
A. GF⊥FH B. GF=EH C. EF 与AC 互相平分 D. EG=FH
3.如图,在正六边形 ABCDEF 中,M,N 是对角线BE 上的两点.添加下列条件中的一个:①BM=EN;②∠FAN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN 是平行四边形的是 .(填上所有符合要求的条件的序号)
4.已知平面直角坐标系中的三个点的坐标分别为A(2,3),B(6,3),C(4,0),现要找到一点 D,使得这四个点构成的四边形是平行四边形,那么点 D的坐标为 .
5.如图,在四边形 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)请你只添加一个条件(不另加辅助线),使得四边形 AECF 为平行四边形,你添加的条件是 ;
(2)添加了条件后,证明四边形 AECF 为平行四边形.
中档提升
6.如图,在平行四边形 ABCD中, EF、GH的交点P 在BD上,则图中面积相等的平行四边形有 ( )
A.3 对 B.2对 C.1对 D.0对
7.如图,在 ABCD中,已知AD=15 cm,点 P 在AD 边上以1cm/s的速度从点A 向点D 运动,点Q在BC 边上以4 cm/s的速度从点C出发在BC 上往返运动,两个点同时出发,当点 P 到达点D 时停止运动(同时点 Q 也停止运动),设运动时间为t(s)(t>0),若以 P,D,Q,B四点为顶点的四边形是平行四边形,则t的值可以是 .
8.如图,在四边形 ABCD中,AD∥BC(AD>BC),BC=6cm,点P 从点A 出发以1cm/s的速度向点 D运动,同时点Q从点C 出发以2cm/s的速度向点 B 运动(点 Q 运动到点 B 时停止运动).设运动时间为ts,则t= s时,四边形 ABQP 为平行四边形.
9.如图,在 ABCD中,点 E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
拓展延伸
10.如图,△ABC是等边三角形,点 D,F 分别在边 BC,AB上,∠EFB=60°,DC=EF,连接CF,DE,AD,AE.
(1)求证:四边形 EFCD是平行四边形;
(2)若 BF=EF,求证:AE=AD.
易错知识点:平行四边形的性质与判定
易 错 考 点:平行四边形的证明,平行四边形的性质与判定的综合应用
基础过关
1.下面给出的是四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形 ABCD 是平行四边形的是 ( )
A.3:4:3:4 B.3:3:4:4 C.2:3:4:5 D.3:4:4:3
2.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是 ( )
A.8 B.16 C.24 D.32
3.点A,B,C是平面内不在同一条直线上的三点,点 D 是平面内任意一点,若A,B,C,D 四点恰能构成一个平行四边形,则在平面内符合这样条件的点 D有 ( )
A.1个 B.2个 C.3个 D.4个
4.如图,在四边形 ABCD中,AB∥CD,请你添加一个条件,使得四边形 ABCD成为平行四边形,你添加的条件是 .
5.如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点 C,连接CD,BC,则四边形 ABCD 是平行四边形,理由是 .
6.如图,点B,E,C,F在一条直线上,AB=DE,AB∥DE,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形 ACFD是平行四边形.
中档提升
7.如图,在四边形 ABCD 中,对角线 AC,BD 相交于点E, ,则四边形ABCD的面积为 ( )
A.6 B.12 C.20 D.24
8.如图,在平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n),其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点C的坐标为 .
9.如图,在四边形ABCD中,, 的平分线AE 交CD 于点F,交 BC 的延长线于点E,且AB=BE.
(1)求证:四边形 ABCD是平行四边形;
(2)连接BF,若 BF⊥AE,∠E=60°,AB=6,求四边形 ABCD的面积.
拓展延伸
10.△ABD,△ACE,△BCF 是分别以 的AB,AC,BC边为一边的等边三角形.
(1)求证:四边形 ADFE 是平行四边形;
(2)若 ,求四边形 ADFE 的面积;
(3)试讨论△ABC的角满足什么条件时,四边形ADFE 不存在.
易错知识点:平行四边形的判定
易 错 考点:判定四边形是平行四边形的依据,平行四边形的证明,求平行四边形的面积
平行四边形的判定(二)
基础过关
1.如图,小津不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能从商店配到一块与原来相同的玻璃,他带了其中两块玻璃去商店,其编号应该是 ( )
A.①② B.②④ C.③④ D.①③
2.如图,在 ABCD中,E,F 分别是AD,BC边的中点,G,H 是对角线BD上的两点,且 BG=DH,则下列结论中不正确的是 ( )
A. GF⊥FH B. GF=EH C. EF 与AC 互相平分 D. EG=FH
3.如图,在正六边形 ABCDEF 中,M,N 是对角线BE 上的两点.添加下列条件中的一个:①BM=EN;②∠FAN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN 是平行四边形的是 .(填上所有符合要求的条件的序号)
4.已知平面直角坐标系中的三个点的坐标分别为A(2,3),B(6,3),C(4,0),现要找到一点 D,使得这四个点构成的四边形是平行四边形,那么点 D的坐标为 .
5.如图,在四边形 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)请你只添加一个条件(不另加辅助线),使得四边形 AECF 为平行四边形,你添加的条件是 ;
(2)添加了条件后,证明四边形 AECF 为平行四边形.
中档提升
6.如图,在平行四边形 ABCD中, EF、GH的交点P 在BD上,则图中面积相等的平行四边形有 ( )
A.3 对 B.2对 C.1对 D.0对
7.如图,在 ABCD中,已知AD=15 cm,点 P 在AD 边上以1cm/s的速度从点A 向点D 运动,点Q在BC 边上以4 cm/s的速度从点C出发在BC 上往返运动,两个点同时出发,当点 P 到达点D 时停止运动(同时点 Q 也停止运动),设运动时间为t(s)(t>0),若以 P,D,Q,B四点为顶点的四边形是平行四边形,则t的值可以是 .
8.如图,在四边形 ABCD中,AD∥BC(AD>BC),BC=6cm,点P 从点A 出发以1cm/s的速度向点 D运动,同时点Q从点C 出发以2cm/s的速度向点 B 运动(点 Q 运动到点 B 时停止运动).设运动时间为ts,则t= s时,四边形 ABQP 为平行四边形.
9.如图,在 ABCD中,点 E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
拓展延伸
10.如图,△ABC是等边三角形,点 D,F 分别在边 BC,AB上,∠EFB=60°,DC=EF,连接CF,DE,AD,AE.
(1)求证:四边形 EFCD是平行四边形;
(2)若 BF=EF,求证:AE=AD.
易错知识点:平行四边形的性质与判定
易 错 考 点:平行四边形的证明,平行四边形的性质与判定的综合应用
