河北省石家庄市平山县外国语中学2023-2024学年八年级下学期月考数学试题(含答案)
文档属性
| 名称 | 河北省石家庄市平山县外国语中学2023-2024学年八年级下学期月考数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 00:00:00 | ||
图片预览



文档简介
2023-2024学年第二学期阶段练习一
八年级数学(人教版)
说明:1.本练习共6页,满分120分。
2.请将所有答案填写在答题卡上,答在练习卷上无效。
一、选择题(本大题共14个小题,共38分,1~10小题每小题3分11~14小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列式子中,是二次根式的是( )
A. B.
C. D.
2.在中,,则下列式子成立的是( )
A. B.
C. D.
3.计算的结果是( )
A.7 B.
C.-7 D.-49
4.如图:网格中每个正方形边长为1,表示长的线段是( )
A. B.
C. D.
5.若有意义,则的值可以是( )
A.0 B.1 C.2 D.3
6.在平面直角坐标系中,点到原点的距离为( )
A.3 B.4 C.5 D.7
7.下列根式,是最简二次根式的是( )
A. B.
C. D.
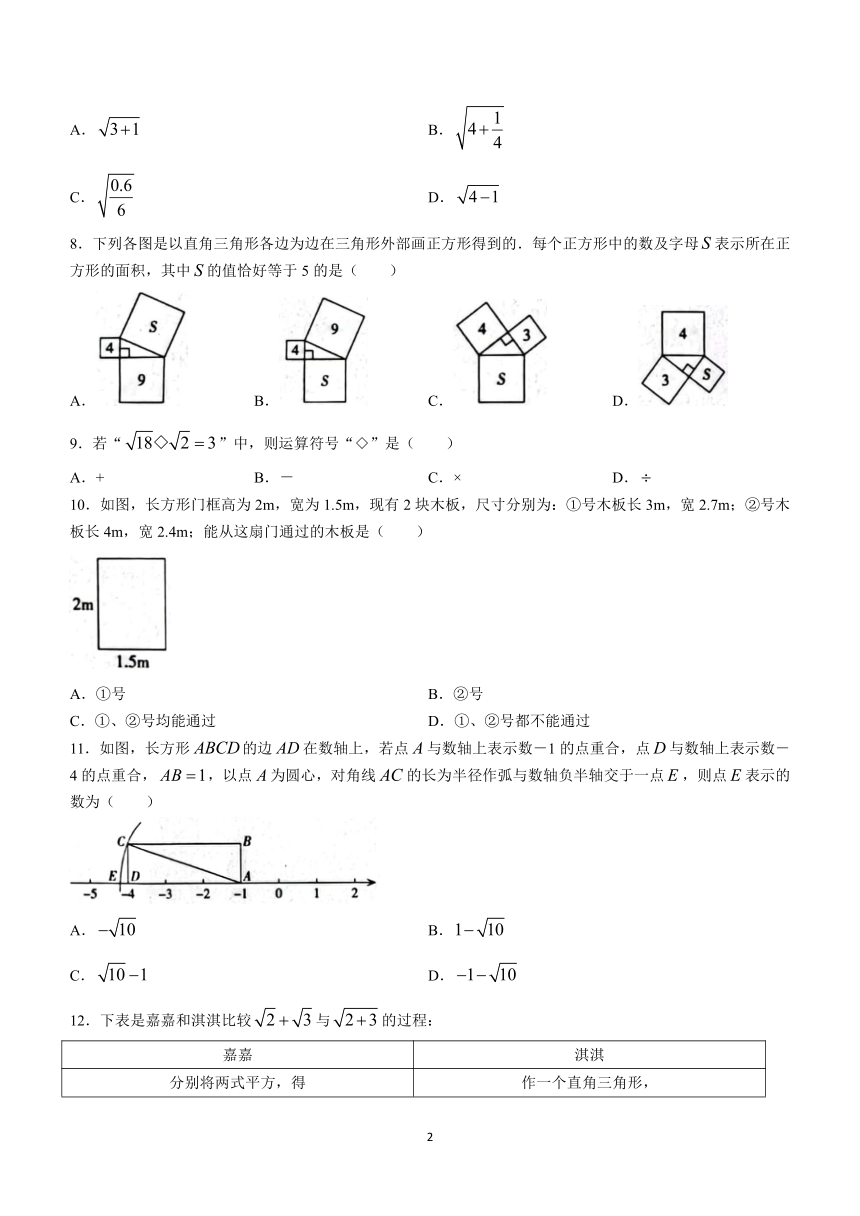
8.下列各图是以直角三角形各边为边在三角形外部画正方形得到的.每个正方形中的数及字母表示所在正方形的面积,其中的值恰好等于5的是( )
A. B. C. D.
9.若“”中,则运算符号“◇”是( )
A.+ B.- C.× D.
10.如图,长方形门框高为2m,宽为1.5m,现有2块木板,尺寸分别为:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;能从这扇门通过的木板是( )
A.①号 B.②号
C.①、②号均能通过 D.①、②号都不能通过
11.如图,长方形的边在数轴上,若点与数轴上表示数-1的点重合,点与数轴上表示数-4的点重合,,以点为圆心,对角线的长为半径作弧与数轴负半轴交于一点,则点表示的数为( )
A. B.
C. D.
12.下表是嘉嘉和淇淇比较与的过程:
嘉嘉 淇淇
分别将两式平方,得,,,. 作一个直角三角形,两直角边长分别为,利用勾股定理,得斜边长为:由三角形中两边之和大于第三边,得.
下列关于两人的思路判断正确的是( )
A.两人都对 B.两人都错
C.嘉嘉错,淇淇对 D.嘉嘉对,淇淇错
13.如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号以每小时16海里的速度向北偏东方向航行,“海天”号以每小时12海里的速度向北偏西一定的角度的航向行驶,它们离港口半小时后分别位于、处,且相距10海里,则“海天”号航行的方向是( )
A.北偏东 B.北偏西
C.北偏西 D.北偏西
14.在解决问题“已知,用含的代数式表示”时,甲的结果是;乙的结果是;丙的结果是,则下列说法正确的是( )
A.甲对 B.乙、丙对
C.甲、乙对 D.甲、乙、丙都对
二、填空题(本大题共3个小题,共10分.15小题2分,16~17小题各4分,每空2分)
15.化简________.
16.已知:
(1)的整数数位是数字________;
(2)代数式________.
17.(1)问题情境一:如图①,一只蚂蚁在一个长为100cm,宽为50cm的长方形地毯上爬行,则线段AC的长是蚂蚁从点A处到达点C处需要走的最短路径,依据是________.
(2)问题情境二:如图②,在情境一中的地毯上堆放着一根正三棱柱的木块,它的侧棱平行且等于地毯的宽AD,木块从正面看是一个边长为10cm的等边三角形,则这只蚂蚁从点A处出发,翻越木块后到达点C处需要走的最短路程是________cm.
三、解答题(本大题共7个小题,满分72分,解答题应写出必要的解题步骤或文字说明)
18.(本小题满分9分)写出下列各命题的逆命题,并判断原命题和逆命题是不是互逆定理.
(1)同位角相等;
(2)全等三角形的对应角相等.
19.(本小题满分9分)
计算:.
解:原式………………………………第1步,
………………………………第2步,
………………………………第3步,
………………………………第4步.
(1)以上解答过程中,从第________步开始出现错误;
(2)请写出本题的正确解答过程.
20.(本小题满分9分)
我国汉代数学家赵爽在证明勾股定理时,创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”.如图,大正方形由4个全等的直角三角形和一个小正方形组成,,.
(1)请你利用这个图形,推导勾股定理:;
(2)若直角三角形的面积为54,,求小正方形的边长.
21.(本小题满分10分)高空抛物严重威胁着人们的“头顶安全”,即便是常见小物件,一旦高空落下,也威力惊人,而且用时很短,常常避让不及.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式(不考虑风速的影响,).
(1)求从40m高空抛物到落地的时间.(结果保留根号)
(2)已知高空抛物动能(单位:J)=10×物体质量(单位:kg)×高度(单位:m),某质量为0.2kg的玩具在高空被抛出后经过4s后落在地上,这个玩具产生的动能会伤害到楼下的行人吗?请说明理由.(注:伤害无防护人体只需要65J的动能)
22.(本小题满分10分)
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面的距离AC为2.4m.
若梯子底端位置保持不动,将梯子斜靠在右墙时,梯子顶端距离地面的距离为1.5m,求小巷有多宽?
23.(本小题满分12分)
嘉琪准备完成题目“计算:”时,发现“■”处的数字印刷不清楚.
(1)他把“■”处的数学猜成-6,请你计算:的结果;
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是.”通过计算说明原题中“■”是几?
24.(本小题满分13分)
如图,在中,,点从点出发,以每秒3个单位长度的速度沿折线运动.设点的运动时间为.
(1)________;
(2)求斜边上的高线长;
(3)①当在上(包含、两点)时,用含的代数式表示的长为________,的取值范围是________;
②若点在的平分线上,求的值.
2023-2024学年第二学期阶段练习一
八年级数学答案(冀教版)
1-5ACCBA 6-10CDBDB 11-14DABD
15.
16.(1)2(2)2024
17.(1)两点之间,线段最短;(2)10
18.解:(1)逆命题:如果两个角相等,那么这两个角是同位角;
由于原命题及逆命题均为假命题,因此原命题和逆命题不是互逆定理;…………5分
(2)逆命题是:如果两个三角形的对应角相等,那么这两个三角形是全等三角形。
由于逆命题为假命题。因此原命题和逆命题不是互逆定理;………………………9分
19.解:(1)3……………………………………………………………………………5分
(2)原式=3
=8+3………………………………………………………………9分
20.解:(1)∵正方形ABCD由4个全等的直角三角形和一个小正方形EFGH组成,AB=c,BE=a,AE=b(b>a),∴c2=4×ab+(b-a)2,
整理,得a2+b2=c2;……………………………………………………………5分
(2)∵直角三角形ABE的面积为54,c=15,
∴ab=54,a2+b2=c2=152=225,∴ab=108,
∴小正方形EFGH的面积=(b-a)2=a2+b2-2ab=225-2×108=9,
∴小正方形EFGH的边长为3.………………………………………………9分
21.解:(1)当h=40m时,(s),………………………………4分
(2)这个玩具产生的动能会伤害到楼下的行人,……………………………………6分
理由如下:当t=4s时,,解得h=80,
∴高空抛物动能=10×0.2×80=160>65,
∴这个玩具产生的动能会伤害到楼下的行人.………………………………………10分
22.解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.………………………………………………………………4分
在Rt△A′BD中,∵∠A′DB=90°,A′D=1.5米,BD2+A′D2=A′B2,
∴BD2+1.52=6.25,……………………………………………………………………8分
∴BD2=4.
∵BD>0,∴BD=2米.∴CD=BC+BD=0.7+2=2.7(米).
答:小巷的宽度CD为2.7米.………………………………………………………10分
23.解:(1)(1-)2-(-6)×+(+2)(-2)
=4-2+6×
=4-2+2-1
=3………………………………………………………………………………6分
(2)设“■”为m,依题意得,
(1-)2-m×+(+2)(-2)=-2
4-2-
m=
∴原题中“■”表示的数字是……………………………………………………12分
24.解:(1)8………………………………………………………………………………3分
(2)如图所示,过点B作BD⊥AC于点D,
∴S△ABC= AB BC=AC BD,
即,
∴斜边AC上的高线长为.
…………………………………………………………………………………………7分
(3)①3t-17,……………………………………………………………9分
②点P在∠BCA的角平分线上时,过点P作PE⊥AC于E,如图所示,
∵CP平分∠BCA,∠B=90°,PE⊥AC,∴PB=PE.
又∵PC=PC,∴Rt△BCP≌Rt△ECP(HL).
∴EC=BC=15,则AE=AC-CE=17-15=2.……………………11分
又∵AP=40-3t,BP=3t-32,∴PE=3t-32.
在Rt△AEP中,AP2=AE2+EP2即(40-3t)2=22+(3t-32)2,
解得.∴点P在∠BAC的平分线上时,.
…………………………………………………………………………………………13分
八年级数学(人教版)
说明:1.本练习共6页,满分120分。
2.请将所有答案填写在答题卡上,答在练习卷上无效。
一、选择题(本大题共14个小题,共38分,1~10小题每小题3分11~14小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列式子中,是二次根式的是( )
A. B.
C. D.
2.在中,,则下列式子成立的是( )
A. B.
C. D.
3.计算的结果是( )
A.7 B.
C.-7 D.-49
4.如图:网格中每个正方形边长为1,表示长的线段是( )
A. B.
C. D.
5.若有意义,则的值可以是( )
A.0 B.1 C.2 D.3
6.在平面直角坐标系中,点到原点的距离为( )
A.3 B.4 C.5 D.7
7.下列根式,是最简二次根式的是( )
A. B.
C. D.
8.下列各图是以直角三角形各边为边在三角形外部画正方形得到的.每个正方形中的数及字母表示所在正方形的面积,其中的值恰好等于5的是( )
A. B. C. D.
9.若“”中,则运算符号“◇”是( )
A.+ B.- C.× D.
10.如图,长方形门框高为2m,宽为1.5m,现有2块木板,尺寸分别为:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;能从这扇门通过的木板是( )
A.①号 B.②号
C.①、②号均能通过 D.①、②号都不能通过
11.如图,长方形的边在数轴上,若点与数轴上表示数-1的点重合,点与数轴上表示数-4的点重合,,以点为圆心,对角线的长为半径作弧与数轴负半轴交于一点,则点表示的数为( )
A. B.
C. D.
12.下表是嘉嘉和淇淇比较与的过程:
嘉嘉 淇淇
分别将两式平方,得,,,. 作一个直角三角形,两直角边长分别为,利用勾股定理,得斜边长为:由三角形中两边之和大于第三边,得.
下列关于两人的思路判断正确的是( )
A.两人都对 B.两人都错
C.嘉嘉错,淇淇对 D.嘉嘉对,淇淇错
13.如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号以每小时16海里的速度向北偏东方向航行,“海天”号以每小时12海里的速度向北偏西一定的角度的航向行驶,它们离港口半小时后分别位于、处,且相距10海里,则“海天”号航行的方向是( )
A.北偏东 B.北偏西
C.北偏西 D.北偏西
14.在解决问题“已知,用含的代数式表示”时,甲的结果是;乙的结果是;丙的结果是,则下列说法正确的是( )
A.甲对 B.乙、丙对
C.甲、乙对 D.甲、乙、丙都对
二、填空题(本大题共3个小题,共10分.15小题2分,16~17小题各4分,每空2分)
15.化简________.
16.已知:
(1)的整数数位是数字________;
(2)代数式________.
17.(1)问题情境一:如图①,一只蚂蚁在一个长为100cm,宽为50cm的长方形地毯上爬行,则线段AC的长是蚂蚁从点A处到达点C处需要走的最短路径,依据是________.
(2)问题情境二:如图②,在情境一中的地毯上堆放着一根正三棱柱的木块,它的侧棱平行且等于地毯的宽AD,木块从正面看是一个边长为10cm的等边三角形,则这只蚂蚁从点A处出发,翻越木块后到达点C处需要走的最短路程是________cm.
三、解答题(本大题共7个小题,满分72分,解答题应写出必要的解题步骤或文字说明)
18.(本小题满分9分)写出下列各命题的逆命题,并判断原命题和逆命题是不是互逆定理.
(1)同位角相等;
(2)全等三角形的对应角相等.
19.(本小题满分9分)
计算:.
解:原式………………………………第1步,
………………………………第2步,
………………………………第3步,
………………………………第4步.
(1)以上解答过程中,从第________步开始出现错误;
(2)请写出本题的正确解答过程.
20.(本小题满分9分)
我国汉代数学家赵爽在证明勾股定理时,创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”.如图,大正方形由4个全等的直角三角形和一个小正方形组成,,.
(1)请你利用这个图形,推导勾股定理:;
(2)若直角三角形的面积为54,,求小正方形的边长.
21.(本小题满分10分)高空抛物严重威胁着人们的“头顶安全”,即便是常见小物件,一旦高空落下,也威力惊人,而且用时很短,常常避让不及.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式(不考虑风速的影响,).
(1)求从40m高空抛物到落地的时间.(结果保留根号)
(2)已知高空抛物动能(单位:J)=10×物体质量(单位:kg)×高度(单位:m),某质量为0.2kg的玩具在高空被抛出后经过4s后落在地上,这个玩具产生的动能会伤害到楼下的行人吗?请说明理由.(注:伤害无防护人体只需要65J的动能)
22.(本小题满分10分)
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面的距离AC为2.4m.
若梯子底端位置保持不动,将梯子斜靠在右墙时,梯子顶端距离地面的距离为1.5m,求小巷有多宽?
23.(本小题满分12分)
嘉琪准备完成题目“计算:”时,发现“■”处的数字印刷不清楚.
(1)他把“■”处的数学猜成-6,请你计算:的结果;
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是.”通过计算说明原题中“■”是几?
24.(本小题满分13分)
如图,在中,,点从点出发,以每秒3个单位长度的速度沿折线运动.设点的运动时间为.
(1)________;
(2)求斜边上的高线长;
(3)①当在上(包含、两点)时,用含的代数式表示的长为________,的取值范围是________;
②若点在的平分线上,求的值.
2023-2024学年第二学期阶段练习一
八年级数学答案(冀教版)
1-5ACCBA 6-10CDBDB 11-14DABD
15.
16.(1)2(2)2024
17.(1)两点之间,线段最短;(2)10
18.解:(1)逆命题:如果两个角相等,那么这两个角是同位角;
由于原命题及逆命题均为假命题,因此原命题和逆命题不是互逆定理;…………5分
(2)逆命题是:如果两个三角形的对应角相等,那么这两个三角形是全等三角形。
由于逆命题为假命题。因此原命题和逆命题不是互逆定理;………………………9分
19.解:(1)3……………………………………………………………………………5分
(2)原式=3
=8+3………………………………………………………………9分
20.解:(1)∵正方形ABCD由4个全等的直角三角形和一个小正方形EFGH组成,AB=c,BE=a,AE=b(b>a),∴c2=4×ab+(b-a)2,
整理,得a2+b2=c2;……………………………………………………………5分
(2)∵直角三角形ABE的面积为54,c=15,
∴ab=54,a2+b2=c2=152=225,∴ab=108,
∴小正方形EFGH的面积=(b-a)2=a2+b2-2ab=225-2×108=9,
∴小正方形EFGH的边长为3.………………………………………………9分
21.解:(1)当h=40m时,(s),………………………………4分
(2)这个玩具产生的动能会伤害到楼下的行人,……………………………………6分
理由如下:当t=4s时,,解得h=80,
∴高空抛物动能=10×0.2×80=160>65,
∴这个玩具产生的动能会伤害到楼下的行人.………………………………………10分
22.解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴AB2=0.72+2.42=6.25.………………………………………………………………4分
在Rt△A′BD中,∵∠A′DB=90°,A′D=1.5米,BD2+A′D2=A′B2,
∴BD2+1.52=6.25,……………………………………………………………………8分
∴BD2=4.
∵BD>0,∴BD=2米.∴CD=BC+BD=0.7+2=2.7(米).
答:小巷的宽度CD为2.7米.………………………………………………………10分
23.解:(1)(1-)2-(-6)×+(+2)(-2)
=4-2+6×
=4-2+2-1
=3………………………………………………………………………………6分
(2)设“■”为m,依题意得,
(1-)2-m×+(+2)(-2)=-2
4-2-
m=
∴原题中“■”表示的数字是……………………………………………………12分
24.解:(1)8………………………………………………………………………………3分
(2)如图所示,过点B作BD⊥AC于点D,
∴S△ABC= AB BC=AC BD,
即,
∴斜边AC上的高线长为.
…………………………………………………………………………………………7分
(3)①3t-17,……………………………………………………………9分
②点P在∠BCA的角平分线上时,过点P作PE⊥AC于E,如图所示,
∵CP平分∠BCA,∠B=90°,PE⊥AC,∴PB=PE.
又∵PC=PC,∴Rt△BCP≌Rt△ECP(HL).
∴EC=BC=15,则AE=AC-CE=17-15=2.……………………11分
又∵AP=40-3t,BP=3t-32,∴PE=3t-32.
在Rt△AEP中,AP2=AE2+EP2即(40-3t)2=22+(3t-32)2,
解得.∴点P在∠BAC的平分线上时,.
…………………………………………………………………………………………13分
同课章节目录
