2023—2024学年人教版数学八年级下册第十九章一次函数单元测试(含简单答案)
文档属性
| 名称 | 2023—2024学年人教版数学八年级下册第十九章一次函数单元测试(含简单答案) | 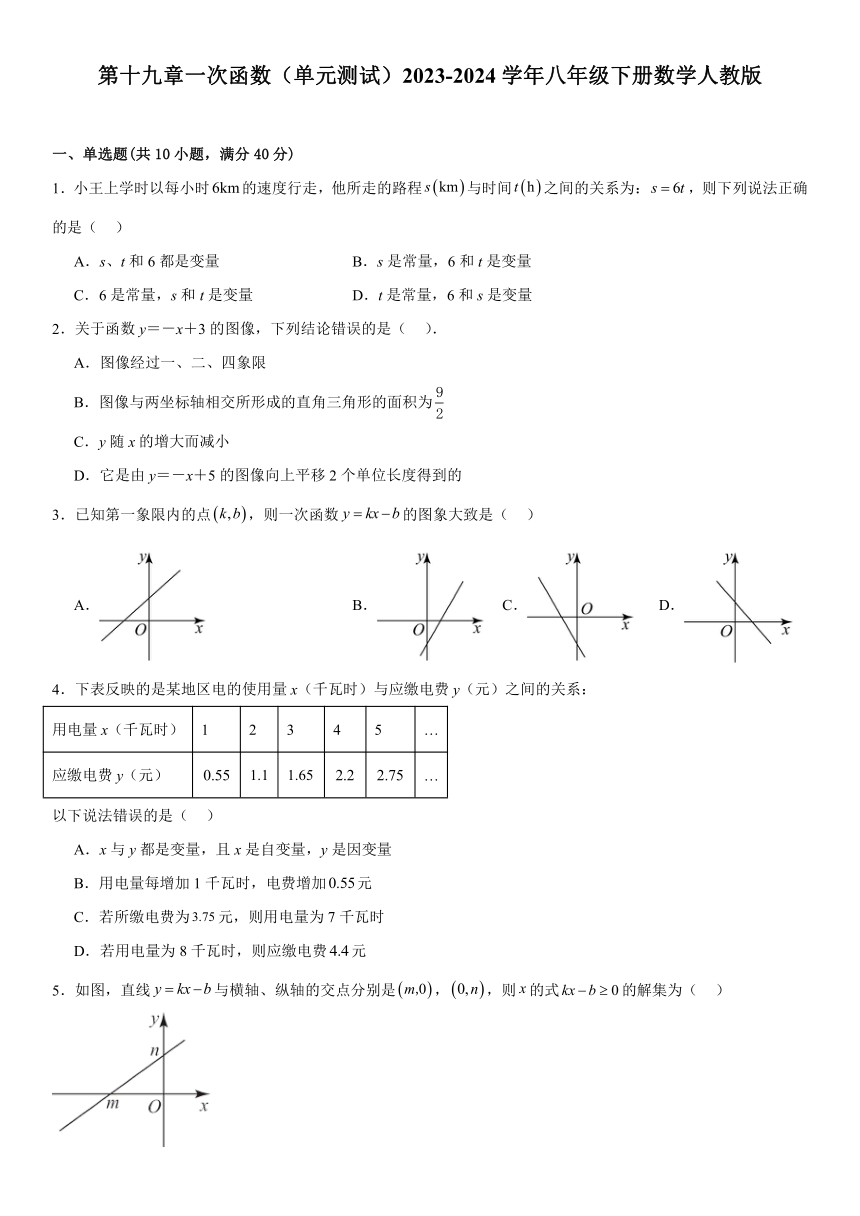 | |
| 格式 | docx | ||
| 文件大小 | 414.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 15:54:55 | ||
图片预览


文档简介
第十九章一次函数(单元测试)2023-2024学年八年级下册数学人教版
一、单选题(共10小题,满分40分)
1.小王上学时以每小时的速度行走,他所走的路程与时间之间的关系为:,则下列说法正确的是( )
A.s、t和6都是变量 B.s是常量,6和t是变量
C.6是常量,s和t是变量 D.t是常量,6和s是变量
2.关于函数y=-x+3的图像,下列结论错误的是( ).
A.图像经过一、二、四象限
B.图像与两坐标轴相交所形成的直角三角形的面积为
C.y随x的增大而减小
D.它是由y=-x+5的图像向上平移2个单位长度得到的
3.已知第一象限内的点,则一次函数的图象大致是( )
A. B. C. D.
4.下表反映的是某地区电的使用量x(千瓦时)与应缴电费y(元)之间的关系:
用电量x(千瓦时) 1 2 3 4 5 …
应缴电费y(元) …
以下说法错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.用电量每增加1千瓦时,电费增加元
C.若所缴电费为元,则用电量为7千瓦时
D.若用电量为8千瓦时,则应缴电费元
5.如图,直线与横轴、纵轴的交点分别是,,则的式的解集为( )
A. B. C. D.
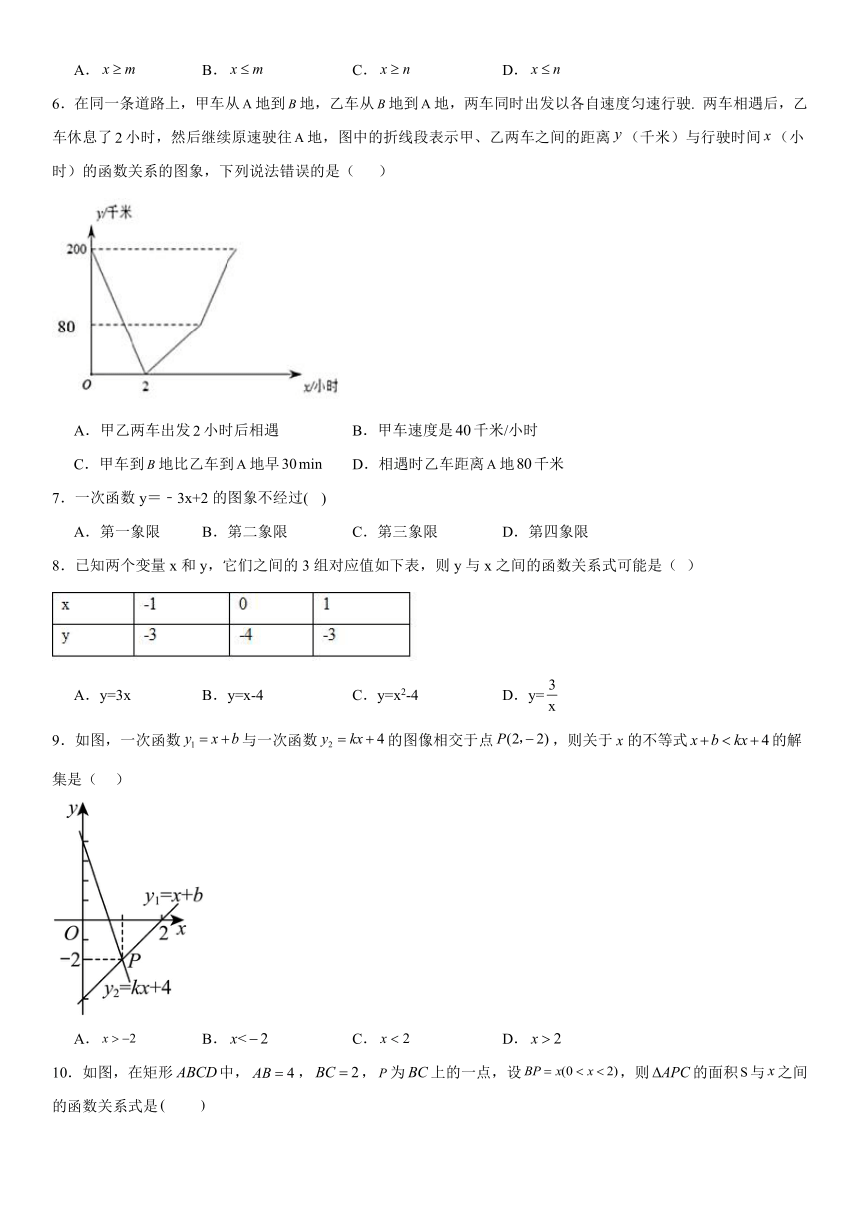
6.在同一条道路上,甲车从地到地,乙车从地到地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了小时,然后继续原速驶往地,图中的折线段表示甲、乙两车之间的距离(千米)与行驶时间(小时)的函数关系的图象,下列说法错误的是( )
A.甲乙两车出发小时后相遇 B.甲车速度是千米/小时
C.甲车到地比乙车到地早 D.相遇时乙车距离地千米
7.一次函数y=﹣3x+2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知两个变量x和y,它们之间的3组对应值如下表,则y与x之间的函数关系式可能是( )
A.y=3x B.y=x-4 C.y=x2-4 D.y=
9.如图,一次函数与一次函数的图像相交于点,则关于x的不等式的解集是( )
A. B. C. D.
10.如图,在矩形中,,,为上的一点,设,则的面积与之间的函数关系式是
A. B. C. D.
二、填空题(共8小题,满分32分)
11.已知直线y=3x﹣2经过点A(a,b),B(a+m,b+k),其中k≠0,则的值为 .
12.如图,直线经过点与直线相交于点,与轴交于,则不等式组的解集为 .
13.已知一次函数的图像经过,则k=
14.已知一次函数图像与y轴交于负半轴,图像上的点,且,请写出一个符合上述条件的一次函数解析式为 .
15.若直线经过第一、二、三象限,则直线不经过第 象限.
16.A、B两地相距12千米,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地.如图的折线OPQ和线段EF分别表示甲、乙两人与A地的距离y甲、y乙与时间x之间的函数关系,且OP与EF相交于点M.下列说法:
①y乙与x的函数关系是y乙=﹣6x+12
②点M表示甲、乙同时出发0.5小时相遇
③甲骑自行车的速度是18千米/小时
④经过或小时,甲、乙两人相距5千米.其中正确的序号有 .
17.如图,已知一次函数y=kx-b与y=x的图像相交于点A(a,1),则关于x的方程的解x= .
18.如图,已知直线a:,直线b:和点,过点P作y轴的平行线交直线a于点,过点作x轴的平行线交直线b于点,过点作y轴的平行线交直线a于点,过点作x轴的平行线交直线b于点,…,按此作法进行下去,则点的横坐标为
三、解答题(共6小题,每题8分,满分48分)
19.已知直线y=2x﹣4交x轴于点A,交y轴于点B,直线y=﹣3x+3交x轴于点C,交y轴于点D,且两直线交于点E.
(1)求点E的坐标;
(2)求S△BDE.
20.已知与成正比,且当时,.
(1)写出与之间的函数表达式;
(2)求当时,求的值.
21.如图,已知一次函数的图象与x轴负半轴交于点A,与正比例函数的图象交于点,且.
(1)求一次函数的表达式;
(2)设中边上的高为h,求h的值.
22.如表是某校七~九年级某月课外兴趣小组(分文艺小组和科技小组)活动时间统计表,其中各年级同一兴趣小组每次活动时间相同.
课外小组活动总时间h 文艺小组活动次数 科技小组活动次数
七年级 12.5 4 3
八年级 10.5 3 3
九年级 7 a b
(1)请你完成以下的分析,求出a,b的值:
观察表格,七、八年级科技小组活动次数相同,文艺小组活动次数相差 次,活动总时间相差 h,由此可知文艺小组每次活动时间为 h,进而可知科技小组每次活动时间为 h;
依题意可得a与b的关系式为 ,因为a与b是自然数,所以a= ,b= ;
(2)若学校重新规定:九年级每月课外兴趣小组活动总次数为8次,在文艺小组与科技小组每次活动时间保持不变的情况下,求出九年级每月课外兴趣小组活动总时间y(h)与文艺小组活动次数x(次)之间的函数关系式(其中规定x为大于1且小于8的自然数).
23.某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
24.如图,在中, , ,,点 D 是边 上的动点(点 D 与点 A、B 不重合),过点 D 作 交射线 于点 E,联结 ,点 F是 的中点,联结、、 .
(1)当点 E在边 上(点 E与点C不重合)时,
①设, ,求出y关于x的函数关系式及定义域;
②当平分时,求出的长;
③求证: 是等边三角形.
(2)如果,请直接写出的长
试卷第1页,共3页
参考答案:
1.C
2.D
3.B
4.C
5.A
6.C
7.C
8.C
9.C
10.D
11.
12.
13.-1
14.(答案不唯一)
15.一
16.①②③
17.3
18.
19.(1)E(,-);(2).
20.(1)
(2)
21.(1)一次函数的表达式为;
(2).
22.(1)1,2,2,1.5;2a+1.5b=7,2,2;(2)y=0.5x+12
23.(1)y=﹣100x+27000;(2)要求当天采摘枇杷的数量不少于草莓的数量,销售总额的最大值为25700元.
24.(1)① ();②(2)1或2
答案第1页,共2页
一、单选题(共10小题,满分40分)
1.小王上学时以每小时的速度行走,他所走的路程与时间之间的关系为:,则下列说法正确的是( )
A.s、t和6都是变量 B.s是常量,6和t是变量
C.6是常量,s和t是变量 D.t是常量,6和s是变量
2.关于函数y=-x+3的图像,下列结论错误的是( ).
A.图像经过一、二、四象限
B.图像与两坐标轴相交所形成的直角三角形的面积为
C.y随x的增大而减小
D.它是由y=-x+5的图像向上平移2个单位长度得到的
3.已知第一象限内的点,则一次函数的图象大致是( )
A. B. C. D.
4.下表反映的是某地区电的使用量x(千瓦时)与应缴电费y(元)之间的关系:
用电量x(千瓦时) 1 2 3 4 5 …
应缴电费y(元) …
以下说法错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.用电量每增加1千瓦时,电费增加元
C.若所缴电费为元,则用电量为7千瓦时
D.若用电量为8千瓦时,则应缴电费元
5.如图,直线与横轴、纵轴的交点分别是,,则的式的解集为( )
A. B. C. D.
6.在同一条道路上,甲车从地到地,乙车从地到地,两车同时出发以各自速度匀速行驶. 两车相遇后,乙车休息了小时,然后继续原速驶往地,图中的折线段表示甲、乙两车之间的距离(千米)与行驶时间(小时)的函数关系的图象,下列说法错误的是( )
A.甲乙两车出发小时后相遇 B.甲车速度是千米/小时
C.甲车到地比乙车到地早 D.相遇时乙车距离地千米
7.一次函数y=﹣3x+2的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知两个变量x和y,它们之间的3组对应值如下表,则y与x之间的函数关系式可能是( )
A.y=3x B.y=x-4 C.y=x2-4 D.y=
9.如图,一次函数与一次函数的图像相交于点,则关于x的不等式的解集是( )
A. B. C. D.
10.如图,在矩形中,,,为上的一点,设,则的面积与之间的函数关系式是
A. B. C. D.
二、填空题(共8小题,满分32分)
11.已知直线y=3x﹣2经过点A(a,b),B(a+m,b+k),其中k≠0,则的值为 .
12.如图,直线经过点与直线相交于点,与轴交于,则不等式组的解集为 .
13.已知一次函数的图像经过,则k=
14.已知一次函数图像与y轴交于负半轴,图像上的点,且,请写出一个符合上述条件的一次函数解析式为 .
15.若直线经过第一、二、三象限,则直线不经过第 象限.
16.A、B两地相距12千米,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地.如图的折线OPQ和线段EF分别表示甲、乙两人与A地的距离y甲、y乙与时间x之间的函数关系,且OP与EF相交于点M.下列说法:
①y乙与x的函数关系是y乙=﹣6x+12
②点M表示甲、乙同时出发0.5小时相遇
③甲骑自行车的速度是18千米/小时
④经过或小时,甲、乙两人相距5千米.其中正确的序号有 .
17.如图,已知一次函数y=kx-b与y=x的图像相交于点A(a,1),则关于x的方程的解x= .
18.如图,已知直线a:,直线b:和点,过点P作y轴的平行线交直线a于点,过点作x轴的平行线交直线b于点,过点作y轴的平行线交直线a于点,过点作x轴的平行线交直线b于点,…,按此作法进行下去,则点的横坐标为
三、解答题(共6小题,每题8分,满分48分)
19.已知直线y=2x﹣4交x轴于点A,交y轴于点B,直线y=﹣3x+3交x轴于点C,交y轴于点D,且两直线交于点E.
(1)求点E的坐标;
(2)求S△BDE.
20.已知与成正比,且当时,.
(1)写出与之间的函数表达式;
(2)求当时,求的值.
21.如图,已知一次函数的图象与x轴负半轴交于点A,与正比例函数的图象交于点,且.
(1)求一次函数的表达式;
(2)设中边上的高为h,求h的值.
22.如表是某校七~九年级某月课外兴趣小组(分文艺小组和科技小组)活动时间统计表,其中各年级同一兴趣小组每次活动时间相同.
课外小组活动总时间h 文艺小组活动次数 科技小组活动次数
七年级 12.5 4 3
八年级 10.5 3 3
九年级 7 a b
(1)请你完成以下的分析,求出a,b的值:
观察表格,七、八年级科技小组活动次数相同,文艺小组活动次数相差 次,活动总时间相差 h,由此可知文艺小组每次活动时间为 h,进而可知科技小组每次活动时间为 h;
依题意可得a与b的关系式为 ,因为a与b是自然数,所以a= ,b= ;
(2)若学校重新规定:九年级每月课外兴趣小组活动总次数为8次,在文艺小组与科技小组每次活动时间保持不变的情况下,求出九年级每月课外兴趣小组活动总时间y(h)与文艺小组活动次数x(次)之间的函数关系式(其中规定x为大于1且小于8的自然数).
23.某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
24.如图,在中, , ,,点 D 是边 上的动点(点 D 与点 A、B 不重合),过点 D 作 交射线 于点 E,联结 ,点 F是 的中点,联结、、 .
(1)当点 E在边 上(点 E与点C不重合)时,
①设, ,求出y关于x的函数关系式及定义域;
②当平分时,求出的长;
③求证: 是等边三角形.
(2)如果,请直接写出的长
试卷第1页,共3页
参考答案:
1.C
2.D
3.B
4.C
5.A
6.C
7.C
8.C
9.C
10.D
11.
12.
13.-1
14.(答案不唯一)
15.一
16.①②③
17.3
18.
19.(1)E(,-);(2).
20.(1)
(2)
21.(1)一次函数的表达式为;
(2).
22.(1)1,2,2,1.5;2a+1.5b=7,2,2;(2)y=0.5x+12
23.(1)y=﹣100x+27000;(2)要求当天采摘枇杷的数量不少于草莓的数量,销售总额的最大值为25700元.
24.(1)① ();②(2)1或2
答案第1页,共2页
