山东省聊城颐中外国语学校2023-2024学年高二下学期第一次质量检测数学试题(含解析)
文档属性
| 名称 | 山东省聊城颐中外国语学校2023-2024学年高二下学期第一次质量检测数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 423.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 18:07:41 | ||
图片预览




文档简介
颐中外国语学校2023-2024学年高二下学期第一次质量检测
数学试题 考试时间:120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题:本题共8小题,每小题5分,共40分。在每个小题给出的选项中,只有一项是符合题目要求的。
1.一对夫妻带着3个小孩和一个老人,手拉着手围成一圈跳舞,3个小孩不相邻的站法种数是
A.6 B.12 C.18 D.36
2.函数的单调递减区间是
A. B. C. D.和
3.在的展开式中,的系数为
A.10 B. C.20 D.
4.将8个大小形状完全相同的小球放入3个不同的盒子中,要求每个盒子中至少放2个小球,则不同放法的种数为
A.3 B.6 C.10 D.15
5.已知函数,有大于零的极值点,则的取值范围为
A. B.
C. D.
6.若函数是上的增函数,则实数a的取值范围是
A. B.
C. D.
7.某班计划从3位男生和4位女生中选出2人参加辩论赛,并且至少1位女生入选,则不同的选法的种数为
A.12 B.18 C.21 D.24
8.若一个五位数的各个数位上的数字之和为3,则这样的五位数共有( )个.
A. B.20 C.10 D.12
多选题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的,得6分,部分选对的得部分分,有选错的得0分。
9.下列说法正确的是
A.可表示为
B.若把单词“best”的字母顺序写错,则可能出现的错误共有23种
C.9个朋友聚会,见面后每两人握手一次,一共握手36次
D.5个人站成一排,甲不站排头,乙不站排尾,共有72种不同排法
10.关于二项式的展开式,下列选项正确的有
A.总共有6项 B.存在常数项C.项的系数是40 D.二项式系数之和为32
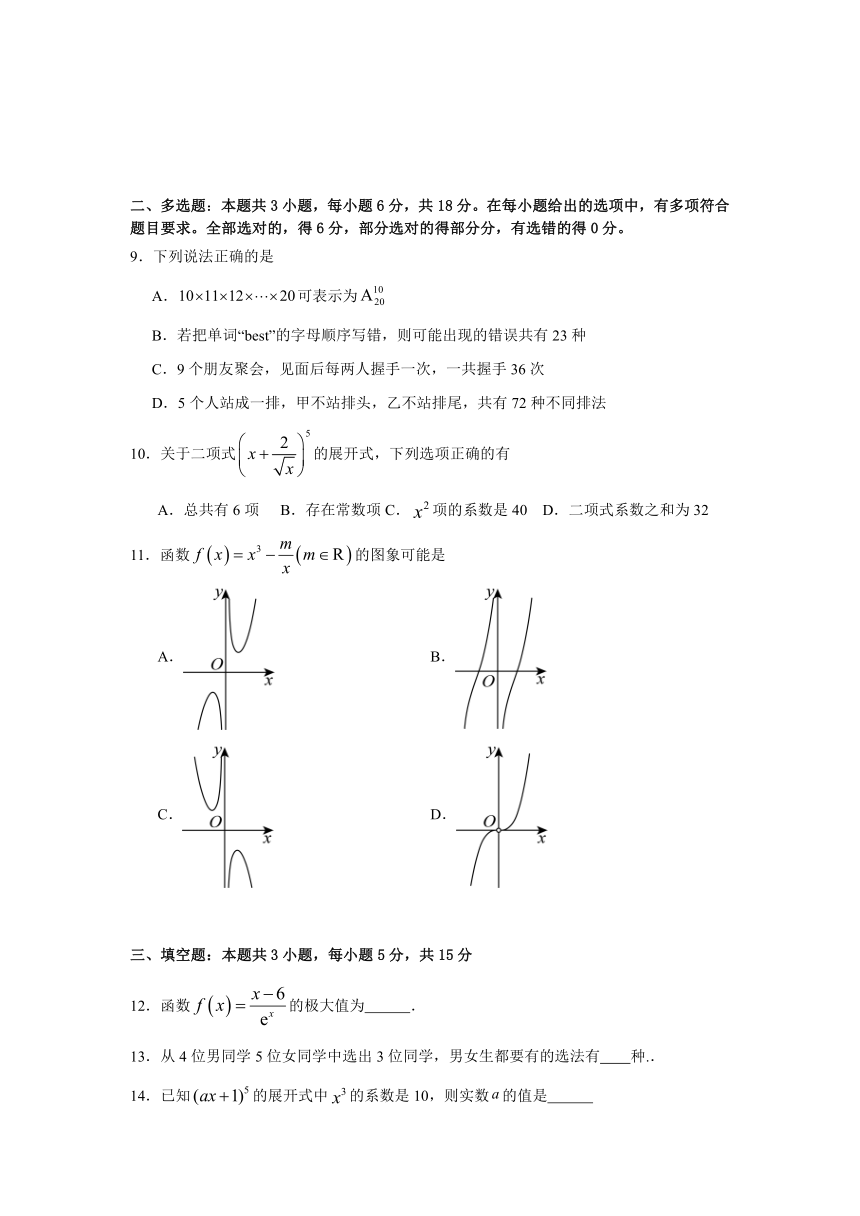
11.函数的图象可能是
A. B.
C. D.
填空题:本题共3小题,每小题5分,共15分
12.函数的极大值为 .
13.从4位男同学5位女同学中选出3位同学,男女生都要有的选法有 种..
14.已知的展开式中的系数是10,则实数的值是
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知二项式的展开式中共有10项.
(1)求展开式的第5项的二项式系数;
(2)求展开式中含的项.
16.(15分)从4名男生和3名女生中各选2人,
(1)共有多少种不同的选法?
(2)如果男生甲与女生乙至少要有1人被选中,那么有多少种不同选法?
(3)选出的4人参加百米接力赛,男生甲和女生乙同时被选中参赛,且甲不能跑第一棒,乙不能跑最后一棒,有多少种不同的安排方法?(用数字作答)
17.(15分)已知函数.
(1)若,求实数的值;
(2)求函数的单调区间.
18.(17分)已知曲线在点处的切线的斜率为3,且当时,函数取得极值.
(1)求函数在点处的切线方程;
(2)求函数的极值;
(3)若存在,使得不等式成立,求m的取值范围.
19(17分).某届世界杯足球赛决赛,共有32个队入围.他们先分成8个小组进行单循环赛,决出16强(各小组取前两名),然后这16强按照确定的程序进行淘汰赛,最后决出冠、亚军和第三、第四名.问
(1)第一阶段分8个小组进行单循环赛,决出16强,需要安排多少场比赛?最多需准备多少比赛场馆?
第二阶段进行淘汰赛,最后决出冠、亚军和第三、四名共安排了多少场比赛?
颐中外国语学校2023-2024学年高二下学期第一次质量检测
数学试题 参考答案:
1.B【详解】将老人位置固定,夫妻两人在老人左右,此时有种站法,
将三个孩子插入两两大人之间的空隙中,有种站法,
故总的站法有.故选:B
2.C【分析】求出导函数,令即可得解.
【详解】,
令,得,所以函数的单调递减区间是.故选:C.
3.D【分析】求出展开式的通项,再令的指数等于即可得解.
【详解】展开式的通项为,
令,则的系数为.故选:D.
4.B【分析】对每个盒子放入2个球,再看余下2个球的去向即可得解.
【详解】依题意,每个盒子放入2个球,余下2个球可以放入一个盒子有种方法,放入两个盒子有种方法,所以不同放法的种数为.故选:B
5.D【分析】由极值点的定义结合函数与方程参变分离即可求解.
【详解】由题意有正根,即方程有正根,
而当时,,所以的取值范围为.故选:D.
6.C【分析】根据函数给定区间上为增函数可得导函数在该区间上恒为非负数,利用参变分离法即可通过求相应函数的最值求得参数范围.
【详解】因为函数是上的增函数,所以在上恒成立,
即在上恒成立.令,,则,
则当时,,当时,,故在上单调递减,在上单调递增,所以,所以.故选:C.
7.B
8.A【分析】分三种情况讨论,再利用分步计数原理排数字,即可求解.
【详解】若一个五位数的各个数位上的数字之和为3,则这样的五位数可分为类:
第一类,五位数的各个数位上的数字是个,个组成,
则由首位不为可知,在首位,其余各位为,即,仅有种方法;
第二类,五位数的各个数位上的数字是个,个,个组成,
则由首位不为可知,或在首位,选个放在首位,另个则从其它个位选个位放上,其余各位为,共有种方法;
第三类,五位数的各个数位上的数字是个,个组成,
则由首位不为可知,在首位,在其它个位中选个位为,其余各位为,共有种方法;所以由分类计数原理可得共有个这样的五位数.故选:A
9.BC【分析】根据排列数公式计算即可判断A;利用排列即可判断B;从9人种选2人结合组合即可判断C;利用排除法即可判断D.
【详解】对于A,因为,故A错误;
对于B,可能出现的错误共有,故B正确;
对于C,9个朋友聚会,两人握手一次,则共有次,故C正确;
对于D,若5个人站成一排,则有种,
若甲站排头,则有种,
若乙站排尾,则有种,
若甲站排头且乙站排尾,则有种,
所以甲不站排头,乙不站排尾,共有种不同排法,故D错误.故选:BC.
10.ACD根据二项展开式以及二项式系数的概念,逐项分析判断即可得解.
【详解】根据二项展开式的通项公式可得:
,
对A,由指数为,展开式共有项,A正确;
对B,由,若要存在常数项即有解,
此时,不符题意,不存在常数项,故B错误;
对C,令,解得,此时,,故C正确;
对D,由二项式系数和为,故D正确.故选:ACD
11.ABD【详解】由题意可知,函数的定义域为,
当时,,函数在上单调递增,故B正确;
当时,,,所以在上单调递增,故D正确;
当时,当时,;当时,;
故A正确;C错误.故选:ABD.
12./
【详解】,当时,,当时,.
所以在上单调递增,在上单调递减,
所以的极大值为.故答案为:
13.70【详解】若选出的1男2女,此时选法有种,若选出的2男1女,此时选法有种,故男女生都要有的选法有种.
14.1【分析】根据条件,求出的系数,列出关于的方程,求出a的值.
【详解】因为的展开式的通项为,
又的展开式中的系数是10,所以,即,所以,则.
15.(1)126(2)
【分析】(1)根据项数可求得,根据二项式系数与项数之间关系列出等式,解出即可;
(2)由(1)中的,求出通项,使的幂次为4,求出含的项即可.
【详解】(1)解:因为二项式的展开式中共有10项,所以,
所以第5项的二项式系数为;
(2)由(1)知,记含的项为第项,
所以,
取,解得,所以,
故展开式中含的项为.
16.(1)18(2)15(3)84【详解】(1)根据题意,从4名男生和3名女生中各选2人,
男生有种选法,女生有种选法,故选法有种;
(2)根据题意,分3种情况讨论:
男生甲被选中,女生乙没有被选中,有种.
男生甲没有被选中,女生乙被选中,有种,
男生甲和女生乙被选中,有种,
则共有种选法.
(3)男生甲和女生乙同时被选中的选法为种,
4人参加百米接力赛的总安排方法为种,
甲跑第一棒的安排方法为种,
乙跑最后一棒的安排方法为种,
甲跑第一棒且乙跑最后一棒的安排方法为种,
甲不能跑第一棒,乙不能跑最后一棒的安排方法为种.
17.(1)(2)当时,的单调递增区间为,无单调递减区间;
当时,的单调递增区间为,单调递减区间为.
【详解】(1),
因为,所以.
(2)函数的定义域为.
,
当时,恒成立,
所以的单调递增区间为,无单调递减区间;
当时,令解得,
的解集为,
的解集为,
所以的单调递增区间为,单调递减区间为.
综上所述:当时,的单调递增区间为,无单调递减区间;
当时,的单调递增区间为,单调递减区间为.
18.(1)(2)的极大值为极小值为(3)
【详解】(1)由题得:,
结合题意可得,
解得,经检验符合题意,
故,,
所以在点处的切线方程为.
(2)由(1)知.
令,解得或,
令,解得,
故在,上单调递增,在上单调递减,
所以的极大值为,
的极小值为;
(3)在上有极大值,无极小值,
又因为,,所以,
所以要使不等式能成立,则.
所以,
故取值范围是.
19.(1)48,16 (2)
【详解】(1)第一阶段每个小组有4个队,进行单循环赛需安排场比赛.
合计需安排场比赛.
即使所有队同时开始比赛,最多需个场馆.
(2)第二阶段进行淘汰赛,由16支队决出前4强需要场比赛.
剩下前4强,需有2场比赛,
首先决出前2名,再有1场比赛决出冠、亚军,再1场比赛决出第三、第四名.
所以16强共计需要场比赛
数学试题 考试时间:120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题:本题共8小题,每小题5分,共40分。在每个小题给出的选项中,只有一项是符合题目要求的。
1.一对夫妻带着3个小孩和一个老人,手拉着手围成一圈跳舞,3个小孩不相邻的站法种数是
A.6 B.12 C.18 D.36
2.函数的单调递减区间是
A. B. C. D.和
3.在的展开式中,的系数为
A.10 B. C.20 D.
4.将8个大小形状完全相同的小球放入3个不同的盒子中,要求每个盒子中至少放2个小球,则不同放法的种数为
A.3 B.6 C.10 D.15
5.已知函数,有大于零的极值点,则的取值范围为
A. B.
C. D.
6.若函数是上的增函数,则实数a的取值范围是
A. B.
C. D.
7.某班计划从3位男生和4位女生中选出2人参加辩论赛,并且至少1位女生入选,则不同的选法的种数为
A.12 B.18 C.21 D.24
8.若一个五位数的各个数位上的数字之和为3,则这样的五位数共有( )个.
A. B.20 C.10 D.12
多选题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的,得6分,部分选对的得部分分,有选错的得0分。
9.下列说法正确的是
A.可表示为
B.若把单词“best”的字母顺序写错,则可能出现的错误共有23种
C.9个朋友聚会,见面后每两人握手一次,一共握手36次
D.5个人站成一排,甲不站排头,乙不站排尾,共有72种不同排法
10.关于二项式的展开式,下列选项正确的有
A.总共有6项 B.存在常数项C.项的系数是40 D.二项式系数之和为32
11.函数的图象可能是
A. B.
C. D.
填空题:本题共3小题,每小题5分,共15分
12.函数的极大值为 .
13.从4位男同学5位女同学中选出3位同学,男女生都要有的选法有 种..
14.已知的展开式中的系数是10,则实数的值是
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)已知二项式的展开式中共有10项.
(1)求展开式的第5项的二项式系数;
(2)求展开式中含的项.
16.(15分)从4名男生和3名女生中各选2人,
(1)共有多少种不同的选法?
(2)如果男生甲与女生乙至少要有1人被选中,那么有多少种不同选法?
(3)选出的4人参加百米接力赛,男生甲和女生乙同时被选中参赛,且甲不能跑第一棒,乙不能跑最后一棒,有多少种不同的安排方法?(用数字作答)
17.(15分)已知函数.
(1)若,求实数的值;
(2)求函数的单调区间.
18.(17分)已知曲线在点处的切线的斜率为3,且当时,函数取得极值.
(1)求函数在点处的切线方程;
(2)求函数的极值;
(3)若存在,使得不等式成立,求m的取值范围.
19(17分).某届世界杯足球赛决赛,共有32个队入围.他们先分成8个小组进行单循环赛,决出16强(各小组取前两名),然后这16强按照确定的程序进行淘汰赛,最后决出冠、亚军和第三、第四名.问
(1)第一阶段分8个小组进行单循环赛,决出16强,需要安排多少场比赛?最多需准备多少比赛场馆?
第二阶段进行淘汰赛,最后决出冠、亚军和第三、四名共安排了多少场比赛?
颐中外国语学校2023-2024学年高二下学期第一次质量检测
数学试题 参考答案:
1.B【详解】将老人位置固定,夫妻两人在老人左右,此时有种站法,
将三个孩子插入两两大人之间的空隙中,有种站法,
故总的站法有.故选:B
2.C【分析】求出导函数,令即可得解.
【详解】,
令,得,所以函数的单调递减区间是.故选:C.
3.D【分析】求出展开式的通项,再令的指数等于即可得解.
【详解】展开式的通项为,
令,则的系数为.故选:D.
4.B【分析】对每个盒子放入2个球,再看余下2个球的去向即可得解.
【详解】依题意,每个盒子放入2个球,余下2个球可以放入一个盒子有种方法,放入两个盒子有种方法,所以不同放法的种数为.故选:B
5.D【分析】由极值点的定义结合函数与方程参变分离即可求解.
【详解】由题意有正根,即方程有正根,
而当时,,所以的取值范围为.故选:D.
6.C【分析】根据函数给定区间上为增函数可得导函数在该区间上恒为非负数,利用参变分离法即可通过求相应函数的最值求得参数范围.
【详解】因为函数是上的增函数,所以在上恒成立,
即在上恒成立.令,,则,
则当时,,当时,,故在上单调递减,在上单调递增,所以,所以.故选:C.
7.B
8.A【分析】分三种情况讨论,再利用分步计数原理排数字,即可求解.
【详解】若一个五位数的各个数位上的数字之和为3,则这样的五位数可分为类:
第一类,五位数的各个数位上的数字是个,个组成,
则由首位不为可知,在首位,其余各位为,即,仅有种方法;
第二类,五位数的各个数位上的数字是个,个,个组成,
则由首位不为可知,或在首位,选个放在首位,另个则从其它个位选个位放上,其余各位为,共有种方法;
第三类,五位数的各个数位上的数字是个,个组成,
则由首位不为可知,在首位,在其它个位中选个位为,其余各位为,共有种方法;所以由分类计数原理可得共有个这样的五位数.故选:A
9.BC【分析】根据排列数公式计算即可判断A;利用排列即可判断B;从9人种选2人结合组合即可判断C;利用排除法即可判断D.
【详解】对于A,因为,故A错误;
对于B,可能出现的错误共有,故B正确;
对于C,9个朋友聚会,两人握手一次,则共有次,故C正确;
对于D,若5个人站成一排,则有种,
若甲站排头,则有种,
若乙站排尾,则有种,
若甲站排头且乙站排尾,则有种,
所以甲不站排头,乙不站排尾,共有种不同排法,故D错误.故选:BC.
10.ACD根据二项展开式以及二项式系数的概念,逐项分析判断即可得解.
【详解】根据二项展开式的通项公式可得:
,
对A,由指数为,展开式共有项,A正确;
对B,由,若要存在常数项即有解,
此时,不符题意,不存在常数项,故B错误;
对C,令,解得,此时,,故C正确;
对D,由二项式系数和为,故D正确.故选:ACD
11.ABD【详解】由题意可知,函数的定义域为,
当时,,函数在上单调递增,故B正确;
当时,,,所以在上单调递增,故D正确;
当时,当时,;当时,;
故A正确;C错误.故选:ABD.
12./
【详解】,当时,,当时,.
所以在上单调递增,在上单调递减,
所以的极大值为.故答案为:
13.70【详解】若选出的1男2女,此时选法有种,若选出的2男1女,此时选法有种,故男女生都要有的选法有种.
14.1【分析】根据条件,求出的系数,列出关于的方程,求出a的值.
【详解】因为的展开式的通项为,
又的展开式中的系数是10,所以,即,所以,则.
15.(1)126(2)
【分析】(1)根据项数可求得,根据二项式系数与项数之间关系列出等式,解出即可;
(2)由(1)中的,求出通项,使的幂次为4,求出含的项即可.
【详解】(1)解:因为二项式的展开式中共有10项,所以,
所以第5项的二项式系数为;
(2)由(1)知,记含的项为第项,
所以,
取,解得,所以,
故展开式中含的项为.
16.(1)18(2)15(3)84【详解】(1)根据题意,从4名男生和3名女生中各选2人,
男生有种选法,女生有种选法,故选法有种;
(2)根据题意,分3种情况讨论:
男生甲被选中,女生乙没有被选中,有种.
男生甲没有被选中,女生乙被选中,有种,
男生甲和女生乙被选中,有种,
则共有种选法.
(3)男生甲和女生乙同时被选中的选法为种,
4人参加百米接力赛的总安排方法为种,
甲跑第一棒的安排方法为种,
乙跑最后一棒的安排方法为种,
甲跑第一棒且乙跑最后一棒的安排方法为种,
甲不能跑第一棒,乙不能跑最后一棒的安排方法为种.
17.(1)(2)当时,的单调递增区间为,无单调递减区间;
当时,的单调递增区间为,单调递减区间为.
【详解】(1),
因为,所以.
(2)函数的定义域为.
,
当时,恒成立,
所以的单调递增区间为,无单调递减区间;
当时,令解得,
的解集为,
的解集为,
所以的单调递增区间为,单调递减区间为.
综上所述:当时,的单调递增区间为,无单调递减区间;
当时,的单调递增区间为,单调递减区间为.
18.(1)(2)的极大值为极小值为(3)
【详解】(1)由题得:,
结合题意可得,
解得,经检验符合题意,
故,,
所以在点处的切线方程为.
(2)由(1)知.
令,解得或,
令,解得,
故在,上单调递增,在上单调递减,
所以的极大值为,
的极小值为;
(3)在上有极大值,无极小值,
又因为,,所以,
所以要使不等式能成立,则.
所以,
故取值范围是.
19.(1)48,16 (2)
【详解】(1)第一阶段每个小组有4个队,进行单循环赛需安排场比赛.
合计需安排场比赛.
即使所有队同时开始比赛,最多需个场馆.
(2)第二阶段进行淘汰赛,由16支队决出前4强需要场比赛.
剩下前4强,需有2场比赛,
首先决出前2名,再有1场比赛决出冠、亚军,再1场比赛决出第三、第四名.
所以16强共计需要场比赛
同课章节目录
