【五环分层导学-课件】6-2 平均数(2)-北师大版数学八(上)
文档属性
| 名称 | 【五环分层导学-课件】6-2 平均数(2)-北师大版数学八(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 16:31:40 | ||
图片预览





文档简介
(共13张PPT)
第六章 数据的分析
第2课 平均数(2)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
算术平均数 加权平均数
%//一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为.//% %//一般地,对于n个数x1,x2…,xn,f1,f2,…,fn分别为各个数所占的比例,我们把x=叫做这n个数的加权平均数,其中f1,f2,…,fn叫做各个数的权.//%
%//一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为.//% %//一般地,对于n个数x1,x2…,xn,f1,f2,…,fn分别为各个数所占的比例,我们把x=叫做这n个数的加权平均数,其中f1,f2,…,fn叫做各个数的权.//%
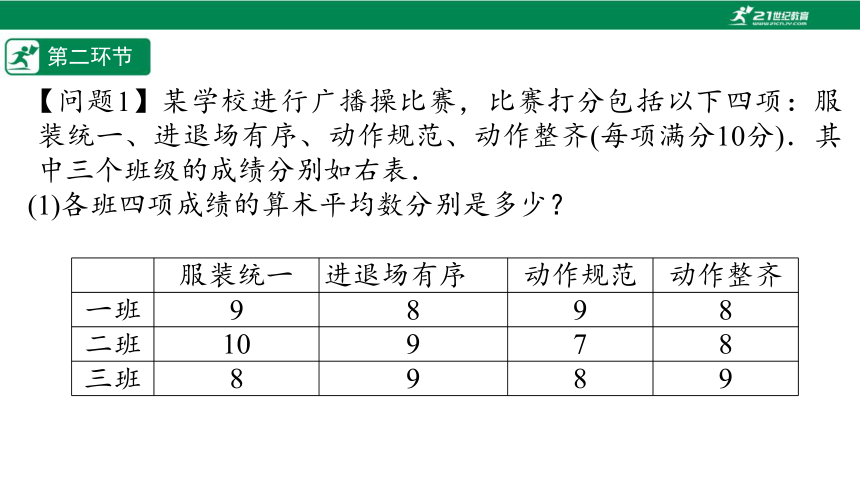
【问题1】某学校进行广播操比赛,比赛打分包括以下四项:服装统一、进退场有序、动作规范、动作整齐(每项满分10分).其中三个班级的成绩分别如右表.
(1)各班四项成绩的算术平均数分别是多少?
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
解:一班的算术平均数是:=8.5(分),
二班的算术平均数是:=8.5(分),
三班的算术平均数是:=8.5(分).
(2)若将服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%、20%、30%、40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
解:9×10%+8×20%+9×30%+8×40%=8.4(分),
10×10%+9×20%+7×30%+8×40%=8.1(分),
8×10%+9×20%+8×30%+9×40%=8.6(分),
∵8.1<8.4<8.6,
∴三班的成绩最高.
(3)你认为上述四项中,哪一项更为重要?按自己的想法设计一个评分方案,并确定哪一个班的广播操比赛成绩最高,与同伴进行交流.
解:我认为“动作整齐”这一项更为重要.
方案:比如服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%、20%、20%、50%的
比例计算各班的广播操比赛成绩.
9×10%+8×20%+9×20%+8×50%=8.3(分),
10×10%+9×20%+7×20%+8×50%=8.2(分),
8×10%+9×20%+8×20%+9×50%=8.7(分),
∵8.2<8.3<8.7,∴三班的成绩最高.
注:其他合理方案均可.
【问题2】你能举出更多生活中加权平均数的实例吗?并说说加权平均数的数据对生活的用处?并与同伴交流.
解:小颖家去年的饮食支出为10000元,教育支出3000元,其他支出为12000元,小颖家今年的这三项支出依此比去年增长了9%,30%,6%.小颖家今年的总支出比去年增长的百分数是多少?这里由于小颖家去年的饮食、教育和其他三项支出金额不等,因此饮食、教育和其他三项支出的增长率“地位”不同,它们对总支出增长率的“影响”不同.不能简单地用算术平均数计算总支出的增长率,而应将这三项支出金额10000元、3000元、12000元分别视为三项支出增长率的“权”,从而总支出的增长率为=10.08%.
1.为全力抗击“新冠肺炎”疫情,响应政府“停课不停学”号召,遵义市教育局发布关于疫情防控期间开展在线教育教学的通知:从2月10日开始,全市九年级按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师2月10日在线答疑问题总个数如表所示:
则2月10日该中学九年级七科老师在线答疑问题总个数的平均数是(%////%)
A.22 B.24 C.25 D.26
学科 语文 数学 英语 物理 化学 道法 历史
数量/个 26 28 28 26 24 21 22
C
2.某公司欲招收职员一名,从学历、经验和工作态度等三个方面对甲乙丙三名应聘者进行了初步测试,测试成绩如下表:
(1)如果将学历、经验和工作态度三项得分按1∶2∶2的比例确定个人的最终得分,并以此为依据确定录用者,那么谁将被录用?
(2)自己确定学历、经验和工作态度三项的权,并根据自己的方案确定录用者.
应聘者 项目 甲 乙 丙
学历 7 7 8
经验 8 7 7
工作态度 6 8 5
解:(1)甲的综合成绩为7×+8×+6×7分,
乙的综合成绩为7×+7×+8×7.4分,
丙的综合成绩为8×+7×+5×6.4分,
则应录用乙;
(2)x甲=(7+8+6)÷3=7,
x乙=(7+7+8)÷3,
x丙=(8+7+5)÷3.
则乙将被录用.
3.(★)某校要从小红、小明和小亮三名同学中挑选一名同学参加数学素养大赛,在最近的四次专题测试中,他们三人的成绩如下表所示:
(1)请算出小红的平均分为多少?
(2)该校根据四次专题考试成绩的重要程度不同而赋予每个专题成绩一个权重,权重比依次为x∶1∶2∶1,最后得出三人的成绩(加权平均数),若从高分到低分排序为小亮、小明、小红,求正整数x的值.
学生专题 集合证明 PISA问题 应用题 动点问题
小红 70 75 80 85
小明 80 80 72 76
小亮 75 75 90 65
解:(1)(70+75+80+85)÷4=77.5分,
答:小红的平均分为77.5分.
(2)由题意得:
,
且,
解得:2<x<4,
∵x为正整数的值,∴x=3,
答:正整数x的值为3.
第六章 数据的分析
第2课 平均数(2)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
算术平均数 加权平均数
%//一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为.//% %//一般地,对于n个数x1,x2…,xn,f1,f2,…,fn分别为各个数所占的比例,我们把x=叫做这n个数的加权平均数,其中f1,f2,…,fn叫做各个数的权.//%
%//一般地,对于n个数x1,x2,…,xn,我们把(x1+x2+…+xn)叫做这n个数的算术平均数,简称平均数,记为.//% %//一般地,对于n个数x1,x2…,xn,f1,f2,…,fn分别为各个数所占的比例,我们把x=叫做这n个数的加权平均数,其中f1,f2,…,fn叫做各个数的权.//%
【问题1】某学校进行广播操比赛,比赛打分包括以下四项:服装统一、进退场有序、动作规范、动作整齐(每项满分10分).其中三个班级的成绩分别如右表.
(1)各班四项成绩的算术平均数分别是多少?
服装统一 进退场有序 动作规范 动作整齐
一班 9 8 9 8
二班 10 9 7 8
三班 8 9 8 9
解:一班的算术平均数是:=8.5(分),
二班的算术平均数是:=8.5(分),
三班的算术平均数是:=8.5(分).
(2)若将服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%、20%、30%、40%的比例计算各班的广播操比赛成绩,那么哪个班的成绩最高?
解:9×10%+8×20%+9×30%+8×40%=8.4(分),
10×10%+9×20%+7×30%+8×40%=8.1(分),
8×10%+9×20%+8×30%+9×40%=8.6(分),
∵8.1<8.4<8.6,
∴三班的成绩最高.
(3)你认为上述四项中,哪一项更为重要?按自己的想法设计一个评分方案,并确定哪一个班的广播操比赛成绩最高,与同伴进行交流.
解:我认为“动作整齐”这一项更为重要.
方案:比如服装统一、进退场有序、动作规范、动作整齐这四项得分依次按10%、20%、20%、50%的
比例计算各班的广播操比赛成绩.
9×10%+8×20%+9×20%+8×50%=8.3(分),
10×10%+9×20%+7×20%+8×50%=8.2(分),
8×10%+9×20%+8×20%+9×50%=8.7(分),
∵8.2<8.3<8.7,∴三班的成绩最高.
注:其他合理方案均可.
【问题2】你能举出更多生活中加权平均数的实例吗?并说说加权平均数的数据对生活的用处?并与同伴交流.
解:小颖家去年的饮食支出为10000元,教育支出3000元,其他支出为12000元,小颖家今年的这三项支出依此比去年增长了9%,30%,6%.小颖家今年的总支出比去年增长的百分数是多少?这里由于小颖家去年的饮食、教育和其他三项支出金额不等,因此饮食、教育和其他三项支出的增长率“地位”不同,它们对总支出增长率的“影响”不同.不能简单地用算术平均数计算总支出的增长率,而应将这三项支出金额10000元、3000元、12000元分别视为三项支出增长率的“权”,从而总支出的增长率为=10.08%.
1.为全力抗击“新冠肺炎”疫情,响应政府“停课不停学”号召,遵义市教育局发布关于疫情防控期间开展在线教育教学的通知:从2月10日开始,全市九年级按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师2月10日在线答疑问题总个数如表所示:
则2月10日该中学九年级七科老师在线答疑问题总个数的平均数是(%////%)
A.22 B.24 C.25 D.26
学科 语文 数学 英语 物理 化学 道法 历史
数量/个 26 28 28 26 24 21 22
C
2.某公司欲招收职员一名,从学历、经验和工作态度等三个方面对甲乙丙三名应聘者进行了初步测试,测试成绩如下表:
(1)如果将学历、经验和工作态度三项得分按1∶2∶2的比例确定个人的最终得分,并以此为依据确定录用者,那么谁将被录用?
(2)自己确定学历、经验和工作态度三项的权,并根据自己的方案确定录用者.
应聘者 项目 甲 乙 丙
学历 7 7 8
经验 8 7 7
工作态度 6 8 5
解:(1)甲的综合成绩为7×+8×+6×7分,
乙的综合成绩为7×+7×+8×7.4分,
丙的综合成绩为8×+7×+5×6.4分,
则应录用乙;
(2)x甲=(7+8+6)÷3=7,
x乙=(7+7+8)÷3,
x丙=(8+7+5)÷3.
则乙将被录用.
3.(★)某校要从小红、小明和小亮三名同学中挑选一名同学参加数学素养大赛,在最近的四次专题测试中,他们三人的成绩如下表所示:
(1)请算出小红的平均分为多少?
(2)该校根据四次专题考试成绩的重要程度不同而赋予每个专题成绩一个权重,权重比依次为x∶1∶2∶1,最后得出三人的成绩(加权平均数),若从高分到低分排序为小亮、小明、小红,求正整数x的值.
学生专题 集合证明 PISA问题 应用题 动点问题
小红 70 75 80 85
小明 80 80 72 76
小亮 75 75 90 65
解:(1)(70+75+80+85)÷4=77.5分,
答:小红的平均分为77.5分.
(2)由题意得:
,
且,
解得:2<x<4,
∵x为正整数的值,∴x=3,
答:正整数x的值为3.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
