第七章 平面直角坐标系练习卷(基础篇)(含解析)
文档属性
| 名称 | 第七章 平面直角坐标系练习卷(基础篇)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 20:46:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
(基础篇)2023-2024学年下学期初中数学人教版七年级第7章练习卷
一.选择题(共4小题)
1.点P(2,﹣)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,﹣1) C.(﹣3,1) D.(1,﹣2)
3.已知点A(a,b),其中a,b均为实数,若a,b满足3a=2b+5,则称点A为“和谐点”.若点 是“和谐点”,则点B在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,点A,B,C都在方格纸的格点上,若点A的坐标为(0,1),点B的坐标为(2,﹣1),则点C的坐标是( )
A.(1,0) B.(2,0) C.(1,1) D.(2,1)
二.填空题(共4小题)
5.点P(﹣3,4)到y轴的距离是 .
6.若点P(m+1,m﹣3)在平面直角坐标系二、四象限角平分线上,则点P的坐标为 .
7.如图,在“笑脸”的“嘴巴”上找一格点,这一格点的坐标可以为 (写出一点即可).
8.在平面直角坐标系中,已知点M(m﹣1,2m+4)在x轴上,则点M的坐标为 .
三.解答题(共2小题)
9.已知平面直角坐标系中一点P(m+1,2m﹣4),根据下列条件,求点P的坐标.
(1)若直线PQ与y轴平行,且点Q的坐标为(﹣3,2);
(2)若点P到x轴,y轴的距离相等.
10.在平面直角坐标系中,△ABC经过平移得到△AB′C′,△ABC与△ACB′C′的位置如图所示.
(1)分别写出点B,B′的坐标;
(2)请结合平移的相关知识说明△A′B′C′可由△ABC经过怎样的平移得到?
(3)点M(a+2,b﹣1)为△ABC内一点,其平移后的对应点为M′(9﹣b,2a+11),求实数a,b的值.
(基础篇)2023-2024学年下学期初中数学人教版七年级第7章练习卷
参考答案与试题解析
一.选择题(共4小题)
1.点P(2,﹣)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:由于2>0,﹣<0,
∴点P(2,﹣)在平面直角坐标系的第四象限.
故选:D.
2.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,﹣1) C.(﹣3,1) D.(1,﹣2)
【解答】解:如图,
“兵”位于点(﹣3,1).
故选:C.
3.已知点A(a,b),其中a,b均为实数,若a,b满足3a=2b+5,则称点A为“和谐点”.若点 是“和谐点”,则点B在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵点 是“和谐点”,
∴3(k+2)=2(1﹣)+5,
解得k=,
∴k+2=,1﹣k=,
∴点B在第一象限.
故选:A.
4.如图,点A,B,C都在方格纸的格点上,若点A的坐标为(0,1),点B的坐标为(2,﹣1),则点C的坐标是( )
A.(1,0) B.(2,0) C.(1,1) D.(2,1)
【解答】解:如图所示:
点C的坐标为(2,0).
故选:B.
二.填空题(共4小题)
5.点P(﹣3,4)到y轴的距离是 3 .
【解答】解:点P(﹣3,4)到y轴的距离是|﹣3|=3,
故答案为:3.
6.若点P(m+1,m﹣3)在平面直角坐标系二、四象限角平分线上,则点P的坐标为 (2,﹣2) .
【解答】解:∵点P(m+1,m﹣3)在第二、四象限的角平分线上,
∴m+1+m﹣3=0,
解得m=1,
∴P(2,﹣2).
故答案为:(2,﹣2).
7.如图,在“笑脸”的“嘴巴”上找一格点,这一格点的坐标可以为 (0,﹣2)(答案不唯一) (写出一点即可).
【解答】解:如图,在“笑脸”的“嘴巴”上找一格点,这一格点的坐标可以为(0,﹣2),(1,﹣2),(2,﹣1),(﹣2,﹣1),(﹣1,﹣2)等.
故答案为:(0,﹣2)(答案不唯一).
8.在平面直角坐标系中,已知点M(m﹣1,2m+4)在x轴上,则点M的坐标为 (﹣3,0) .
【解答】解:由题意得,2m+4=0,解得m=﹣2,
∴m﹣1=﹣3,
∴M(﹣3,0),
故答案为:(﹣3,0).
三.解答题(共2小题)
9.已知平面直角坐标系中一点P(m+1,2m﹣4),根据下列条件,求点P的坐标.
(1)若直线PQ与y轴平行,且点Q的坐标为(﹣3,2);
(2)若点P到x轴,y轴的距离相等.
【解答】解:(1)∵点Q(﹣3,2),且直线PQ与y轴平行,点P(m+1,2m﹣4),
∴m+1=﹣3,
解得m=﹣4,
∴2m﹣4=﹣8﹣4=﹣12,
∴P(﹣3,﹣12);
(2)∵点P到轴,y轴的距离相等,
∴=,
即m+1=2m﹣4或m+1=4﹣2m,
解得m=5或m=1,
∴m+1=5+1=6或m+1=1+1=2,
2m﹣4=10﹣4=6或2m﹣4=2﹣4=﹣2,
∴P(6,6)或P(2,﹣2).
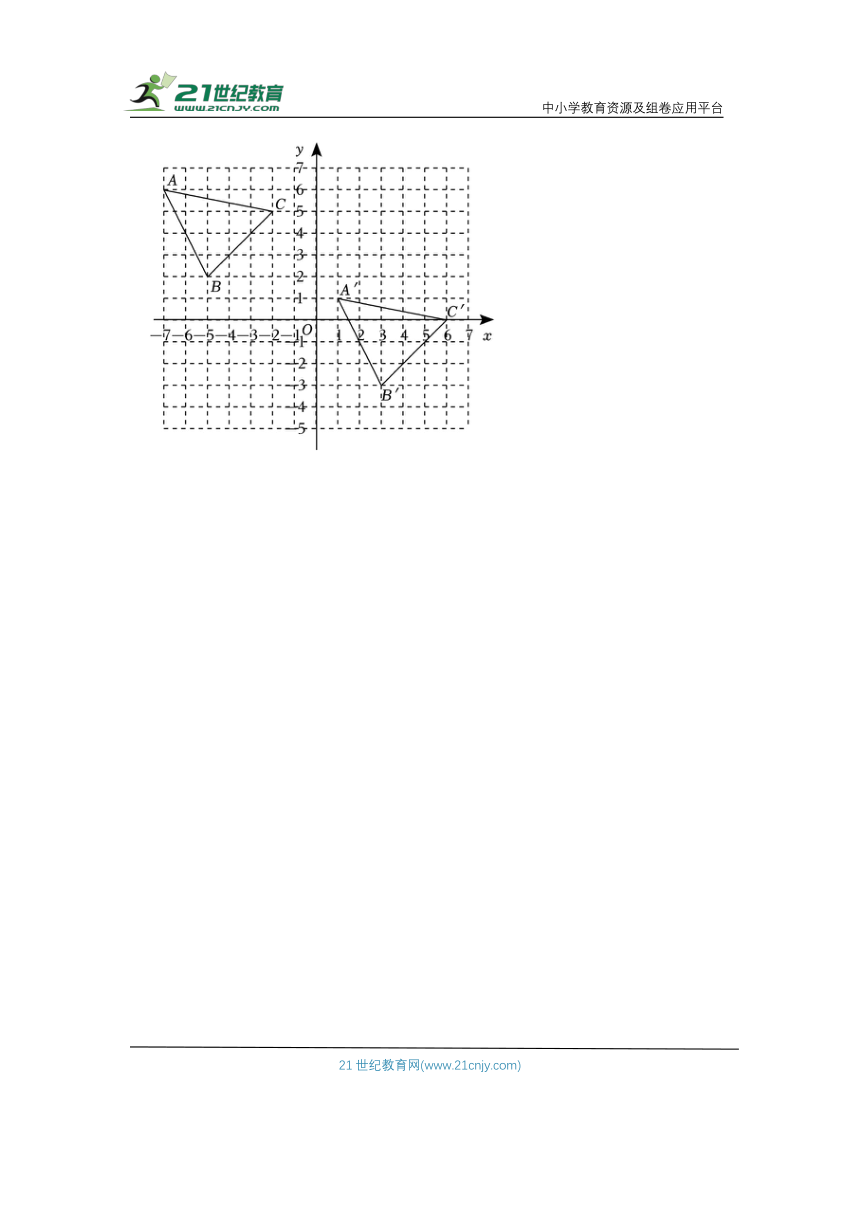
10.在平面直角坐标系中,△ABC经过平移得到△AB′C′,△ABC与△ACB′C′的位置如图所示.
(1)分别写出点B,B′的坐标;
(2)请结合平移的相关知识说明△A′B′C′可由△ABC经过怎样的平移得到?
(3)点M(a+2,b﹣1)为△ABC内一点,其平移后的对应点为M′(9﹣b,2a+11),求实数a,b的值.
【解答】解:(1)点B的坐标为(﹣5,2),点B'的坐标为(3,﹣3),
(2)△A'B'C'可由△ABC向右平移8个长度单位,再向下平移5个长度单位得到;
(3)∵点M(a+2,b﹣1)和点M'(9﹣b,2a+11)是对应点,
∴,解得:.
∴a=﹣6,b=5.
21世纪教育网(www.21cnjy.com)
(基础篇)2023-2024学年下学期初中数学人教版七年级第7章练习卷
一.选择题(共4小题)
1.点P(2,﹣)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,﹣1) C.(﹣3,1) D.(1,﹣2)
3.已知点A(a,b),其中a,b均为实数,若a,b满足3a=2b+5,则称点A为“和谐点”.若点 是“和谐点”,则点B在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,点A,B,C都在方格纸的格点上,若点A的坐标为(0,1),点B的坐标为(2,﹣1),则点C的坐标是( )
A.(1,0) B.(2,0) C.(1,1) D.(2,1)
二.填空题(共4小题)
5.点P(﹣3,4)到y轴的距离是 .
6.若点P(m+1,m﹣3)在平面直角坐标系二、四象限角平分线上,则点P的坐标为 .
7.如图,在“笑脸”的“嘴巴”上找一格点,这一格点的坐标可以为 (写出一点即可).
8.在平面直角坐标系中,已知点M(m﹣1,2m+4)在x轴上,则点M的坐标为 .
三.解答题(共2小题)
9.已知平面直角坐标系中一点P(m+1,2m﹣4),根据下列条件,求点P的坐标.
(1)若直线PQ与y轴平行,且点Q的坐标为(﹣3,2);
(2)若点P到x轴,y轴的距离相等.
10.在平面直角坐标系中,△ABC经过平移得到△AB′C′,△ABC与△ACB′C′的位置如图所示.
(1)分别写出点B,B′的坐标;
(2)请结合平移的相关知识说明△A′B′C′可由△ABC经过怎样的平移得到?
(3)点M(a+2,b﹣1)为△ABC内一点,其平移后的对应点为M′(9﹣b,2a+11),求实数a,b的值.
(基础篇)2023-2024学年下学期初中数学人教版七年级第7章练习卷
参考答案与试题解析
一.选择题(共4小题)
1.点P(2,﹣)在平面直角坐标系的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:由于2>0,﹣<0,
∴点P(2,﹣)在平面直角坐标系的第四象限.
故选:D.
2.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1) B.(﹣2,﹣1) C.(﹣3,1) D.(1,﹣2)
【解答】解:如图,
“兵”位于点(﹣3,1).
故选:C.
3.已知点A(a,b),其中a,b均为实数,若a,b满足3a=2b+5,则称点A为“和谐点”.若点 是“和谐点”,则点B在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵点 是“和谐点”,
∴3(k+2)=2(1﹣)+5,
解得k=,
∴k+2=,1﹣k=,
∴点B在第一象限.
故选:A.
4.如图,点A,B,C都在方格纸的格点上,若点A的坐标为(0,1),点B的坐标为(2,﹣1),则点C的坐标是( )
A.(1,0) B.(2,0) C.(1,1) D.(2,1)
【解答】解:如图所示:
点C的坐标为(2,0).
故选:B.
二.填空题(共4小题)
5.点P(﹣3,4)到y轴的距离是 3 .
【解答】解:点P(﹣3,4)到y轴的距离是|﹣3|=3,
故答案为:3.
6.若点P(m+1,m﹣3)在平面直角坐标系二、四象限角平分线上,则点P的坐标为 (2,﹣2) .
【解答】解:∵点P(m+1,m﹣3)在第二、四象限的角平分线上,
∴m+1+m﹣3=0,
解得m=1,
∴P(2,﹣2).
故答案为:(2,﹣2).
7.如图,在“笑脸”的“嘴巴”上找一格点,这一格点的坐标可以为 (0,﹣2)(答案不唯一) (写出一点即可).
【解答】解:如图,在“笑脸”的“嘴巴”上找一格点,这一格点的坐标可以为(0,﹣2),(1,﹣2),(2,﹣1),(﹣2,﹣1),(﹣1,﹣2)等.
故答案为:(0,﹣2)(答案不唯一).
8.在平面直角坐标系中,已知点M(m﹣1,2m+4)在x轴上,则点M的坐标为 (﹣3,0) .
【解答】解:由题意得,2m+4=0,解得m=﹣2,
∴m﹣1=﹣3,
∴M(﹣3,0),
故答案为:(﹣3,0).
三.解答题(共2小题)
9.已知平面直角坐标系中一点P(m+1,2m﹣4),根据下列条件,求点P的坐标.
(1)若直线PQ与y轴平行,且点Q的坐标为(﹣3,2);
(2)若点P到x轴,y轴的距离相等.
【解答】解:(1)∵点Q(﹣3,2),且直线PQ与y轴平行,点P(m+1,2m﹣4),
∴m+1=﹣3,
解得m=﹣4,
∴2m﹣4=﹣8﹣4=﹣12,
∴P(﹣3,﹣12);
(2)∵点P到轴,y轴的距离相等,
∴=,
即m+1=2m﹣4或m+1=4﹣2m,
解得m=5或m=1,
∴m+1=5+1=6或m+1=1+1=2,
2m﹣4=10﹣4=6或2m﹣4=2﹣4=﹣2,
∴P(6,6)或P(2,﹣2).
10.在平面直角坐标系中,△ABC经过平移得到△AB′C′,△ABC与△ACB′C′的位置如图所示.
(1)分别写出点B,B′的坐标;
(2)请结合平移的相关知识说明△A′B′C′可由△ABC经过怎样的平移得到?
(3)点M(a+2,b﹣1)为△ABC内一点,其平移后的对应点为M′(9﹣b,2a+11),求实数a,b的值.
【解答】解:(1)点B的坐标为(﹣5,2),点B'的坐标为(3,﹣3),
(2)△A'B'C'可由△ABC向右平移8个长度单位,再向下平移5个长度单位得到;
(3)∵点M(a+2,b﹣1)和点M'(9﹣b,2a+11)是对应点,
∴,解得:.
∴a=﹣6,b=5.
21世纪教育网(www.21cnjy.com)
