【五环分层导学-课件】4-7 一次函数图像的应用(2)-北师大版数学八(上)
文档属性
| 名称 | 【五环分层导学-课件】4-7 一次函数图像的应用(2)-北师大版数学八(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第四章 一次函数
第7课 一次函数图像的应用(2)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)从“数”的角度,要确定一次函数表达式y=kx+b(k≠0)需要确定两个常数%////%、%////%,从“形”的角度,一次函数是一条直线,需要确定%////%点.
(2)用待定系数法确定一次函数的表达式的步骤:
① 设——设出一次函数表达式,即%// //% ;
② 代——把已知条件代入y=kx+b中,得到关于%// //%的方程(组);
③ 解——解方程(组),求%// //%;
④ 写——写出%// //%表达式.
k
b
两
y=kx+b(k≠0)
k,b
k,b
一次函数
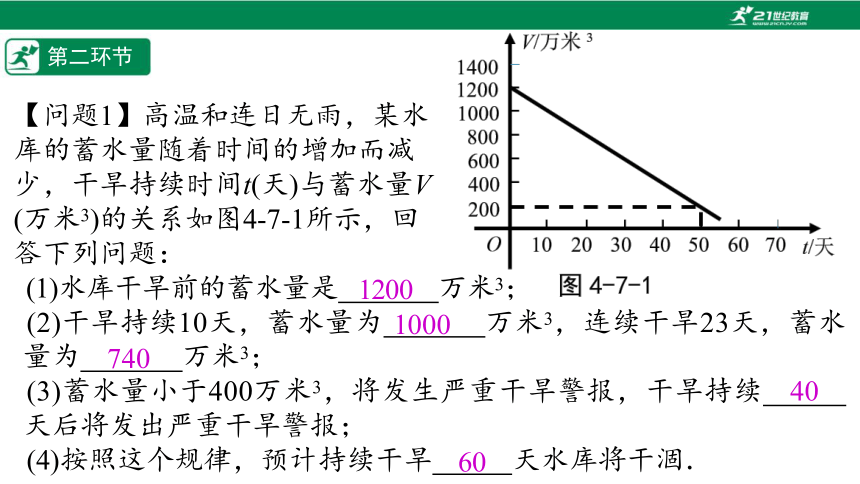
【问题1】高温和连日无雨,某水
库的蓄水量随着时间的增加而减
少,干旱持续时间t(天)与蓄水量V
(万米3)的关系如图4-7-1所示,回
答下列问题:
(1)水库干旱前的蓄水量是%// //%万米3;
(2)干旱持续10天,蓄水量为%// //%万米3,连续干旱23天,蓄水量为%// //%万米3;
(3)蓄水量小于400万米3,将发生严重干旱警报,干旱持续%////%天后将发出严重干旱警报;
(4)按照这个规律,预计持续干旱%////%天水库将干涸.
1200
1000
740
40
60
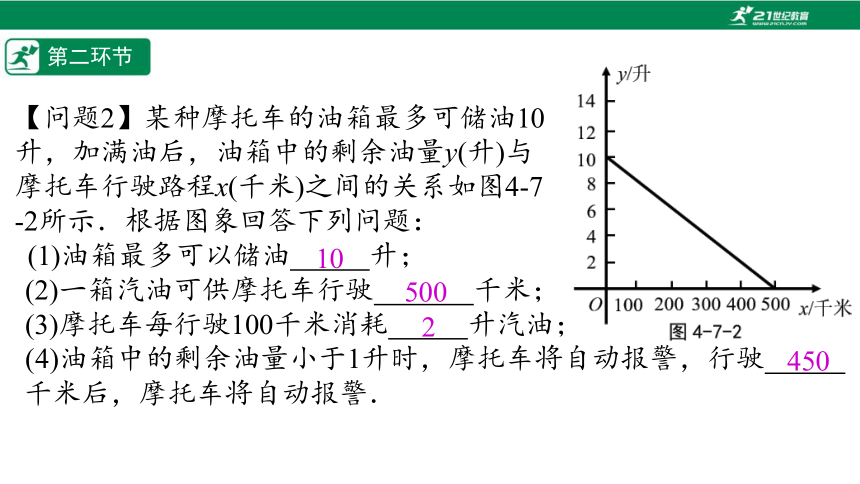
【问题2】某种摩托车的油箱最多可储油10
升,加满油后,油箱中的剩余油量y(升)与
摩托车行驶路程x(千米)之间的关系如图4-7
-2所示.根据图象回答下列问题:
(1)油箱最多可以储油%////%升;
(2)一箱汽油可供摩托车行驶%// //%千米;
(3)摩托车每行驶100千米消耗%////%升汽油;
(4)油箱中的剩余油量小于1升时,摩托车将自动报警,行驶%////%千米后,摩托车将自动报警.
10
500
2
450
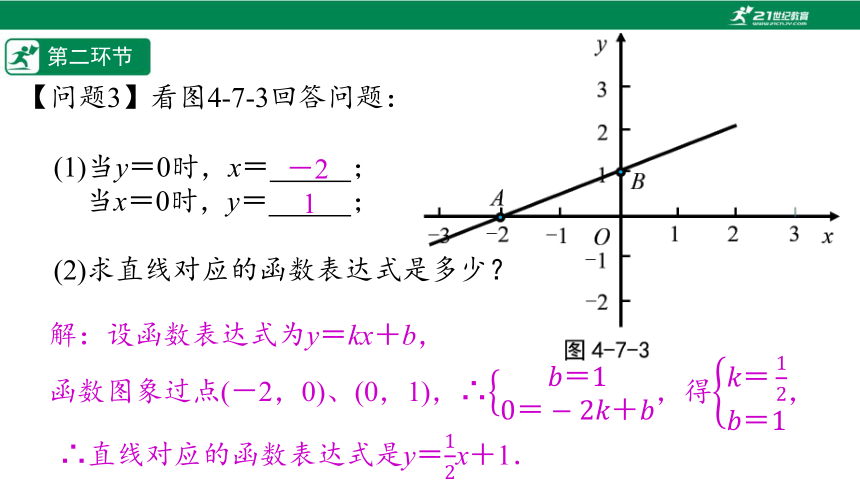
【问题3】看图4-7-3回答问题:
(1)当y=0时,x=%// //%;
当x=0时,y=%// //%;
(2)求直线对应的函数表达式是多少?
解:设函数表达式为y=kx+b,
函数图象过点(-2,0)、(0,1),∴,得,
∴直线对应的函数表达式是y=x+1.
-2
1
(3)一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
(4)一次函数y=kx+b(k≠0)与方程kx+b-y=0有什么关系?
解:一元一次方程0.5x+1=0的解是一次函数y=0.5x+1与x轴的交点的横坐标.
小结:
一元一次方程kx+b=0(k≠0)的解是一次函数y=kx+b与x轴交点的横坐标.
1.为了提高某种农作物的产量,农场通常采用喷施药物的方法控制其高度.已知该农作物的平均高度y(米)与每公顷所喷施药物的质量
x(千克/公顷)之间的关
系如图4-7-4所示,经
验表明,该种农作物
高度在1.25米左右时,
它的产量最高,那么
每公顷应喷施药物
%////%千克.
2.5
2.方程y=kx+b(k≠0)与x轴的交点是(-3,0),
则kx+b-y=0的一个解为%// //%;
方程y-kx+b=0的一个解为x=3,y=4,
则函数y=kx-b(k≠0)必经过点%// //%.
x=-3
(3,4)
3.如图4-7-5,某植物t天后的高度为y cm,l反映了y与t之间的关系,根据图象回答下列问题:
(1)3天后该植物高度为多少?
(2)预测该植物12天后的高度;
(3)几天后该植物的高度为10 cm?
(4)图象对应的一次函数y=kt+b中,
k和b的实际意义分别是什么?
解:(1)设y=kt+b,把(0,3),(6,8)代入y=kt+b,
∴,解得,
∴y=t+3,
当t=3时,y=×3+3=5.5,
答:3天后该植物高度为5.5 cm.
(2)当t=12时,y=×12+3=13(cm),
答:预测该植物12天后的高度为13 cm.
(3)当y=10时,t+3=10,解得:t=8.4(天),
答:8.4天后该植物的高度为10 cm.
(4)k表示植物生长速度,b表示植物原先的高度.
4.(★)某汽车离开某城市的距离y(km)与行驶时间t( h)之间的关系式为y=kt+30,其图象如图4-7-6所示.
(1)在1 h至3 h之间,汽车行驶的路程是多少?
(2)你能确定k的值吗?这里k的具体含义是什么?
解:(1)根据函数图象可知:t=1时,y=90.
将t=1,y=90代入得:k+30=90.
解得;k=60.
所以函数的关系式为y=60t+30.
将t=3代入得:y=210.
∴在1 h至3 h之间,汽车行驶的路程=210-90=120 km;
(2)由(1)可知:k=60,k的具体含义是汽车的行驶速度.
第四章 一次函数
第7课 一次函数图像的应用(2)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)从“数”的角度,要确定一次函数表达式y=kx+b(k≠0)需要确定两个常数%////%、%////%,从“形”的角度,一次函数是一条直线,需要确定%////%点.
(2)用待定系数法确定一次函数的表达式的步骤:
① 设——设出一次函数表达式,即%// //% ;
② 代——把已知条件代入y=kx+b中,得到关于%// //%的方程(组);
③ 解——解方程(组),求%// //%;
④ 写——写出%// //%表达式.
k
b
两
y=kx+b(k≠0)
k,b
k,b
一次函数
【问题1】高温和连日无雨,某水
库的蓄水量随着时间的增加而减
少,干旱持续时间t(天)与蓄水量V
(万米3)的关系如图4-7-1所示,回
答下列问题:
(1)水库干旱前的蓄水量是%// //%万米3;
(2)干旱持续10天,蓄水量为%// //%万米3,连续干旱23天,蓄水量为%// //%万米3;
(3)蓄水量小于400万米3,将发生严重干旱警报,干旱持续%////%天后将发出严重干旱警报;
(4)按照这个规律,预计持续干旱%////%天水库将干涸.
1200
1000
740
40
60
【问题2】某种摩托车的油箱最多可储油10
升,加满油后,油箱中的剩余油量y(升)与
摩托车行驶路程x(千米)之间的关系如图4-7
-2所示.根据图象回答下列问题:
(1)油箱最多可以储油%////%升;
(2)一箱汽油可供摩托车行驶%// //%千米;
(3)摩托车每行驶100千米消耗%////%升汽油;
(4)油箱中的剩余油量小于1升时,摩托车将自动报警,行驶%////%千米后,摩托车将自动报警.
10
500
2
450
【问题3】看图4-7-3回答问题:
(1)当y=0时,x=%// //%;
当x=0时,y=%// //%;
(2)求直线对应的函数表达式是多少?
解:设函数表达式为y=kx+b,
函数图象过点(-2,0)、(0,1),∴,得,
∴直线对应的函数表达式是y=x+1.
-2
1
(3)一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
(4)一次函数y=kx+b(k≠0)与方程kx+b-y=0有什么关系?
解:一元一次方程0.5x+1=0的解是一次函数y=0.5x+1与x轴的交点的横坐标.
小结:
一元一次方程kx+b=0(k≠0)的解是一次函数y=kx+b与x轴交点的横坐标.
1.为了提高某种农作物的产量,农场通常采用喷施药物的方法控制其高度.已知该农作物的平均高度y(米)与每公顷所喷施药物的质量
x(千克/公顷)之间的关
系如图4-7-4所示,经
验表明,该种农作物
高度在1.25米左右时,
它的产量最高,那么
每公顷应喷施药物
%////%千克.
2.5
2.方程y=kx+b(k≠0)与x轴的交点是(-3,0),
则kx+b-y=0的一个解为%// //%;
方程y-kx+b=0的一个解为x=3,y=4,
则函数y=kx-b(k≠0)必经过点%// //%.
x=-3
(3,4)
3.如图4-7-5,某植物t天后的高度为y cm,l反映了y与t之间的关系,根据图象回答下列问题:
(1)3天后该植物高度为多少?
(2)预测该植物12天后的高度;
(3)几天后该植物的高度为10 cm?
(4)图象对应的一次函数y=kt+b中,
k和b的实际意义分别是什么?
解:(1)设y=kt+b,把(0,3),(6,8)代入y=kt+b,
∴,解得,
∴y=t+3,
当t=3时,y=×3+3=5.5,
答:3天后该植物高度为5.5 cm.
(2)当t=12时,y=×12+3=13(cm),
答:预测该植物12天后的高度为13 cm.
(3)当y=10时,t+3=10,解得:t=8.4(天),
答:8.4天后该植物的高度为10 cm.
(4)k表示植物生长速度,b表示植物原先的高度.
4.(★)某汽车离开某城市的距离y(km)与行驶时间t( h)之间的关系式为y=kt+30,其图象如图4-7-6所示.
(1)在1 h至3 h之间,汽车行驶的路程是多少?
(2)你能确定k的值吗?这里k的具体含义是什么?
解:(1)根据函数图象可知:t=1时,y=90.
将t=1,y=90代入得:k+30=90.
解得;k=60.
所以函数的关系式为y=60t+30.
将t=3代入得:y=210.
∴在1 h至3 h之间,汽车行驶的路程=210-90=120 km;
(2)由(1)可知:k=60,k的具体含义是汽车的行驶速度.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
