【五环分层导学-课件】4-8 一次函数图象的应用(3)-北师大版数学八(上)
文档属性
| 名称 | 【五环分层导学-课件】4-8 一次函数图象的应用(3)-北师大版数学八(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第四章 一次函数
第8课 一次函数图像的应用(3)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
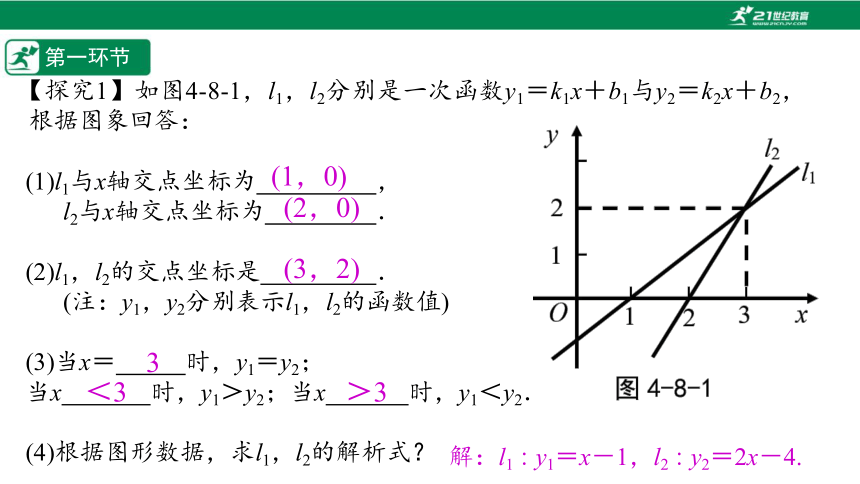
【探究1】如图4-8-1,l1,l2分别是一次函数y1=k1x+b1与y2=k2x+b2,根据图象回答:
(1)l1与x轴交点坐标为%// //%,
l2与x轴交点坐标为%// //%.
(2)l1,l2的交点坐标是%// //%.
(注:y1,y2分别表示l1,l2的函数值)
(3)当x=%////%时,y1=y2;
当x%// //%时,y1>y2;当x%// //%时,y1<y2.
(4)根据图形数据,求l1,l2的解析式?
解:l1∶y1=x-1,l2∶y2=2x-4.//
(1,0)
(2,0)
(3,2)
3
<3
>3
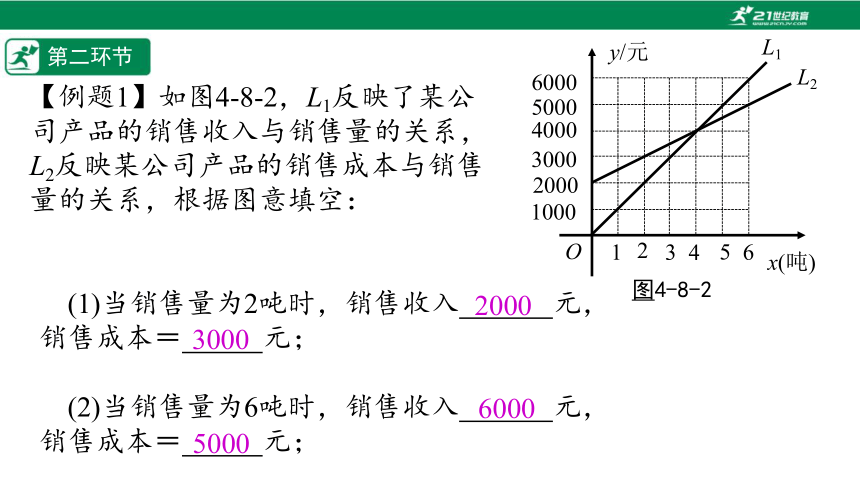
【例题1】如图4-8-2,L1反映了某公
司产品的销售收入与销售量的关系,
L2反映某公司产品的销售成本与销售
量的关系,根据图意填空:
(1)当销售量为2吨时,销售收入%// //%元,销售成本=%// //%元;
(2)当销售量为6吨时,销售收入%// //%元,销售成本=%// //%元;
图4-8-2
y/元
O
x(吨)
6000
2000
4
L1
2
4000
L2
6
5000
3000
1000
1
3
5
2000
3000
6000
5000
(3)当销售量为%////%吨时,销售收入等于销售成本;
(4)当销售量%// //%吨时,该公司赢利(收入大于成本);
当销售量%// //%吨时,该公司亏损(收入小于成本);
(5)求L1,L2的函数表达式是多少?
解:L1的函数表达式是y=1000x,
设L2的函数表达式为y=k2x+b2,
把(0,2000)、(4,4000)代入可得k2=500,b2=2000,
∴L2的函数表达式是y=500x+2000.
4
大于4
小于4
(6)L1与L2对应的两个一次函数y=k1x+b1与y=k2x+b2中,k1,b1,k2,b2的实际意义各是什么?
解:k1的实际意义是销售1吨产品的销售收入,b1的实际意义初始收入为0;
k2的实际意义是每销售1吨的成本,b2的实际意义是未销售时,初始成本为2000元.
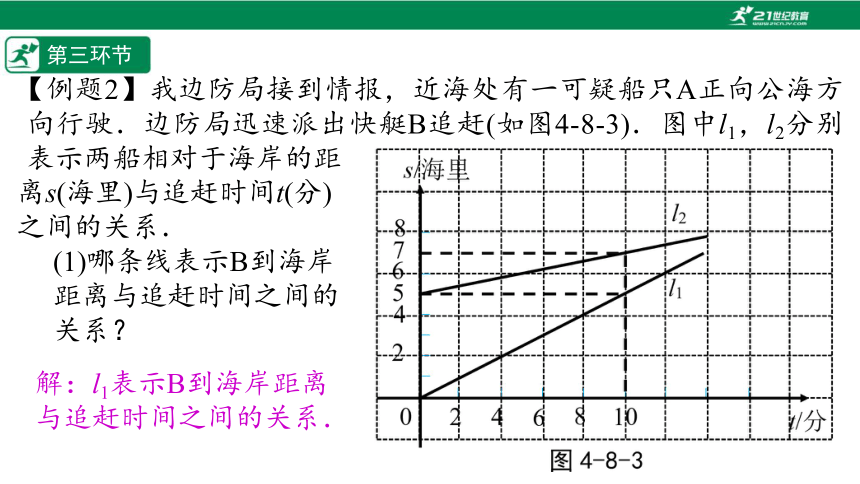
【例题2】我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶(如图4-8-3).图中l1,l2分别表示两船相对于海岸的距
离s(海里)与追赶时间t(分)
之间的关系.
(1)哪条线表示B到海岸
距离与追赶时间之间的
关系?
解:l1表示B到海岸距离与追赶时间之间的关系.
(2)A、B哪个速度快?
(3)15分钟内B能否追上A?
(4)如果一直追下去,那么B能否追上A?
解:B的速度快.A的速度是0.2海里/分;B的速度是0.5海里/分.
解:15分钟时B到海岸的距离7.5海里,
15分钟时A到海岸的距离8海里,
∴15分钟内B不能追上A .
解:如果一直追下去,B能追上A .
(5)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
(6)l1与l2对应的两个一次函数s=k1t+b1与s=k2t+b2,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少?
解:能.设B在x时追上A,可得x=x+5,解得x=,此时A离海岸的距离是海里,它还没有到达公海,
∴照此速度,B能在A逃入公海前将其拦截.
解:k1的实际意义是B的速度,k2的实际意义是A的速度;
A的速度是0.2海里/分,B的速度是0.5海里/分.
1.A,B两地相距80 km,甲、乙两人
沿同一条路从A地到B地.如图,l1,
l2分别表示甲、乙两人离开A地的距
离s(km)与时间t( h)之间的关系.
(1)乙先出发%////% h后,甲才出发;
(2)请分别求出甲、乙的速度;并直接写出l1、l2的表达式.
(3)甲到达B地时,乙距B地还有多远?,乙还需几小时到达B地?
(4)l1和l2的交点坐标是?有什么现实意义?
s(km)
O
t(h)
3
1.5
2
20
40
80
D
C
E
1
F
l1
l2
解:(1)设甲离开A地的距离s(km)与乙出发的时间t( h)的关系式为s=kt+b,
将F(1.5,20)、E(3,80)代入s=kt+b,
,解得:,
∴甲离开A地的距离s(km)与乙出发的时间t( h)的
关系式为:s=40t-40(1≤t≤3).
∴点D的坐标为(1,0),
∴乙先出发1 h后,甲才出发.故答案为:1.
(2)甲的速度为80÷(3-1)=40(km/h),
乙的速度为40÷3(km/h).故答案为:40;.
甲离开A地的距离s(km)与乙出发的时间t( h)的
关系式为:s=40t-40(1≤t≤3).
乙离开A地的距离s(km)与乙出发的时间t( h)的
关系式为st(0<t≤3).
(3)甲到达B地时,乙距B地还有40 km,乙还需3 h到达B地.
(4)(1.5,20),甲出发0.5小时后在离开A地20 km处追上了乙.
2.(★)联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.
(1)分别表示出y1与x,y2与x的函数关系式.
(2)月通话时间为多长时,A、B两种套餐收费一样?
解:(1)A套餐的收费方式:y1=0.1x+15;
B套餐的收费方式:y2=0.15x;
(2)∵A、B两种套餐收费一样,
∴y1=y2,即0.1x+15=0.15x,得到x=300,
答:当月通话时间是300分钟时,A、B两种套餐收费一样.
第四章 一次函数
第8课 一次函数图像的应用(3)
北师大版八年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
【探究1】如图4-8-1,l1,l2分别是一次函数y1=k1x+b1与y2=k2x+b2,根据图象回答:
(1)l1与x轴交点坐标为%// //%,
l2与x轴交点坐标为%// //%.
(2)l1,l2的交点坐标是%// //%.
(注:y1,y2分别表示l1,l2的函数值)
(3)当x=%////%时,y1=y2;
当x%// //%时,y1>y2;当x%// //%时,y1<y2.
(4)根据图形数据,求l1,l2的解析式?
解:l1∶y1=x-1,l2∶y2=2x-4.//
(1,0)
(2,0)
(3,2)
3
<3
>3
【例题1】如图4-8-2,L1反映了某公
司产品的销售收入与销售量的关系,
L2反映某公司产品的销售成本与销售
量的关系,根据图意填空:
(1)当销售量为2吨时,销售收入%// //%元,销售成本=%// //%元;
(2)当销售量为6吨时,销售收入%// //%元,销售成本=%// //%元;
图4-8-2
y/元
O
x(吨)
6000
2000
4
L1
2
4000
L2
6
5000
3000
1000
1
3
5
2000
3000
6000
5000
(3)当销售量为%////%吨时,销售收入等于销售成本;
(4)当销售量%// //%吨时,该公司赢利(收入大于成本);
当销售量%// //%吨时,该公司亏损(收入小于成本);
(5)求L1,L2的函数表达式是多少?
解:L1的函数表达式是y=1000x,
设L2的函数表达式为y=k2x+b2,
把(0,2000)、(4,4000)代入可得k2=500,b2=2000,
∴L2的函数表达式是y=500x+2000.
4
大于4
小于4
(6)L1与L2对应的两个一次函数y=k1x+b1与y=k2x+b2中,k1,b1,k2,b2的实际意义各是什么?
解:k1的实际意义是销售1吨产品的销售收入,b1的实际意义初始收入为0;
k2的实际意义是每销售1吨的成本,b2的实际意义是未销售时,初始成本为2000元.
【例题2】我边防局接到情报,近海处有一可疑船只A正向公海方向行驶.边防局迅速派出快艇B追赶(如图4-8-3).图中l1,l2分别表示两船相对于海岸的距
离s(海里)与追赶时间t(分)
之间的关系.
(1)哪条线表示B到海岸
距离与追赶时间之间的
关系?
解:l1表示B到海岸距离与追赶时间之间的关系.
(2)A、B哪个速度快?
(3)15分钟内B能否追上A?
(4)如果一直追下去,那么B能否追上A?
解:B的速度快.A的速度是0.2海里/分;B的速度是0.5海里/分.
解:15分钟时B到海岸的距离7.5海里,
15分钟时A到海岸的距离8海里,
∴15分钟内B不能追上A .
解:如果一直追下去,B能追上A .
(5)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
(6)l1与l2对应的两个一次函数s=k1t+b1与s=k2t+b2,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少?
解:能.设B在x时追上A,可得x=x+5,解得x=,此时A离海岸的距离是海里,它还没有到达公海,
∴照此速度,B能在A逃入公海前将其拦截.
解:k1的实际意义是B的速度,k2的实际意义是A的速度;
A的速度是0.2海里/分,B的速度是0.5海里/分.
1.A,B两地相距80 km,甲、乙两人
沿同一条路从A地到B地.如图,l1,
l2分别表示甲、乙两人离开A地的距
离s(km)与时间t( h)之间的关系.
(1)乙先出发%////% h后,甲才出发;
(2)请分别求出甲、乙的速度;并直接写出l1、l2的表达式.
(3)甲到达B地时,乙距B地还有多远?,乙还需几小时到达B地?
(4)l1和l2的交点坐标是?有什么现实意义?
s(km)
O
t(h)
3
1.5
2
20
40
80
D
C
E
1
F
l1
l2
解:(1)设甲离开A地的距离s(km)与乙出发的时间t( h)的关系式为s=kt+b,
将F(1.5,20)、E(3,80)代入s=kt+b,
,解得:,
∴甲离开A地的距离s(km)与乙出发的时间t( h)的
关系式为:s=40t-40(1≤t≤3).
∴点D的坐标为(1,0),
∴乙先出发1 h后,甲才出发.故答案为:1.
(2)甲的速度为80÷(3-1)=40(km/h),
乙的速度为40÷3(km/h).故答案为:40;.
甲离开A地的距离s(km)与乙出发的时间t( h)的
关系式为:s=40t-40(1≤t≤3).
乙离开A地的距离s(km)与乙出发的时间t( h)的
关系式为st(0<t≤3).
(3)甲到达B地时,乙距B地还有40 km,乙还需3 h到达B地.
(4)(1.5,20),甲出发0.5小时后在离开A地20 km处追上了乙.
2.(★)联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.
(1)分别表示出y1与x,y2与x的函数关系式.
(2)月通话时间为多长时,A、B两种套餐收费一样?
解:(1)A套餐的收费方式:y1=0.1x+15;
B套餐的收费方式:y2=0.15x;
(2)∵A、B两种套餐收费一样,
∴y1=y2,即0.1x+15=0.15x,得到x=300,
答:当月通话时间是300分钟时,A、B两种套餐收费一样.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
