2024年中考数学二轮复习丢分知识点练习---反比例函数与等腰三角形 学案(无答案)
文档属性
| 名称 | 2024年中考数学二轮复习丢分知识点练习---反比例函数与等腰三角形 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 19:47:27 | ||
图片预览

文档简介
二、反比例函数与等腰三角形
丢分题精析
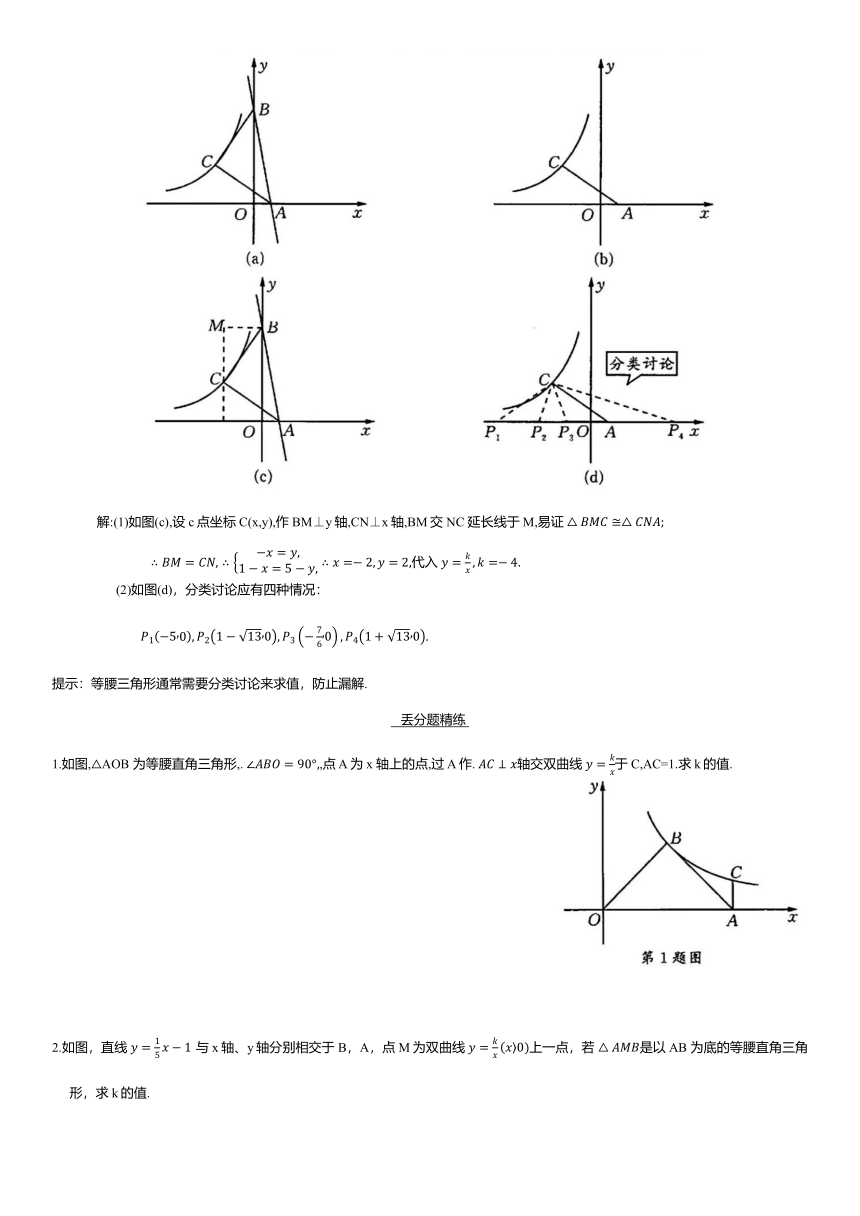
例1 如图(a),直线y=kx-2k交坐标轴于A,B两点,P(m,n)为直线上一点,且满足
(1)求m,n,k的值.
(2)Q 为双曲线 上一点,且∠APQ=45°,求 Q点坐标.
解: 将 P(1,-2)代入y=kx-2k,k=2.
(2)如图(b),∵直线 AB:y=2x-4,∴A(2,0),设直线 PQ交x轴于 D 点,过 D 点作 DC⊥BA 于 C 点,依题意△PCD 为等腰直角三角形.
作 CM⊥x轴于M,PN⊥CN于N,可证:△CNP≌△CMD,∴C(3,2),D(7,0);设 PD:y=kx+b,代入 P(1,-2),D(7,0),
得 联立 化简得 即(x-10)(x+3)=0; (舍),∴Q(10,1).
提示:与45°角有关的问题,通常须要构造直角等腰三角形加以解决.模型的构造往往是初学者的一个难点.
例2 如图(a),已知 A(1,0),C(0,-3),将△AOC 沿AC 翻折得到△ACE,AE 所在的直线交双曲线 于M,N点,试求M,N的坐标.
解:如图(a),过 C 点作 CD∥AE,∵∠OAC=∠EAC,∠EAC=∠DCA,
∴∠OAC=∠DCA,∴AD=CD,设AD=CD=x,
则
∴x=5,故D(-4,0),∴CD:
又 代入A点可得
联立 化简得x -x-6=0,(x-3)(x+2)=0,
提示:角平分线、平行线、等腰三角形三要素在几何构图中常常使用到.利用一次函数图象平行则k值相等可使问题得解.
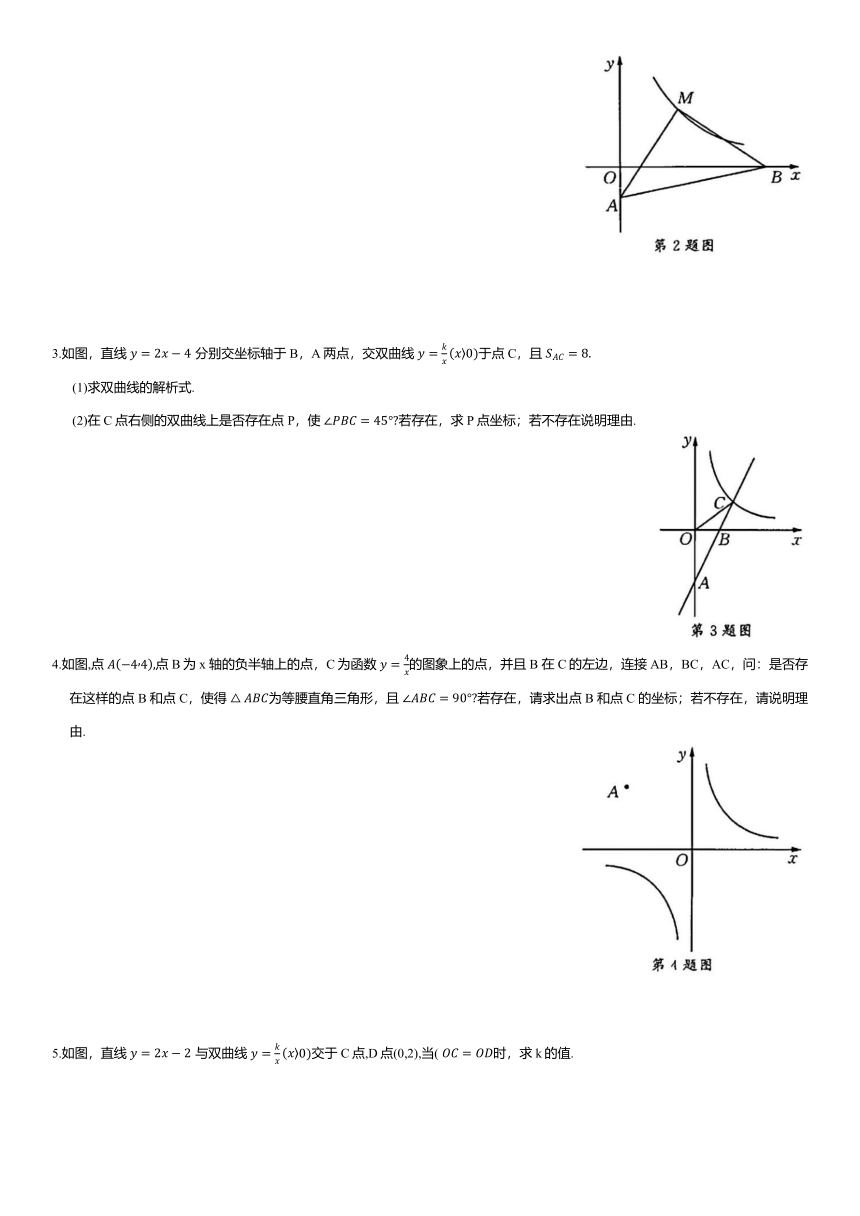
例3 如图(a),y=-5x+5 与坐标轴交于 A,B 两点,△ABC 是以AB 为底边的等腰直角三角形.双曲线 经过C点.
(1)求k的值.
(2)如图(b),P 为x轴上的点,△PAC为等腰三角形,请求出所有可能的 P 点.
解:(1)如图(c),设c点坐标C(x,y),作 BM⊥y轴,CN⊥x轴,BM交 NC 延长线于M,易证
代入
(2)如图(d),分类讨论应有四种情况:
提示:等腰三角形通常需要分类讨论来求值,防止漏解.
丢分题精练
1.如图,△AOB 为等腰直角三角形,. ,点 A 为x 轴上的点,过 A 作. 轴交双曲线 于C,AC=1.求k的值.
2.如图,直线 与x轴、y轴分别相交于 B,A,点 M为双曲线 上一点,若 是以AB 为底的等腰直角三角形,求 k的值.
3.如图,直线 分别交坐标轴于 B,A两点,交双曲线 于点C,且
(1)求双曲线的解析式.
(2)在 C点右侧的双曲线上是否存在点 P,使 若存在,求 P 点坐标;若不存在说明理由.
4.如图,点 点B为x 轴的负半轴上的点,C为函数 的图象上的点,并且 B 在C的左边,连接AB,BC,AC,问:是否存在这样的点 B 和点C,使得 为等腰直角三角形,且 若存在,请求出点 B 和点C 的坐标;若不存在,请说明理由.
5.如图,直线 与双曲线 交于C点,D点(0,2),当( 时,求k的值.
6.如图,直线交坐标轴于A(a,0),B(0,b)两点,且a,b满足 ,AB 平分 OC 交反比例函数 于C点.
(1)求a,b的值.
(2)求 的面积.
7.如图(a),已知直线 交坐标轴于 A,B 两点,C为OA 上一点,且.
(1)求 C点坐标.
(2)如图(b),BE平分. 交BE 于 E点.双曲线 经过E点,求k值.
8.如图(a), 交坐标轴于A,B 两点,交 于C点, 的面积为6.
(1)求 k值.
(2)如图(b),D为反比例函数上的另一点,连CD,过 D 作. 交x轴于E点,且 ED,求E点坐标.
9.如图(a),反比例函数 的图象经过点. ,过点 A 作. 轴于 B, 的面积为
(1)求k和b的值.
(2)若一次函数 的图象经过点A,并且与x轴交于点M,求m的值.
(3)如图(b),在 x轴上是否存在点 P,使 为等腰三角形 若存在,求出所有的 P 点;若不存在,请说明理由.
10.如图(a),正方形OABC的边长为4,双曲线 交 AB于 M,且.
(1)求 k 的值.
(2)如图(b),P 是双曲线上的点,且OP⊥MC,求 P 点坐标.
(3)如图(c),N 是 BC 与双曲线 的交点,NE⊥OA 于 E,问直线 NE 上是否存在点F,使得△MAF 是腰长为3 的等腰三角形 若存在,求出所有可能的点 F;若不存在,说明理由.
11.如图,已知正比例函数. 与反比例函数 的图象交于点 A(3,2).
(1)求上述两函数的表达式.
(2)M(m,n)是反比例函数图象上的一个动点,其中( ,过点 M作直线. 轴交y轴于点 B;过点 A 作直线 轴交x轴于点C,交直线 MB 于点 D,若四边形 OADM的面积为6,求M点坐标.
(3)探索:x轴上是否存在点P,使 是等腰三角形 若存在,求出所有可能的点 P;若不存在,说明理由.
丢分题精析
例1 如图(a),直线y=kx-2k交坐标轴于A,B两点,P(m,n)为直线上一点,且满足
(1)求m,n,k的值.
(2)Q 为双曲线 上一点,且∠APQ=45°,求 Q点坐标.
解: 将 P(1,-2)代入y=kx-2k,k=2.
(2)如图(b),∵直线 AB:y=2x-4,∴A(2,0),设直线 PQ交x轴于 D 点,过 D 点作 DC⊥BA 于 C 点,依题意△PCD 为等腰直角三角形.
作 CM⊥x轴于M,PN⊥CN于N,可证:△CNP≌△CMD,∴C(3,2),D(7,0);设 PD:y=kx+b,代入 P(1,-2),D(7,0),
得 联立 化简得 即(x-10)(x+3)=0; (舍),∴Q(10,1).
提示:与45°角有关的问题,通常须要构造直角等腰三角形加以解决.模型的构造往往是初学者的一个难点.
例2 如图(a),已知 A(1,0),C(0,-3),将△AOC 沿AC 翻折得到△ACE,AE 所在的直线交双曲线 于M,N点,试求M,N的坐标.
解:如图(a),过 C 点作 CD∥AE,∵∠OAC=∠EAC,∠EAC=∠DCA,
∴∠OAC=∠DCA,∴AD=CD,设AD=CD=x,
则
∴x=5,故D(-4,0),∴CD:
又 代入A点可得
联立 化简得x -x-6=0,(x-3)(x+2)=0,
提示:角平分线、平行线、等腰三角形三要素在几何构图中常常使用到.利用一次函数图象平行则k值相等可使问题得解.
例3 如图(a),y=-5x+5 与坐标轴交于 A,B 两点,△ABC 是以AB 为底边的等腰直角三角形.双曲线 经过C点.
(1)求k的值.
(2)如图(b),P 为x轴上的点,△PAC为等腰三角形,请求出所有可能的 P 点.
解:(1)如图(c),设c点坐标C(x,y),作 BM⊥y轴,CN⊥x轴,BM交 NC 延长线于M,易证
代入
(2)如图(d),分类讨论应有四种情况:
提示:等腰三角形通常需要分类讨论来求值,防止漏解.
丢分题精练
1.如图,△AOB 为等腰直角三角形,. ,点 A 为x 轴上的点,过 A 作. 轴交双曲线 于C,AC=1.求k的值.
2.如图,直线 与x轴、y轴分别相交于 B,A,点 M为双曲线 上一点,若 是以AB 为底的等腰直角三角形,求 k的值.
3.如图,直线 分别交坐标轴于 B,A两点,交双曲线 于点C,且
(1)求双曲线的解析式.
(2)在 C点右侧的双曲线上是否存在点 P,使 若存在,求 P 点坐标;若不存在说明理由.
4.如图,点 点B为x 轴的负半轴上的点,C为函数 的图象上的点,并且 B 在C的左边,连接AB,BC,AC,问:是否存在这样的点 B 和点C,使得 为等腰直角三角形,且 若存在,请求出点 B 和点C 的坐标;若不存在,请说明理由.
5.如图,直线 与双曲线 交于C点,D点(0,2),当( 时,求k的值.
6.如图,直线交坐标轴于A(a,0),B(0,b)两点,且a,b满足 ,AB 平分 OC 交反比例函数 于C点.
(1)求a,b的值.
(2)求 的面积.
7.如图(a),已知直线 交坐标轴于 A,B 两点,C为OA 上一点,且.
(1)求 C点坐标.
(2)如图(b),BE平分. 交BE 于 E点.双曲线 经过E点,求k值.
8.如图(a), 交坐标轴于A,B 两点,交 于C点, 的面积为6.
(1)求 k值.
(2)如图(b),D为反比例函数上的另一点,连CD,过 D 作. 交x轴于E点,且 ED,求E点坐标.
9.如图(a),反比例函数 的图象经过点. ,过点 A 作. 轴于 B, 的面积为
(1)求k和b的值.
(2)若一次函数 的图象经过点A,并且与x轴交于点M,求m的值.
(3)如图(b),在 x轴上是否存在点 P,使 为等腰三角形 若存在,求出所有的 P 点;若不存在,请说明理由.
10.如图(a),正方形OABC的边长为4,双曲线 交 AB于 M,且.
(1)求 k 的值.
(2)如图(b),P 是双曲线上的点,且OP⊥MC,求 P 点坐标.
(3)如图(c),N 是 BC 与双曲线 的交点,NE⊥OA 于 E,问直线 NE 上是否存在点F,使得△MAF 是腰长为3 的等腰三角形 若存在,求出所有可能的点 F;若不存在,说明理由.
11.如图,已知正比例函数. 与反比例函数 的图象交于点 A(3,2).
(1)求上述两函数的表达式.
(2)M(m,n)是反比例函数图象上的一个动点,其中( ,过点 M作直线. 轴交y轴于点 B;过点 A 作直线 轴交x轴于点C,交直线 MB 于点 D,若四边形 OADM的面积为6,求M点坐标.
(3)探索:x轴上是否存在点P,使 是等腰三角形 若存在,求出所有可能的点 P;若不存在,说明理由.
