苏科版八年级数学上册6.5《一次函数与二元一次方程组》导学案(无答案)
文档属性
| 名称 | 苏科版八年级数学上册6.5《一次函数与二元一次方程组》导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 44.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-07 00:00:00 | ||
图片预览

文档简介
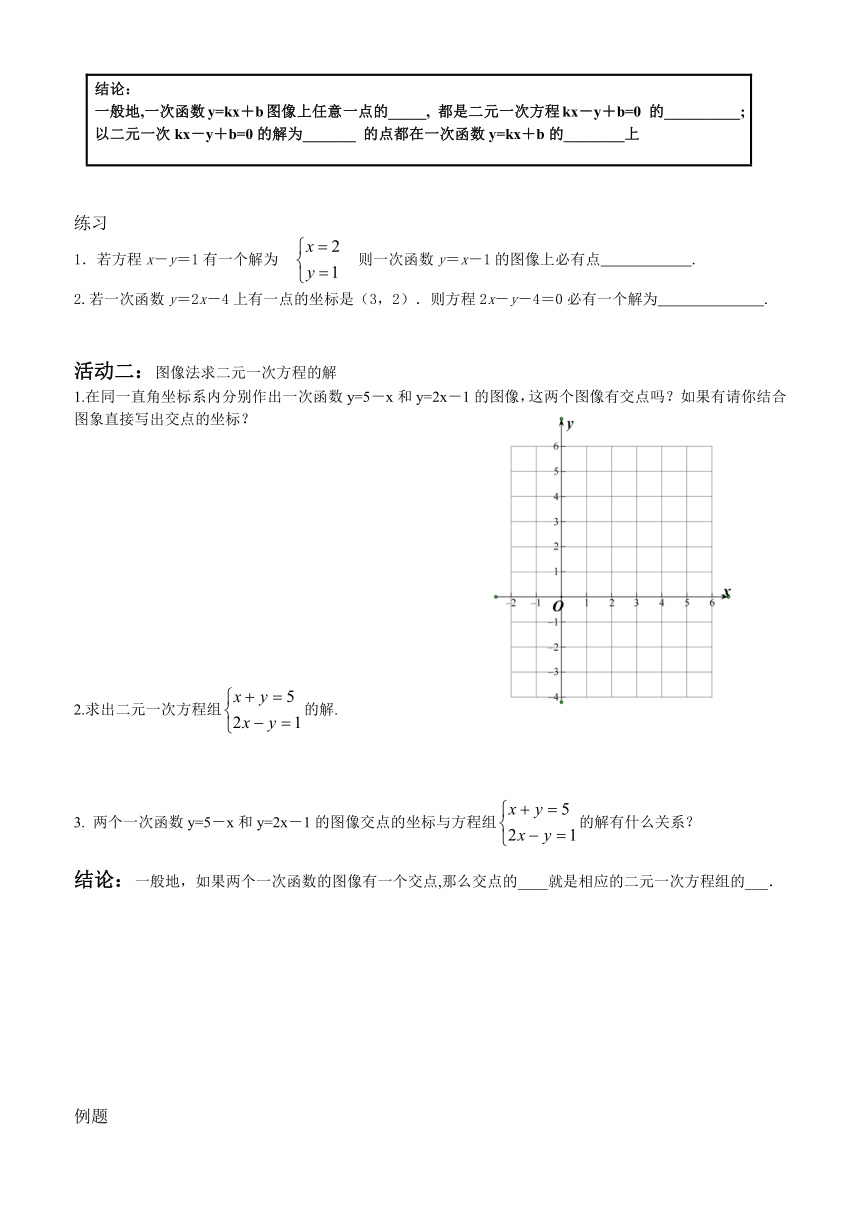
课题:6.5 一次函数与二元一次方程
课型:新授 课时:1 主备:张金萍 审核:八年级数学备课组
姓名_______ 时间:
【学习目标】
1理解一次函数图象上的坐标与二元一次方程的解关系.
2.用图像法求二元一次方程组近视解,体会知识之间的普通联系和知识之间的相互转换.
3.经历探索一次函数与二元一次方程(组)内在联系,进一步感受数形结合思想.
【重点、难点】
1、二元一次方程的解和一次函数图象上点的坐标之间关系.
2、方程和函数之间的对应关系即数形结合理解.
【学习过程】
一、课前准备
1.写出二元一次方程的一个解 .
3.把下列二元一次方程写成一次函数y=kx +b (k0) 的形式。
(1)3x+y=7,
(2)x-2y-3=0
二、探索新知
活动一:二元一次方程与一次函数的关系
(1)方程x+y=5的解有多少个?写出其中的5个解来.(2)在下图中分别描出以这些解为坐标的点.(3)画出的这些点在一次函数的图象上吗? (1)一次函数的图象是什么?(2)在下图中画出一次函数图象.(3)写出图象上任意5点的坐标,它适合方程x+y=5吗?
结论:一般地,一次函数y=kx+b图像 ( http: / / www.21cnjy.com )上任意一点的_____, 都是二元一次方程kx-y+b=0 的__________;以二元一次kx-y+b=0的解为_______ 的点都在一次函数y=kx+b的________上
练习
1.若方程x-y=1有一个解为 则一次函数y=x-1的图像上必有点 .
2.若一次函数y=2x-4上有一点的坐标是(3,2).则方程2x-y-4=0必有一个解为 .
活动二:图像法求二元一次方程的解
1.在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图像,这两个图像有交点吗?如果有请你结合图象直接写出交点的坐标?
2.求出二元一次方程组的解.
3. 两个一次函数y=5-x和y=2x-1的图像交点的坐标与方程组的解有什么关系?
结论:一般地,如果两个一次函数的图像有一个交点,那么交点的____就是相应的二元一次方程组的___.
例题
利用一次函数的图象解二元一次方程组
三、当堂反馈
1.把二元一次方程2x-y-3=0写成一次函数y= ;
2.若一次函数y=-x-2与y=2x-7的图象交点为(2,-3),则二元一次方程组的解为 .
3.因为的解是,所以一次函数y=-x+4与y=2x+1的图象交点坐标为 .
4.直线y=3x-2和y=-2x+3图象的交点坐标为__________.
四、学习目标调查
1、 本课学习目标掌握情况请您在相应的项打√
熟练掌握□ 一般掌握□ 没有明白□
2、本课自己还有疑惑的地方:
五、课后练习
1、直线y=x+3与y=-3x-1的交点坐标为 。
2、已知一次函数y=和y=-的图象交于点A(-2,0),与y轴分别交于B、C两点,那么△ABC的面积为 。
3、利用图解二元一次方程组。
x+y=3
3x-y=5
4、当自变量x取何值时,函数y=与函数y=5x+17的值相等?这个函数值是什么?
5.在图中的两直线l1、l2的交点坐标可以看作__________________的解。
6.已知直线y=3x与y=-x+4,求:⑴这两条直线的交点.⑵这两条直线与y轴围成的三角形面积.
7.已知直线经过原点和点(-2,-4),直线经过点(1,5)和点(8,-2),求:
y和y的函数关系式,并在同一坐标系中画出函数图象;
若两直线交于点M,求M的坐标;
若直线y与x轴交于点N,试求三角形MON的面积。
8.在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示。请根据图象所提供的信息回答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是 ;
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等?
课型:新授 课时:1 主备:张金萍 审核:八年级数学备课组
姓名_______ 时间:
【学习目标】
1理解一次函数图象上的坐标与二元一次方程的解关系.
2.用图像法求二元一次方程组近视解,体会知识之间的普通联系和知识之间的相互转换.
3.经历探索一次函数与二元一次方程(组)内在联系,进一步感受数形结合思想.
【重点、难点】
1、二元一次方程的解和一次函数图象上点的坐标之间关系.
2、方程和函数之间的对应关系即数形结合理解.
【学习过程】
一、课前准备
1.写出二元一次方程的一个解 .
3.把下列二元一次方程写成一次函数y=kx +b (k0) 的形式。
(1)3x+y=7,
(2)x-2y-3=0
二、探索新知
活动一:二元一次方程与一次函数的关系
(1)方程x+y=5的解有多少个?写出其中的5个解来.(2)在下图中分别描出以这些解为坐标的点.(3)画出的这些点在一次函数的图象上吗? (1)一次函数的图象是什么?(2)在下图中画出一次函数图象.(3)写出图象上任意5点的坐标,它适合方程x+y=5吗?
结论:一般地,一次函数y=kx+b图像 ( http: / / www.21cnjy.com )上任意一点的_____, 都是二元一次方程kx-y+b=0 的__________;以二元一次kx-y+b=0的解为_______ 的点都在一次函数y=kx+b的________上
练习
1.若方程x-y=1有一个解为 则一次函数y=x-1的图像上必有点 .
2.若一次函数y=2x-4上有一点的坐标是(3,2).则方程2x-y-4=0必有一个解为 .
活动二:图像法求二元一次方程的解
1.在同一直角坐标系内分别作出一次函数y=5-x和y=2x-1的图像,这两个图像有交点吗?如果有请你结合图象直接写出交点的坐标?
2.求出二元一次方程组的解.
3. 两个一次函数y=5-x和y=2x-1的图像交点的坐标与方程组的解有什么关系?
结论:一般地,如果两个一次函数的图像有一个交点,那么交点的____就是相应的二元一次方程组的___.
例题
利用一次函数的图象解二元一次方程组
三、当堂反馈
1.把二元一次方程2x-y-3=0写成一次函数y= ;
2.若一次函数y=-x-2与y=2x-7的图象交点为(2,-3),则二元一次方程组的解为 .
3.因为的解是,所以一次函数y=-x+4与y=2x+1的图象交点坐标为 .
4.直线y=3x-2和y=-2x+3图象的交点坐标为__________.
四、学习目标调查
1、 本课学习目标掌握情况请您在相应的项打√
熟练掌握□ 一般掌握□ 没有明白□
2、本课自己还有疑惑的地方:
五、课后练习
1、直线y=x+3与y=-3x-1的交点坐标为 。
2、已知一次函数y=和y=-的图象交于点A(-2,0),与y轴分别交于B、C两点,那么△ABC的面积为 。
3、利用图解二元一次方程组。
x+y=3
3x-y=5
4、当自变量x取何值时,函数y=与函数y=5x+17的值相等?这个函数值是什么?
5.在图中的两直线l1、l2的交点坐标可以看作__________________的解。
6.已知直线y=3x与y=-x+4,求:⑴这两条直线的交点.⑵这两条直线与y轴围成的三角形面积.
7.已知直线经过原点和点(-2,-4),直线经过点(1,5)和点(8,-2),求:
y和y的函数关系式,并在同一坐标系中画出函数图象;
若两直线交于点M,求M的坐标;
若直线y与x轴交于点N,试求三角形MON的面积。
8.在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示。请根据图象所提供的信息回答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是 ;
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
