人教版七年级数学上册课件3.3解一元一次方程(二)—去括号与去分母(共72张PPT)
文档属性
| 名称 | 人教版七年级数学上册课件3.3解一元一次方程(二)—去括号与去分母(共72张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-09 00:00:00 | ||
图片预览











文档简介
课件72张PPT。 巴甫洛维奇·契诃夫是19世纪末俄国现实主义代表作家之一,是杰出的短篇小说家与戏剧家.他在上大学期间,就为当时的幽默杂志撰写短篇小说.契诃夫的作品对俄国文学和戏剧的发展有重大影响.他对数学也很感兴趣,在短篇小说《家庭教师》中就有下面一道趣题: 新课导入 某商人花540卢布买了黑布料和蓝布料共138俄尺,已知蓝布料每俄尺5卢布,黑布料每俄尺3卢布.请问商人买来黑布料、蓝布料各有几俄尺? 如何解决这个问题呢?(卢布和俄尺分别是俄罗斯的货币单位和长度单位) 解:设买了蓝布料x俄尺,那么买黑布料(138-x)俄尺;因而买蓝布料花了3x卢布,买黑布料花了5(138-x)卢布,根据买两种布料共用540卢布,列得方程
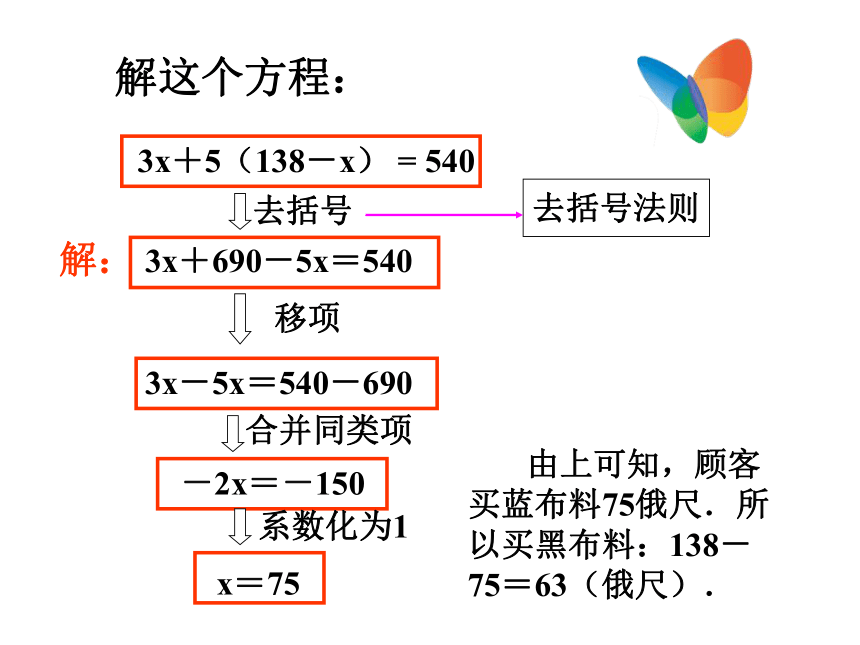
3x+5(138-x) = 540怎样使这个方程转化为x = a的形式?3.3 解一元一次方程(二)
——去括号与去分母知识与能力
1.掌握解一元一次方程中“去分母”、“去括号”的方法,并能解此类型的方程.
2.了解一元一次方程解法的一般步骤.教学目标过程与方法
1.通过运用算术和列方程两种方法解决实际问题的过程,体会到列方程解应用题更为简捷明了;掌握去括号解方程的方法,会用去分母的方法解一元一次方程.
2.培养分析问题,解决问题的能力.教学目标情感态度与价值观
通过列方程解决实际问题,感受数学的应用价值,激发学习数学的信心.教学目标重点
解含有括号、分母的一元一次方程的解法.
难点
1.弄清列方程解应用题的思想方法;
2.会用去括号、去分母解一元一次方程. 教学重难点化简下列各式:(1)3a+2b+(6a-4b)(2)(-3a+2b) +3(a-b)(3)-5a+4b-(-3a+b)9a-2b-b-2a+3b想一想去括号时符号变化规律.去括号法则
1.括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
2.括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.知识回顾解这个方程:解:去括号移项合并同类项系数化为1去括号法则 由上可知,顾客买蓝布料75俄尺.所以买黑布料:138-75=63(俄尺). 问题:王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了44 000元,其中种茄子每亩用了1700元,种西红柿每亩用了1800元.问两蔬菜各种了多少亩? 分析:设王大伯共种了x亩茄子,则他种西红柿__________亩.种茄子每亩用了1700元.那么种茄子一共用去了________元; 种西红柿每亩用了1800元,则他种西红柿共用去了______________元.根据王大伯种这两种蔬菜共用去了44000元,可列方程
(25-x)1700x1800 (25-x)1700x+ 1800 (25-x)=44 000.怎样解这个方程?去括号移项合并同类项系数化为1去括号是解方程时常用的变形.解:由上可知,种茄子10亩.
所以种西红柿:25-10=15(亩).
答:种茄子10亩,种西红柿15亩. 例1 解方程
(1)x+5(2x-1)=3-2(-x-5)解:去括号,得
x+10x-5=3+2x+10
移项,得
x+10x-2x=3+10+5
合并同类项,得
9x=18
系数化为1,得
x=2.(2)4x-3(15-x) =6x-7(11-x)解:去括号,得
4x-45+3x=6x-77+7x
移项,得
4x+3x-6x-7x=-77+45
合并同类项,得
-6x=-32
系数化成1,得 讨论:解一元一次方程的步骤是什么?(1)去括号
(2)移项
(3)合并同类项
(4)系数化成1(1) 3x-5(x-3)=9-(x+4)(2) 6x =-2(3x-5) +10
(3) -2(x+5)=3(x-5) -6 解下列方程.x=10x=14练一练 1.某校准备将2000元奖金全部发给20名三好生,其中市级三好生每人得奖金200元,校级三好生每人得奖金50元,请问全校市级三好生、校级三好生各有多少人?解:高全校市级三好生x人,列方程
200x+50(20-x) =2000
解,得x=5.
所以校级三好生: 20-x=15(人)
答:市级三好生5人;校级三好生15人.练一练 2.一个笼中装有鸡、兔若干只,从上面看,共有21个头;从下面看,共有66只脚,问鸡、兔各有多少只.解:设鸡x只,列方程
2x+4(21-x) =66
解,得 x=9
所以兔的个数为:21-x=12(只)
答:笼中有鸡9只,兔12只. (3)李白街上走,提壶去买酒,遇店加一倍,见花喝一斗;三遇店和花,喝光壶中酒,试问酒壶中原有多少酒?斗:古代的一个计量单位;
1斗 = 10升 .解:设:设酒壶中原有x斗酒.
第一次遇店:
第一次遇花:
第二次遇店:
第二次遇花:
第三次遇店:
第三次遇花:2x2x-1=2x-12(2x-1) =4x-24x-2 -1=4x-32(4x-3) =8x-68x-6-1=8x-7列方程,得8x-7=0
解,得
x=0.875答:酒壶中原有0.875斗酒. 例2:一艘轮船在两个码头之间航行,顺水航行需要4小时,逆水行驶需要5小时,水流的速度是2千米/时,求轮船在静水中的行驶速度.分析:已知两个码头之间的距离相等
所以:顺流速度×顺流时间=逆流速度×逆流时间 去括号,得
4x+8=5x-10
移项及合并同类项,得
-x=-18
系数化为1,得
x=18.
答:船在静水中的行驶速度为18千米/时.解:设轮船在静水中的行驶速度为x千米/时,
则顺流速度为(x +2)千米/时,逆流速
度为(x-2 )千米/时.
可列方程
4× (x +2)=5× (x-2 ) 常用的关系式
顺流时的速度=静水中的速度+水流的速度
逆流时的速度=静水中的速度-水流的速度归纳 (1) 一艘轮船从一码头逆流而上,再顺流而下.如果轮船在静水中的速度为每小时15千米,水流速度为每小时3千米,那么这艘轮船最多开出多远然后返回才能保证在 7.5小时内回到原码头? 解:设这艘轮船开出x小时后多返回,才能保证在 7.5小时内回到原码头. 列方程
(15-3)x=(15+3) ×(7.5-x)
解,得: x=4.5
即轮船开出后: (15-3)x=54(千米)后,返回才能保证在 7.5小时内回到原码头. 练一练 (2) 甲、乙两人在一条长400米的环形跑道上跑步.甲的速度是360米/分,乙的速度是240米/分.
1. 两人同时同地同向跑,多长时间两人第一次相遇,此时两人一共跑了几圈?
2. 两人同时同地反向跑,几秒后两人第一次相遇?
3. 两人同时同向跑,甲先跑30秒,问还要多长时间两人第一次相遇?
4. 两人同时同向跑,乙先跑30秒,问还要多长时间两人第一次相遇? 54011秒26秒 (3)一小船由A港到B港顺流行驶航行需6h,由B港到A港逆流航行需要8h,一天,小船从早晨6时由A港出发顺流到达B港时,发现救生圈在途中掉落了水中,立即返回,1h后找到救生圈. 1. 若小船按水流速度由A港漂流到B港,需要多长时间?
2. 救生圈是在什么时候掉入水中的? 48小时11时 例3:(1)某工厂计划用26小时生产一批零件,后因每小时多生产5件,用24小时不但完成了任务,而且比原计划多生产了60件,问原计划生产多少件零件? 分析:原计划生产x件零件,所以
计划每小时生产零件数×26=实际每小时生产零件数×24-60.解:设原计划每小时生产x件零件,列方程
??? 24x×(x+5) -60=26x
去括号,得
????? ? 24x+120-60=26x
移项及合并同类项,得
?????????2x=60
系数化成1,得
?????????x=30
??????????所以原计划26×30=780(件)
答:原计划生产780件零件. (2)一个服装车间,共有90人,每人每小时加工1件衣服或2条裤子,问怎样安排工作才能使衣服和裤子正好配套?(一件衣服配一条裤子) 分析:为了使每天生产的衣服和裤子正好配套,应使生产的衣服和裤子数量相等. 解:设做衣服人数为x人,则做裤子的人数为(90-x)人.列方程
x=2(90-x)
去括号,得
x=180-2x??
移项及合并同类项,得
3x=180
系数化为1,得
x=60.
所以做裤子的人数为: 60-x=20(人).
答:做衣服人的人数为40人,做裤子的人为20人. (1)某车间每天能生产甲种零件100个,或者乙种零件100个.甲、乙两种零件分别取3个、2个才能配成一套.要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数? 解:设生产甲种零件x天,列方程:
2×100x=3×100(30-x)
解,得:
x=18
则生产乙种零件的天数为:30-x=12(天)
答:应安排生产甲种零件18天,乙种零件12天.练一练 (2)某水利工地派40人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走? 解:设每天派x人挖土,列方程
5x=3(40-x)
解,得
x=15
所以每天运土人数为: 40-x=25(人)
答:每天派15人挖土,25人运土,正好能使挖出的土及时运走. (3)用白铁皮做罐头盒,每张铁片可制盒身16个或制盒底45个一个盒身与两个盒底配成一套罐头盒.现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分地利用白铁皮? 解:设x张白铁皮做盒身,列方程
2×16x=45×(100-x)
解,得
x=60
则做盒底的铁皮为:100-x=40(张)
答:用60张白铁皮做盒身,40张白铁皮做盒底. 目前初中数学主要分成代数与几何两大部分,其中代数学的最大特点是引人了未知数,建立方程,对未知数加以运算.而最早提出这一思想并加以举例论述的,是古代数学名著《算术》一书,其作者是古希腊后期数学家一“代数学之父”丢番图. 丢番图是希腊数学家,他的13卷巨著《算术》在代数符号、数论、代数方程解法等方面均有重要贡献,其不定方程理论对后世产生了巨大影响,以至后人把整系数不定方程称为“丢番图方程”.
关于丢番图的生平,我们仅能从其墓志铭中略知梗概,这篇墓志铭本身就是一个有趣的数学问题,因为被4世纪数学家麦特劳德尔收入一部数学问题集中,得以流传至今:丢番图的生平读一读 这是一座石墓,
里面安葬着丢番图.
请你告诉我,
丢番图寿数几何?
他一生的六分之一是幸福的童年,
十二分之一是无忧无虑的少年.
再过去七分之一的年程,
他建立了幸福的家庭.
五年之后儿子出生,
不料儿子竟先其父四年而终,
只活到父亲一半的年龄.
晚年丧子老人真可怜,
悲痛之中渡过风烛残年.
请你告诉我,
丢番图寿数几何? 解:设丢番图去世时的年龄为x岁,由题意可列方程 怎样使这个方程转化为x = a的形式? 请你列出方程算一算,丢番图去世时的年龄? 分析:
为使方程变为整系数方程,方程两边应该同乘以什么数?各分母的最小公倍数84.去分母(方程两边同乘各分母的最小分倍数) 移项 系数化为1 答:丢番图去世时的年龄为84岁.合并同类项 解: 这件珍贵的文物是纸莎草文书,是古代埃及人用象形文字写在一种特殊的草上的著作,至今已有3700多年的历史了,在文书中记载了许多有关数学的问题. 问题: 一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33. 解:设这个数为x,可得方程: 为使方程变为整系数方程,方程两边应该同乘以什么数?各分母的最小公倍数42.解:去分母,得
28x+21x+6x+42x=1386.
合并同类项,得
97x=1386.
系数化为1,得归纳去分母时须注意
1.确定各分母的最小公倍数;
2.不要漏乘没有分母的项;
3.去掉分母后,若分子是多项式,要加括号,视多项式为一整体. 解有分数系数的一元一次方程的步骤:
1.去分母;
2.去括号;
3.移项;
4.合并同类项;
5.系数化为1.主要依据:等式的性质和运算律等.归纳以上步骤是不是一定要顺序进行,缺一不可? (1)碧空万里,一群大雁在飞翔,迎面又飞来一只小灰雁,它对群雁说:“你们好,百只雁!你们百雁齐飞,好气派!可怜我是孤雁独飞.”群雁中一只领头的老雁说:“不对!小朋友,我们远远不足100只.将我们这一群加倍,再加上半群,又加上四分之一群,最后还得请你也凑上,那才一共是100只呢,请问这群大雁有多少只? 解:设这群大雁有x只,
列方程解方程,得
x=36提示:练一练 (2)火车用26秒的时间通过一个长256米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16秒的时间通过了长96米的隧道,求火车的长度. 解:设火车长度为x米,列方程 解,得 x=160
答:火车的长度为160米.例4:解方程 解:去分母(方程两边同乘12),得
3(x-1) -4(2x+5) =-3×12
去括号,得
3x-3-8x-20=-36
移项,得
3x-8x=-36+3+20
合并同类项,得
-5x=-13
系数化为1,得解:去分母(方程两边同乘12),得
4(-x+4)-12x+5×12=4(x-3)-3(x-1)
去括号,得
-4x-16-12x+60=4x-12-3x+3
移项,得
-4x-12x-4x+3x=-12+3+16-60
合并同类项,得
-17x=-53
系数化为1,得解:去分母(两边同乘12),得
8(x-6) =3(-2x-3) -2
去括号,得
8x-48=-6x-9-2
移项,得
8x+6x=-9-2+48
合并同类项,得
14x=37
系数化为1,得解下列方程:练一练 例5:(1)一件工作,甲单独做25小时完成,乙单独做12小时完成.那么两人合作多少小时完成?分析:本题是一个典型的工程类应用题.
甲单独做20小时完成的工作量+乙单独做12小时完成的工作量=完成的工作总量1 解:设两人合作x小时完成此工作,
可列方程 答:两人合作6小时完成.?去分母,得
4x+6x=60
合并同类项,得
x=6 (2)一件工作,甲单独做15小时完成,乙单独做12小时完成.甲先单独做6小时,然后乙加入合作,那么两人合作还要多少小时完成? 分析:把总工作量看作是1.
设还要x小时才能完成工作.
甲的工作总量+乙的工作总量=总工作量1.答:两人合作还要4小时完成. 解:设两人合作还需x小时完成此工作,列方程去分母,得
4x+24+5x=60
移项及合并同类项,得
9x=36
系数化为1,得
x=4 (3)一件工作,甲单独做15小时完成,甲、乙合做6小时完成.甲先单独做6小时,余下的乙单独做,那么乙还要多少小时完成? 分析:把总工作量看作是1.
设乙还要x小时才能完成工作.
甲的工作总量+乙的工作总量=总工作量1.答:乙还要6小时完成.解:设乙还需x小时完成此工作,依题意可得:去分母,得
24+(10-4)x=60
去括号,得
24+6x=60
移项,得
6x=36
系数化为1,得
x=6工程问题
1.工作量、工作时间、工作效率;
2.这三个基本量的关系是:
工作量=工作时间×工作效率
工作效率=工作量÷工作时间
工作时间=工作量÷工作效率
3.工作总量通常看作单位“1”归纳 小明预定搭乘家门口的公共汽车赶往火车站,去家乡看望爷爷.在行驶了三分之一路程后,估计继续乘公共汽车将会在火车开车后半小时到达火车站,便随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前15分钟到达火车站.已知公共汽车的平均速度是40千米/时,问小明家到火车站有多远?练一练 解:设小明家到火车站路程的 为x千米,列方程:解,得
x=60
则小明家到火车站的路程为90千米.答:小明家到火车站的路程为90千米.1.解一元一次方程的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项,化为最简方程ax=b(a≠0)的形式;
(5)系数化为1.2. 用一元一次方程解决实际问题方面.课堂小结 1.某工厂今年3月份的产量是50万元,5月份上升到72万元,设这两个月的平均增长率为x,则( )
A.50(1+x) =72
B.50(1+x) +50(1+x)2=72
C.50(1+x)x2=72
D.50(1+x)2=72D随堂练习 2.甲、乙二人按2:5的比例投资开办了一家公司,约定除去各项开支外,所得利润投资比例分成,若第一年赢得1400元,那么甲、乙二人分别应分得( )
A.2000元和5000元
B.5000元和2000元
C.4000元和10000元
D.10000元和4000元C3.解下列方程:x=2x=-324.讨论关于x的方程ax=b,的情况. 5.已知2x+1与-12x+5的值是相反数,求x的值.解:根据题意得:
(2x+1)+(-12x+5)=0
去括号,得
2x+1-12x+5=0
称项,得
2x-12x=-1-5
合并同类项,得
-10x=-6
系数化为1,得
x=0.6
答:x的值为0.6.解:根据题意,得解,得6.习题答案
3x+5(138-x) = 540怎样使这个方程转化为x = a的形式?3.3 解一元一次方程(二)
——去括号与去分母知识与能力
1.掌握解一元一次方程中“去分母”、“去括号”的方法,并能解此类型的方程.
2.了解一元一次方程解法的一般步骤.教学目标过程与方法
1.通过运用算术和列方程两种方法解决实际问题的过程,体会到列方程解应用题更为简捷明了;掌握去括号解方程的方法,会用去分母的方法解一元一次方程.
2.培养分析问题,解决问题的能力.教学目标情感态度与价值观
通过列方程解决实际问题,感受数学的应用价值,激发学习数学的信心.教学目标重点
解含有括号、分母的一元一次方程的解法.
难点
1.弄清列方程解应用题的思想方法;
2.会用去括号、去分母解一元一次方程. 教学重难点化简下列各式:(1)3a+2b+(6a-4b)(2)(-3a+2b) +3(a-b)(3)-5a+4b-(-3a+b)9a-2b-b-2a+3b想一想去括号时符号变化规律.去括号法则
1.括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
2.括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.知识回顾解这个方程:解:去括号移项合并同类项系数化为1去括号法则 由上可知,顾客买蓝布料75俄尺.所以买黑布料:138-75=63(俄尺). 问题:王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,用去了44 000元,其中种茄子每亩用了1700元,种西红柿每亩用了1800元.问两蔬菜各种了多少亩? 分析:设王大伯共种了x亩茄子,则他种西红柿__________亩.种茄子每亩用了1700元.那么种茄子一共用去了________元; 种西红柿每亩用了1800元,则他种西红柿共用去了______________元.根据王大伯种这两种蔬菜共用去了44000元,可列方程
(25-x)1700x1800 (25-x)1700x+ 1800 (25-x)=44 000.怎样解这个方程?去括号移项合并同类项系数化为1去括号是解方程时常用的变形.解:由上可知,种茄子10亩.
所以种西红柿:25-10=15(亩).
答:种茄子10亩,种西红柿15亩. 例1 解方程
(1)x+5(2x-1)=3-2(-x-5)解:去括号,得
x+10x-5=3+2x+10
移项,得
x+10x-2x=3+10+5
合并同类项,得
9x=18
系数化为1,得
x=2.(2)4x-3(15-x) =6x-7(11-x)解:去括号,得
4x-45+3x=6x-77+7x
移项,得
4x+3x-6x-7x=-77+45
合并同类项,得
-6x=-32
系数化成1,得 讨论:解一元一次方程的步骤是什么?(1)去括号
(2)移项
(3)合并同类项
(4)系数化成1(1) 3x-5(x-3)=9-(x+4)(2) 6x =-2(3x-5) +10
(3) -2(x+5)=3(x-5) -6 解下列方程.x=10x=14练一练 1.某校准备将2000元奖金全部发给20名三好生,其中市级三好生每人得奖金200元,校级三好生每人得奖金50元,请问全校市级三好生、校级三好生各有多少人?解:高全校市级三好生x人,列方程
200x+50(20-x) =2000
解,得x=5.
所以校级三好生: 20-x=15(人)
答:市级三好生5人;校级三好生15人.练一练 2.一个笼中装有鸡、兔若干只,从上面看,共有21个头;从下面看,共有66只脚,问鸡、兔各有多少只.解:设鸡x只,列方程
2x+4(21-x) =66
解,得 x=9
所以兔的个数为:21-x=12(只)
答:笼中有鸡9只,兔12只. (3)李白街上走,提壶去买酒,遇店加一倍,见花喝一斗;三遇店和花,喝光壶中酒,试问酒壶中原有多少酒?斗:古代的一个计量单位;
1斗 = 10升 .解:设:设酒壶中原有x斗酒.
第一次遇店:
第一次遇花:
第二次遇店:
第二次遇花:
第三次遇店:
第三次遇花:2x2x-1=2x-12(2x-1) =4x-24x-2 -1=4x-32(4x-3) =8x-68x-6-1=8x-7列方程,得8x-7=0
解,得
x=0.875答:酒壶中原有0.875斗酒. 例2:一艘轮船在两个码头之间航行,顺水航行需要4小时,逆水行驶需要5小时,水流的速度是2千米/时,求轮船在静水中的行驶速度.分析:已知两个码头之间的距离相等
所以:顺流速度×顺流时间=逆流速度×逆流时间 去括号,得
4x+8=5x-10
移项及合并同类项,得
-x=-18
系数化为1,得
x=18.
答:船在静水中的行驶速度为18千米/时.解:设轮船在静水中的行驶速度为x千米/时,
则顺流速度为(x +2)千米/时,逆流速
度为(x-2 )千米/时.
可列方程
4× (x +2)=5× (x-2 ) 常用的关系式
顺流时的速度=静水中的速度+水流的速度
逆流时的速度=静水中的速度-水流的速度归纳 (1) 一艘轮船从一码头逆流而上,再顺流而下.如果轮船在静水中的速度为每小时15千米,水流速度为每小时3千米,那么这艘轮船最多开出多远然后返回才能保证在 7.5小时内回到原码头? 解:设这艘轮船开出x小时后多返回,才能保证在 7.5小时内回到原码头. 列方程
(15-3)x=(15+3) ×(7.5-x)
解,得: x=4.5
即轮船开出后: (15-3)x=54(千米)后,返回才能保证在 7.5小时内回到原码头. 练一练 (2) 甲、乙两人在一条长400米的环形跑道上跑步.甲的速度是360米/分,乙的速度是240米/分.
1. 两人同时同地同向跑,多长时间两人第一次相遇,此时两人一共跑了几圈?
2. 两人同时同地反向跑,几秒后两人第一次相遇?
3. 两人同时同向跑,甲先跑30秒,问还要多长时间两人第一次相遇?
4. 两人同时同向跑,乙先跑30秒,问还要多长时间两人第一次相遇? 54011秒26秒 (3)一小船由A港到B港顺流行驶航行需6h,由B港到A港逆流航行需要8h,一天,小船从早晨6时由A港出发顺流到达B港时,发现救生圈在途中掉落了水中,立即返回,1h后找到救生圈. 1. 若小船按水流速度由A港漂流到B港,需要多长时间?
2. 救生圈是在什么时候掉入水中的? 48小时11时 例3:(1)某工厂计划用26小时生产一批零件,后因每小时多生产5件,用24小时不但完成了任务,而且比原计划多生产了60件,问原计划生产多少件零件? 分析:原计划生产x件零件,所以
计划每小时生产零件数×26=实际每小时生产零件数×24-60.解:设原计划每小时生产x件零件,列方程
??? 24x×(x+5) -60=26x
去括号,得
????? ? 24x+120-60=26x
移项及合并同类项,得
?????????2x=60
系数化成1,得
?????????x=30
??????????所以原计划26×30=780(件)
答:原计划生产780件零件. (2)一个服装车间,共有90人,每人每小时加工1件衣服或2条裤子,问怎样安排工作才能使衣服和裤子正好配套?(一件衣服配一条裤子) 分析:为了使每天生产的衣服和裤子正好配套,应使生产的衣服和裤子数量相等. 解:设做衣服人数为x人,则做裤子的人数为(90-x)人.列方程
x=2(90-x)
去括号,得
x=180-2x??
移项及合并同类项,得
3x=180
系数化为1,得
x=60.
所以做裤子的人数为: 60-x=20(人).
答:做衣服人的人数为40人,做裤子的人为20人. (1)某车间每天能生产甲种零件100个,或者乙种零件100个.甲、乙两种零件分别取3个、2个才能配成一套.要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天数? 解:设生产甲种零件x天,列方程:
2×100x=3×100(30-x)
解,得:
x=18
则生产乙种零件的天数为:30-x=12(天)
答:应安排生产甲种零件18天,乙种零件12天.练一练 (2)某水利工地派40人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走? 解:设每天派x人挖土,列方程
5x=3(40-x)
解,得
x=15
所以每天运土人数为: 40-x=25(人)
答:每天派15人挖土,25人运土,正好能使挖出的土及时运走. (3)用白铁皮做罐头盒,每张铁片可制盒身16个或制盒底45个一个盒身与两个盒底配成一套罐头盒.现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分地利用白铁皮? 解:设x张白铁皮做盒身,列方程
2×16x=45×(100-x)
解,得
x=60
则做盒底的铁皮为:100-x=40(张)
答:用60张白铁皮做盒身,40张白铁皮做盒底. 目前初中数学主要分成代数与几何两大部分,其中代数学的最大特点是引人了未知数,建立方程,对未知数加以运算.而最早提出这一思想并加以举例论述的,是古代数学名著《算术》一书,其作者是古希腊后期数学家一“代数学之父”丢番图. 丢番图是希腊数学家,他的13卷巨著《算术》在代数符号、数论、代数方程解法等方面均有重要贡献,其不定方程理论对后世产生了巨大影响,以至后人把整系数不定方程称为“丢番图方程”.
关于丢番图的生平,我们仅能从其墓志铭中略知梗概,这篇墓志铭本身就是一个有趣的数学问题,因为被4世纪数学家麦特劳德尔收入一部数学问题集中,得以流传至今:丢番图的生平读一读 这是一座石墓,
里面安葬着丢番图.
请你告诉我,
丢番图寿数几何?
他一生的六分之一是幸福的童年,
十二分之一是无忧无虑的少年.
再过去七分之一的年程,
他建立了幸福的家庭.
五年之后儿子出生,
不料儿子竟先其父四年而终,
只活到父亲一半的年龄.
晚年丧子老人真可怜,
悲痛之中渡过风烛残年.
请你告诉我,
丢番图寿数几何? 解:设丢番图去世时的年龄为x岁,由题意可列方程 怎样使这个方程转化为x = a的形式? 请你列出方程算一算,丢番图去世时的年龄? 分析:
为使方程变为整系数方程,方程两边应该同乘以什么数?各分母的最小公倍数84.去分母(方程两边同乘各分母的最小分倍数) 移项 系数化为1 答:丢番图去世时的年龄为84岁.合并同类项 解: 这件珍贵的文物是纸莎草文书,是古代埃及人用象形文字写在一种特殊的草上的著作,至今已有3700多年的历史了,在文书中记载了许多有关数学的问题. 问题: 一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33. 解:设这个数为x,可得方程: 为使方程变为整系数方程,方程两边应该同乘以什么数?各分母的最小公倍数42.解:去分母,得
28x+21x+6x+42x=1386.
合并同类项,得
97x=1386.
系数化为1,得归纳去分母时须注意
1.确定各分母的最小公倍数;
2.不要漏乘没有分母的项;
3.去掉分母后,若分子是多项式,要加括号,视多项式为一整体. 解有分数系数的一元一次方程的步骤:
1.去分母;
2.去括号;
3.移项;
4.合并同类项;
5.系数化为1.主要依据:等式的性质和运算律等.归纳以上步骤是不是一定要顺序进行,缺一不可? (1)碧空万里,一群大雁在飞翔,迎面又飞来一只小灰雁,它对群雁说:“你们好,百只雁!你们百雁齐飞,好气派!可怜我是孤雁独飞.”群雁中一只领头的老雁说:“不对!小朋友,我们远远不足100只.将我们这一群加倍,再加上半群,又加上四分之一群,最后还得请你也凑上,那才一共是100只呢,请问这群大雁有多少只? 解:设这群大雁有x只,
列方程解方程,得
x=36提示:练一练 (2)火车用26秒的时间通过一个长256米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16秒的时间通过了长96米的隧道,求火车的长度. 解:设火车长度为x米,列方程 解,得 x=160
答:火车的长度为160米.例4:解方程 解:去分母(方程两边同乘12),得
3(x-1) -4(2x+5) =-3×12
去括号,得
3x-3-8x-20=-36
移项,得
3x-8x=-36+3+20
合并同类项,得
-5x=-13
系数化为1,得解:去分母(方程两边同乘12),得
4(-x+4)-12x+5×12=4(x-3)-3(x-1)
去括号,得
-4x-16-12x+60=4x-12-3x+3
移项,得
-4x-12x-4x+3x=-12+3+16-60
合并同类项,得
-17x=-53
系数化为1,得解:去分母(两边同乘12),得
8(x-6) =3(-2x-3) -2
去括号,得
8x-48=-6x-9-2
移项,得
8x+6x=-9-2+48
合并同类项,得
14x=37
系数化为1,得解下列方程:练一练 例5:(1)一件工作,甲单独做25小时完成,乙单独做12小时完成.那么两人合作多少小时完成?分析:本题是一个典型的工程类应用题.
甲单独做20小时完成的工作量+乙单独做12小时完成的工作量=完成的工作总量1 解:设两人合作x小时完成此工作,
可列方程 答:两人合作6小时完成.?去分母,得
4x+6x=60
合并同类项,得
x=6 (2)一件工作,甲单独做15小时完成,乙单独做12小时完成.甲先单独做6小时,然后乙加入合作,那么两人合作还要多少小时完成? 分析:把总工作量看作是1.
设还要x小时才能完成工作.
甲的工作总量+乙的工作总量=总工作量1.答:两人合作还要4小时完成. 解:设两人合作还需x小时完成此工作,列方程去分母,得
4x+24+5x=60
移项及合并同类项,得
9x=36
系数化为1,得
x=4 (3)一件工作,甲单独做15小时完成,甲、乙合做6小时完成.甲先单独做6小时,余下的乙单独做,那么乙还要多少小时完成? 分析:把总工作量看作是1.
设乙还要x小时才能完成工作.
甲的工作总量+乙的工作总量=总工作量1.答:乙还要6小时完成.解:设乙还需x小时完成此工作,依题意可得:去分母,得
24+(10-4)x=60
去括号,得
24+6x=60
移项,得
6x=36
系数化为1,得
x=6工程问题
1.工作量、工作时间、工作效率;
2.这三个基本量的关系是:
工作量=工作时间×工作效率
工作效率=工作量÷工作时间
工作时间=工作量÷工作效率
3.工作总量通常看作单位“1”归纳 小明预定搭乘家门口的公共汽车赶往火车站,去家乡看望爷爷.在行驶了三分之一路程后,估计继续乘公共汽车将会在火车开车后半小时到达火车站,便随即下车改乘出租车,车速提高了一倍,结果赶在火车开车前15分钟到达火车站.已知公共汽车的平均速度是40千米/时,问小明家到火车站有多远?练一练 解:设小明家到火车站路程的 为x千米,列方程:解,得
x=60
则小明家到火车站的路程为90千米.答:小明家到火车站的路程为90千米.1.解一元一次方程的步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项,化为最简方程ax=b(a≠0)的形式;
(5)系数化为1.2. 用一元一次方程解决实际问题方面.课堂小结 1.某工厂今年3月份的产量是50万元,5月份上升到72万元,设这两个月的平均增长率为x,则( )
A.50(1+x) =72
B.50(1+x) +50(1+x)2=72
C.50(1+x)x2=72
D.50(1+x)2=72D随堂练习 2.甲、乙二人按2:5的比例投资开办了一家公司,约定除去各项开支外,所得利润投资比例分成,若第一年赢得1400元,那么甲、乙二人分别应分得( )
A.2000元和5000元
B.5000元和2000元
C.4000元和10000元
D.10000元和4000元C3.解下列方程:x=2x=-324.讨论关于x的方程ax=b,的情况. 5.已知2x+1与-12x+5的值是相反数,求x的值.解:根据题意得:
(2x+1)+(-12x+5)=0
去括号,得
2x+1-12x+5=0
称项,得
2x-12x=-1-5
合并同类项,得
-10x=-6
系数化为1,得
x=0.6
答:x的值为0.6.解:根据题意,得解,得6.习题答案
