数学人教A版(2019)必修第一册1.1集合的概念 课件(共22张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册1.1集合的概念 课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
集合的概念
人教A版.必修一
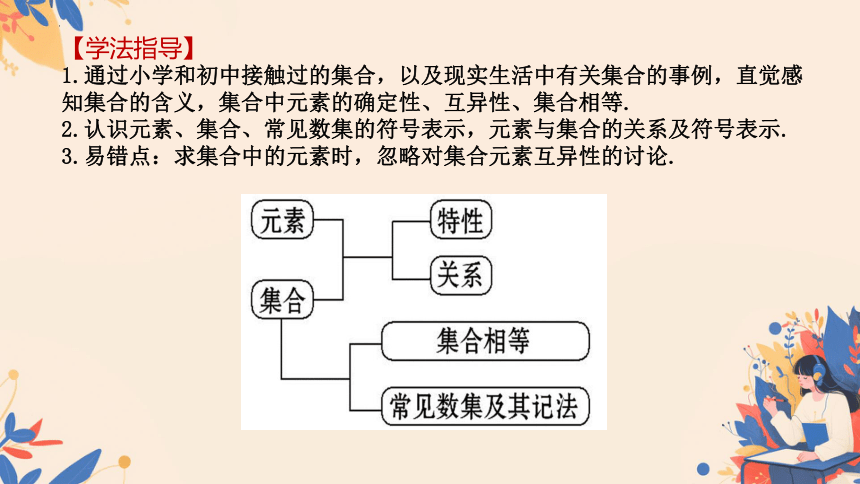
【学法指导】
1.通过小学和初中接触过的集合,以及现实生活中有关集合的事例,直觉感知集合的含义,集合中元素的确定性、互异性、集合相等.
2.认识元素、集合、常见数集的符号表示,元素与集合的关系及符号表示.
3.易错点:求集合中的元素时,忽略对集合元素互异性的讨论.
基 础 学 习
1.集合的概念
观察下列实例,回答下面的问题:
质数又称素数.一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数叫做质数;否则称为合数.
质数(prime number)有无限个.
链接:质数——百度百科
50以内的质数:
2、3、5、7、11、13、17、19、23、29、31、37、41、43、47.
[知识链接]
1.上述实例中的研究对象各是什么 这些研究对象都是确定的吗
例(1)中,我们把1—20以内的每一个素数作为元素,这些元素的全体就是一个集合;例(2)中,把我国从1991~2003年的13年内发射的每一颗人造卫星作为元素,这些元素的全体也是一个集合.
[思考]
提示:例(1)(2)中它们的研究对象分别是素数、每一颗人造卫星.实例中的研究对象都是确定的.
1.集合的有关概念
集合按元素个数分类,可分为:
(1)无限集;
(2)有限集;
(3)空集.
2. 集合的分类
集合论
[拓展阅读]
康托尔
希尔伯特
罗素
[练]1.在“①高一数学课本中的难题;②所有的正三角形;③方程x2+2=0的实数解”中,能够表示成集合的是( )
A.② B.③ C.②③ D.①②③
解析:选C.根据集合的确定性、无序性和互异性,②③具有这三个特点,故能表示成集合,而①中元素不具有确定性,因而不能表示成集合.
2.方程x2=1的解组成的集合为A,则下列各式正确的是( )
A.0∈A B.1 A C.-1∈A D.±1=A
解析:选C.由x2=1,得x=±1,所以集合A中含有元素-1,1.由元素与集合的关系可知-1∈A.
要判断一个元素是否是一个集合的元素,只需看这个元素是否具有这个集合中元素的特性.
①确定性.
②互异性.
③无序性.
[解题方法]
如何判断一个元素是否是一个集合的元素
解析:若a-3=-3,则a=0,此时集合A中的两个元素为-3,-1满足题意.
若2a-1=-3,则a=-1,此时集合A中的两个元素为-4,-3,满足题意.综上可知:a=0或-1.
答案:0或-1
3. 常用数集及其记法
[知识链接]
》实数分类
题 型 探 究
解析:选C.由题意知,a∈A且4-a∈A,a∈N,
若a=0,则4-a=4,A中含元素0,4,满足题意;
若a=1,则4-a=3,A中含元素1,3,满足题意;
若a=2,则4-a=2,A中含元素2,满足题意.
综上,符合要求的集合A有3个.
题型1 元素与集合的关系
【方法总结】判断元素和集合关系的两种方法
①直接法:判断该元素在已知集合中是否出现即可.
②推理法:判断该元素是否满足集合中元素所具有的特征即可.
【方法总结】判断元素与集合关系的两个步骤
(1)确定集合中元素的特征及范围.
(2)判断给定元素是否具有已知集合中元素的特征及是否在限定的范围内.
【例2】已知集合A中含有两个元素a和a2,若1∈A,求实数a的值.
【解题指南】根据1∈A,可得a=1或a2=1,再根据集合中元素的互异性进行检验.
解:因为1∈A,所以a=1或a2=1,即a=±1.
当a=1时,a=a2,集合A中有一个元素,所以a≠1;
当a=-1时,集合A中含有两个元素1,-1,符合互异性,
所以a=-1.
题型2 集合中元素特性的应用
【变换1】本例若去掉条件“1∈A”,其他条件不变,则实数a的取值范围是什么
解:由题意a和a2组成两个元素的集合,则a≠a2,解得a≠0且a≠1.
【方法】根据集合中元素的特性求解字母取值(范围)的三个步骤:
1.知识归纳
课堂小结
2.方法总结
(1)判断元素和集合关系的两种方法
①直接法:判断该元素在已知集合中是否出现即可.
②推理法:判断该元素是否满足集合中元素所具有的特征即可.
(2)根据集合中元素的特性求解字母取值(范围)的三个步骤:
集合的概念
人教A版.必修一
【学法指导】
1.通过小学和初中接触过的集合,以及现实生活中有关集合的事例,直觉感知集合的含义,集合中元素的确定性、互异性、集合相等.
2.认识元素、集合、常见数集的符号表示,元素与集合的关系及符号表示.
3.易错点:求集合中的元素时,忽略对集合元素互异性的讨论.
基 础 学 习
1.集合的概念
观察下列实例,回答下面的问题:
质数又称素数.一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数叫做质数;否则称为合数.
质数(prime number)有无限个.
链接:质数——百度百科
50以内的质数:
2、3、5、7、11、13、17、19、23、29、31、37、41、43、47.
[知识链接]
1.上述实例中的研究对象各是什么 这些研究对象都是确定的吗
例(1)中,我们把1—20以内的每一个素数作为元素,这些元素的全体就是一个集合;例(2)中,把我国从1991~2003年的13年内发射的每一颗人造卫星作为元素,这些元素的全体也是一个集合.
[思考]
提示:例(1)(2)中它们的研究对象分别是素数、每一颗人造卫星.实例中的研究对象都是确定的.
1.集合的有关概念
集合按元素个数分类,可分为:
(1)无限集;
(2)有限集;
(3)空集.
2. 集合的分类
集合论
[拓展阅读]
康托尔
希尔伯特
罗素
[练]1.在“①高一数学课本中的难题;②所有的正三角形;③方程x2+2=0的实数解”中,能够表示成集合的是( )
A.② B.③ C.②③ D.①②③
解析:选C.根据集合的确定性、无序性和互异性,②③具有这三个特点,故能表示成集合,而①中元素不具有确定性,因而不能表示成集合.
2.方程x2=1的解组成的集合为A,则下列各式正确的是( )
A.0∈A B.1 A C.-1∈A D.±1=A
解析:选C.由x2=1,得x=±1,所以集合A中含有元素-1,1.由元素与集合的关系可知-1∈A.
要判断一个元素是否是一个集合的元素,只需看这个元素是否具有这个集合中元素的特性.
①确定性.
②互异性.
③无序性.
[解题方法]
如何判断一个元素是否是一个集合的元素
解析:若a-3=-3,则a=0,此时集合A中的两个元素为-3,-1满足题意.
若2a-1=-3,则a=-1,此时集合A中的两个元素为-4,-3,满足题意.综上可知:a=0或-1.
答案:0或-1
3. 常用数集及其记法
[知识链接]
》实数分类
题 型 探 究
解析:选C.由题意知,a∈A且4-a∈A,a∈N,
若a=0,则4-a=4,A中含元素0,4,满足题意;
若a=1,则4-a=3,A中含元素1,3,满足题意;
若a=2,则4-a=2,A中含元素2,满足题意.
综上,符合要求的集合A有3个.
题型1 元素与集合的关系
【方法总结】判断元素和集合关系的两种方法
①直接法:判断该元素在已知集合中是否出现即可.
②推理法:判断该元素是否满足集合中元素所具有的特征即可.
【方法总结】判断元素与集合关系的两个步骤
(1)确定集合中元素的特征及范围.
(2)判断给定元素是否具有已知集合中元素的特征及是否在限定的范围内.
【例2】已知集合A中含有两个元素a和a2,若1∈A,求实数a的值.
【解题指南】根据1∈A,可得a=1或a2=1,再根据集合中元素的互异性进行检验.
解:因为1∈A,所以a=1或a2=1,即a=±1.
当a=1时,a=a2,集合A中有一个元素,所以a≠1;
当a=-1时,集合A中含有两个元素1,-1,符合互异性,
所以a=-1.
题型2 集合中元素特性的应用
【变换1】本例若去掉条件“1∈A”,其他条件不变,则实数a的取值范围是什么
解:由题意a和a2组成两个元素的集合,则a≠a2,解得a≠0且a≠1.
【方法】根据集合中元素的特性求解字母取值(范围)的三个步骤:
1.知识归纳
课堂小结
2.方法总结
(1)判断元素和集合关系的两种方法
①直接法:判断该元素在已知集合中是否出现即可.
②推理法:判断该元素是否满足集合中元素所具有的特征即可.
(2)根据集合中元素的特性求解字母取值(范围)的三个步骤:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
