4.2 课时3 等差数列的前n项和公式 学案(含答案) 2023-2024学年高二数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.2 课时3 等差数列的前n项和公式 学案(含答案) 2023-2024学年高二数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 159.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览

文档简介
等差数列的前n项和公式
学习目标 1.探索并推导出等差数列前n项和公式 2.理解等差数列前n项公式的特点并解决相关问题.
学习活动
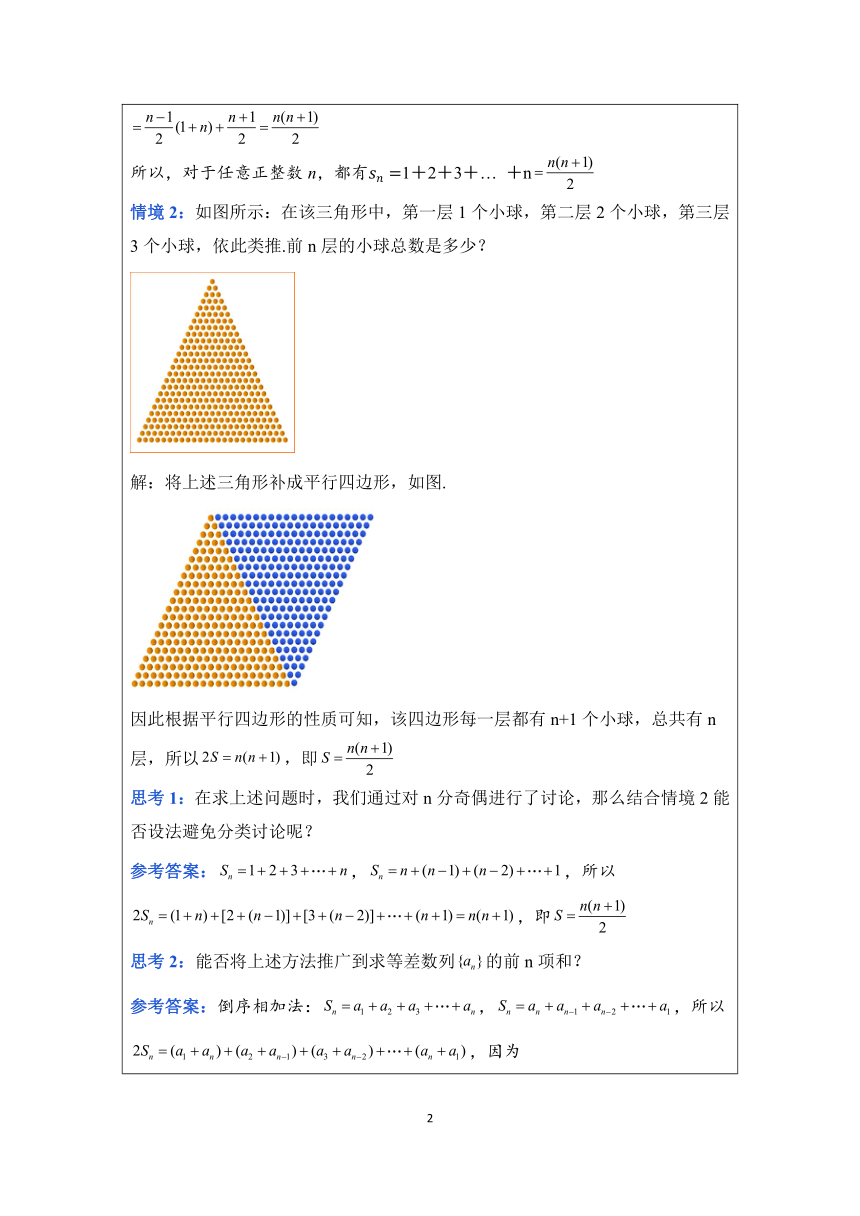
目标一:探索并推导出等差数列前n项和公式. 任务1:根据材料,探索等差数列前n项和公式推导方法. 情境1:据说200多年前,高斯的算术老师提出了下面的问题: 1+2+3+…+100=?当其他同学忙于把100个数逐项相加时,10岁的高斯却 用下面的方法迅速算出了正确答案: (1+100)+(2+99)+…+(50+51)= 高斯的算法实际上解决了求等差数列:1,2,3,…,①前100项的和问题 问题1:高斯在求和过程中利用了数列①的什么性质? 参考答案:等差数列中,. 问题2:如何用高斯的方法求1+2+3+…+100+101=? 参考答案:原式 . 问题3:如何求数列①的前n项和? 参考答案:当n为偶数时, 于是有 当n为奇数时, 有 所以,对于任意正整数n,都有1+2+3+… +n 情境2:如图所示:在该三角形中,第一层1个小球,第二层2个小球,第三层3个小球,依此类推.前n层的小球总数是多少? 解:将上述三角形补成平行四边形,如图. 因此根据平行四边形的性质可知,该四边形每一层都有n+1个小球,总共有n层,所以,即 思考1:在求上述问题时,我们通过对n分奇偶进行了讨论,那么结合情境2能否设法避免分类讨论呢? 参考答案:,,所以,即 思考2:能否将上述方法推广到求等差数列的前n项和? 参考答案:倒序相加法:,,所以,因为,所以,即. 【归纳总结】 等差数列前n项和公式1: 注:其中是等差数列前n项的平均数. 思考3:等差数列前n项和能否用,来表示呢? 参考答案:方法1:将代入前n项和公式,可得; 方法2: . 【归纳总结】 等差数列前n项和公式2:. 练一练: 在等差数列{an}中,S10=120,那么a1+a10的值是( ) A.12 B.24 C.36 D.48 参考答案:解:S10==5(a1+a10)=120, ∴a1+a10=24.故选B.
目标二:理解等差数列前n项公式的特点并解决相关问题. 任务:利用等差数列前n项公式解决与之相关的问题. 例1.已知数列{}是等差数列. (1)若=7, =101,求; (2)若=2, = ,求; (3)若=,d=, =5,求; 参考答案:解:(1)因为=7, =101,根据公式,可得=2700. (2)因为=2, = , 所以d= .根据公式 ,可得 = (3)把=,d= , = 5代入 ,得 整理,得 解得或(舍),所以 思考4:如何合理选择公式1、2解决等差数列的前n项和问题? 【归纳总结】 等差数列的前n项和公式的应用: 1.(1)当已知首项、末项和项数时,可采用公式一;(2)当已知首项、公差和项数时,可采用公式二. 2.两个公式共涉及、、、及五个基本量,知三求二. 例2.已知一个等差数列 前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗? 参考答案:解=310, =1220, 把它们代入公式 得 解方程组,得 所以,由所给的条件可以确定等差数列的首项和公差. 思考5:上述题目如果只知道其中一个条件,能确定这个等差数列吗? 【归纳总结】 一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定. 练一练: 已知等差数列{an}中,a1=1,an=-512,Sn=-1 022,求d. 参考答案:解:由Sn===-1 022, 解之得n=4.又由an=a1+(n-1)d,即-512=1+(4-1)d,解之得d=-171.
学习总结
任务:回答下列关问题,构建知识导图. “倒序相加法”、“等差数列前n项和公式” 参考答案:
2
学习目标 1.探索并推导出等差数列前n项和公式 2.理解等差数列前n项公式的特点并解决相关问题.
学习活动
目标一:探索并推导出等差数列前n项和公式. 任务1:根据材料,探索等差数列前n项和公式推导方法. 情境1:据说200多年前,高斯的算术老师提出了下面的问题: 1+2+3+…+100=?当其他同学忙于把100个数逐项相加时,10岁的高斯却 用下面的方法迅速算出了正确答案: (1+100)+(2+99)+…+(50+51)= 高斯的算法实际上解决了求等差数列:1,2,3,…,①前100项的和问题 问题1:高斯在求和过程中利用了数列①的什么性质? 参考答案:等差数列中,. 问题2:如何用高斯的方法求1+2+3+…+100+101=? 参考答案:原式 . 问题3:如何求数列①的前n项和? 参考答案:当n为偶数时, 于是有 当n为奇数时, 有 所以,对于任意正整数n,都有1+2+3+… +n 情境2:如图所示:在该三角形中,第一层1个小球,第二层2个小球,第三层3个小球,依此类推.前n层的小球总数是多少? 解:将上述三角形补成平行四边形,如图. 因此根据平行四边形的性质可知,该四边形每一层都有n+1个小球,总共有n层,所以,即 思考1:在求上述问题时,我们通过对n分奇偶进行了讨论,那么结合情境2能否设法避免分类讨论呢? 参考答案:,,所以,即 思考2:能否将上述方法推广到求等差数列的前n项和? 参考答案:倒序相加法:,,所以,因为,所以,即. 【归纳总结】 等差数列前n项和公式1: 注:其中是等差数列前n项的平均数. 思考3:等差数列前n项和能否用,来表示呢? 参考答案:方法1:将代入前n项和公式,可得; 方法2: . 【归纳总结】 等差数列前n项和公式2:. 练一练: 在等差数列{an}中,S10=120,那么a1+a10的值是( ) A.12 B.24 C.36 D.48 参考答案:解:S10==5(a1+a10)=120, ∴a1+a10=24.故选B.
目标二:理解等差数列前n项公式的特点并解决相关问题. 任务:利用等差数列前n项公式解决与之相关的问题. 例1.已知数列{}是等差数列. (1)若=7, =101,求; (2)若=2, = ,求; (3)若=,d=, =5,求; 参考答案:解:(1)因为=7, =101,根据公式,可得=2700. (2)因为=2, = , 所以d= .根据公式 ,可得 = (3)把=,d= , = 5代入 ,得 整理,得 解得或(舍),所以 思考4:如何合理选择公式1、2解决等差数列的前n项和问题? 【归纳总结】 等差数列的前n项和公式的应用: 1.(1)当已知首项、末项和项数时,可采用公式一;(2)当已知首项、公差和项数时,可采用公式二. 2.两个公式共涉及、、、及五个基本量,知三求二. 例2.已知一个等差数列 前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗? 参考答案:解=310, =1220, 把它们代入公式 得 解方程组,得 所以,由所给的条件可以确定等差数列的首项和公差. 思考5:上述题目如果只知道其中一个条件,能确定这个等差数列吗? 【归纳总结】 一般地,对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定. 练一练: 已知等差数列{an}中,a1=1,an=-512,Sn=-1 022,求d. 参考答案:解:由Sn===-1 022, 解之得n=4.又由an=a1+(n-1)d,即-512=1+(4-1)d,解之得d=-171.
学习总结
任务:回答下列关问题,构建知识导图. “倒序相加法”、“等差数列前n项和公式” 参考答案:
2
