4.3.1 课时1 等比数列的概念 学案(表格式,含答案) 2023-2024学年高二数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 4.3.1 课时1 等比数列的概念 学案(表格式,含答案) 2023-2024学年高二数学人教A版(2019)选择性必修第二册 | 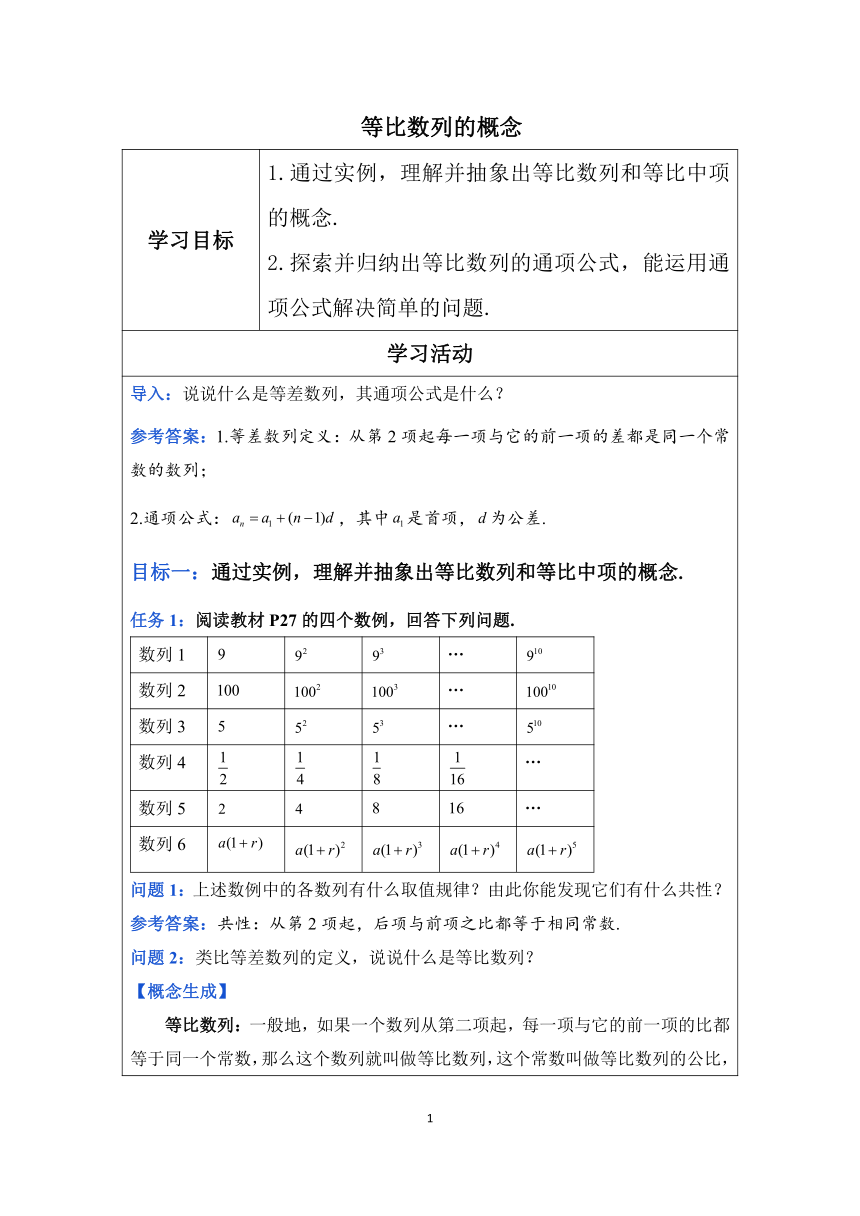 | |
| 格式 | docx | ||
| 文件大小 | 210.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 17:23:05 | ||
图片预览



文档简介
等比数列的概念
学习目标 1.通过实例,理解并抽象出等比数列和等比中项的概念. 2.探索并归纳出等比数列的通项公式,能运用通项公式解决简单的问题.
学习活动
导入:说说什么是等差数列,其通项公式是什么? 参考答案:1.等差数列定义:从第2项起每一项与它的前一项的差都是同一个常数的数列; 2.通项公式:,其中是首项,为公差. 目标一:通过实例,理解并抽象出等比数列和等比中项的概念. 任务1:阅读教材P27的四个数例,回答下列问题. 数列1…数列2…数列3…数列4…数列5…数列6
问题1:上述数例中的各数列有什么取值规律?由此你能发现它们有什么共性? 参考答案:共性:从第2项起,后项与前项之比都等于相同常数. 问题2:类比等差数列的定义,说说什么是等比数列? 【概念生成】 等比数列:一般地,如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示. 符号表示:. 注:(1)等比数列各项不能为0;(2)数列任意前后两项之比为定值. 练一练: 观察并判断下列数列是否是等比数列,若是,说出公比;若不是,说明理由. 2, 4, 16, 64, … 不是,前后两项之比不同; (2) 5,-5,5,-5, … 是,; (3) 1,0,1,0,… 不是,不能等于0; (4) … 不是,当时,不满足. 问题3:在如下的两个数之间插入一个什么数后,得到的三个数会成为一个等比数列: (1)1,( ), 9; (2)-1,( ),-4 参考答案:;. 问题4:类比等差中项的概念,说说什么是等比中项? 【概念讲解】 等比中项:如果在与中间插入一个数G,使成等比数列,那么G叫做与的等比中项. 根据等比数列的定义,可以推出 思考: 任何两个非零实数都有等比中项吗? 【归纳总结】 同号的两数的等比中项有两个,它们互为相反数;异号的两数没有等比中项.
目标二:探索并归纳出等比数列的通项公式,能运用通项公式解决简单的问题. 任务1:类比等差数列通项公式推导方法推导等比数列同学公式. 问题1:我们知道等比数列满足:,由此如何类比等差数列通项公式的推导推导等比数列通项公式? 参考答案:法1:(不完全归纳法)设一个等比数列的公比为.根据等比数列的定义,可得,所以 …… . 又,即当n=1时上式也成立.因此,首项为,公比为q的等比数列的通项公式为 法2:(累乘法)设一个等比数列的公比为.根据等比数列的定义,可得,则 将以上(n-1)个式子相乘,得 又,这就是说,当n=1时上式也成立.因此,首项为,公比为q的等比数列的通项公式为 由此我们便得到了等比数列的通项公式: 【归纳总结】 等比数列通项公式:,其中首项为,公比为q. 任务2:利用等比数列通项公式求解有关等比数列问题. 例1:若等比数列的第4项和第6项分别为48和12,求的第5项. 问题1:该题目已知条件有几个,如何利用等比数列通项公式求解? 参考答案:两个,分别是已知等比数列的第4项和第6项的值.解:由,,得,②的两边分别除以①的两边,得.解得. 把代入①,得.此时,把代入①,得.此时 .因此,的第5项是24或-24. 思考:利用等比数列通项公式求解等比数列问题时,需要已知多少条件? 【归纳总结】 只要给定两个独立的条件,就能确定等比数列,从而求出数列的某一项. 问题2:除了上述利用等比数列通项公式求解,还有没有其他办法? 参考答案:解:因为是与的等比中项,所以.所以.因此,的第5项是24或-24. 例2:已知等比数列的公比为, 试用的第项表示. 参考答案:解:由题意,得,① . ②的两边分别除以①的两边,得= 所以 . 【归纳总结】 等比数列的任意一项,都可以有该数列的某一项和公比表示,即. 例3:数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132,求这个数列. 问题1.如何设这个数列未知项会使得列式比较简单? 参考答案:因为已知条件是说前三项成等比数列,后三项成等差数列,第3项等于80,因此以第三项为基础,设等比数列的公比为q,等差数列的公差为d,所以数列的各项依次为 ,80,80, 80. 问题2.求该数列的各项. 参考答案:由问题1可列式:,解得 所以这个数列是20,40,80,96,112,或180,120,80,16,-48. 练一练: 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数. 参考答案:解:法1:设这四个数依次为, 于是得解方程组,得 所以当a=4,d=4时,所求的四个数为0,4,8,16; 当a=9,d=-6时,所求的四个数为15,9,3,1. 故所求的四个数为0,4,8,16或15,9,3,1. 法2:设这四个数依次为, 于是得解方程组,得 所以当a=8,q=2时,所求的四个数为0,4,8,16; 当a=3,时,所求的四个数为15,9,3,1. 故所求的四个数为0,4,8,16或15,9,3,1.
学习总结
任务:回答下列关问题,构建知识导图. “定义”、“通项公式”、“等比中项” 参考答案:
2
学习目标 1.通过实例,理解并抽象出等比数列和等比中项的概念. 2.探索并归纳出等比数列的通项公式,能运用通项公式解决简单的问题.
学习活动
导入:说说什么是等差数列,其通项公式是什么? 参考答案:1.等差数列定义:从第2项起每一项与它的前一项的差都是同一个常数的数列; 2.通项公式:,其中是首项,为公差. 目标一:通过实例,理解并抽象出等比数列和等比中项的概念. 任务1:阅读教材P27的四个数例,回答下列问题. 数列1…数列2…数列3…数列4…数列5…数列6
问题1:上述数例中的各数列有什么取值规律?由此你能发现它们有什么共性? 参考答案:共性:从第2项起,后项与前项之比都等于相同常数. 问题2:类比等差数列的定义,说说什么是等比数列? 【概念生成】 等比数列:一般地,如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示. 符号表示:. 注:(1)等比数列各项不能为0;(2)数列任意前后两项之比为定值. 练一练: 观察并判断下列数列是否是等比数列,若是,说出公比;若不是,说明理由. 2, 4, 16, 64, … 不是,前后两项之比不同; (2) 5,-5,5,-5, … 是,; (3) 1,0,1,0,… 不是,不能等于0; (4) … 不是,当时,不满足. 问题3:在如下的两个数之间插入一个什么数后,得到的三个数会成为一个等比数列: (1)1,( ), 9; (2)-1,( ),-4 参考答案:;. 问题4:类比等差中项的概念,说说什么是等比中项? 【概念讲解】 等比中项:如果在与中间插入一个数G,使成等比数列,那么G叫做与的等比中项. 根据等比数列的定义,可以推出 思考: 任何两个非零实数都有等比中项吗? 【归纳总结】 同号的两数的等比中项有两个,它们互为相反数;异号的两数没有等比中项.
目标二:探索并归纳出等比数列的通项公式,能运用通项公式解决简单的问题. 任务1:类比等差数列通项公式推导方法推导等比数列同学公式. 问题1:我们知道等比数列满足:,由此如何类比等差数列通项公式的推导推导等比数列通项公式? 参考答案:法1:(不完全归纳法)设一个等比数列的公比为.根据等比数列的定义,可得,所以 …… . 又,即当n=1时上式也成立.因此,首项为,公比为q的等比数列的通项公式为 法2:(累乘法)设一个等比数列的公比为.根据等比数列的定义,可得,则 将以上(n-1)个式子相乘,得 又,这就是说,当n=1时上式也成立.因此,首项为,公比为q的等比数列的通项公式为 由此我们便得到了等比数列的通项公式: 【归纳总结】 等比数列通项公式:,其中首项为,公比为q. 任务2:利用等比数列通项公式求解有关等比数列问题. 例1:若等比数列的第4项和第6项分别为48和12,求的第5项. 问题1:该题目已知条件有几个,如何利用等比数列通项公式求解? 参考答案:两个,分别是已知等比数列的第4项和第6项的值.解:由,,得,②的两边分别除以①的两边,得.解得. 把代入①,得.此时,把代入①,得.此时 .因此,的第5项是24或-24. 思考:利用等比数列通项公式求解等比数列问题时,需要已知多少条件? 【归纳总结】 只要给定两个独立的条件,就能确定等比数列,从而求出数列的某一项. 问题2:除了上述利用等比数列通项公式求解,还有没有其他办法? 参考答案:解:因为是与的等比中项,所以.所以.因此,的第5项是24或-24. 例2:已知等比数列的公比为, 试用的第项表示. 参考答案:解:由题意,得,① . ②的两边分别除以①的两边,得= 所以 . 【归纳总结】 等比数列的任意一项,都可以有该数列的某一项和公比表示,即. 例3:数列共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132,求这个数列. 问题1.如何设这个数列未知项会使得列式比较简单? 参考答案:因为已知条件是说前三项成等比数列,后三项成等差数列,第3项等于80,因此以第三项为基础,设等比数列的公比为q,等差数列的公差为d,所以数列的各项依次为 ,80,80, 80. 问题2.求该数列的各项. 参考答案:由问题1可列式:,解得 所以这个数列是20,40,80,96,112,或180,120,80,16,-48. 练一练: 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数. 参考答案:解:法1:设这四个数依次为, 于是得解方程组,得 所以当a=4,d=4时,所求的四个数为0,4,8,16; 当a=9,d=-6时,所求的四个数为15,9,3,1. 故所求的四个数为0,4,8,16或15,9,3,1. 法2:设这四个数依次为, 于是得解方程组,得 所以当a=8,q=2时,所求的四个数为0,4,8,16; 当a=3,时,所求的四个数为15,9,3,1. 故所求的四个数为0,4,8,16或15,9,3,1.
学习总结
任务:回答下列关问题,构建知识导图. “定义”、“通项公式”、“等比中项” 参考答案:
2
