5.1.1 课时2 变化率问题 学案(表格式,含答案) 2023-2024学年高二数学人教A版(2019)选择性必修第二册
文档属性
| 名称 | 5.1.1 课时2 变化率问题 学案(表格式,含答案) 2023-2024学年高二数学人教A版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 457.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 17:22:56 | ||
图片预览

文档简介
课时2 变化率问题
学习目标 1.能通过极限思想理解抛物线切线与割线的斜率的关系,并能求曲线切线的斜率.
学习活动
导入:我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切,那么对于一般的曲线C,如何定义它的切线呢? 目标:能通过极限思想理解抛物线切线与割线的斜率,并能求曲线切线的斜率. 任务1:研究抛物线在点处的切线. 问题1:观察抛物线在点处的切线图象,说说你如何定义它的切线? 问题2:在点附近任取一点,观察下面动图,说说曲线的割线与切线有怎样的关系? 参考答案:当点时,割线切线PT,当P点与重合时,割线与切线PT重合. 问题3:记,则点P的坐标为,割线的斜率的表达式是什么? 参考答案:. 问题4:观察下表,当,即时,割线的斜率变化趋势是怎样的?据此思考如何求出切线的斜率? …………
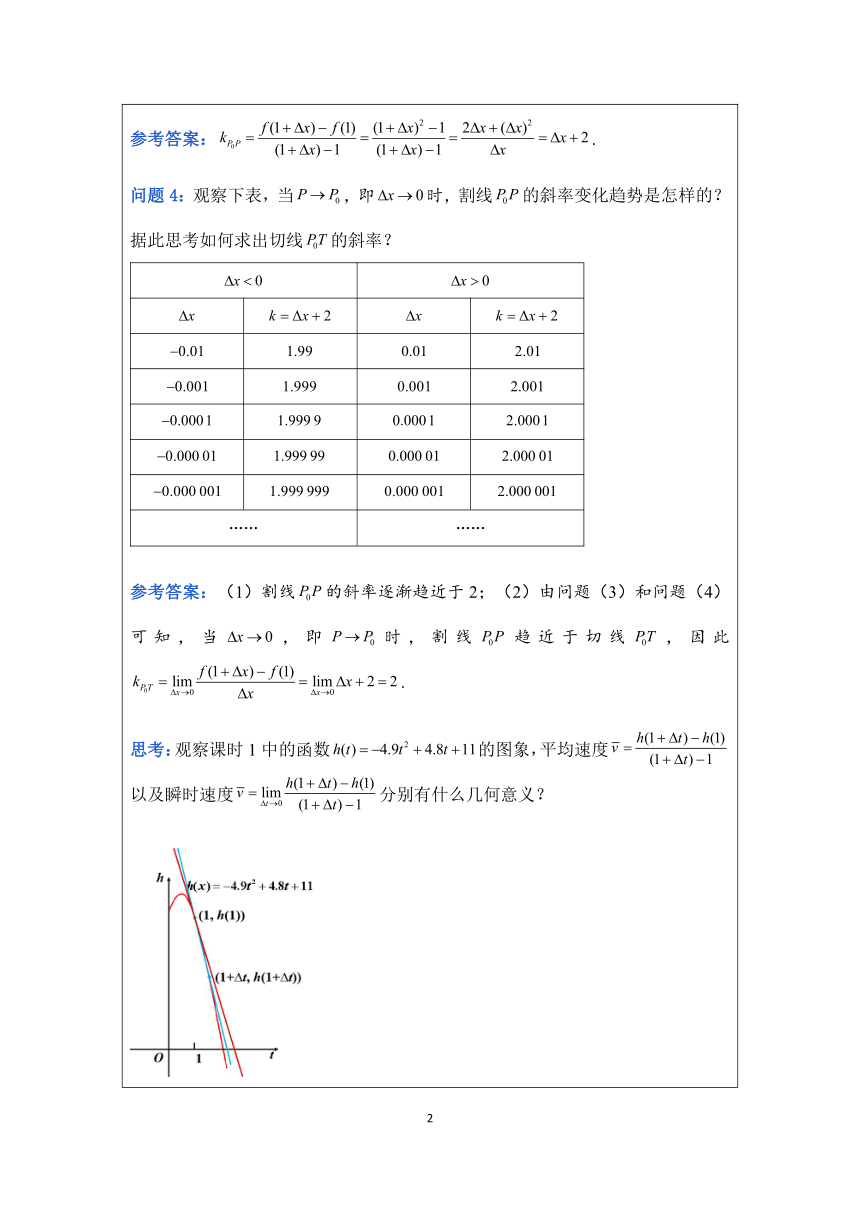
参考答案:(1)割线的斜率逐渐趋近于2;(2)由问题(3)和问题(4)可知,当,即时,割线趋近于切线,因此. 思考:观察课时1中的函数的图象,平均速度以及瞬时速度分别有什么几何意义? 参考答案:(1)平均速度的几何意义:过点,的割线的斜率.(2)瞬时速度的几何意义:表示函数在点处的切线斜率. 【归纳总结】 抛物线的割线及切线斜率: 1.割线斜率:; 2.切线斜率:. 任务2:求抛物线在某点处的切线的斜率及方程. 已知抛物线,求其在点(0,1)处的切线的斜率及方程. 参考答案:解:(1)设切线的斜率为k,则 . (2)切线过点(0,1),所以切线方程为,即. 【归纳总结】 曲线在某点处的切线的斜率:;切线方程:. 练一练: 已知抛物线,求其在点(﹣1,1)处的切线方程. 参考答案:解:设切线的斜率为k,则 . 又切线过点(﹣1,1),所以切线方程为,即.
学习总结
任务:根据下列关键词,构建知识导图. “割线斜率”、“极限思想”、“切线斜率”、“切线方程”. 参考答案:
2
学习目标 1.能通过极限思想理解抛物线切线与割线的斜率的关系,并能求曲线切线的斜率.
学习活动
导入:我们知道,如果一条直线与一个圆只有一个公共点,那么这条直线与这个圆相切,那么对于一般的曲线C,如何定义它的切线呢? 目标:能通过极限思想理解抛物线切线与割线的斜率,并能求曲线切线的斜率. 任务1:研究抛物线在点处的切线. 问题1:观察抛物线在点处的切线图象,说说你如何定义它的切线? 问题2:在点附近任取一点,观察下面动图,说说曲线的割线与切线有怎样的关系? 参考答案:当点时,割线切线PT,当P点与重合时,割线与切线PT重合. 问题3:记,则点P的坐标为,割线的斜率的表达式是什么? 参考答案:. 问题4:观察下表,当,即时,割线的斜率变化趋势是怎样的?据此思考如何求出切线的斜率? …………
参考答案:(1)割线的斜率逐渐趋近于2;(2)由问题(3)和问题(4)可知,当,即时,割线趋近于切线,因此. 思考:观察课时1中的函数的图象,平均速度以及瞬时速度分别有什么几何意义? 参考答案:(1)平均速度的几何意义:过点,的割线的斜率.(2)瞬时速度的几何意义:表示函数在点处的切线斜率. 【归纳总结】 抛物线的割线及切线斜率: 1.割线斜率:; 2.切线斜率:. 任务2:求抛物线在某点处的切线的斜率及方程. 已知抛物线,求其在点(0,1)处的切线的斜率及方程. 参考答案:解:(1)设切线的斜率为k,则 . (2)切线过点(0,1),所以切线方程为,即. 【归纳总结】 曲线在某点处的切线的斜率:;切线方程:. 练一练: 已知抛物线,求其在点(﹣1,1)处的切线方程. 参考答案:解:设切线的斜率为k,则 . 又切线过点(﹣1,1),所以切线方程为,即.
学习总结
任务:根据下列关键词,构建知识导图. “割线斜率”、“极限思想”、“切线斜率”、“切线方程”. 参考答案:
2
