物理人教版(2019)选择性必修第一册2.3简谐运动的回复力和能量(共16张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册2.3简谐运动的回复力和能量(共16张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 585.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-02 11:48:59 | ||
图片预览





文档简介
(共16张PPT)
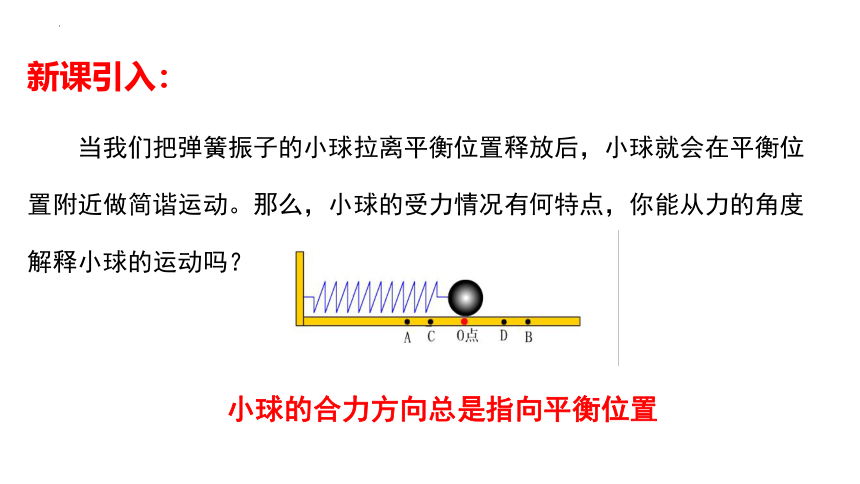
新课引入:
当我们把弹簧振子的小球拉离平衡位置释放后,小球就会在平衡位置附近做简谐运动。那么,小球的受力情况有何特点,你能从力的角度解释小球的运动吗?
小球的合力方向总是指向平衡位置
一、简谐运动的回复力:
1、定义:使振子回到平衡位置的力
思考与讨论:
回复力是不是物体新受到的一种力?
你认为回复力是什么力来提供的呢?
你能根据弹簧振子分析出回复力和偏离平衡位置位移大小的关系吗?
公式中的k是弹簧的劲度系数吗?
你能从力的角度给简谐运动下个定义吗?
若要判断一个物体是否做简谐运动,你认为有哪些方法?
2、来源:回复力是一种效果力,可以是某一个力,也可以是几个力的合力,或者某个力的分力
3、方向:始终指向平衡位置
4、大小:F=-kx
“-” 表示回复力方向始终与位移方向相反.
k不一定是劲度系数而是回复力与位移的比例系数
5、简谐运动的力学特征:如果物体在运动方向上所受的力与它偏离平衡位置的位移大小成正比,并且始终指向平衡位置(即与位移方向相反),质点的运动就是简谐运动。
典例:如图,一弹簧上端固定,劲度系数为k,另一端挂一质量为m的小球,平衡位置时弹簧的形变量为x0,释放后小球做上下运动,弹簧此时没有超出弹性限度,小球的运动是简谐运动吗?其回复力是谁提供的?
证明:规定向下为正方向
平衡位置时弹簧的形变量为x0, 则 mg=kx0
当小球向下运动到离平衡位置的距离是x时,
回复力:F=mg-k(x0+x) 得F=-kx,即小球的运动是简谐运动。
重力和弹力的合力提供回复力
x0
o
二、简谐运动的能量:
思考与讨论:
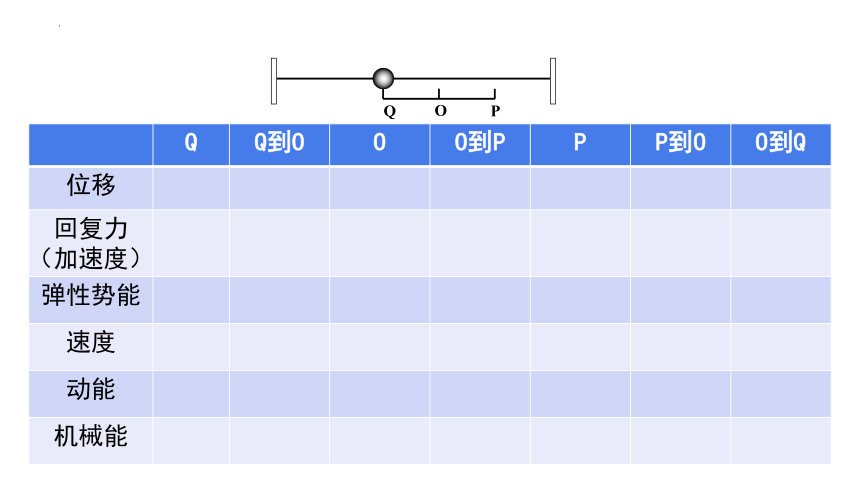
通过对弹簧振子所做简谐运动的学习,我们知道,弹簧振子的速度是不断变化的,所以它的动能也是不断变化的;弹簧的伸长量和压缩量也是不断变化的,所以它的弹性势能也是不断变化的。那么弹簧振子的能量变化具有什么规律呢?
Q Q到O O O到P P P到O O到Q
位移
回复力(加速度)
弹性势能
速度
动能
机械能
O
Q
P
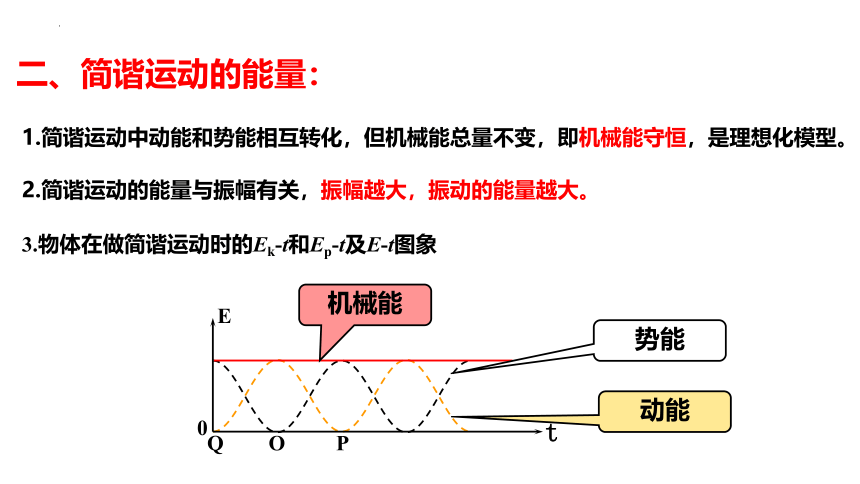
1.简谐运动中动能和势能相互转化,但机械能总量不变,即机械能守恒,是理想化模型。
2.简谐运动的能量与振幅有关,振幅越大,振动的能量越大。
3.物体在做简谐运动时的Ek-t和Ep-t及E-t图象
t
E
0
机械能
势能
动能
Q
P
O
二、简谐运动的能量:
典例:如图甲所示,劲度系数为k的轻弹簧下端挂一质量为m的小球(可视为质点),小球在竖直方向上做简谐运动,弹簧对小球的拉力F随时间变化的图像如图乙所示。已知弹簧弹性势能的表达式为 ,x为弹簧的形变量,重力加速度为g。下列说法正确的是( )
A.小球的振幅为
B.小球的最大加速度为2g
C.小球的最大动能为
D.在振动过程中,弹簧的弹性势能和小球的动能总和不变
【正确答案】C
A
C
C
D
CD
AD
7、如图所示,一劲度系数为k的轻弹簧,下端被固定在水平地面上,上端与质量为m的小球(可视为质点)相连,开始时小球静止于O点。现用一竖直向上的拉力将小球缓慢拉至P点,此时弹簧恢复原长。t=0时刻撤去拉力,小球由静止开始做简谐运动,经时间第一次回到O点,已知弹簧的形变量为x时,弹性势能为 ,重力加速度为g。求:
(1)小球的振幅A;
(2)小球的振动方程(选竖直向上为正方向);
(3)小球振动速度的最大值vm。
新课引入:
当我们把弹簧振子的小球拉离平衡位置释放后,小球就会在平衡位置附近做简谐运动。那么,小球的受力情况有何特点,你能从力的角度解释小球的运动吗?
小球的合力方向总是指向平衡位置
一、简谐运动的回复力:
1、定义:使振子回到平衡位置的力
思考与讨论:
回复力是不是物体新受到的一种力?
你认为回复力是什么力来提供的呢?
你能根据弹簧振子分析出回复力和偏离平衡位置位移大小的关系吗?
公式中的k是弹簧的劲度系数吗?
你能从力的角度给简谐运动下个定义吗?
若要判断一个物体是否做简谐运动,你认为有哪些方法?
2、来源:回复力是一种效果力,可以是某一个力,也可以是几个力的合力,或者某个力的分力
3、方向:始终指向平衡位置
4、大小:F=-kx
“-” 表示回复力方向始终与位移方向相反.
k不一定是劲度系数而是回复力与位移的比例系数
5、简谐运动的力学特征:如果物体在运动方向上所受的力与它偏离平衡位置的位移大小成正比,并且始终指向平衡位置(即与位移方向相反),质点的运动就是简谐运动。
典例:如图,一弹簧上端固定,劲度系数为k,另一端挂一质量为m的小球,平衡位置时弹簧的形变量为x0,释放后小球做上下运动,弹簧此时没有超出弹性限度,小球的运动是简谐运动吗?其回复力是谁提供的?
证明:规定向下为正方向
平衡位置时弹簧的形变量为x0, 则 mg=kx0
当小球向下运动到离平衡位置的距离是x时,
回复力:F=mg-k(x0+x) 得F=-kx,即小球的运动是简谐运动。
重力和弹力的合力提供回复力
x0
o
二、简谐运动的能量:
思考与讨论:
通过对弹簧振子所做简谐运动的学习,我们知道,弹簧振子的速度是不断变化的,所以它的动能也是不断变化的;弹簧的伸长量和压缩量也是不断变化的,所以它的弹性势能也是不断变化的。那么弹簧振子的能量变化具有什么规律呢?
Q Q到O O O到P P P到O O到Q
位移
回复力(加速度)
弹性势能
速度
动能
机械能
O
Q
P
1.简谐运动中动能和势能相互转化,但机械能总量不变,即机械能守恒,是理想化模型。
2.简谐运动的能量与振幅有关,振幅越大,振动的能量越大。
3.物体在做简谐运动时的Ek-t和Ep-t及E-t图象
t
E
0
机械能
势能
动能
Q
P
O
二、简谐运动的能量:
典例:如图甲所示,劲度系数为k的轻弹簧下端挂一质量为m的小球(可视为质点),小球在竖直方向上做简谐运动,弹簧对小球的拉力F随时间变化的图像如图乙所示。已知弹簧弹性势能的表达式为 ,x为弹簧的形变量,重力加速度为g。下列说法正确的是( )
A.小球的振幅为
B.小球的最大加速度为2g
C.小球的最大动能为
D.在振动过程中,弹簧的弹性势能和小球的动能总和不变
【正确答案】C
A
C
C
D
CD
AD
7、如图所示,一劲度系数为k的轻弹簧,下端被固定在水平地面上,上端与质量为m的小球(可视为质点)相连,开始时小球静止于O点。现用一竖直向上的拉力将小球缓慢拉至P点,此时弹簧恢复原长。t=0时刻撤去拉力,小球由静止开始做简谐运动,经时间第一次回到O点,已知弹簧的形变量为x时,弹性势能为 ,重力加速度为g。求:
(1)小球的振幅A;
(2)小球的振动方程(选竖直向上为正方向);
(3)小球振动速度的最大值vm。
