山东省巨野县第一中学人教版数学必修二21空间中直线与直线之间的位置关系 课件(共24张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教版数学必修二21空间中直线与直线之间的位置关系 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 474.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-06 21:24:42 | ||
图片预览






文档简介
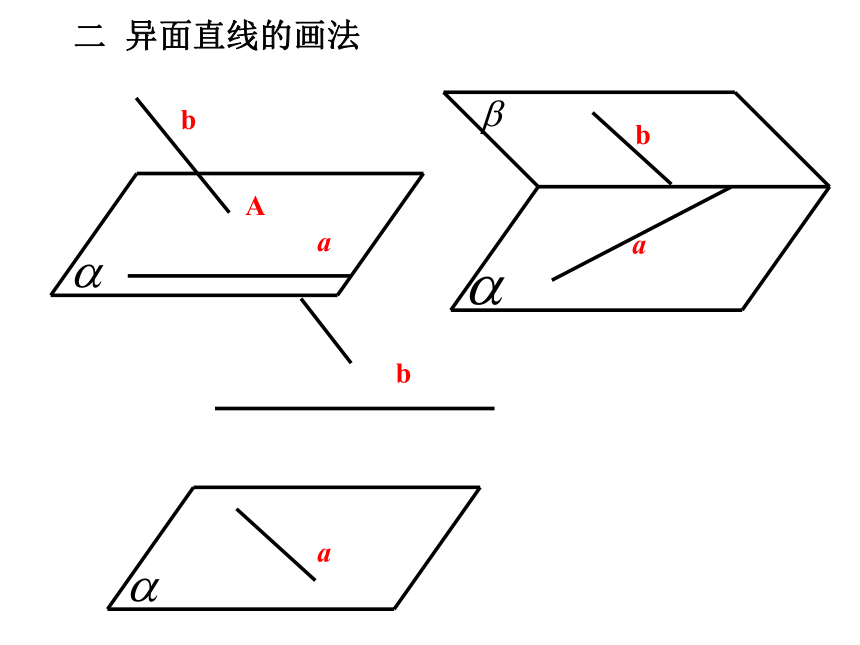
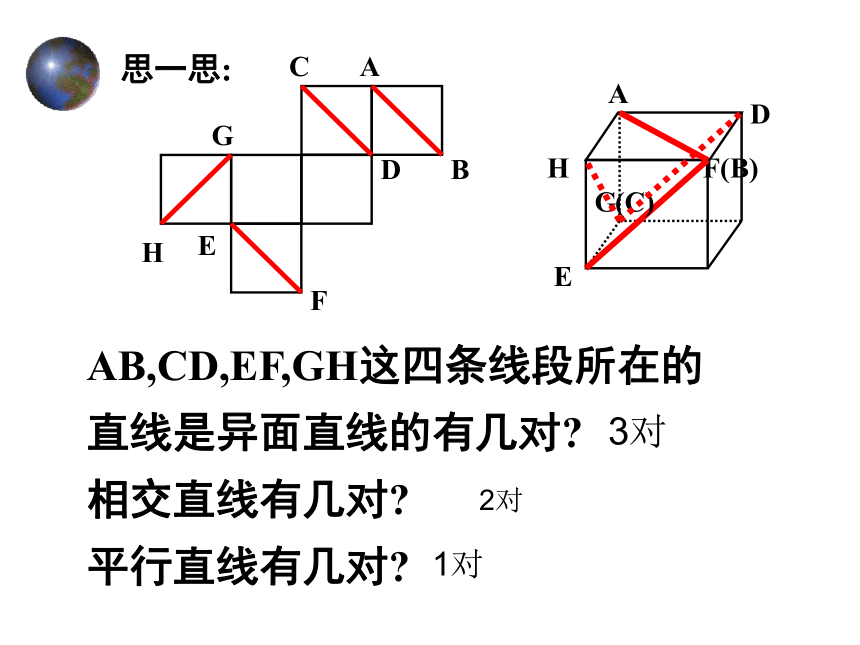
课件24张PPT。2.1.2 空间中直线与直线的位置关系六角螺母定义1:不同在任何一个平面内的两条直线叫做异面直线。注:1 概念应理解为:“经过这两条直线无法作出一个平面” .或:“不可能找到一个平面同时经过这两条直线”.一、异面直线:2.简单地说,异面直线为既不平行也不相交的直线Abababa二 异面直线的画法想一想:在空间中两条直线的位置关系?共面直线相交直线:平行直线:同一平面内,有且只有一个公共点同一平面内,没有公共点异面直线:不同在任何一个平面内,没有公共点空间中两直线的位置关系AB,CD,EF,GH这四条线段所在的直线是异面直线的有几对?
相交直线有几对?
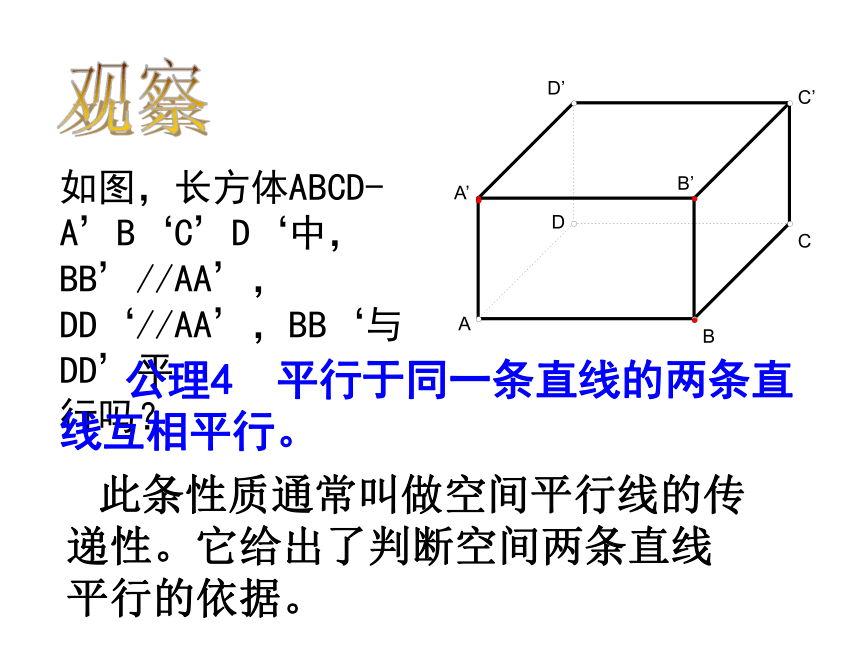
平行直线有几对?3对2对1对练一练:正方体ABCD-A1B1C1D1 的所有棱 中1、与A1A是异面的有:2、与D1B异面的有:BC DC B1C1 D1C1AA1 AD A1B1 B1C1 CC1 CD观察如图,长方体ABCD-A’B‘C’D‘中,BB’//AA’,DD‘//AA’,BB‘与DD’平
行吗? 公理4 平行于同一条直线的两条直线互相平行。 此条性质通常叫做空间平行线的传递性。它给出了判断空间两条直线平行的依据。例1:已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,
求证EFGH是一个平行四边形。解题思想:把所要解的立体几何问题转化为平面几何的问题——解立体几何时最主要、最常用的一种方法。同一平面内:思考2: 如图,四棱柱ABCD--A′B′C′D′ 的底面是平行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何 ?等角定理
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补. 三、异面直线所成角的定义:
已知两条异面直线 a , b , 经过空间任一点O作 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角(或直角)叫做异面直线所成的角(或夹角).O思想方法 : 平移转化成相交直线所成的角,即化空间图形问题为平面图形问题思考 : 这个角的大小与O点的位置有关吗 ? 即O点位置不同时, 这一角的大小是否改变?NEXTBACK 如果两条异面直线所成的角为直角,
那么就称这两条异面直线垂直。异面直线a和b所成的角的范围:45o例2:(1)求直线BA1和CC1所成角的度数。例2:(2)哪些棱所在直线与直线AA1垂直?一作(找)、二证、三求(1)通过直线平移,作出异面直线
所成的角,把空间问题转化为
平面问题。
(2)利用平面几何知识,
求出异面直线所成角的大小。四、异面直线所成角的求法:例3:在正方体ABCD-A’B’C’D’中,棱长为a,
E、F分别是棱A’B’,B’C’的中点,求:①异面直线 AD与 EF所成角的大小;②异面直线 B’C与 EF所成角的大小;③异面直线 B’D与 EF
所成角的大小.平
移
法OGAC∥ A’C’∥ EF, OG ∥B’DB’D 与EF所成的角
即为AC与OG所成的角, 即为∠AOG或其补角.课堂小结作业: P48:1,2问题:在空间中,如果一个角的两边和另一个角的两边分别平行,那么这两个角相等吗?αβ再
见
!立体几何
相交直线有几对?
平行直线有几对?3对2对1对练一练:正方体ABCD-A1B1C1D1 的所有棱 中1、与A1A是异面的有:2、与D1B异面的有:BC DC B1C1 D1C1AA1 AD A1B1 B1C1 CC1 CD观察如图,长方体ABCD-A’B‘C’D‘中,BB’//AA’,DD‘//AA’,BB‘与DD’平
行吗? 公理4 平行于同一条直线的两条直线互相平行。 此条性质通常叫做空间平行线的传递性。它给出了判断空间两条直线平行的依据。例1:已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,
求证EFGH是一个平行四边形。解题思想:把所要解的立体几何问题转化为平面几何的问题——解立体几何时最主要、最常用的一种方法。同一平面内:思考2: 如图,四棱柱ABCD--A′B′C′D′ 的底面是平行四边形,∠ADC与∠A′D′C′, ∠ADC与∠B′A′D′的两边分别对应平行,这两组角的大小关系如何 ?等角定理
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补. 三、异面直线所成角的定义:
已知两条异面直线 a , b , 经过空间任一点O作 直线 a′∥a , b ′∥b 则把 a ′与 b ′所成的锐角(或直角)叫做异面直线所成的角(或夹角).O思想方法 : 平移转化成相交直线所成的角,即化空间图形问题为平面图形问题思考 : 这个角的大小与O点的位置有关吗 ? 即O点位置不同时, 这一角的大小是否改变?NEXTBACK 如果两条异面直线所成的角为直角,
那么就称这两条异面直线垂直。异面直线a和b所成的角的范围:45o例2:(1)求直线BA1和CC1所成角的度数。例2:(2)哪些棱所在直线与直线AA1垂直?一作(找)、二证、三求(1)通过直线平移,作出异面直线
所成的角,把空间问题转化为
平面问题。
(2)利用平面几何知识,
求出异面直线所成角的大小。四、异面直线所成角的求法:例3:在正方体ABCD-A’B’C’D’中,棱长为a,
E、F分别是棱A’B’,B’C’的中点,求:①异面直线 AD与 EF所成角的大小;②异面直线 B’C与 EF所成角的大小;③异面直线 B’D与 EF
所成角的大小.平
移
法OGAC∥ A’C’∥ EF, OG ∥B’DB’D 与EF所成的角
即为AC与OG所成的角, 即为∠AOG或其补角.课堂小结作业: P48:1,2问题:在空间中,如果一个角的两边和另一个角的两边分别平行,那么这两个角相等吗?αβ再
见
!立体几何
