山东省巨野县第一中学人教版数学必修四24平面向量数量积 课件(共24张PPT)
文档属性
| 名称 | 山东省巨野县第一中学人教版数学必修四24平面向量数量积 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 344.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 11:14:13 | ||
图片预览








文档简介
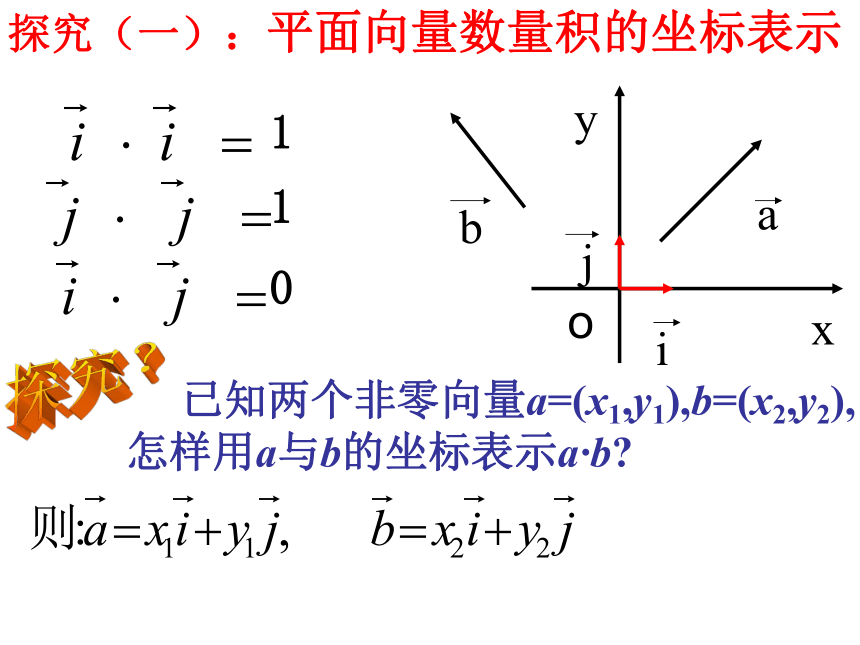
课件24张PPT。2.4.2平面向量数量积的坐标表示、模、夹角一复习引入 2.平面向量的数量积满足的运算律? 平面向量的表示方法有几何法和坐标法,向量的坐标表示,对向量的加、减、数乘运算带来了很大的方便.若已知向量a与b的坐标,则其数量积是唯一确定的,因此,如何用坐标表示向量的数量积就成为我们需要研究的课题. 探究(一):平面向量数量积的坐标表示 oxyabij110 已知两个非零向量a=(x1,y1),b=(x2,y2), 怎样用a与b的坐标表示a·b?探究?两个向量的数量积等于它们对应坐标的乘积的和.练习1:已知向量求:(1)
(2)=(1,-2)探究(二):向量的模和夹角的坐标表示 (1)向量的模(2)设则(3)平行(4)垂直(5)设 是两个非零向量,其夹角为θ,若 那么cosθ如何用坐 标表示? 例题讲解例1:设a=(5,-7),b=(-6,-4),求a·b及a、b间的夹角θ(精确到1°)解a·b = 5×(-6)+(-7) ×(-4)
= -30+28
= -2例2:已知向量则则变式:已知向量 a=(λ,-2),
b=(-3,5),若向量a 与b的夹角为钝角,求λ的取值范围. 例4 已知A(1,2),B(2,3),C(-2,5), 试判断?ABC的形状,并给出证明.思考:还有其他证明方法吗?向量的数量积是否为零,是判断相应的两条线段或直线是否垂直的重要方法之一练习已知a=(λ,2),b=(-3,5),且a和b的夹角是钝角,则λ的范围是[ ]BA练习B练习分析:为求a与b夹角,需先求a·b及|a||b|,再结合夹角θ的范围确定其值. 0≤θ≤π解记a与b的夹角为θ又0≤θ≤π知三角形函数值求角时,应注重角的范围的确定 已知a=(3,4),b=(4,3),求x,y的值使(xa+yb)⊥a,且|xa+yb|=1. 练习小结A、B两点间的距离公式:已知小结2.向量的坐标运算沟通了向量与解析几何的内在联系,解析几何中与角度、距离、平行、垂直有关的问题,可以考虑用向量方法来解决. 作业课本第121页习题2.4A组题6,7,8Thank you!
(2)=(1,-2)探究(二):向量的模和夹角的坐标表示 (1)向量的模(2)设则(3)平行(4)垂直(5)设 是两个非零向量,其夹角为θ,若 那么cosθ如何用坐 标表示? 例题讲解例1:设a=(5,-7),b=(-6,-4),求a·b及a、b间的夹角θ(精确到1°)解a·b = 5×(-6)+(-7) ×(-4)
= -30+28
= -2例2:已知向量则则变式:已知向量 a=(λ,-2),
b=(-3,5),若向量a 与b的夹角为钝角,求λ的取值范围. 例4 已知A(1,2),B(2,3),C(-2,5), 试判断?ABC的形状,并给出证明.思考:还有其他证明方法吗?向量的数量积是否为零,是判断相应的两条线段或直线是否垂直的重要方法之一练习已知a=(λ,2),b=(-3,5),且a和b的夹角是钝角,则λ的范围是[ ]BA练习B练习分析:为求a与b夹角,需先求a·b及|a||b|,再结合夹角θ的范围确定其值. 0≤θ≤π解记a与b的夹角为θ又0≤θ≤π知三角形函数值求角时,应注重角的范围的确定 已知a=(3,4),b=(4,3),求x,y的值使(xa+yb)⊥a,且|xa+yb|=1. 练习小结A、B两点间的距离公式:已知小结2.向量的坐标运算沟通了向量与解析几何的内在联系,解析几何中与角度、距离、平行、垂直有关的问题,可以考虑用向量方法来解决. 作业课本第121页习题2.4A组题6,7,8Thank you!
