2015年秋高中数学北师大版必修五课件:1.1正弦定理(共18张PPT)
文档属性
| 名称 | 2015年秋高中数学北师大版必修五课件:1.1正弦定理(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 602.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 00:00:00 | ||
图片预览






文档简介
课件18张PPT。第二章 解三角形1.1 正弦定理问题提出1、角的关系
2、边的关系
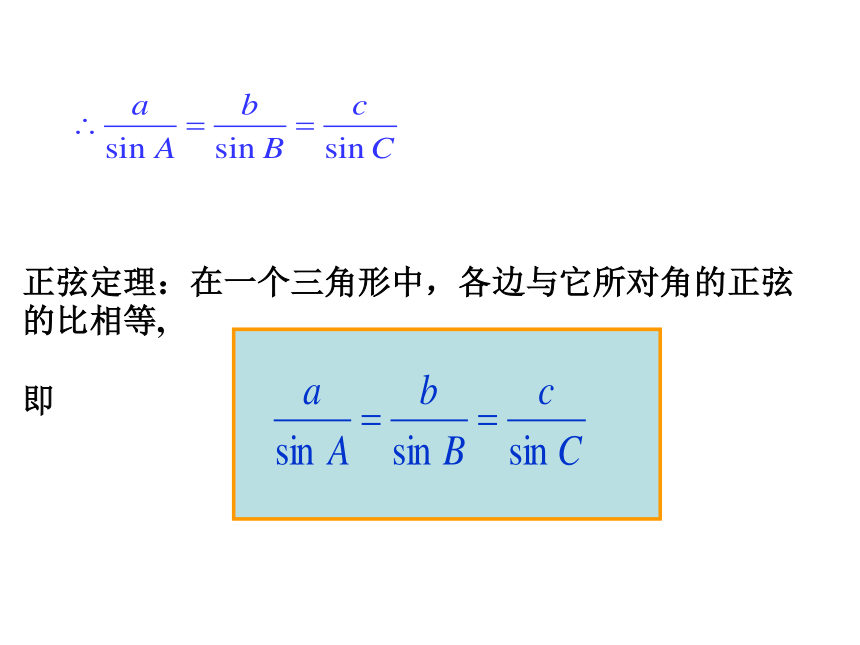
3、边角关系大角对大边三角形的边与角之间有什么关系?问题提出∴sinA=那么对于非直角三角形,这一关系式是否成立呢?,sinB= , sinC=1= .分析理解如图,以A为原点,以射线AB的方向为x轴正方向建立直角坐标系,C点在y轴上的射影为C’.正弦定理:在一个三角形中,各边与它所对角的正弦的比相等,
即 利用正弦定理,可以解决以下两类有关三角形的问题:
(1)已知两角和任一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边和两角。例1:某地出土一块类似三角形刀状的古代玉佩,其一角已破损.现测得如下数据:BC=2.57cm,CE=3.57cm,BD=4.38cm, B=45O, C=120O.为了复原,请计算原玉佩两边的长(结果精确到0.01cm)?
分析 如图,将BD,CE分别延长相交于一点A.在△ABC中已知BC的长及角B与C,可以通过正弦定理求AB,AC的长.解 将BD,CE分别延长相交于一点A.在△ABC中,BC=2.57cm, B=45O, C=120OA=180O-(B+C)=15O利用计算器算得同理,答 原玉佩两边的长分别约为7.02cm,3.15cm.例2:台风中心位于某市正东方向300km处,正以40km/h的速度向西北方向移动,距离台风中心250km范围内将会受其影响.如果台风风速不变,那么该市从何时起要遭受台风影响?这种影响持续多长时间(结果精确到0.1h)?
分析 如图,设该市在点A,台风中心从点B向西北方向移动,AB=300km.在台风中心移动过程中,当该中心到点A的距离不大于250km时,该市受台风影响.解 设台风中心从点B向西北方向沿射线BD移动,该市位于点B正西方向300km处的点A.假设经过t h,台风中心到达点C,则在△ABC中AB=300km,AC=250km,BC=40t km,B=45O,由正弦定理.知解得当同理,当答 约2时后将要遭受台风影响,持续约6.6时.已知两边一对角,三角形解的个数正弦定理的推论: 证明:如图,圆⊙O为△ABC的外接圆, BD为直径, 则 ∠A=∠D,例3:如图,在△ABC中, 求证: △ABC的面积 .证明练习( B )( D )练习(4)在任一 中,求证: 证明:由于正弦定理:令 ∴ 等式成立=右边小结(2)正弦定理的证明(3)正弦定理的应用(1)正弦定理的内容.
2、边的关系
3、边角关系大角对大边三角形的边与角之间有什么关系?问题提出∴sinA=那么对于非直角三角形,这一关系式是否成立呢?,sinB= , sinC=1= .分析理解如图,以A为原点,以射线AB的方向为x轴正方向建立直角坐标系,C点在y轴上的射影为C’.正弦定理:在一个三角形中,各边与它所对角的正弦的比相等,
即 利用正弦定理,可以解决以下两类有关三角形的问题:
(1)已知两角和任一边,求其他两边和一角;
(2)已知两边和其中一边的对角,求另一边和两角。例1:某地出土一块类似三角形刀状的古代玉佩,其一角已破损.现测得如下数据:BC=2.57cm,CE=3.57cm,BD=4.38cm, B=45O, C=120O.为了复原,请计算原玉佩两边的长(结果精确到0.01cm)?
分析 如图,将BD,CE分别延长相交于一点A.在△ABC中已知BC的长及角B与C,可以通过正弦定理求AB,AC的长.解 将BD,CE分别延长相交于一点A.在△ABC中,BC=2.57cm, B=45O, C=120OA=180O-(B+C)=15O利用计算器算得同理,答 原玉佩两边的长分别约为7.02cm,3.15cm.例2:台风中心位于某市正东方向300km处,正以40km/h的速度向西北方向移动,距离台风中心250km范围内将会受其影响.如果台风风速不变,那么该市从何时起要遭受台风影响?这种影响持续多长时间(结果精确到0.1h)?
分析 如图,设该市在点A,台风中心从点B向西北方向移动,AB=300km.在台风中心移动过程中,当该中心到点A的距离不大于250km时,该市受台风影响.解 设台风中心从点B向西北方向沿射线BD移动,该市位于点B正西方向300km处的点A.假设经过t h,台风中心到达点C,则在△ABC中AB=300km,AC=250km,BC=40t km,B=45O,由正弦定理.知解得当同理,当答 约2时后将要遭受台风影响,持续约6.6时.已知两边一对角,三角形解的个数正弦定理的推论: 证明:如图,圆⊙O为△ABC的外接圆, BD为直径, 则 ∠A=∠D,例3:如图,在△ABC中, 求证: △ABC的面积 .证明练习( B )( D )练习(4)在任一 中,求证: 证明:由于正弦定理:令 ∴ 等式成立=右边小结(2)正弦定理的证明(3)正弦定理的应用(1)正弦定理的内容.
