2015年秋高中数学北师大版必修五课件:1.1不等关系(共16张PPT)
文档属性
| 名称 | 2015年秋高中数学北师大版必修五课件:1.1不等关系(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 640.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 00:00:00 | ||
图片预览






文档简介
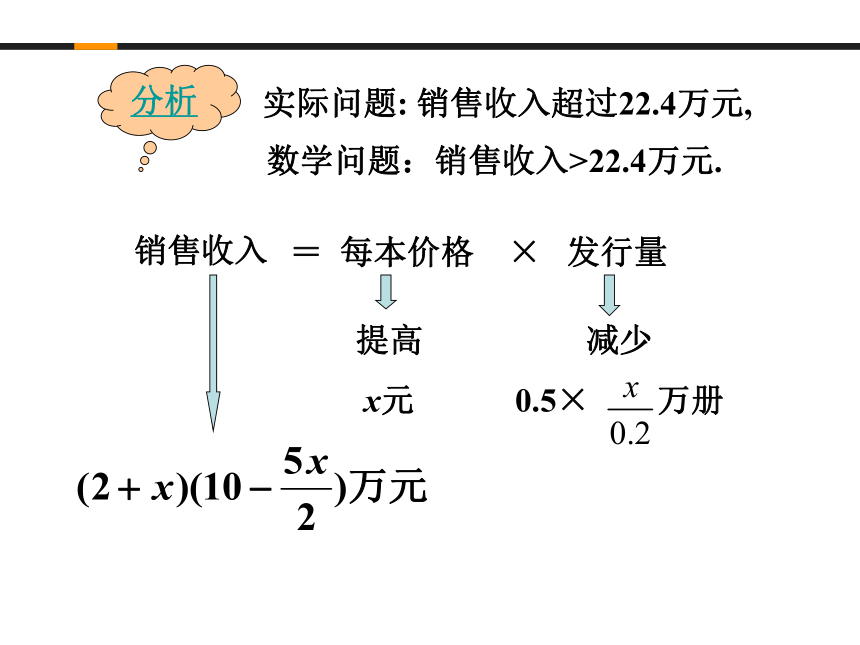
课件16张PPT。第三章 不等式1.1 不等关系实际生活中:长 短大 小轻 重高 矮一、问题情境 1.这是某酸奶的质量检查规定 用数学关系来反映就是二、学生活动从表格中你能获得什么信息?二、学生活动 例1.某杂志以每本2元的价格发行时,发行量为10万册. 经过调查,若价格每提高0.2元,发行量就减少5000册. 若设每本杂志的定价提高x元,怎样才能使杂志社的销售收入超过22.4万元?(不求解).解:设每本杂志价格提高x元,由题意,得 化简,得(这是一元二次不等式问题)三、数学应用分析实际问题: 销售收入超过22.4万元,销售收入= 每本价格 × 发行量提高
x元减少
0.5× 万册数学问题:销售收入>22.4万元. 变式.某杂志以每本2元的价格发行时,发行量为10万册. 经过调查,若价格每提高0.2元,发行量就减少5000册. 为获得最大利润,该杂志的最佳售价为多少元?解:设每本杂志价格提高x元,总利润为y元.
由题意,得 化简,得(这是二次函数问题)三、数学应用例2.下表给出了甲,乙,丙三种食物的维生素含量及成本:某人将这三种食物混合成100kg的食品,要使混合食品中至少含35000单位的维生素A及40000单位的维生素B,设甲,乙这两种食物各取x kg,y kg,那么x,y应满足怎样的关系?(不求解)解:由题意,得 即:(这是一个不等式组)x≥0
y≥0三、数学应用x≥0
2x-y ≥50
y≥25100kg食品大于等于 35000 大于等于40000分析例3.
从这张图上你可以得到什么样的不等关系?(不求解)三、数学应用解:由图可得0(体现了不等式和图象的联系)分析抛物线在直线上方1.某种植物适宜生长的温度为18℃--20℃的山区,已知山区海拔每升高100m,气温下降0.55℃.现测得山脚下的平均气温为22℃,该植物种在山区多高处为宜?
四、反馈练习(不求解) 解:设该植物适宜的种植高度为xm,由题意,得18≤22 - ≤20. 解:设明年的产量为x袋,则 4x≤200×2100x≥800000.02x≤600+12002.某化工厂制定明年某产品的生产计划,受下面条件的制约:生产此产品的工人数不超过200人;每个工人年工作约计2100h;预计此产品明年销售量至少80000袋;每袋需用4h;每袋需要原料20kg;年底库存原料600t,明年可补充1200t.试根据这些数据预测明年的产量.四、反馈练习3.用今天所学的数学知识来解释生活中“糖水加糖甜更甜”的现象.四、反馈练习即b克糖水中有a克糖(b>a>0),若再添加m克糖(m>0),则糖水更甜了.试根据这一事实,提炼出一个不等式.4.经长期观察某港口水的深度y是时间t(0≤t≤24)的函数且近似满足关系式y=3sin t+10. 一般情况下船舶航行时船底离海底的距离为5m或5m以上认为安全. 某船的吃水深度6.5m. 在同一天内,问该船何时能安全进出港口?(不求解)
解:由题意,得 四、反馈练习五、回顾反思1.解决实际问题的常规步骤实际问题 抽象、概括数学问题;刻画2.本堂课建立的模型主要是不等关系.
x元减少
0.5× 万册数学问题:销售收入>22.4万元. 变式.某杂志以每本2元的价格发行时,发行量为10万册. 经过调查,若价格每提高0.2元,发行量就减少5000册. 为获得最大利润,该杂志的最佳售价为多少元?解:设每本杂志价格提高x元,总利润为y元.
由题意,得 化简,得(这是二次函数问题)三、数学应用例2.下表给出了甲,乙,丙三种食物的维生素含量及成本:某人将这三种食物混合成100kg的食品,要使混合食品中至少含35000单位的维生素A及40000单位的维生素B,设甲,乙这两种食物各取x kg,y kg,那么x,y应满足怎样的关系?(不求解)解:由题意,得 即:(这是一个不等式组)x≥0
y≥0三、数学应用x≥0
2x-y ≥50
y≥25100kg食品大于等于 35000 大于等于40000分析例3.
从这张图上你可以得到什么样的不等关系?(不求解)三、数学应用解:由图可得0(体现了不等式和图象的联系)分析抛物线在直线上方1.某种植物适宜生长的温度为18℃--20℃的山区,已知山区海拔每升高100m,气温下降0.55℃.现测得山脚下的平均气温为22℃,该植物种在山区多高处为宜?
四、反馈练习(不求解) 解:设该植物适宜的种植高度为xm,由题意,得18≤22 - ≤20. 解:设明年的产量为x袋,则 4x≤200×2100x≥800000.02x≤600+12002.某化工厂制定明年某产品的生产计划,受下面条件的制约:生产此产品的工人数不超过200人;每个工人年工作约计2100h;预计此产品明年销售量至少80000袋;每袋需用4h;每袋需要原料20kg;年底库存原料600t,明年可补充1200t.试根据这些数据预测明年的产量.四、反馈练习3.用今天所学的数学知识来解释生活中“糖水加糖甜更甜”的现象.四、反馈练习即b克糖水中有a克糖(b>a>0),若再添加m克糖(m>0),则糖水更甜了.试根据这一事实,提炼出一个不等式.4.经长期观察某港口水的深度y是时间t(0≤t≤24)的函数且近似满足关系式y=3sin t+10. 一般情况下船舶航行时船底离海底的距离为5m或5m以上认为安全. 某船的吃水深度6.5m. 在同一天内,问该船何时能安全进出港口?(不求解)
解:由题意,得 四、反馈练习五、回顾反思1.解决实际问题的常规步骤实际问题 抽象、概括数学问题;刻画2.本堂课建立的模型主要是不等关系.
