2015年秋高中数学北师大版必修五课件:3.1基本不等式(共13张PPT)
文档属性
| 名称 | 2015年秋高中数学北师大版必修五课件:3.1基本不等式(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 830.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
第三章 不等式
3.1 基本不等式
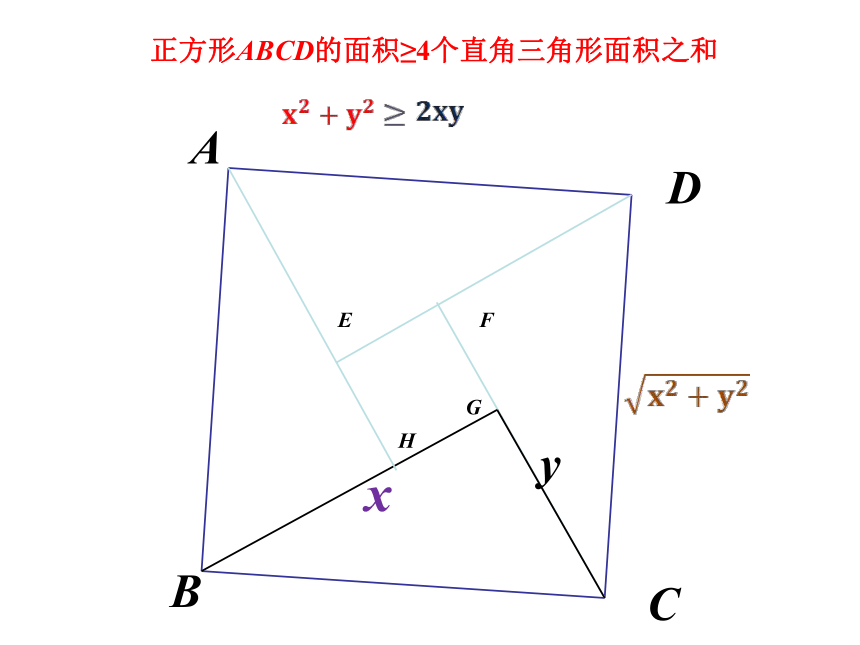
国际数学大会(ICM2002)的会标
x
y
A
B
C
D
正方形ABCD的面积≥4个直角三角形面积之和
E
F
G
H
如果令x= , y= , 则就称为
如果a,b都是非负数,那么 ,
当且仅当a=b时,等号成立。
我们把 称为基本不等式
基本不等式
(均值不等式)
称为a,b的算术平均数
称为a,b的几何平均数
A
C
B
D
O
令AC= a , CB= b
因为
所以
当且仅当C与O重合,即a=b时,等号成立
例1、设a,b均为正数,
证明 不等式
证明 因为a,b均为正数,由基本不等式,可知
也即
当且仅当a=b时,等号成立
下面给出这个不等式的几何解释.
E
对基本不等式,用语言文字可叙述为:
两个正数的算术平均数不小于它们的几何平均数。
从几何的角度可叙述为:
圆的半径不小于弦长的一半。
从数列的角度可叙述为:
两个正数的等差中项不小于它们的等比中项。
课堂作业:
想一想?
由基本不等式,例1和练习题你能给出这几式子的大小关系吗?
小结:
1.两个重要的不等式
2.基本不等式的联系和体会
3.对基本不等式和例1及练习题的总结
当且仅当a=b时,等号成立
第三章 不等式
3.1 基本不等式
国际数学大会(ICM2002)的会标
x
y
A
B
C
D
正方形ABCD的面积≥4个直角三角形面积之和
E
F
G
H
如果令x= , y= , 则就称为
如果a,b都是非负数,那么 ,
当且仅当a=b时,等号成立。
我们把 称为基本不等式
基本不等式
(均值不等式)
称为a,b的算术平均数
称为a,b的几何平均数
A
C
B
D
O
令AC= a , CB= b
因为
所以
当且仅当C与O重合,即a=b时,等号成立
例1、设a,b均为正数,
证明 不等式
证明 因为a,b均为正数,由基本不等式,可知
也即
当且仅当a=b时,等号成立
下面给出这个不等式的几何解释.
E
对基本不等式,用语言文字可叙述为:
两个正数的算术平均数不小于它们的几何平均数。
从几何的角度可叙述为:
圆的半径不小于弦长的一半。
从数列的角度可叙述为:
两个正数的等差中项不小于它们的等比中项。
课堂作业:
想一想?
由基本不等式,例1和练习题你能给出这几式子的大小关系吗?
小结:
1.两个重要的不等式
2.基本不等式的联系和体会
3.对基本不等式和例1及练习题的总结
当且仅当a=b时,等号成立
