2015年秋高中数学北师大版必修五课件:1.2数列的函数特性(共25张PPT)
文档属性
| 名称 | 2015年秋高中数学北师大版必修五课件:1.2数列的函数特性(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 14:05:42 | ||
图片预览








文档简介
课件25张PPT。 1.2 数列的函数特性第一章 数 列 数列可以看作是一个定义域为N*(正整数集)或它的有限子集{1,2,3,…,k}的函数(“离散型”函数),当自变量由小到大的顺序依次取值时所对应的一列函数值。数列的通项公式an=f(n)是数列的第n项an与自变量n之间的函数解析式,数列的图象是横坐标为正整数的一系列的离散的点。
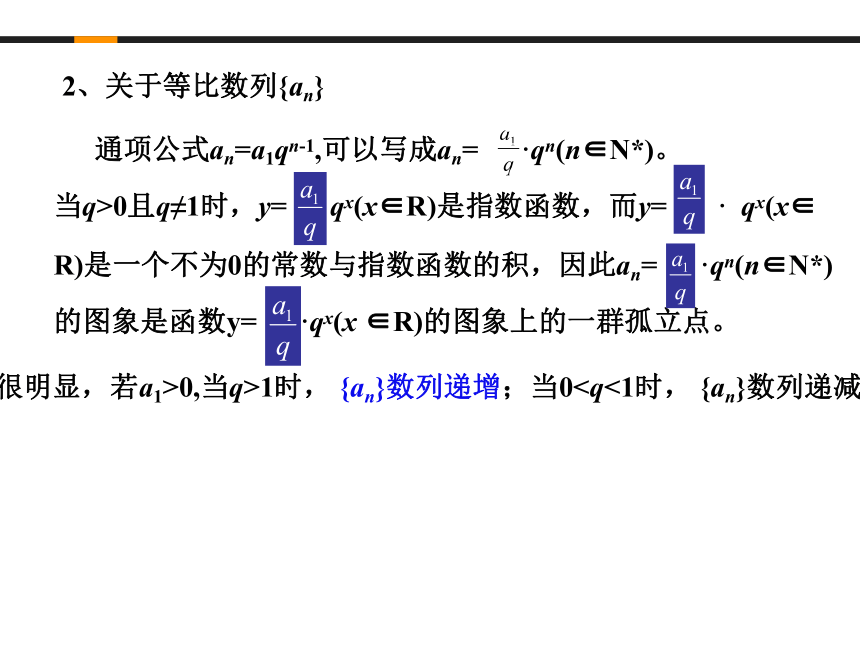
数列作为一种特殊的函数,具有函数的本质属性,我们称之为数列的函数特性,即用函数的观点来理解数列,解决数列中的某些问题。事实上,任何数列问题都蕴含着函数的本质及意义,具有函数的一些固有特征。作为特殊的函数,数列是函数概念的继续和延伸。另外,数列与函数的整合也是当今高考命题的重点与热点,因此我们在解决数列问题时,应充分利用函数有关知识,以它的概念、图象、性质为纽带,架起函数与数列间的桥梁,揭示它们间的内在联系,从而有效地学好数列问题。因此,学完《数列》后,一方面要用函数的观点加深了解数列,拓展我们的知识,提升我们的能力;另一方面也为今后学习高等数学中有关级数的知识和解决现实生活中的一些实际问题打下了基础。一、以函数观点为切入点 深刻认识数列问题 1、关于等差数列{an}(1)通项公式an=a1+(n-1)d,可以写成an=dn+(a1-d)。它是n的一次函数,以(n,an)为坐标的一群离散点均匀地分布在直线上。当d>0时, {an}数列递增;当d<0时, {an}数列递减;当d=0时,{an}为常数数列。 (2)求和公式Sn=na1+d,可以写成Sn= n2+(a1-)n,它是n的二次函数(缺常数项),它的图象是过原点的抛物线上的一群孤立点。 2、关于等比数列{an}很明显,若a1>0,当q>1时, {an}数列递增;当00,使结论成立②当时 ,若条件①成立,因此时,但 时,不满足条件②,即不存在常数c>0,使结论成立.综合①②,即不存在常数c>0,使结论成立.六、把握数列的函数特性 辨析函数与数列联系与区别?(2)已知{an}是递增数列,且对任意n∈N*都有an=n2+λn恒成立,则实数λ的取值范围是( )
A. ( ,+∞) B.(0,+∞)?
C.(-2,+∞) D.(-3,+∞) 例7:(1)已知函数 在区间[1, +∞)是增函数,则实数λ的取值范围是( )
A. ( ,+∞) B.(0,+∞)
? C.(-2,+∞) D.(-3,+∞)练习:若数列{an}的通项公式为an=-n2+7n(n∈N*),求an的最大值,并与函数y=-x2+7x(x∈R)的最大值作比较 解: 作出函数y=-x2+7x(x∈R)的 图象.
从图象上看,表示数列{an}的各点都在抛物线y=-x2+7x(x∈R)上,由图象得 说明 经比较发现数列{an}与函数y=-x2+7x(x∈R)在不同的地方取到不同的最大值,这是由于两者的定义域不同所造成的.
数列作为一种特殊的函数,具有函数的本质属性,我们称之为数列的函数特性,即用函数的观点来理解数列,解决数列中的某些问题。事实上,任何数列问题都蕴含着函数的本质及意义,具有函数的一些固有特征。作为特殊的函数,数列是函数概念的继续和延伸。另外,数列与函数的整合也是当今高考命题的重点与热点,因此我们在解决数列问题时,应充分利用函数有关知识,以它的概念、图象、性质为纽带,架起函数与数列间的桥梁,揭示它们间的内在联系,从而有效地学好数列问题。因此,学完《数列》后,一方面要用函数的观点加深了解数列,拓展我们的知识,提升我们的能力;另一方面也为今后学习高等数学中有关级数的知识和解决现实生活中的一些实际问题打下了基础。一、以函数观点为切入点 深刻认识数列问题 1、关于等差数列{an}(1)通项公式an=a1+(n-1)d,可以写成an=dn+(a1-d)。它是n的一次函数,以(n,an)为坐标的一群离散点均匀地分布在直线上。当d>0时, {an}数列递增;当d<0时, {an}数列递减;当d=0时,{an}为常数数列。 (2)求和公式Sn=na1+d,可以写成Sn= n2+(a1-)n,它是n的二次函数(缺常数项),它的图象是过原点的抛物线上的一群孤立点。 2、关于等比数列{an}很明显,若a1>0,当q>1时, {an}数列递增;当0
A. ( ,+∞) B.(0,+∞)?
C.(-2,+∞) D.(-3,+∞) 例7:(1)已知函数 在区间[1, +∞)是增函数,则实数λ的取值范围是( )
A. ( ,+∞) B.(0,+∞)
? C.(-2,+∞) D.(-3,+∞)练习:若数列{an}的通项公式为an=-n2+7n(n∈N*),求an的最大值,并与函数y=-x2+7x(x∈R)的最大值作比较 解: 作出函数y=-x2+7x(x∈R)的 图象.
从图象上看,表示数列{an}的各点都在抛物线y=-x2+7x(x∈R)上,由图象得 说明 经比较发现数列{an}与函数y=-x2+7x(x∈R)在不同的地方取到不同的最大值,这是由于两者的定义域不同所造成的.
