苏教版小学数学五年级下册3.10 《和与积的奇偶性》课件(共17张PPT)
文档属性
| 名称 | 苏教版小学数学五年级下册3.10 《和与积的奇偶性》课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 694.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 13:08:16 | ||
图片预览





文档简介
(共17张PPT)
3.10 和与积的奇偶性
苏教版小学数学五年级下册
1、使学生经历探索和与积的奇偶性的规律的过程,发现并理解和与积的奇偶性的规律,能判断加法和乘法的得数是奇数还是偶数,并能说明理由。
2、使学生通过举例观察、比较、猜想、验证、发现和以及奇偶性的规律,建立探索规律的经验。
3、使学生主动参与探索规律的活动,体会数学内容具有规律性,产生对数学学习的兴趣。
学习重点:探究并发现和与积奇偶性规律。
学习难点:理解归纳规律。
学习目标
一、情境引入、激发思考:
如果不计算,你能直接判断
1+3+5+…+29的和是奇数还是偶数吗?
你是怎么想的?
二、主动探究、发现规律:
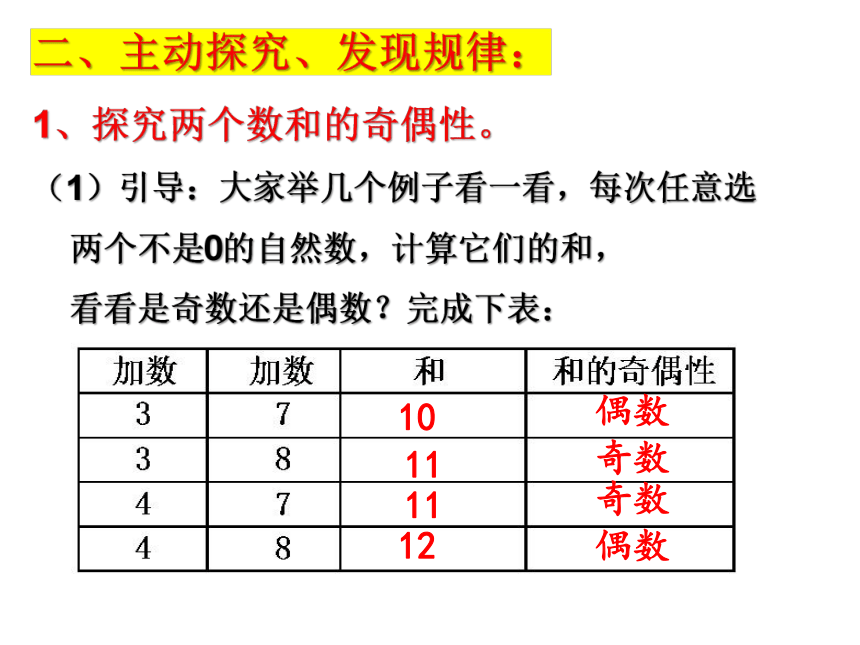
1、探究两个数和的奇偶性。
(1)引导:大家举几个例子看一看,每次任意选
两个不是0的自然数,计算它们的和,
看看是奇数还是偶数?完成下表:
10
偶数
11
奇数
11
奇数
12
偶数
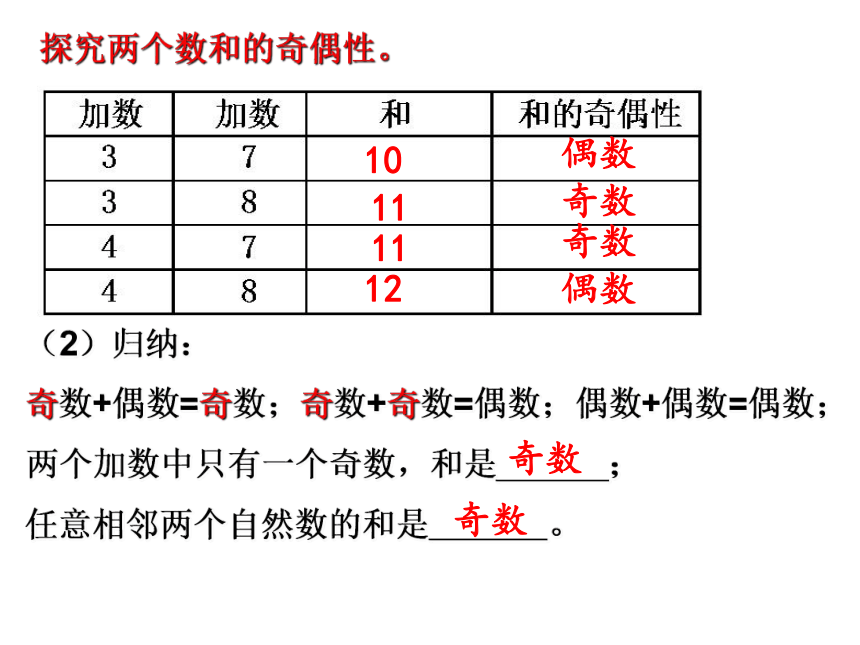
探究两个数和的奇偶性。
10
偶数
11
奇数
11
奇数
12
偶数
(2)归纳:
奇数+偶数=奇数;奇数+奇数=偶数;偶数+偶数=偶数;
两个加数中只有一个奇数,和是 ;
任意相邻两个自然数的和是 。
奇数
奇数
2、探究几个数连加和的奇偶性。
(1)分析;因为任意个偶数的和一定是偶数,
所以几个加数的和与奇数的个数有重要关系。
(2)算一算:
1+3= ;1+3+5= ;1+3+5+7= ;
1+3+5+7+9= ;1+3+5+7+9+11= ;
(3)归纳:
加数里奇数个数是奇数时,和为奇数;
加数里奇数个数是偶数时,和为偶数;简记为:奇奇得奇,奇偶得偶。
4
9
16
25
36
4、回顾反思,积累经验:
一是遇到复杂问题,可以从简单的问题入手,找出规律来解决;
二是探索规律时,先举出一类例子,再观察、比较,
寻找有什么特点,从中发现规律。
3、应用规律,判断结果:
再看1+3+5+…+29的和是奇数还是偶数?
因为1--29奇数里共有 个奇数,
所以它的和为 。
15
奇数
5、探究积的奇偶性。
引导:81×3×675×7×8×11×814×19×15×121
积是奇数还是偶数吗?
几个数的乘积,什么情况下是奇数?什么情况下是偶数?
观察:1×3×5=15; 8×4×10×2=640;
1×2×3=6; 3×5×7×2=210。
应用规律判断:81×3×675×7×8×11×814×19×15×121积是 数。
归纳:
乘数都是奇数,积也是奇数;乘数都是偶数,积也是偶数。
几个乘数中,只要有一个偶数,积一定是偶数。
偶
试一试:
(1)1+2+3+4+……+99+100的和是奇数还是偶数?
(2)1×2×3×4×……×99的积是奇数还是偶数?
三、例题讲解:
例1、有一行数1、1、2、3、5、8、13、21、34、55、…从第三个数开始,每个数都是前两个数的和,
在前100个数中,偶数有多少个?
例2、
(1)1+2+3+…+1000+1001的和是奇数还是偶数?
(2)1×2×3×…×1000×1001的积是奇数还是偶数?
三、基础强化:
1、判断对错:(对的打“√”,错的打“×”)
(1)两个奇数的积,再加上一个偶数,和是( )
A、奇数 B、偶数 C、奇数或偶数
(2)一个奇数如果( ),结果是偶数。
A、乘5 B、加上1 C、除以3 D、减去2
(3)两个奇数的积,再加上偶数,结果一定是( )
A、奇数 B、偶数 C、奇数或偶数
(4)a是一个奇数,以下算式:(1)a+4;(2)6a;
(3)a+3;(4)a2;(5)a+a。
其中结果是偶数的算式有( )
A、2个 B、3个 C、4个 D、5个
2、不计算,直接判断下面算式结果
是奇数还是偶数。
(1)34×92×86 ( )
(2)47×35×61×253 ( )
(3)17+12+25+19+37+10 ( )
(4)39+24+18+57+42 ( )
4、50个橘子放到17个盘子,每个盘子里
只能放奇数个,能否做到,为什么?
3、按要求在 里填上合适的数字。
(1)结果是奇数:11235+908
(2)结果是偶数 458-23
(3)结果是奇数 783 ×61
(4)结果是偶数 29 ×89
四、拓展提高:
在下面的数中添3个“+”,改写成四个数
相加的和是奇数的等式(试写出三种情况)
1 2 3 4 5 6 7 8 9 10=奇数
1 2 3 4 5 6 7 8 9 10=奇数
1 2 3 4 5 6 7 8 9 10=奇数
五、总结反思:1、两个加数中只有一个奇数,和是奇数;
任意相邻两个自然数的和是奇数。
2、几个数连加和的奇偶性:
奇奇得奇,奇偶得偶。
3、积的奇偶性:
几个乘数中,只要有一个偶数,积一定是偶数。
六、随堂检测:
1、奇数+奇数 =( ) 偶数+偶数 =( )
奇数×奇数=( ) 偶数×偶数=( )
2、第一次按开关灯亮,第二次按开关灯灭,
依次这样按下去,第12次按开关灯( ),
第23次按开关灯( )。
3、4个连续自然数的和是奇数还是偶数?举例说明。
3.10 和与积的奇偶性
苏教版小学数学五年级下册
1、使学生经历探索和与积的奇偶性的规律的过程,发现并理解和与积的奇偶性的规律,能判断加法和乘法的得数是奇数还是偶数,并能说明理由。
2、使学生通过举例观察、比较、猜想、验证、发现和以及奇偶性的规律,建立探索规律的经验。
3、使学生主动参与探索规律的活动,体会数学内容具有规律性,产生对数学学习的兴趣。
学习重点:探究并发现和与积奇偶性规律。
学习难点:理解归纳规律。
学习目标
一、情境引入、激发思考:
如果不计算,你能直接判断
1+3+5+…+29的和是奇数还是偶数吗?
你是怎么想的?
二、主动探究、发现规律:
1、探究两个数和的奇偶性。
(1)引导:大家举几个例子看一看,每次任意选
两个不是0的自然数,计算它们的和,
看看是奇数还是偶数?完成下表:
10
偶数
11
奇数
11
奇数
12
偶数
探究两个数和的奇偶性。
10
偶数
11
奇数
11
奇数
12
偶数
(2)归纳:
奇数+偶数=奇数;奇数+奇数=偶数;偶数+偶数=偶数;
两个加数中只有一个奇数,和是 ;
任意相邻两个自然数的和是 。
奇数
奇数
2、探究几个数连加和的奇偶性。
(1)分析;因为任意个偶数的和一定是偶数,
所以几个加数的和与奇数的个数有重要关系。
(2)算一算:
1+3= ;1+3+5= ;1+3+5+7= ;
1+3+5+7+9= ;1+3+5+7+9+11= ;
(3)归纳:
加数里奇数个数是奇数时,和为奇数;
加数里奇数个数是偶数时,和为偶数;简记为:奇奇得奇,奇偶得偶。
4
9
16
25
36
4、回顾反思,积累经验:
一是遇到复杂问题,可以从简单的问题入手,找出规律来解决;
二是探索规律时,先举出一类例子,再观察、比较,
寻找有什么特点,从中发现规律。
3、应用规律,判断结果:
再看1+3+5+…+29的和是奇数还是偶数?
因为1--29奇数里共有 个奇数,
所以它的和为 。
15
奇数
5、探究积的奇偶性。
引导:81×3×675×7×8×11×814×19×15×121
积是奇数还是偶数吗?
几个数的乘积,什么情况下是奇数?什么情况下是偶数?
观察:1×3×5=15; 8×4×10×2=640;
1×2×3=6; 3×5×7×2=210。
应用规律判断:81×3×675×7×8×11×814×19×15×121积是 数。
归纳:
乘数都是奇数,积也是奇数;乘数都是偶数,积也是偶数。
几个乘数中,只要有一个偶数,积一定是偶数。
偶
试一试:
(1)1+2+3+4+……+99+100的和是奇数还是偶数?
(2)1×2×3×4×……×99的积是奇数还是偶数?
三、例题讲解:
例1、有一行数1、1、2、3、5、8、13、21、34、55、…从第三个数开始,每个数都是前两个数的和,
在前100个数中,偶数有多少个?
例2、
(1)1+2+3+…+1000+1001的和是奇数还是偶数?
(2)1×2×3×…×1000×1001的积是奇数还是偶数?
三、基础强化:
1、判断对错:(对的打“√”,错的打“×”)
(1)两个奇数的积,再加上一个偶数,和是( )
A、奇数 B、偶数 C、奇数或偶数
(2)一个奇数如果( ),结果是偶数。
A、乘5 B、加上1 C、除以3 D、减去2
(3)两个奇数的积,再加上偶数,结果一定是( )
A、奇数 B、偶数 C、奇数或偶数
(4)a是一个奇数,以下算式:(1)a+4;(2)6a;
(3)a+3;(4)a2;(5)a+a。
其中结果是偶数的算式有( )
A、2个 B、3个 C、4个 D、5个
2、不计算,直接判断下面算式结果
是奇数还是偶数。
(1)34×92×86 ( )
(2)47×35×61×253 ( )
(3)17+12+25+19+37+10 ( )
(4)39+24+18+57+42 ( )
4、50个橘子放到17个盘子,每个盘子里
只能放奇数个,能否做到,为什么?
3、按要求在 里填上合适的数字。
(1)结果是奇数:11235+908
(2)结果是偶数 458-23
(3)结果是奇数 783 ×61
(4)结果是偶数 29 ×89
四、拓展提高:
在下面的数中添3个“+”,改写成四个数
相加的和是奇数的等式(试写出三种情况)
1 2 3 4 5 6 7 8 9 10=奇数
1 2 3 4 5 6 7 8 9 10=奇数
1 2 3 4 5 6 7 8 9 10=奇数
五、总结反思:1、两个加数中只有一个奇数,和是奇数;
任意相邻两个自然数的和是奇数。
2、几个数连加和的奇偶性:
奇奇得奇,奇偶得偶。
3、积的奇偶性:
几个乘数中,只要有一个偶数,积一定是偶数。
六、随堂检测:
1、奇数+奇数 =( ) 偶数+偶数 =( )
奇数×奇数=( ) 偶数×偶数=( )
2、第一次按开关灯亮,第二次按开关灯灭,
依次这样按下去,第12次按开关灯( ),
第23次按开关灯( )。
3、4个连续自然数的和是奇数还是偶数?举例说明。
