2015年秋高中数学北师大版必修五课件:3解三角形的实际应用举例(共11张PPT)
文档属性
| 名称 | 2015年秋高中数学北师大版必修五课件:3解三角形的实际应用举例(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 885.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 00:00:00 | ||
图片预览


文档简介
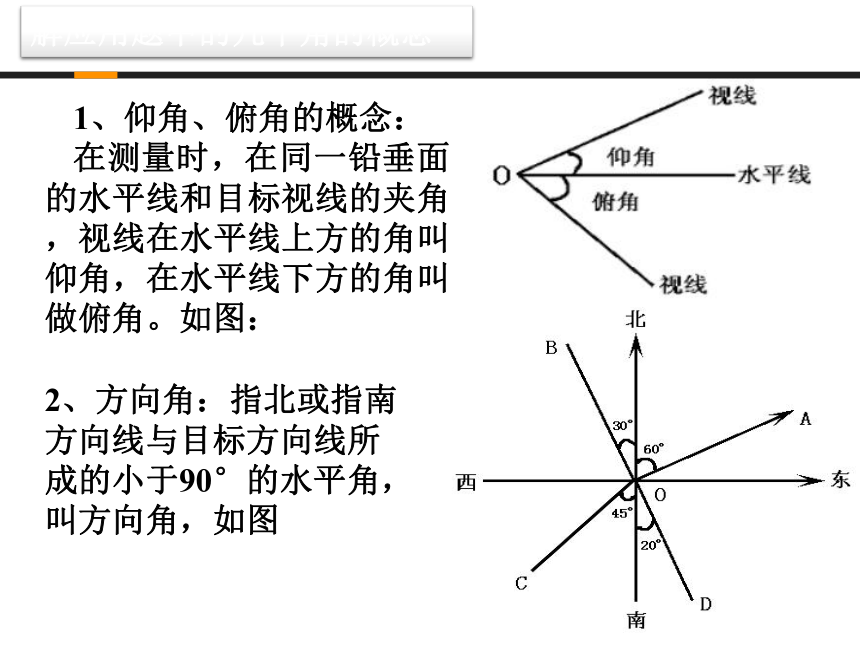
课件11张PPT。第二章 解三角形3 解三角形的实际应用举例1、正弦定理2、余弦定理解应用题中的几个角的概念1、仰角、俯角的概念:
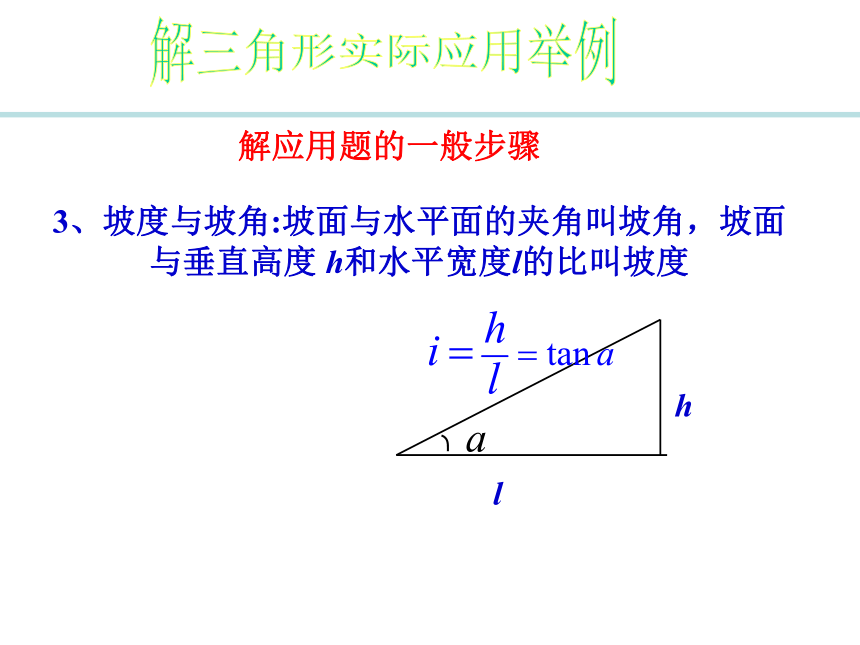
在测量时,在同一铅垂面的水平线和目标视线的夹角,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如图 解三角形实际应用举例解应用题的一般步骤3、坡度与坡角:坡面与水平面的夹角叫坡角,坡面与垂直高度 h和水平宽度l的比叫坡度hl(3)如图,在200 m 高的山顶A处,测得山下一塔顶C与塔底D的俯角分别是30?,60?,则塔高是 米。
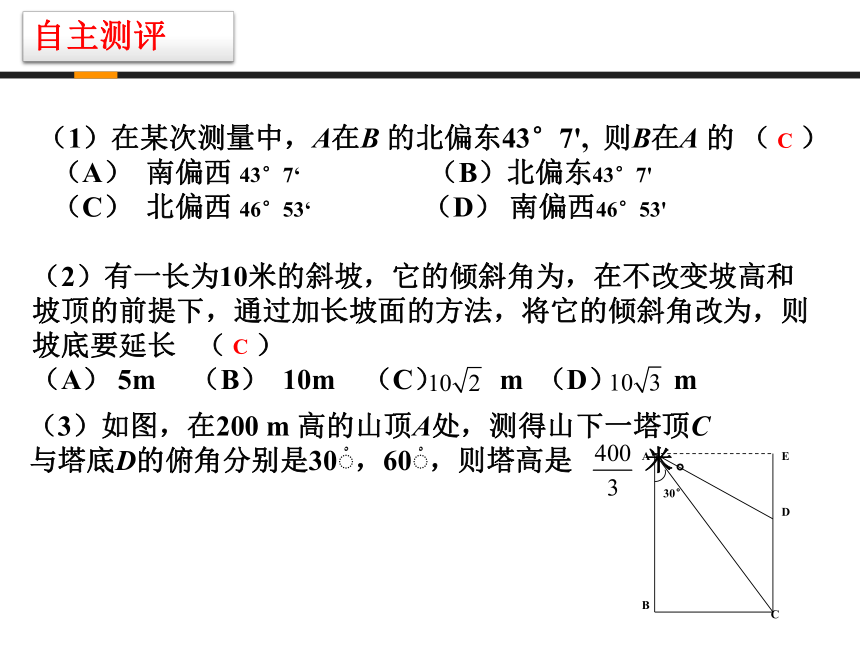
自主测评(1)在某次测量中,A在B 的北偏东43°7', 则B在A 的 ( )
(A) 南偏西 43°7‘ (B)北偏东43°7'
(C) 北偏西 46°53‘ (D) 南偏西46°53'C(2)有一长为10米的斜坡,它的倾斜角为,在不改变坡高和坡顶的前提下,通过加长坡面的方法,将它的倾斜角改为,则坡底要延长 ( )
(A) 5m (B) 10m (C) m (D) mC 解三角形实际应用举例 例1.如图,自动卸货汽车采用液压机构,设计时需要计算
油泵顶杆BC的长度(如图).已知车厢的最大仰角为60°,油
泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长度(结果精确到0.01m). (1)什么是最大仰角? (2)例题中涉及一个怎样的三角
形?在△ABC中已知什么,要求什么?例题讲解:测量距离与边长实例讲解解:由余弦定理,得答:顶杠BC长约为1.89m.1.40m1.95m例2、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在
同一水平直线上的C、D两处,测得烟囱的仰角分别是,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。
(精确到0.01米)图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想例题讲解:测量高度实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.89m.(1)解决实际应用问题的关键思想方法是把实际问题转化为数学问题,即数学建模思想。(2)解决实际应用问题的步骤实际问题数学问题(画出图形)解三角形问题数学结论分析转化检验总结提升课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解
在测量时,在同一铅垂面的水平线和目标视线的夹角,视线在水平线上方的角叫仰角,在水平线下方的角叫做俯角。如图:2、方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫方向角,如图 解三角形实际应用举例解应用题的一般步骤3、坡度与坡角:坡面与水平面的夹角叫坡角,坡面与垂直高度 h和水平宽度l的比叫坡度hl(3)如图,在200 m 高的山顶A处,测得山下一塔顶C与塔底D的俯角分别是30?,60?,则塔高是 米。
自主测评(1)在某次测量中,A在B 的北偏东43°7', 则B在A 的 ( )
(A) 南偏西 43°7‘ (B)北偏东43°7'
(C) 北偏西 46°53‘ (D) 南偏西46°53'C(2)有一长为10米的斜坡,它的倾斜角为,在不改变坡高和坡顶的前提下,通过加长坡面的方法,将它的倾斜角改为,则坡底要延长 ( )
(A) 5m (B) 10m (C) m (D) mC 解三角形实际应用举例 例1.如图,自动卸货汽车采用液压机构,设计时需要计算
油泵顶杆BC的长度(如图).已知车厢的最大仰角为60°,油
泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的
夹角为 ,AC长为1.40m,计算BC的长度(结果精确到0.01m). (1)什么是最大仰角? (2)例题中涉及一个怎样的三角
形?在△ABC中已知什么,要求什么?例题讲解:测量距离与边长实例讲解解:由余弦定理,得答:顶杠BC长约为1.89m.1.40m1.95m例2、如图,要测底部不能到达的烟囱的高AB,从与烟囱底部在
同一水平直线上的C、D两处,测得烟囱的仰角分别是,CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。
(精确到0.01米)图中给出了怎样的一个
几何图形?已知什么,
求什么?想一想例题讲解:测量高度实例讲解分析:如图,因为AB=AA1+A1B,又
已知AA1=1.5m,所以只要求出A1B即可。解:答:烟囱的高为 29.89m.(1)解决实际应用问题的关键思想方法是把实际问题转化为数学问题,即数学建模思想。(2)解决实际应用问题的步骤实际问题数学问题(画出图形)解三角形问题数学结论分析转化检验总结提升课堂小结1、本节课通过举例说明了解斜三角形在实际中的一些应用。
掌握利用正弦定理及余弦定理解任意三角形的方法。2、在分析问题解决问题的过程中关键要分析题意,分清已知
与所求,根据题意画出示意图,并正确运用正弦定理和余
弦定理解题。3、在解实际问题的过程中,贯穿了数学建模的思想,其流程
图可表示为:实际问题数学模型实际问题的解数学模型的解
