数学人教A版(2019)必修第二册8.4.2空间点、直线、平面的位置关系 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.4.2空间点、直线、平面的位置关系 课件(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 799.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 13:44:42 | ||
图片预览

文档简介
(共18张PPT)
8.4 空间点、直线、平面之间的关系
8.4.2 空间点、直线、平面的位置关系
复习与引入
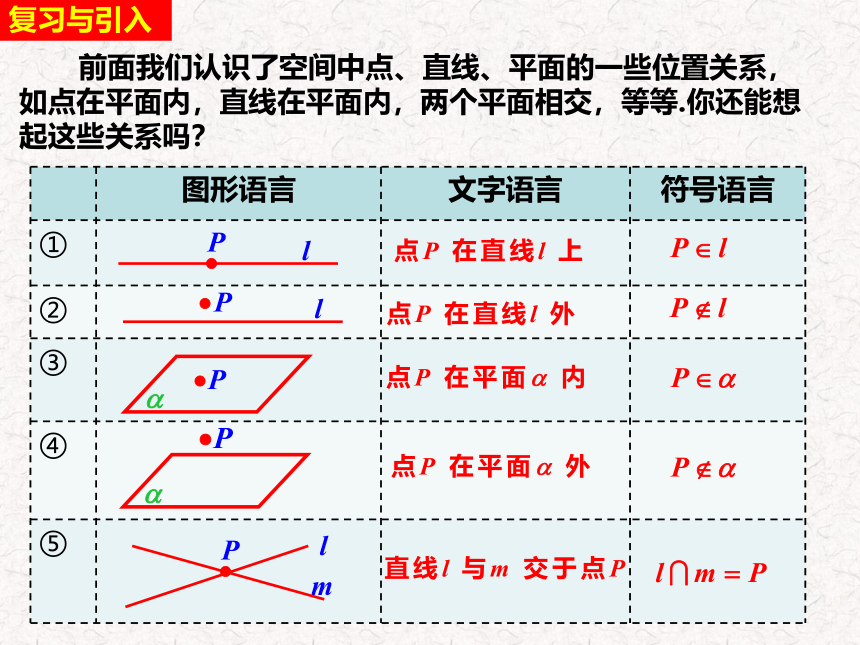
前面我们认识了空间中点、直线、平面的一些位置关系,如点在平面内,直线在平面内,两个平面相交,等等.你还能想起这些关系吗?
图形语言 文字语言 符号语言
①
②
③
④
⑤
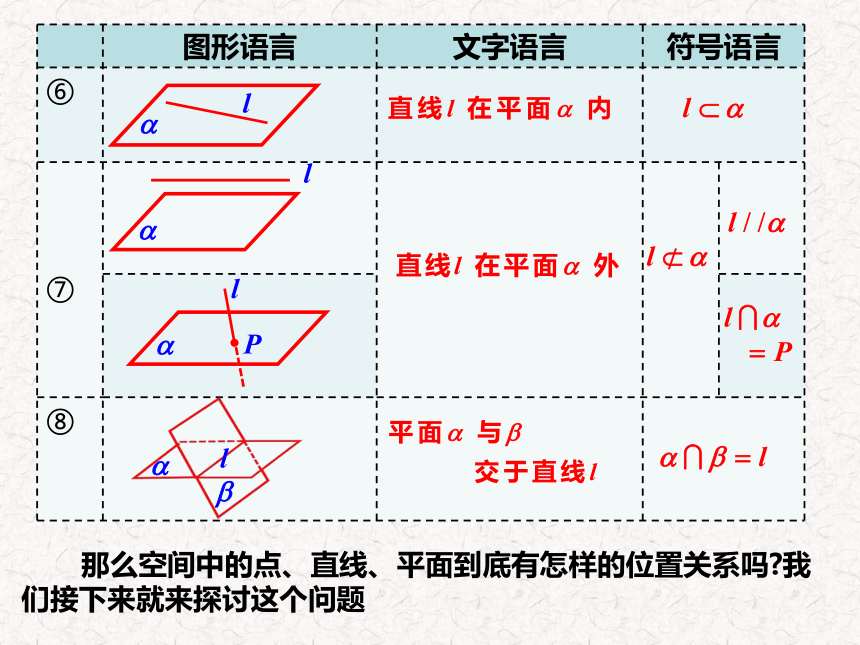
图形语言 文字语言 符号语言 ⑥ ⑦
⑧
那么空间中的点、直线、平面到底有怎样的位置关系吗 我们接下来就来探讨这个问题
知识探究(一)
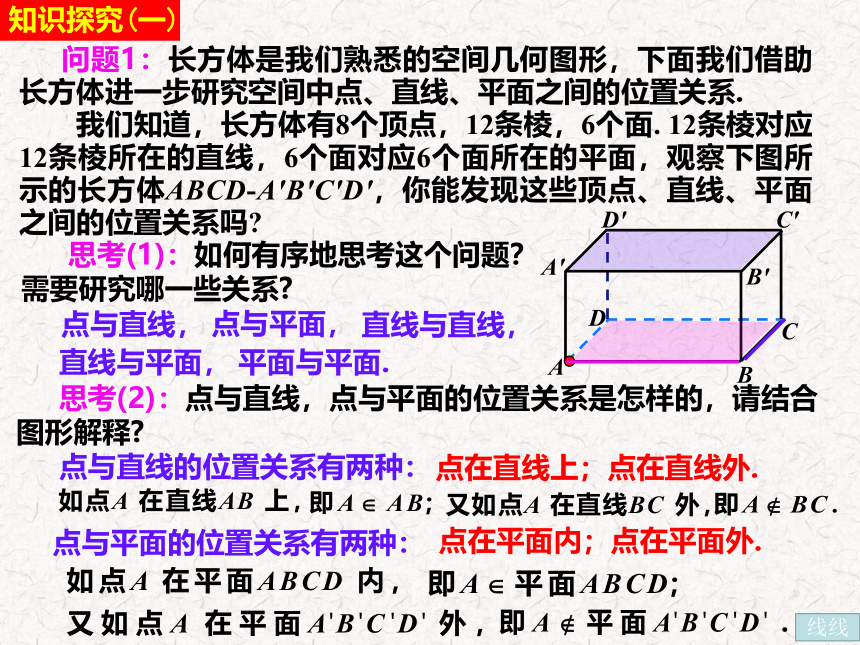
问题1:长方体是我们熟悉的空间几何图形,下面我们借助长方体进一步研究空间中点、直线、平面之间的位置关系.
我们知道,长方体有8个顶点,12条棱,6个面. 12条棱对应12条棱所在的直线,6个面对应6个面所在的平面,观察下图所示的长方体ABCD-A'B'C'D',你能发现这些顶点、直线、平面之间的位置关系吗
B
D
C
A'
B'
C'
D'
A
思考(1):如何有序地思考这个问题?需要研究哪一些关系
点与直线,
点与平面,
直线与直线,
直线与平面,
平面与平面.
思考(2):点与直线,点与平面的位置关系是怎样的,请结合图形解释
点与直线的位置关系有两种:
点在直线上;点在直线外.
点与平面的位置关系有两种:
点在平面内;点在平面外.
线线
B
D
C
A'
B'
C'
D'
A
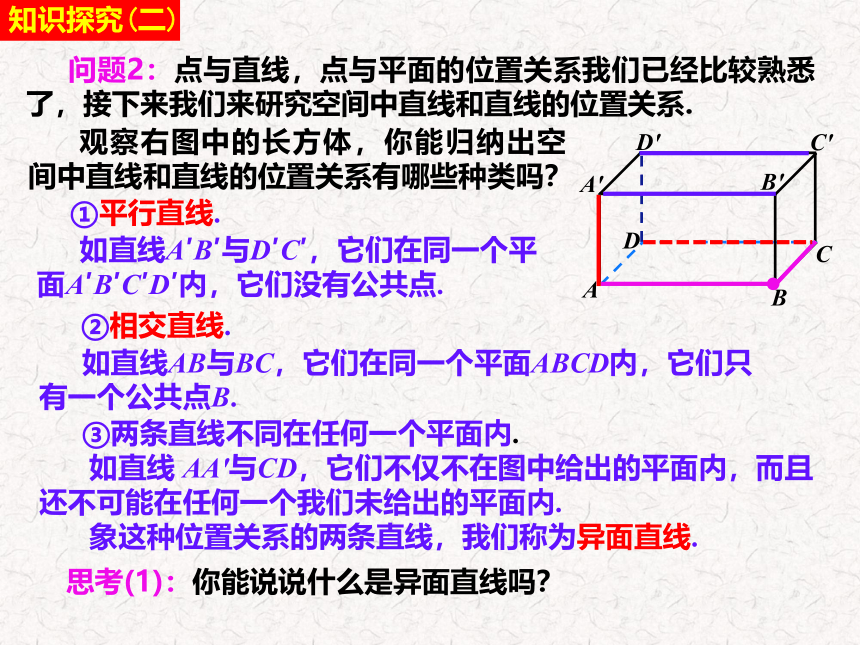
问题2:点与直线,点与平面的位置关系我们已经比较熟悉了,接下来我们来研究空间中直线和直线的位置关系.
知识探究(二)
观察右图中的长方体,你能归纳出空间中直线和直线的位置关系有哪些种类吗?
①平行直线.
如直线A′B′与D′C′,它们在同一个平面A′B′C′D′内,它们没有公共点.
②相交直线.
如直线AB与BC,它们在同一个平面ABCD内,它们只有一个公共点B.
③两条直线不同在任何一个平面内.
如直线 AA'与CD,它们不仅不在图中给出的平面内,而且还不可能在任何一个我们未给出的平面内.
象这种位置关系的两条直线,我们称为异面直线.
思考(1):你能说说什么是异面直线吗?
B
D
C
A'
B'
C'
D'
A
异面直线
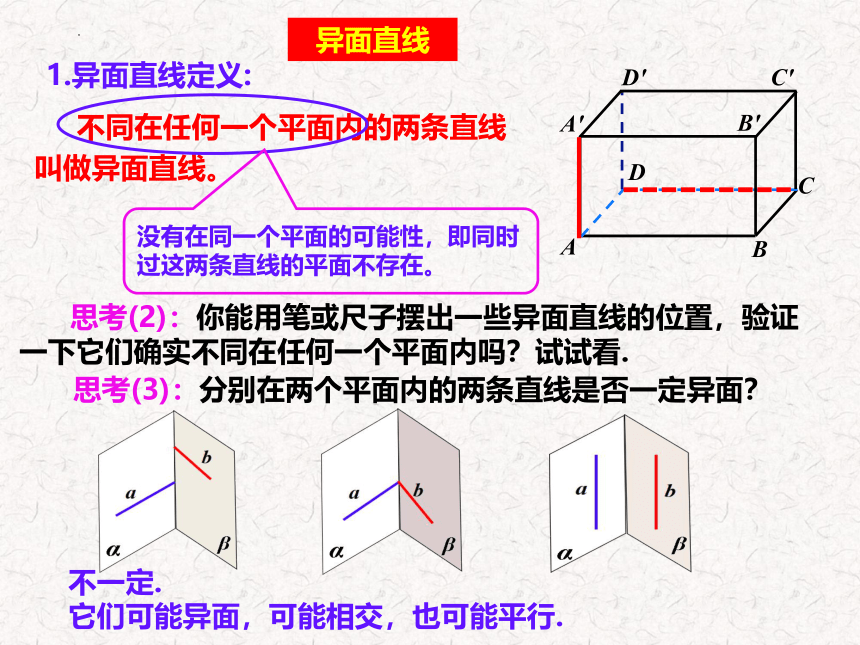
1.异面直线定义:
不同在任何一个平面内的两条直线叫做异面直线。
没有在同一个平面的可能性,即同时过这两条直线的平面不存在。
思考(3):分别在两个平面内的两条直线是否一定异面?
不一定.
它们可能异面,可能相交,也可能平行.
思考(2):你能用笔或尺子摆出一些异面直线的位置,验证一下它们确实不同在任何一个平面内吗?试试看.
B
D
C
A'
B'
C'
D'
A
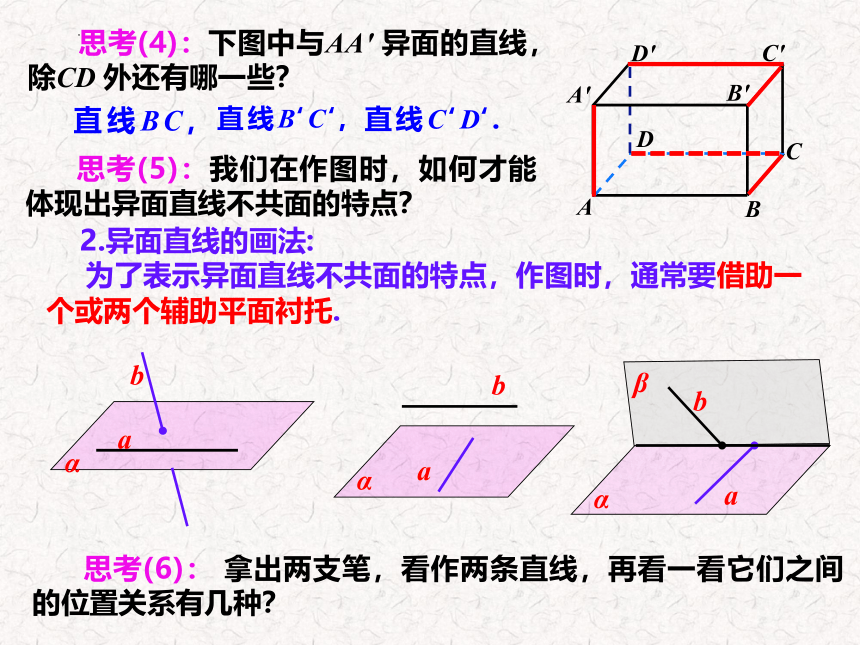
思考(4):下图中与AA' 异面的直线,除CD 外还有哪一些?
思考(5):我们在作图时,如何才能体现出异面直线不共面的特点?
2.异面直线的画法:
α
a
b
α
a
b
α
β
b
a
为了表示异面直线不共面的特点,作图时,通常要借助一个或两个辅助平面衬托.
思考(6): 拿出两支笔,看作两条直线,再看一看它们之间的位置关系有几种?
相交直线:
平行直线:
共面直线
异面直线:
不同在任何一个平面内,没有公共点
同一平面内, 有且只有一个公共点.
同一平面内,没有公共点.
1.根据两条直线是否共面分:
空间直线间的位置关系
2.根据两条直线公共点的个数分:
平行直线
异面直线
没有公共点
有且只有一个公共点:
相交直线
思考(7):我们根据前面的学习,你能给空间直线的位置关系作一个分类吗?你分类的标准是什么,结果又是怎样的?
线面
B
D
C
A'
B'
C'
D'
A
问题3:观察图中的长方体,类比问题2,你能完成空间中直线与平面位置关系的研究吗?
知识探究(三)
思考(1):回顾问题2的研究,你认为本题的研究路径是怎样的?
①直线在平面内.
如直线AB与平面ABCD内, 有无数个公共点,即
②直线与平面相交.
如直线AA′与平面ABCD相交于A,有1数公共点,即
观察长方体,举例说明直线与平面的关系
→举出更多实例
→用三种语言来表示
→按一定的标准来分类
思考(2):具体的过程和结果是怎样的?
③直线与平面平行.
如直线C′D′与平面ABCD平行, 没有公共点,即
→实验确认
拿出一本书和一支笔,看作一个平面和一条直线,看看它们之间的位置关系有几到底有几种?
由基本事实2可知,第二、三两种情况的直线都不在平面内,因此,直线与平面的位置关系可这样分:
空间直线与平面的位置关系
1.根据直线是否在平面内来分:
直线在平面内:
直线在平面外
直线与平面相交:
有1个公共点
直线与平面平行:
没有公共点
A
α
a
α
a
α
a
有无数个公共点
注意:
直线在平面内时,直线应全部画在平行四边形内;
直线在平面外时,直线应部分或全部画在平行四边形外
直线与平面有无数个公共点:
A
α
a
α
a
α
a
2.根据直线与平面公共点的个数来分:
直线在平面内
直线与平面有1个公共点:
直线与平面相交
直线与平面没有公共点:
直线与平面平行
面面
B
D
C
A'
B'
C'
D'
A
问题4:观察图中的长方体,类比前面的方法,你能完成空间中平面与平面位置关系的研究吗?
知识探究(四)
空间中平面与平面之间的位置关系
两个平面平行:
没有公共点
两个平面相交:
有一条公共直线
再拿出两本书,看作两个平面,上下、左右移动和翻转,看看它们之间的位置关系到底有几种?
平行,相交
返回
思考(1):直线与直线平行,直线与平面平行,平面与平面平行有什么相同之处?
都是没有公共点
思考(2):如图,长方体ABCD-A′B′C′D′中,连结A′B,CD′,请你再举一些空间中直线,平面之间位置关系的例子,并用符号语言表示出来?
B
D
C
A'
B'
C'
D'
A
例1.用符号表示下列图形中直线、平面之间的位置关系.
例析
思考:为了防止写漏,可以按照怎样的顺序来写?
例2.如图, AB∩α=B,A α,a α,B ∈a,直线AB 与 α 具有怎样的位置关系?为什么
思考(1):你能用穷举法说明这两直线不同在任一个平面吗?由此,你能想到什么方法来说明这个问题?
正难则反
可以先考虑它的反面(即两直线共面),会出现什么情况.
思考(2):由例2得到了一种判定两直线异面的方法,请说说这种方法?
与平面相交的直线和平面内不经过交点的直线异面.
结论
1.如果直线a,b没有公共点,那么a与b( ).
(A)共面 (B)平行 (C)异面 (D)可能平行,也可能异面
练习
2.设直线a,b分别是长方体相邻两个面的对角线所在的直线,
则a与b( ).
(A)共面 (B)相交 (C)异面 (D)可能相交,也可能异面
3.如图,在长方体ABCD-A′B′C′D′中,
请指出下列元素间的位置关系:
B
D
C
A'
B'
C'
D'
A
4.(1)经过同一直线上3个点的平面( ).
(A)有且仅有1个 (B)有且仅有3个 (C)有无数个 (D)不存在
(2)若直线a不平行平面α,且a α,则下列结论成立的是( ).
(A)α内的所有直线与a异面 (B)α内不存与a平行的直线
(C)α内存与惟一的直线与a平行
(D)α内的所有直线与a相交
1.本节课我们研究了什么问题?是按怎样的路径进行的?你从中获得哪一些知识?
课堂小结
2.通过本节课的学习?你获得了判定两直线异面的哪些方法?
3.通过本节(8.4)的学习?你对立体几何的学习方法有了哪一些新的认识,你认为长方体在立体几何的研究过程中有何作用?
立体几何的学习方法:
长方体是立体几何中的最重要模型之一,从中几乎可以找到点线面位置关系各种情况。
作业
8.4 空间点、直线、平面之间的关系
8.4.2 空间点、直线、平面的位置关系
复习与引入
前面我们认识了空间中点、直线、平面的一些位置关系,如点在平面内,直线在平面内,两个平面相交,等等.你还能想起这些关系吗?
图形语言 文字语言 符号语言
①
②
③
④
⑤
图形语言 文字语言 符号语言 ⑥ ⑦
⑧
那么空间中的点、直线、平面到底有怎样的位置关系吗 我们接下来就来探讨这个问题
知识探究(一)
问题1:长方体是我们熟悉的空间几何图形,下面我们借助长方体进一步研究空间中点、直线、平面之间的位置关系.
我们知道,长方体有8个顶点,12条棱,6个面. 12条棱对应12条棱所在的直线,6个面对应6个面所在的平面,观察下图所示的长方体ABCD-A'B'C'D',你能发现这些顶点、直线、平面之间的位置关系吗
B
D
C
A'
B'
C'
D'
A
思考(1):如何有序地思考这个问题?需要研究哪一些关系
点与直线,
点与平面,
直线与直线,
直线与平面,
平面与平面.
思考(2):点与直线,点与平面的位置关系是怎样的,请结合图形解释
点与直线的位置关系有两种:
点在直线上;点在直线外.
点与平面的位置关系有两种:
点在平面内;点在平面外.
线线
B
D
C
A'
B'
C'
D'
A
问题2:点与直线,点与平面的位置关系我们已经比较熟悉了,接下来我们来研究空间中直线和直线的位置关系.
知识探究(二)
观察右图中的长方体,你能归纳出空间中直线和直线的位置关系有哪些种类吗?
①平行直线.
如直线A′B′与D′C′,它们在同一个平面A′B′C′D′内,它们没有公共点.
②相交直线.
如直线AB与BC,它们在同一个平面ABCD内,它们只有一个公共点B.
③两条直线不同在任何一个平面内.
如直线 AA'与CD,它们不仅不在图中给出的平面内,而且还不可能在任何一个我们未给出的平面内.
象这种位置关系的两条直线,我们称为异面直线.
思考(1):你能说说什么是异面直线吗?
B
D
C
A'
B'
C'
D'
A
异面直线
1.异面直线定义:
不同在任何一个平面内的两条直线叫做异面直线。
没有在同一个平面的可能性,即同时过这两条直线的平面不存在。
思考(3):分别在两个平面内的两条直线是否一定异面?
不一定.
它们可能异面,可能相交,也可能平行.
思考(2):你能用笔或尺子摆出一些异面直线的位置,验证一下它们确实不同在任何一个平面内吗?试试看.
B
D
C
A'
B'
C'
D'
A
思考(4):下图中与AA' 异面的直线,除CD 外还有哪一些?
思考(5):我们在作图时,如何才能体现出异面直线不共面的特点?
2.异面直线的画法:
α
a
b
α
a
b
α
β
b
a
为了表示异面直线不共面的特点,作图时,通常要借助一个或两个辅助平面衬托.
思考(6): 拿出两支笔,看作两条直线,再看一看它们之间的位置关系有几种?
相交直线:
平行直线:
共面直线
异面直线:
不同在任何一个平面内,没有公共点
同一平面内, 有且只有一个公共点.
同一平面内,没有公共点.
1.根据两条直线是否共面分:
空间直线间的位置关系
2.根据两条直线公共点的个数分:
平行直线
异面直线
没有公共点
有且只有一个公共点:
相交直线
思考(7):我们根据前面的学习,你能给空间直线的位置关系作一个分类吗?你分类的标准是什么,结果又是怎样的?
线面
B
D
C
A'
B'
C'
D'
A
问题3:观察图中的长方体,类比问题2,你能完成空间中直线与平面位置关系的研究吗?
知识探究(三)
思考(1):回顾问题2的研究,你认为本题的研究路径是怎样的?
①直线在平面内.
如直线AB与平面ABCD内, 有无数个公共点,即
②直线与平面相交.
如直线AA′与平面ABCD相交于A,有1数公共点,即
观察长方体,举例说明直线与平面的关系
→举出更多实例
→用三种语言来表示
→按一定的标准来分类
思考(2):具体的过程和结果是怎样的?
③直线与平面平行.
如直线C′D′与平面ABCD平行, 没有公共点,即
→实验确认
拿出一本书和一支笔,看作一个平面和一条直线,看看它们之间的位置关系有几到底有几种?
由基本事实2可知,第二、三两种情况的直线都不在平面内,因此,直线与平面的位置关系可这样分:
空间直线与平面的位置关系
1.根据直线是否在平面内来分:
直线在平面内:
直线在平面外
直线与平面相交:
有1个公共点
直线与平面平行:
没有公共点
A
α
a
α
a
α
a
有无数个公共点
注意:
直线在平面内时,直线应全部画在平行四边形内;
直线在平面外时,直线应部分或全部画在平行四边形外
直线与平面有无数个公共点:
A
α
a
α
a
α
a
2.根据直线与平面公共点的个数来分:
直线在平面内
直线与平面有1个公共点:
直线与平面相交
直线与平面没有公共点:
直线与平面平行
面面
B
D
C
A'
B'
C'
D'
A
问题4:观察图中的长方体,类比前面的方法,你能完成空间中平面与平面位置关系的研究吗?
知识探究(四)
空间中平面与平面之间的位置关系
两个平面平行:
没有公共点
两个平面相交:
有一条公共直线
再拿出两本书,看作两个平面,上下、左右移动和翻转,看看它们之间的位置关系到底有几种?
平行,相交
返回
思考(1):直线与直线平行,直线与平面平行,平面与平面平行有什么相同之处?
都是没有公共点
思考(2):如图,长方体ABCD-A′B′C′D′中,连结A′B,CD′,请你再举一些空间中直线,平面之间位置关系的例子,并用符号语言表示出来?
B
D
C
A'
B'
C'
D'
A
例1.用符号表示下列图形中直线、平面之间的位置关系.
例析
思考:为了防止写漏,可以按照怎样的顺序来写?
例2.如图, AB∩α=B,A α,a α,B ∈a,直线AB 与 α 具有怎样的位置关系?为什么
思考(1):你能用穷举法说明这两直线不同在任一个平面吗?由此,你能想到什么方法来说明这个问题?
正难则反
可以先考虑它的反面(即两直线共面),会出现什么情况.
思考(2):由例2得到了一种判定两直线异面的方法,请说说这种方法?
与平面相交的直线和平面内不经过交点的直线异面.
结论
1.如果直线a,b没有公共点,那么a与b( ).
(A)共面 (B)平行 (C)异面 (D)可能平行,也可能异面
练习
2.设直线a,b分别是长方体相邻两个面的对角线所在的直线,
则a与b( ).
(A)共面 (B)相交 (C)异面 (D)可能相交,也可能异面
3.如图,在长方体ABCD-A′B′C′D′中,
请指出下列元素间的位置关系:
B
D
C
A'
B'
C'
D'
A
4.(1)经过同一直线上3个点的平面( ).
(A)有且仅有1个 (B)有且仅有3个 (C)有无数个 (D)不存在
(2)若直线a不平行平面α,且a α,则下列结论成立的是( ).
(A)α内的所有直线与a异面 (B)α内不存与a平行的直线
(C)α内存与惟一的直线与a平行
(D)α内的所有直线与a相交
1.本节课我们研究了什么问题?是按怎样的路径进行的?你从中获得哪一些知识?
课堂小结
2.通过本节课的学习?你获得了判定两直线异面的哪些方法?
3.通过本节(8.4)的学习?你对立体几何的学习方法有了哪一些新的认识,你认为长方体在立体几何的研究过程中有何作用?
立体几何的学习方法:
长方体是立体几何中的最重要模型之一,从中几乎可以找到点线面位置关系各种情况。
作业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
