苏教版小学数学五年级下册3.10《公倍数和最小公倍数》课件(共20张PPT)
文档属性
| 名称 | 苏教版小学数学五年级下册3.10《公倍数和最小公倍数》课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 286.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 13:30:39 | ||
图片预览

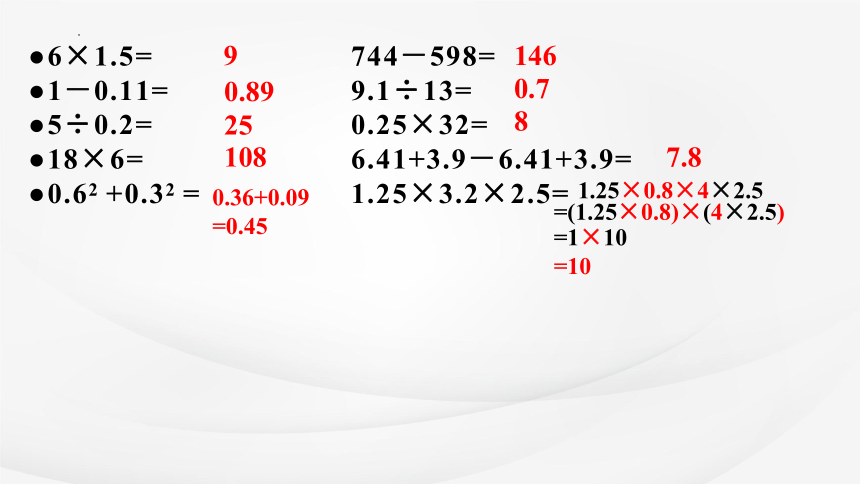






文档简介
(共20张PPT)
3.10 公倍数和最小公倍数2
6×1.5= 744-598=
1-0.11= 9.1÷13=
5÷0.2= 0.25×32=
18×6= 6.41+3.9-6.41+3.9=
0.62 +0.32 = 1.25×3.2×2.5=
9
146
0.89
0.7
25
8
108
7.8
0.36+0.09=0.45
1.25×0.8×4×2.5
=(1.25×0.8)×(4×2.5)
=1×10
=10
怎么找两个数的公倍数和最小公倍数?
列举法、筛选法(大数翻倍法)、短除法。
8 的倍数有_______________________;
20 的倍数有_______________________;
8 和 20 的公倍数有________________;
8 和 20 的最小公倍数是____________。
P46练习七 10.
8 , 16 , 24 , 32 , 40 , 48 , …
20 , 40 , 60 , 80 , 100 , …
40 , 80 , 120 , …
40
10、20、30、40、50、60、……
15的倍数有:
15、30、45、60、75、……
10和15的公倍数有:
30、60、90、……
10和15的最小公倍数是:
30
10的倍数有:
[10,15]= 30
你能用同样的方法找出 10和 15 的最小公倍数吗?
11. 找出每组数的最小公倍数。
6 和 10 8 和 12 10 和 25 20 和 30
[6,10]= 30
[8,12]= 24
[10,25]= 50
[20,30]= 60
10,20,30,40,50,……
12,24,36,48,……
25,50,75,100,……
30,60,90,120,……
(大数翻倍法)
12. 找出每组数的最小公倍数,想想它们的最小公倍数各有什么特点。
、
5和15 21和7
11和33 60和12
3和5 8和9
4和15 12和1
[5,15]= 15
[21,7]= 7
[11,33]= 11
[60,12]= 60
倍数关系,两个数的最小公倍数是较大的数。
[3,5]= 15
[8,9]= 72
[4,15]= 60
[12,1]= 12
互质关系,两个数的最小公倍数是它们的乘积。
13.直接写出下面每组数的最小公倍数。
7 和 10 4 和 9 8 和 24 27 和 3
互质关系
两个数的最小公倍数是它们的乘积。
倍数关系
两个数的最小公倍数是较大的数。
[7,10]= 70
[4,9]= 36
[8,24]= 24
[27,3]= 27
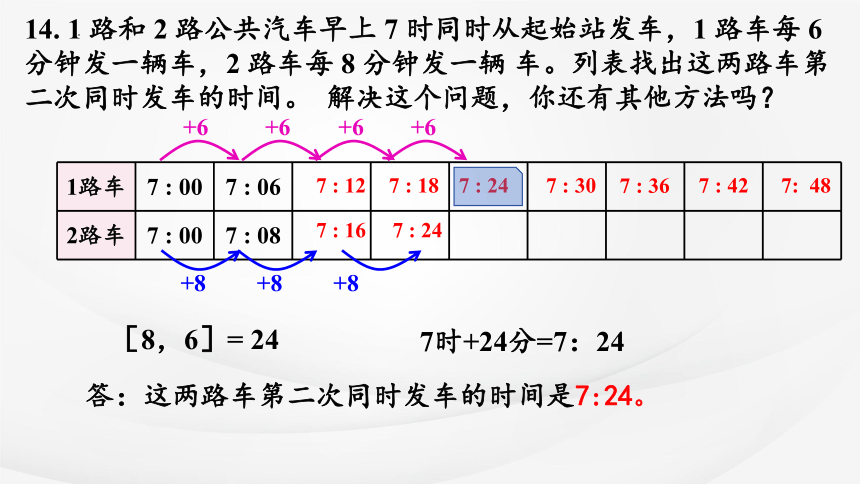
14. 1 路和 2 路公共汽车早上 7 时同时从起始站发车,1 路车每 6 分钟发一辆车,2 路车每 8 分钟发一辆 车。列表找出这两路车第二次同时发车的时间。 解决这个问题,你还有其他方法吗?
1路车 7 : 00 7 : 06
2路车 7 : 00 7 : 08
+6
+6
7 : 12
+6
7 : 18
+6
7 : 24
+8
+8
7 : 16
+8
7 : 24
7 : 30
7 : 36
7 : 42 7: 48
答:这两路车第二次同时发车的时间是7:24。
[8,6]= 24
7时+24分=7:24
填一填。
(1)两个自然数 a和b, a÷ b=5,那么 a和b的最小公倍数是( )。
(2)最小的质数和最小的合数的最大公因数是( ),最小公倍数是( )。
(3)一个数既是 3 的倍数,又是 5 和 7 的倍数,这个数最小是( )。
(4)如果a=2×3×5,b=3×5 ×7,那么a和b的最小公倍数是( )。
倍数关系,两个数的最小公倍数是较大的数。
a
2 4
2
4
3×5 ×7=105
105
3×5
3×5
3×5 ×2×7=210
210
1.一个两位数,既是6的倍数,又是10的倍数,这个两位数最小是( ), 最大是( )。
2.一包巧克力,无论分给6个人还是分给9个人,都正好分完。这包巧克力至少有( )块。
3.有两个数,它们的最大公因数是12,最小公倍数是72,这两个数是( ) 和( )或( )和( )
4.两个数的最大公因数是1,最小公倍数是24,这两个数是( )和( )或( )和( )。
30
90
[6,10]=30
[6,9]=18
12 72
24 36
1 24
3 8
选一选
(1)最小公倍数是35的一组数是( )。
A.5和7 B.3和35 C.15和25
(2) 42是6和7的( )。
A.公因数 B.最大公因数 C.公倍数
(3)两个数的积一定是它们的( )。
A.公因数 B.最小公倍数 C.公倍数
(4)两个数的最小公倍数( )。
A.比这两个数都大 B.一定等于较大的数
C.不会比大数小
A
C
C
C
[6,10]=30
[6,5]=30
[6,3]=6
欢欢和乐乐都利用暑假时间去游泳馆游泳,欢欢每3天去一次,乐乐每4天去一次,7月的最后一天两人正好同时去,最快( )月 ( )日他们又同时去。
如果是8月1日两人正好同时去,下一次( )月 ( )日他们又同时去。
[3,4]=12
8 12
1+12=13
8 13
拓展1五年级学生参加植树活动,人数在 40~50 之间。如果分成 4 人一组或者 6 人一组,都恰好分完。五年级参加植树活动的有多少人
4和6的公倍数有 12,24,36,48,……。
答:五年级参加植树活动的有 48 人。
拓展2 从运动场一端到另一端全长 96 米,从一端起到另一端每隔 4 米插一面小红旗(两端都要插),现在改为每隔 6 米插一面小红旗,有多少面小红旗不用移动
[4, 6 ]=12
96÷12 +1=9(面)
答:有9面小红旗不用移动。
拓展3 一种砖长 22 厘米,宽 10 厘米,要铺成一个正方形地面(不折断,只能铺整砖),至少要铺多少块砖
[22,10]=110
110÷22=5( 块)
110÷10=11( 块)
5 × 11=55( 块)
答:至少要铺 55 块砖。
拓展4 一个电子钟,每到整点响一次铃,每走 24 分钟亮一次灯,上午 8 时,它既响铃又亮灯了下一次既响铃又亮灯是什么时候
[60, 24]=120
上午8 时再过120分钟即2 小时是上午 10时,故下一次既响铃又亮灯是上午 10时。
1.学校运来--批树苗,如果每行栽8棵或每行栽10棵,都恰好能栽成整行数。这批树苗至少有多少棵
[8,10]=40
答:这批树苗至少有40棵。
2.一种长方形地砖长40厘米.宽30厘米,用这种地砖正好可以铺满一个正方形地面,地砖不可切割。这个正方形地面的边长最小是多少厘米 至少需要多少块这种地砖
[40,30]=2×5×3×4=120
答:这个正方形地面的边长最小是120厘米,至少需要12块这种地砖。
40 30
2
5
20 15
4 3
长 宽
120÷40=3(块)
120÷30=4(块)
4×3=12(块)
比一比,算一算。
1.将一张长16厘米、宽12厘米的长方形纸,裁成同样大小、面积尽可能大的正方形,且纸没有剩余。这个正方形的边长最大是多少厘米?可以裁成多少个这样的正方形
2.有一些长16厘米.宽12厘米的长方形,要把它们拼成一个大正方形。这个正方形的边长最小是多少厘米?至少需要多少个这样的长方形
3.10 公倍数和最小公倍数2
6×1.5= 744-598=
1-0.11= 9.1÷13=
5÷0.2= 0.25×32=
18×6= 6.41+3.9-6.41+3.9=
0.62 +0.32 = 1.25×3.2×2.5=
9
146
0.89
0.7
25
8
108
7.8
0.36+0.09=0.45
1.25×0.8×4×2.5
=(1.25×0.8)×(4×2.5)
=1×10
=10
怎么找两个数的公倍数和最小公倍数?
列举法、筛选法(大数翻倍法)、短除法。
8 的倍数有_______________________;
20 的倍数有_______________________;
8 和 20 的公倍数有________________;
8 和 20 的最小公倍数是____________。
P46练习七 10.
8 , 16 , 24 , 32 , 40 , 48 , …
20 , 40 , 60 , 80 , 100 , …
40 , 80 , 120 , …
40
10、20、30、40、50、60、……
15的倍数有:
15、30、45、60、75、……
10和15的公倍数有:
30、60、90、……
10和15的最小公倍数是:
30
10的倍数有:
[10,15]= 30
你能用同样的方法找出 10和 15 的最小公倍数吗?
11. 找出每组数的最小公倍数。
6 和 10 8 和 12 10 和 25 20 和 30
[6,10]= 30
[8,12]= 24
[10,25]= 50
[20,30]= 60
10,20,30,40,50,……
12,24,36,48,……
25,50,75,100,……
30,60,90,120,……
(大数翻倍法)
12. 找出每组数的最小公倍数,想想它们的最小公倍数各有什么特点。
、
5和15 21和7
11和33 60和12
3和5 8和9
4和15 12和1
[5,15]= 15
[21,7]= 7
[11,33]= 11
[60,12]= 60
倍数关系,两个数的最小公倍数是较大的数。
[3,5]= 15
[8,9]= 72
[4,15]= 60
[12,1]= 12
互质关系,两个数的最小公倍数是它们的乘积。
13.直接写出下面每组数的最小公倍数。
7 和 10 4 和 9 8 和 24 27 和 3
互质关系
两个数的最小公倍数是它们的乘积。
倍数关系
两个数的最小公倍数是较大的数。
[7,10]= 70
[4,9]= 36
[8,24]= 24
[27,3]= 27
14. 1 路和 2 路公共汽车早上 7 时同时从起始站发车,1 路车每 6 分钟发一辆车,2 路车每 8 分钟发一辆 车。列表找出这两路车第二次同时发车的时间。 解决这个问题,你还有其他方法吗?
1路车 7 : 00 7 : 06
2路车 7 : 00 7 : 08
+6
+6
7 : 12
+6
7 : 18
+6
7 : 24
+8
+8
7 : 16
+8
7 : 24
7 : 30
7 : 36
7 : 42 7: 48
答:这两路车第二次同时发车的时间是7:24。
[8,6]= 24
7时+24分=7:24
填一填。
(1)两个自然数 a和b, a÷ b=5,那么 a和b的最小公倍数是( )。
(2)最小的质数和最小的合数的最大公因数是( ),最小公倍数是( )。
(3)一个数既是 3 的倍数,又是 5 和 7 的倍数,这个数最小是( )。
(4)如果a=2×3×5,b=3×5 ×7,那么a和b的最小公倍数是( )。
倍数关系,两个数的最小公倍数是较大的数。
a
2 4
2
4
3×5 ×7=105
105
3×5
3×5
3×5 ×2×7=210
210
1.一个两位数,既是6的倍数,又是10的倍数,这个两位数最小是( ), 最大是( )。
2.一包巧克力,无论分给6个人还是分给9个人,都正好分完。这包巧克力至少有( )块。
3.有两个数,它们的最大公因数是12,最小公倍数是72,这两个数是( ) 和( )或( )和( )
4.两个数的最大公因数是1,最小公倍数是24,这两个数是( )和( )或( )和( )。
30
90
[6,10]=30
[6,9]=18
12 72
24 36
1 24
3 8
选一选
(1)最小公倍数是35的一组数是( )。
A.5和7 B.3和35 C.15和25
(2) 42是6和7的( )。
A.公因数 B.最大公因数 C.公倍数
(3)两个数的积一定是它们的( )。
A.公因数 B.最小公倍数 C.公倍数
(4)两个数的最小公倍数( )。
A.比这两个数都大 B.一定等于较大的数
C.不会比大数小
A
C
C
C
[6,10]=30
[6,5]=30
[6,3]=6
欢欢和乐乐都利用暑假时间去游泳馆游泳,欢欢每3天去一次,乐乐每4天去一次,7月的最后一天两人正好同时去,最快( )月 ( )日他们又同时去。
如果是8月1日两人正好同时去,下一次( )月 ( )日他们又同时去。
[3,4]=12
8 12
1+12=13
8 13
拓展1五年级学生参加植树活动,人数在 40~50 之间。如果分成 4 人一组或者 6 人一组,都恰好分完。五年级参加植树活动的有多少人
4和6的公倍数有 12,24,36,48,……。
答:五年级参加植树活动的有 48 人。
拓展2 从运动场一端到另一端全长 96 米,从一端起到另一端每隔 4 米插一面小红旗(两端都要插),现在改为每隔 6 米插一面小红旗,有多少面小红旗不用移动
[4, 6 ]=12
96÷12 +1=9(面)
答:有9面小红旗不用移动。
拓展3 一种砖长 22 厘米,宽 10 厘米,要铺成一个正方形地面(不折断,只能铺整砖),至少要铺多少块砖
[22,10]=110
110÷22=5( 块)
110÷10=11( 块)
5 × 11=55( 块)
答:至少要铺 55 块砖。
拓展4 一个电子钟,每到整点响一次铃,每走 24 分钟亮一次灯,上午 8 时,它既响铃又亮灯了下一次既响铃又亮灯是什么时候
[60, 24]=120
上午8 时再过120分钟即2 小时是上午 10时,故下一次既响铃又亮灯是上午 10时。
1.学校运来--批树苗,如果每行栽8棵或每行栽10棵,都恰好能栽成整行数。这批树苗至少有多少棵
[8,10]=40
答:这批树苗至少有40棵。
2.一种长方形地砖长40厘米.宽30厘米,用这种地砖正好可以铺满一个正方形地面,地砖不可切割。这个正方形地面的边长最小是多少厘米 至少需要多少块这种地砖
[40,30]=2×5×3×4=120
答:这个正方形地面的边长最小是120厘米,至少需要12块这种地砖。
40 30
2
5
20 15
4 3
长 宽
120÷40=3(块)
120÷30=4(块)
4×3=12(块)
比一比,算一算。
1.将一张长16厘米、宽12厘米的长方形纸,裁成同样大小、面积尽可能大的正方形,且纸没有剩余。这个正方形的边长最大是多少厘米?可以裁成多少个这样的正方形
2.有一些长16厘米.宽12厘米的长方形,要把它们拼成一个大正方形。这个正方形的边长最小是多少厘米?至少需要多少个这样的长方形
