2015年秋高中数学北师大版必修五课件:2三角形中的几何计算(共12张PPT)
文档属性
| 名称 | 2015年秋高中数学北师大版必修五课件:2三角形中的几何计算(共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 741.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-08 14:27:37 | ||
图片预览




文档简介
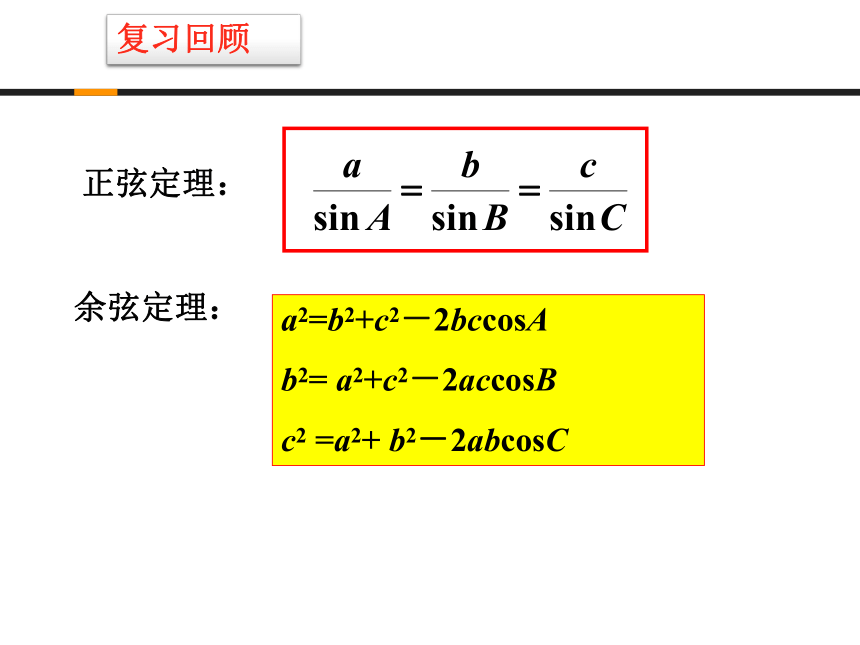
课件12张PPT。第二章 解三角形2 三角形中的几何计算 正弦定理:a2=b2+c2-2bccosA
b2= a2+c2-2accosB
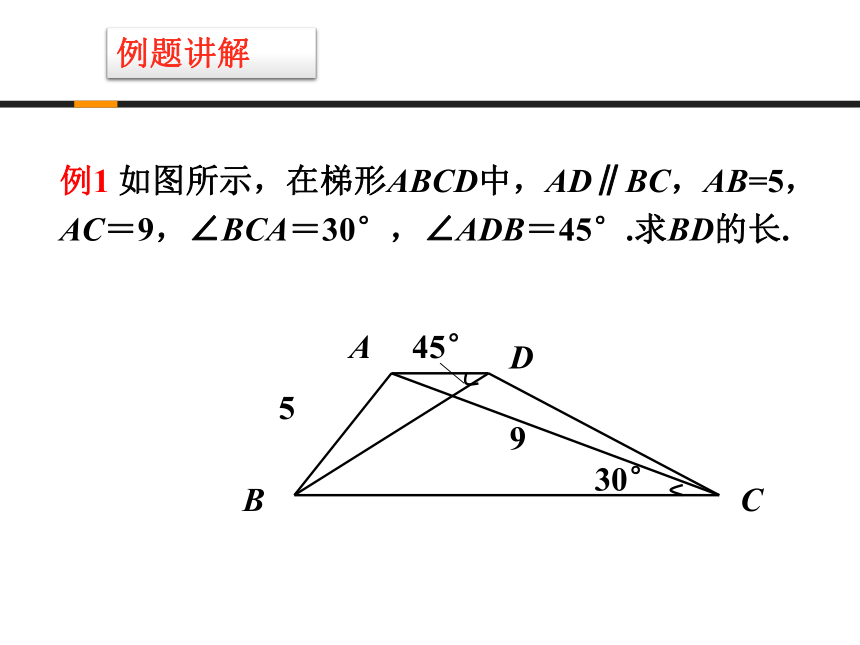
c2 =a2+ b2-2abcosC 余弦定理:复习回顾三角形面积公式:复习回顾例题讲解例1 如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.求BD的长.解 在ΔABC中, AB=5,AC=9,∠BCA=30°.由正弦定理,得因为AD∥BC,所以∠BAD=180 °-∠ABC同理,在ΔABD中, AB=5, ∠ADB=45°例题讲解例2 一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度像点A作匀速直线滚动.如图所示,已知
若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?例题讲解分析 机器人最快截住足球的地方正式机器人与足球同时到达的地方,设为C点.利用速度建立AC与BC之间的 关系,再利用余弦定理便可建立方程解决问题.例题讲解解 设该机器人最快可在点C处截住足球,点C在线段AD上,设BC=x dm,由题意,CD=2x dm
AC=AD-CD=(17-2x) dm在ΔABC中,由余弦定理得例题讲解例题讲解例题讲解 例4 如图 设A、B两点都在河的对岸(不可到达),设计一种测量A、B两点间距离的方法.例题讲解 解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得
b2= a2+c2-2accosB
c2 =a2+ b2-2abcosC 余弦定理:复习回顾三角形面积公式:复习回顾例题讲解例1 如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.求BD的长.解 在ΔABC中, AB=5,AC=9,∠BCA=30°.由正弦定理,得因为AD∥BC,所以∠BAD=180 °-∠ABC同理,在ΔABD中, AB=5, ∠ADB=45°例题讲解例2 一次机器人足球比赛中,甲队1号机器人由点A开始作匀速直线运动,到达点B时,发现足球在点D处正以2倍于自己的速度像点A作匀速直线滚动.如图所示,已知
若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?例题讲解分析 机器人最快截住足球的地方正式机器人与足球同时到达的地方,设为C点.利用速度建立AC与BC之间的 关系,再利用余弦定理便可建立方程解决问题.例题讲解解 设该机器人最快可在点C处截住足球,点C在线段AD上,设BC=x dm,由题意,CD=2x dm
AC=AD-CD=(17-2x) dm在ΔABC中,由余弦定理得例题讲解例题讲解例题讲解 例4 如图 设A、B两点都在河的对岸(不可到达),设计一种测量A、B两点间距离的方法.例题讲解 解:测量者可以在河岸边选定两点C、D,测得CD=a,并且在C、D两点分别测得
