必考小专题:比例综合-数学六年级下册北师大版(含答案)
文档属性
| 名称 | 必考小专题:比例综合-数学六年级下册北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 727.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
必考小专题:比例综合-数学六年级下册北师大版
1.酸梅汤是夏季防暑去火的上佳饮品。林阿姨多次尝试,发现用60毫升的酸梅原汁和140毫升的水配制的酸梅汤口感最佳。现在林阿姨打算配制3600毫升同样口感的酸梅汤,需要酸梅原汁多少毫升?
2.在一幅比例尺是1∶6000000的地图上,量得甲、乙两地之间的距离大约是7厘米,一辆客车和一辆货车同时从甲、乙两地出发,相向而行,3小时相遇,已知客车和货车的速度比是4∶3,客车、货车的速度各是多少?
3.A地到C地的高速公路经过B地,全程距离大约为440千米,A地到B地大约为120千米。一辆汽车从A地出发开往C地,当行驶到B地时用了1.5小时。按照这个速度,A地到C地全程需要多少小时?(用比例解题)
4.科学家往往具有非凡的毅力和不懈探索的精神,居里夫人从24吨废矿渣里才提炼出0.1克镭。照这样计算,要提炼1.5克镭,需要多少吨这样的废矿渣?(用比例解答)
5.甲、乙两地之间的高速铁路大约长1600千米。丙地在甲地、乙地之间甲地到丙地的高速铁路大约长700千米。一列由甲地开往乙地的高铁列车9:00出发,11:30到达丙地。按照这样的平均速度,6小时能从甲地到乙地吗?
6.为创建全国文明城市,阳城公园种了一块三角形的草坪,在比例尺1∶8000的平面图上量得这块草坪的底是2.5厘米,高是0.4厘米。这块三角形草地的实际面积是多少?
7.李老师家装修新房,计划用边长是0.8米的正方形瓷砖铺客厅地面,这样需要40块;后来改为面积是0.8平方米的正方形瓷砖铺地,需要多少块?(列比例解答)
8.电动车厂原计划每天生产电动车400辆,25天可以完成任务,实际每天生产500辆,实际多少天可以完成任务?(用比例解)
9.李师傅计划加工一批零件,前五天加工了120个,照这样计算,再用18天就可以做完,这批零件一共有多少个?(用比例解)
10.一列火车从甲地开往乙地,9小时行驶720千米。照这样的速度,行驶完全程960km,一共需要多少小时?(用比例解)
11.博物馆展出一个高为18.2厘米的秦代将军俑模型,它的高度与实际高度的比是1∶10。这个将军俑的实际高度是多少厘米?
12.小丽在太阳下某一位置测得自己的影长是1.2米,在同一时间同一地点把20分米长的竹竿立在地上,测得竹竿的影长是15分米,小丽的身高是多少米?(用比例解)
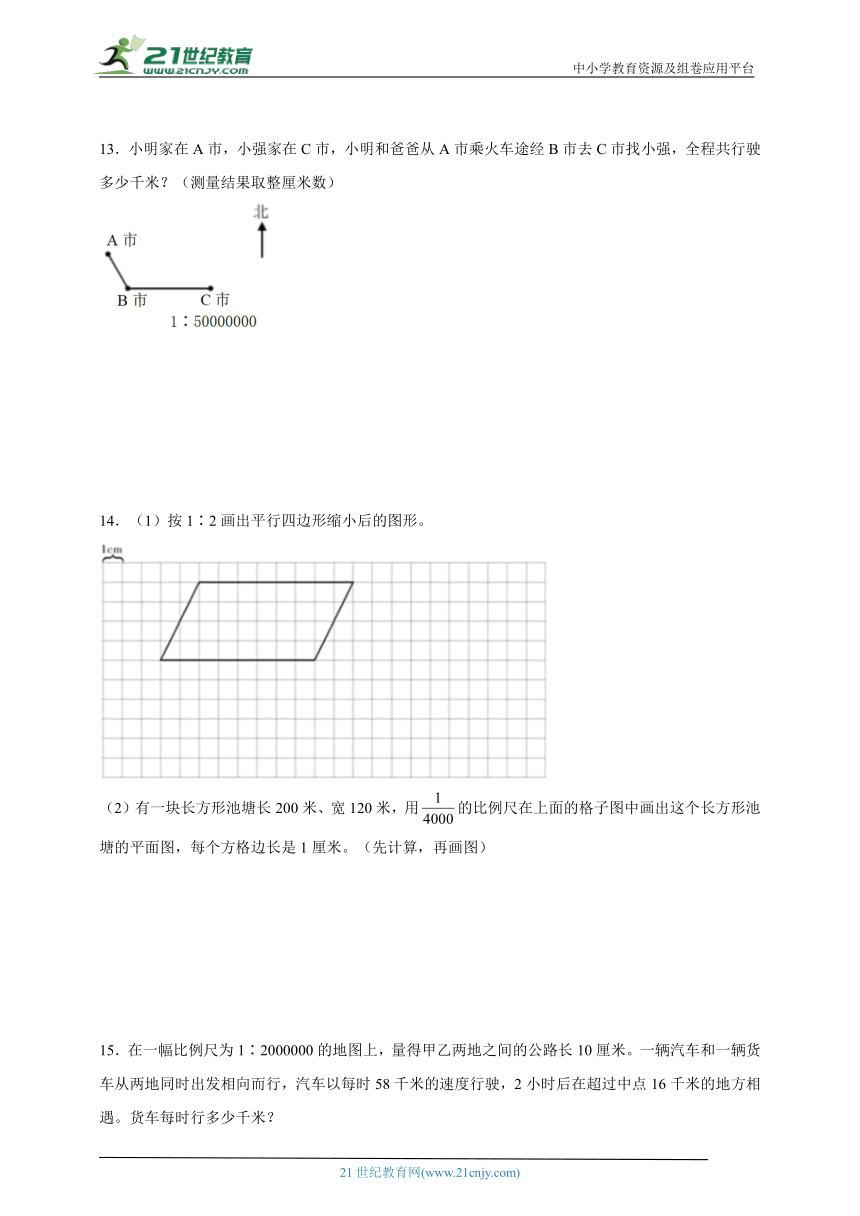
13.小明家在A市,小强家在C市,小明和爸爸从A市乘火车途经B市去C市找小强,全程共行驶多少千米?(测量结果取整厘米数)
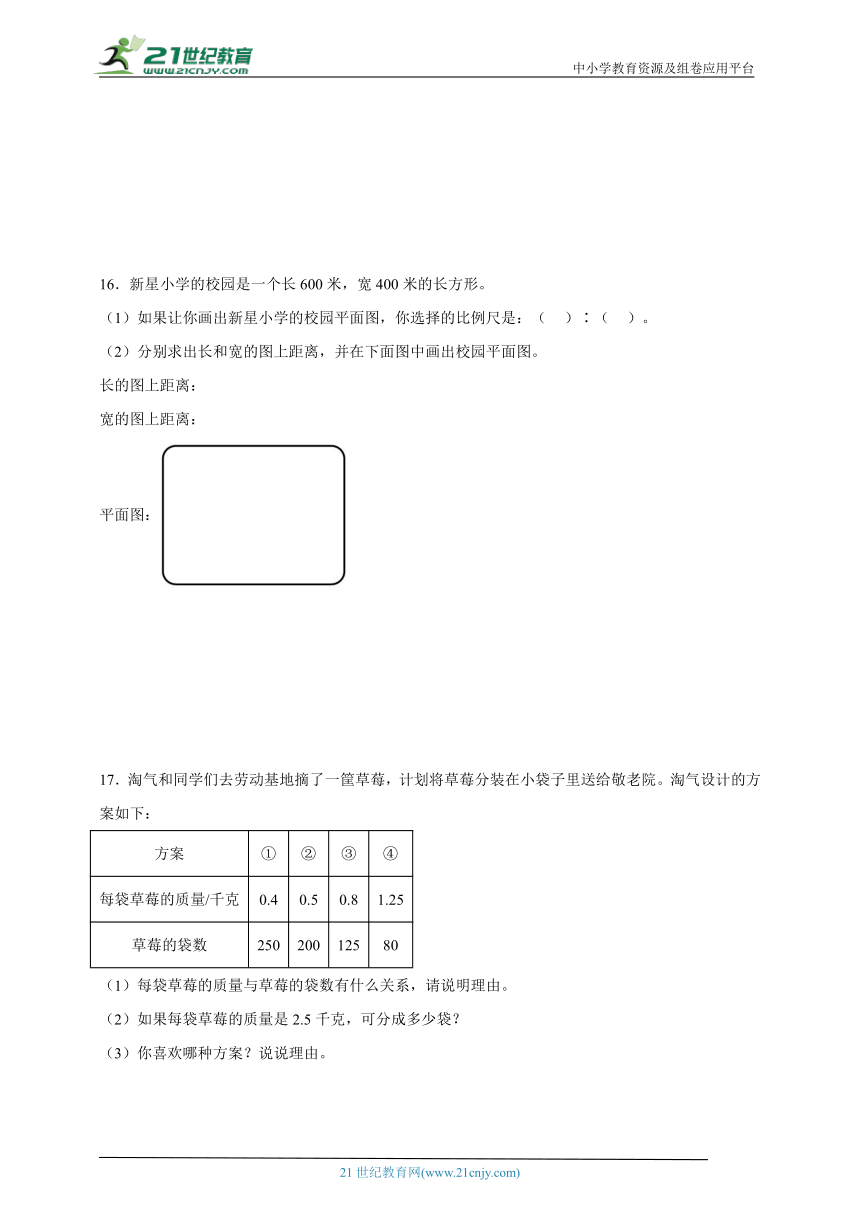
14.(1)按1∶2画出平行四边形缩小后的图形。
(2)有一块长方形池塘长200米、宽120米,用的比例尺在上面的格子图中画出这个长方形池塘的平面图,每个方格边长是1厘米。(先计算,再画图)
15.在一幅比例尺为1∶2000000的地图上,量得甲乙两地之间的公路长10厘米。一辆汽车和一辆货车从两地同时出发相向而行,汽车以每时58千米的速度行驶,2小时后在超过中点16千米的地方相遇。货车每时行多少千米?
16.新星小学的校园是一个长600米,宽400米的长方形。
(1)如果让你画出新星小学的校园平面图,你选择的比例尺是:( )∶( )。
(2)分别求出长和宽的图上距离,并在下面图中画出校园平面图。
长的图上距离:
宽的图上距离:
平面图:
17.淘气和同学们去劳动基地摘了一筐草莓,计划将草莓分装在小袋子里送给敬老院。淘气设计的方案如下:
方案 ① ② ③ ④
每袋草莓的质量/千克 0.4 0.5 0.8 1.25
草莓的袋数 250 200 125 80
(1)每袋草莓的质量与草莓的袋数有什么关系,请说明理由。
(2)如果每袋草莓的质量是2.5千克,可分成多少袋?
(3)你喜欢哪种方案?说说理由。
18.一辆汽车的行驶的路程和所需的时间如下表。
时间(时) 1 2 3 4 5 6
路程(千米) 60 120 180 240
(1)把上表填写完整。
(2)这辆汽车行驶的路程和所需的时间是否成正比例,请说明理由。
(3)根据上表描点,再顺次连接各点,你发现了什么?
(4)点(9,540)在这条直线上吗?这一点表示什么含意?
19.一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/千米 80 160 240 320 400 480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。说一说这个比值表示什么。
(2)汽车行驶的路程与时间成正比例关系还是反比例关系?为什么?
(3)在图中描出表示路程和相对应时间的点,然后把它们按顺序连起来。并估计一下行200千米大约需要多少时间。
20.下面是公园街区的平面示意图。
(1)广场在公园( )偏( )30°方向上,实际距离是( )米。
(2)喷水池在广场西南方向750米处,请在图上画出位置用点标明。
21.填一填,画一画。
(1)用数对表示A,C两点的位置:A( ),C( )。
(2)画出图中的三角形ABC绕B点顺时针旋转90°后的图形。
(3)画出图中的三角形ABC按3∶1放大后的图形。
参考答案:
1.1080毫升
【分析】由信息“60毫升的酸梅原汁和140毫升的水配制酸梅汤,口感最佳”可知,酸梅与水的比是一定的,根据此列出方程解答。设需要酸梅x毫升,那么水就有(3600-x)毫升,根据酸梅:水的比一定列出比例:x∶(3600-x)=60∶140,解比例即可。
【详解】解:设需要酸梅x毫升,那么水就有(3600-x)毫升。
x∶(3600-x)=60∶140
140x=60×(3600-x)
140x=216000-60x
140x+60x=21600
200x=216000
x=216000÷200
x=1080
答:需要酸梅原汁毫升1080毫升。
【点睛】解答此题关键找出酸梅的浓度不变,据此设出未知数,找出相关的量,列比例解答即可。
2.客车80千米/时,货车60千米/时
【分析】根据实际距离=图上距离÷比例尺,据此求出甲、乙两地的实际距离,再根据相遇问题中,相遇路程÷相遇时间=速度和,据此求出客车和货车的速度和,再根据按比分配问题求出客车、货车的速度即可。
【详解】7÷=42000000(厘米)=420(千米)
420÷3×
=140×
=80(千米/时)
420÷3×
=140×
=60(千米/时)
答:客车的速度是80千米/时,货车的速度是60千米/时。
【点睛】本题考查比例尺,明确图上距离、实际距离和比例尺之间的关系是解题的关键。
3.5.5小时
【分析】由题意可知,汽车的速度不变,则路程和时间成正比例关系,路程÷时间=速度(一定),把行完全程需要的时间设为未知数,A地到C地的路程∶A地到C地的时间=A地到B地的路程∶A地到B地的时间,据此解答。
【详解】解:设A地到C地全程需要x小时。
440∶x=120∶1.5
120x=440×1.5
120x=660
x=660÷120
x=5.5
答:A地到C地全程需要5.5小时。
【点睛】本题主要考查应用比例解决实际问题,理解速度一定时,路程与时间成正比例是解答题目的关键。
4.360吨
【分析】由题意可知,提炼每克镭需要废矿渣的质量不变,则需要废矿渣的质量和镭的质量成正比例关系,需要废矿渣的质量∶提炼镭的质量=24∶0.1,据此列方程解答。
【详解】解:设需要吨这样的废矿渣。
答:需要360吨这样的废矿渣。
【点睛】本题主要考查比例的应用,明确两种相关联的量成正比例关系是解答题目的关键。
5.能
【分析】根据题意可知,甲地到丙地需要2.5小时,根据速度=路程÷时间,速度一定,则路程和时间成正比例,假设甲地到乙地需要x小时,列方程为1600∶x=700∶2.5,然后解出方程,最后和6小时比较即可。
【详解】11:30-9:00=2小时30分钟
2小时30分钟=2.5小时
解:设甲地到乙地需要x小时。
1600∶x=700∶2.5
700x=1600×2.5
700x=4000
x=4000÷700
x=
<6
答:6小时能从甲地到乙地。
【点睛】本题主要考查了正比例的应用,找到相应的数量关系式是解答本题的关键。
6.3200平方米
【分析】根据实际距离=图上距离÷比例尺,据此求出这块草坪的底和高的实际长度,再根据三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】2.5÷=20000(厘米)=200(米)
0.4÷=3200(厘米)=32(米)
200×32÷2
=6400÷2
=3200(平方米)
答:这块三角形草地的实际面积是3200平方米。
【点睛】本题考查比例尺,结合三角形的面积的计算方法是解题的关键。
7.32块
【分析】根据题意可知,每块正方形瓷砖的面积×块数=客厅地面的面积(一定),积一定,那么每块正方形瓷砖的面积与块数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设需要块。
0.8=0.8×0.8×40
0.8=25.6
=25.6÷0.8
=32
答:需要32块。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
8.20天
【分析】设实际x天可以完成任务,根据每天生产数量×天数=总数量(一定),列出反比例算式解答即可。
【详解】解:设实际x天可以完成任务。
500x=400×25
500x=10000
500x÷500=10000÷500
x=20
答:实际20天可以完成任务。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
9.552个
【分析】根据题意知道,工作效率一定,工作量和工作时间成正比例,由此列式解答即可。
【详解】解:设这批零件一共有x个,则:
x∶(5+18)=120∶5
x∶23=120∶5
5x=120×23
5x=2760
5x÷5=2760÷5
x=552
答:这批零件一共有552个。
【点睛】解答此题的关键是判断哪两种量成何比例,然后找准对应量,列式解答即可。
10.12小时
【分析】这个题目中速度是一定的,路程÷时间=速度。
【详解】解:设一共需要小时
960∶=720∶9
720=960×9
=12
答:一共需要12小时。
【点睛】能够知道题目中哪个量是不变的,知道已知两个量的关系是正比例关系还是反比例关系。
11.182厘米
【分析】根据题意可知,秦代将军俑模型的高度∶实际高度=1∶10,比值一定,秦代将军俑模型的高度和实际高度成正比例,设这个将军俑的实际高度是x厘米,列方程为18.2∶x=1∶10,然后解出方程即可。
【详解】解:设这个将军俑的实际高度是x厘米。
18.2∶x=1∶10
x=18.2×10
x=182
答:这个将军俑的实际高度是182厘米。
【点睛】本题考查了正比例的认识和应用,可列方程解决问题。
12.1.6米
【分析】同一时间同一地点,竿高和影长成正比例,即,据此等量关系列出比例解答即可。
【详解】20分米=2米
15分米=1.5米
解:设小丽的身高是x米。
x∶1.2=2∶1.5
1.5x=1.2×2
1.5x=2.4
x=2.4÷1.5
x=1.6
答:小丽的身高是1.6米。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
13.1500千米
【分析】先量出从A市途经B市到C市的图上距离,再根据“图上距离÷比例尺=实际距离”解答即可。
【详解】(1+2)÷
=3÷
=3×50000000
=150000000(厘米)
150000000厘米=1500千米
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
14.(1)见详解;
(2)长5厘米;宽3厘米;图形见详解
【分析】(1)原来平行四边形的底边为8厘米,缩小后对应的底边为8×=4(厘米),原来平行四边形的高为4厘米,缩小后对应的高为4×=2(厘米),平行四边形缩小以后形状不变,只是位置和大小发生了变化;
(2)根据“图上距离=实际距离×比例尺”分别计算出这个长方形池塘在格子图中的长和宽,再根据计算结果画出长方形池塘的平面图,据此解答。
【详解】(1)分析可知:
(2)200米=20000厘米
120米=12000厘米
长:20000×=5(厘米)
宽:12000×=3(厘米)
作图如下:
【点睛】掌握缩小图形的作图方法以及图上距离和实际距离换算的方法是解答题目的关键。
15.42千米
【分析】根据“实际距离=图上距离÷比例尺”求出甲乙两地之间的实际距离,再利用速度和=总路程÷相遇时间求出汽车和货车的速度和,最后用减法求出货车的速度,据此解答。
【详解】10÷=20000000(厘米)
20000000厘米=200千米
200÷2-58
=100-58
=42(千米)
答:货车每时行42千米。
【点睛】本题考查比例尺,求出甲乙两地的实际距离是解题的关键。
16.(1)1∶20000
(2)见详解
【分析】(1)图上距离∶实际距离=比例尺,据此确定比例尺;
(2)图上距离=实际距离×比例尺,据此求出图上距离,作图即可。
【详解】(1)选择的比例尺是:1∶20000。
(2)600米=60000厘米
400米=40000厘米
长的图上距离:60000×=3(厘米)
宽的图上距离:40000×=2(厘米)
(答案不唯一)
【点睛】关键是理解比例尺的意义,掌握图上距离与实际距离的换算方法。
17.(1)反比例,因为每袋草莓的质量与草莓的袋数的乘积一定;(2)40袋;(3)第④个,因为袋数比较少,同学们比较好拿
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。观察表格可知,每袋草莓的质量和草莓的袋数的乘积一定,所以它们成反比例;
(2)根据每袋草莓的质量×草莓的袋数=总质量,用总质量除以2.5千克,即可求出草莓的袋数;
(3)给出的理由合理即可。
【详解】(1)0.4×250=100(千克)
0.5×200=100(千克)
0.8×125=100(千克)
1.25×80=100(千克)
每袋草莓的质量和草莓的袋数的乘积一定,所以它们成反比例。
(2)100÷2.5=40(袋)
答:如果每袋草莓的质量是2.5千克,可分成40袋。
(3)我喜欢第④个方案,因为袋数比较少,同学们比较好拿。(答案不唯一)
【点睛】本题主要考查了反比例的意义和辨识。
18.(1)见详解
(2)成正比例,理由见详解
(3)这辆汽车行驶的路程和所需的时间形成的图像是一条直线
(4)在,这一点表示汽车9小时行驶了540千米
【分析】(1)根据路程÷时间=速度,60÷1=60,120÷2=60,据此发现汽车的速度是一定的,再根据速度×时间=路程,据此计算并填空即可;
(2)两个相关联的量,若它们的比值一定,则它们成正比例;若它们的乘积一定,则它们成反比例;
(3)根据统计表上的数据在统计图上描出各点,再顺次连接各点,最后再观察即可;
(4)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,也就是横轴表示时间,纵轴表示路程,据此解答即可。
【详解】(1)60÷1=60(千米/时)
120÷2=60(千米/时)
5×60=300(千米)
6×60=360(千米)
如表所示:
时间(时) 1 2 3 4 5 6
路程(千米) 60 120 180 240 300 360
(2)因为路程÷时间=速度(一定),所以这辆汽车行驶的路程和所需的时间的比值一定,则这辆汽车行驶的路程和所需的时间成正比例。
(3)如图所示:
发现:这辆汽车行驶的路程和所需的时间形成的图像是一条直线。
(4)因为540÷9=60,所以点(9,540)在这条直线上,这一点表示汽车9小时行驶了540千米。
【点睛】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
19.(1)(2)(3)见详解
【分析】(1)写出时间和路程的比,并求出比值,然后比较比值的大小;根据数量关系判断比值表示的意义;
(2)判断表格中的两个量的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例;
(3)估计表格中的数据,在横轴表示时间,竖轴表示路程的图中先描出对应的点,然后画出图像即可。
【详解】(1)80∶1=80
160∶2=80
240∶3=80
320∶4=80
400∶5=80
480∶6=80
比值都是80,比值相等,所以比值表示速度;
(2)速度=路程÷时间,速度一定,所以汽车行驶的路程与时间成正比例关系;
(3)由图可知,一个小格代表40千米,那么200千米的时候对应的时间点就是2小时和3小时之间的2.5小时。
【点睛】本题重点考查学生由表格获取信息能力及利用描点法画图能力,难点为正比例关系的判断。
20.(1)北;西;900
(2)图见详解
【分析】(1)先计算出公园到广场的实际距离,再根据地图上方向的规定:上北下南,左西右东;以公园为观察点,说出广场的位置;
(2)根据实际距离和图上距离的换算,以公园为观察点,画出喷水池的位置。
【详解】(1)经过测量,公园到广场的图上距离是3厘米;
3÷
=3×30000
=90000(厘米)
90000厘米=900米
广场在公园北偏西30°方向上,实际距离是900米。
(2)作图如下:
750米=75000厘米
75000×=2.5(厘米)
【点睛】本题考查根据方向,角度和距离确定物体位置,以及实际距离与图上距离的换算。
21.(1)(1,11);(3,8);
(2)(3)图形见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此填空即可;
(2)把三角形ABC绕点B顺时针旋转90°后,点B的位置不动,其余各部分均绕点B按相同方向旋转相同的度数即可;
(3)将图中的三角形的各边长都扩大到原来的3倍即可。
【详解】(1)用数对表示A,C两点的位置:A(1,11),C(3,8)。
(2)(3)如图所示:
【点睛】本题考查图形的放大或缩小,明确放大的是图形的各个边长是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
必考小专题:比例综合-数学六年级下册北师大版
1.酸梅汤是夏季防暑去火的上佳饮品。林阿姨多次尝试,发现用60毫升的酸梅原汁和140毫升的水配制的酸梅汤口感最佳。现在林阿姨打算配制3600毫升同样口感的酸梅汤,需要酸梅原汁多少毫升?
2.在一幅比例尺是1∶6000000的地图上,量得甲、乙两地之间的距离大约是7厘米,一辆客车和一辆货车同时从甲、乙两地出发,相向而行,3小时相遇,已知客车和货车的速度比是4∶3,客车、货车的速度各是多少?
3.A地到C地的高速公路经过B地,全程距离大约为440千米,A地到B地大约为120千米。一辆汽车从A地出发开往C地,当行驶到B地时用了1.5小时。按照这个速度,A地到C地全程需要多少小时?(用比例解题)
4.科学家往往具有非凡的毅力和不懈探索的精神,居里夫人从24吨废矿渣里才提炼出0.1克镭。照这样计算,要提炼1.5克镭,需要多少吨这样的废矿渣?(用比例解答)
5.甲、乙两地之间的高速铁路大约长1600千米。丙地在甲地、乙地之间甲地到丙地的高速铁路大约长700千米。一列由甲地开往乙地的高铁列车9:00出发,11:30到达丙地。按照这样的平均速度,6小时能从甲地到乙地吗?
6.为创建全国文明城市,阳城公园种了一块三角形的草坪,在比例尺1∶8000的平面图上量得这块草坪的底是2.5厘米,高是0.4厘米。这块三角形草地的实际面积是多少?
7.李老师家装修新房,计划用边长是0.8米的正方形瓷砖铺客厅地面,这样需要40块;后来改为面积是0.8平方米的正方形瓷砖铺地,需要多少块?(列比例解答)
8.电动车厂原计划每天生产电动车400辆,25天可以完成任务,实际每天生产500辆,实际多少天可以完成任务?(用比例解)
9.李师傅计划加工一批零件,前五天加工了120个,照这样计算,再用18天就可以做完,这批零件一共有多少个?(用比例解)
10.一列火车从甲地开往乙地,9小时行驶720千米。照这样的速度,行驶完全程960km,一共需要多少小时?(用比例解)
11.博物馆展出一个高为18.2厘米的秦代将军俑模型,它的高度与实际高度的比是1∶10。这个将军俑的实际高度是多少厘米?
12.小丽在太阳下某一位置测得自己的影长是1.2米,在同一时间同一地点把20分米长的竹竿立在地上,测得竹竿的影长是15分米,小丽的身高是多少米?(用比例解)
13.小明家在A市,小强家在C市,小明和爸爸从A市乘火车途经B市去C市找小强,全程共行驶多少千米?(测量结果取整厘米数)
14.(1)按1∶2画出平行四边形缩小后的图形。
(2)有一块长方形池塘长200米、宽120米,用的比例尺在上面的格子图中画出这个长方形池塘的平面图,每个方格边长是1厘米。(先计算,再画图)
15.在一幅比例尺为1∶2000000的地图上,量得甲乙两地之间的公路长10厘米。一辆汽车和一辆货车从两地同时出发相向而行,汽车以每时58千米的速度行驶,2小时后在超过中点16千米的地方相遇。货车每时行多少千米?
16.新星小学的校园是一个长600米,宽400米的长方形。
(1)如果让你画出新星小学的校园平面图,你选择的比例尺是:( )∶( )。
(2)分别求出长和宽的图上距离,并在下面图中画出校园平面图。
长的图上距离:
宽的图上距离:
平面图:
17.淘气和同学们去劳动基地摘了一筐草莓,计划将草莓分装在小袋子里送给敬老院。淘气设计的方案如下:
方案 ① ② ③ ④
每袋草莓的质量/千克 0.4 0.5 0.8 1.25
草莓的袋数 250 200 125 80
(1)每袋草莓的质量与草莓的袋数有什么关系,请说明理由。
(2)如果每袋草莓的质量是2.5千克,可分成多少袋?
(3)你喜欢哪种方案?说说理由。
18.一辆汽车的行驶的路程和所需的时间如下表。
时间(时) 1 2 3 4 5 6
路程(千米) 60 120 180 240
(1)把上表填写完整。
(2)这辆汽车行驶的路程和所需的时间是否成正比例,请说明理由。
(3)根据上表描点,再顺次连接各点,你发现了什么?
(4)点(9,540)在这条直线上吗?这一点表示什么含意?
19.一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/千米 80 160 240 320 400 480
(1)写出几组路程与相对应的时间的比,并比较比值的大小。说一说这个比值表示什么。
(2)汽车行驶的路程与时间成正比例关系还是反比例关系?为什么?
(3)在图中描出表示路程和相对应时间的点,然后把它们按顺序连起来。并估计一下行200千米大约需要多少时间。
20.下面是公园街区的平面示意图。
(1)广场在公园( )偏( )30°方向上,实际距离是( )米。
(2)喷水池在广场西南方向750米处,请在图上画出位置用点标明。
21.填一填,画一画。
(1)用数对表示A,C两点的位置:A( ),C( )。
(2)画出图中的三角形ABC绕B点顺时针旋转90°后的图形。
(3)画出图中的三角形ABC按3∶1放大后的图形。
参考答案:
1.1080毫升
【分析】由信息“60毫升的酸梅原汁和140毫升的水配制酸梅汤,口感最佳”可知,酸梅与水的比是一定的,根据此列出方程解答。设需要酸梅x毫升,那么水就有(3600-x)毫升,根据酸梅:水的比一定列出比例:x∶(3600-x)=60∶140,解比例即可。
【详解】解:设需要酸梅x毫升,那么水就有(3600-x)毫升。
x∶(3600-x)=60∶140
140x=60×(3600-x)
140x=216000-60x
140x+60x=21600
200x=216000
x=216000÷200
x=1080
答:需要酸梅原汁毫升1080毫升。
【点睛】解答此题关键找出酸梅的浓度不变,据此设出未知数,找出相关的量,列比例解答即可。
2.客车80千米/时,货车60千米/时
【分析】根据实际距离=图上距离÷比例尺,据此求出甲、乙两地的实际距离,再根据相遇问题中,相遇路程÷相遇时间=速度和,据此求出客车和货车的速度和,再根据按比分配问题求出客车、货车的速度即可。
【详解】7÷=42000000(厘米)=420(千米)
420÷3×
=140×
=80(千米/时)
420÷3×
=140×
=60(千米/时)
答:客车的速度是80千米/时,货车的速度是60千米/时。
【点睛】本题考查比例尺,明确图上距离、实际距离和比例尺之间的关系是解题的关键。
3.5.5小时
【分析】由题意可知,汽车的速度不变,则路程和时间成正比例关系,路程÷时间=速度(一定),把行完全程需要的时间设为未知数,A地到C地的路程∶A地到C地的时间=A地到B地的路程∶A地到B地的时间,据此解答。
【详解】解:设A地到C地全程需要x小时。
440∶x=120∶1.5
120x=440×1.5
120x=660
x=660÷120
x=5.5
答:A地到C地全程需要5.5小时。
【点睛】本题主要考查应用比例解决实际问题,理解速度一定时,路程与时间成正比例是解答题目的关键。
4.360吨
【分析】由题意可知,提炼每克镭需要废矿渣的质量不变,则需要废矿渣的质量和镭的质量成正比例关系,需要废矿渣的质量∶提炼镭的质量=24∶0.1,据此列方程解答。
【详解】解:设需要吨这样的废矿渣。
答:需要360吨这样的废矿渣。
【点睛】本题主要考查比例的应用,明确两种相关联的量成正比例关系是解答题目的关键。
5.能
【分析】根据题意可知,甲地到丙地需要2.5小时,根据速度=路程÷时间,速度一定,则路程和时间成正比例,假设甲地到乙地需要x小时,列方程为1600∶x=700∶2.5,然后解出方程,最后和6小时比较即可。
【详解】11:30-9:00=2小时30分钟
2小时30分钟=2.5小时
解:设甲地到乙地需要x小时。
1600∶x=700∶2.5
700x=1600×2.5
700x=4000
x=4000÷700
x=
<6
答:6小时能从甲地到乙地。
【点睛】本题主要考查了正比例的应用,找到相应的数量关系式是解答本题的关键。
6.3200平方米
【分析】根据实际距离=图上距离÷比例尺,据此求出这块草坪的底和高的实际长度,再根据三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】2.5÷=20000(厘米)=200(米)
0.4÷=3200(厘米)=32(米)
200×32÷2
=6400÷2
=3200(平方米)
答:这块三角形草地的实际面积是3200平方米。
【点睛】本题考查比例尺,结合三角形的面积的计算方法是解题的关键。
7.32块
【分析】根据题意可知,每块正方形瓷砖的面积×块数=客厅地面的面积(一定),积一定,那么每块正方形瓷砖的面积与块数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设需要块。
0.8=0.8×0.8×40
0.8=25.6
=25.6÷0.8
=32
答:需要32块。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
8.20天
【分析】设实际x天可以完成任务,根据每天生产数量×天数=总数量(一定),列出反比例算式解答即可。
【详解】解:设实际x天可以完成任务。
500x=400×25
500x=10000
500x÷500=10000÷500
x=20
答:实际20天可以完成任务。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
9.552个
【分析】根据题意知道,工作效率一定,工作量和工作时间成正比例,由此列式解答即可。
【详解】解:设这批零件一共有x个,则:
x∶(5+18)=120∶5
x∶23=120∶5
5x=120×23
5x=2760
5x÷5=2760÷5
x=552
答:这批零件一共有552个。
【点睛】解答此题的关键是判断哪两种量成何比例,然后找准对应量,列式解答即可。
10.12小时
【分析】这个题目中速度是一定的,路程÷时间=速度。
【详解】解:设一共需要小时
960∶=720∶9
720=960×9
=12
答:一共需要12小时。
【点睛】能够知道题目中哪个量是不变的,知道已知两个量的关系是正比例关系还是反比例关系。
11.182厘米
【分析】根据题意可知,秦代将军俑模型的高度∶实际高度=1∶10,比值一定,秦代将军俑模型的高度和实际高度成正比例,设这个将军俑的实际高度是x厘米,列方程为18.2∶x=1∶10,然后解出方程即可。
【详解】解:设这个将军俑的实际高度是x厘米。
18.2∶x=1∶10
x=18.2×10
x=182
答:这个将军俑的实际高度是182厘米。
【点睛】本题考查了正比例的认识和应用,可列方程解决问题。
12.1.6米
【分析】同一时间同一地点,竿高和影长成正比例,即,据此等量关系列出比例解答即可。
【详解】20分米=2米
15分米=1.5米
解:设小丽的身高是x米。
x∶1.2=2∶1.5
1.5x=1.2×2
1.5x=2.4
x=2.4÷1.5
x=1.6
答:小丽的身高是1.6米。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
13.1500千米
【分析】先量出从A市途经B市到C市的图上距离,再根据“图上距离÷比例尺=实际距离”解答即可。
【详解】(1+2)÷
=3÷
=3×50000000
=150000000(厘米)
150000000厘米=1500千米
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
14.(1)见详解;
(2)长5厘米;宽3厘米;图形见详解
【分析】(1)原来平行四边形的底边为8厘米,缩小后对应的底边为8×=4(厘米),原来平行四边形的高为4厘米,缩小后对应的高为4×=2(厘米),平行四边形缩小以后形状不变,只是位置和大小发生了变化;
(2)根据“图上距离=实际距离×比例尺”分别计算出这个长方形池塘在格子图中的长和宽,再根据计算结果画出长方形池塘的平面图,据此解答。
【详解】(1)分析可知:
(2)200米=20000厘米
120米=12000厘米
长:20000×=5(厘米)
宽:12000×=3(厘米)
作图如下:
【点睛】掌握缩小图形的作图方法以及图上距离和实际距离换算的方法是解答题目的关键。
15.42千米
【分析】根据“实际距离=图上距离÷比例尺”求出甲乙两地之间的实际距离,再利用速度和=总路程÷相遇时间求出汽车和货车的速度和,最后用减法求出货车的速度,据此解答。
【详解】10÷=20000000(厘米)
20000000厘米=200千米
200÷2-58
=100-58
=42(千米)
答:货车每时行42千米。
【点睛】本题考查比例尺,求出甲乙两地的实际距离是解题的关键。
16.(1)1∶20000
(2)见详解
【分析】(1)图上距离∶实际距离=比例尺,据此确定比例尺;
(2)图上距离=实际距离×比例尺,据此求出图上距离,作图即可。
【详解】(1)选择的比例尺是:1∶20000。
(2)600米=60000厘米
400米=40000厘米
长的图上距离:60000×=3(厘米)
宽的图上距离:40000×=2(厘米)
(答案不唯一)
【点睛】关键是理解比例尺的意义,掌握图上距离与实际距离的换算方法。
17.(1)反比例,因为每袋草莓的质量与草莓的袋数的乘积一定;(2)40袋;(3)第④个,因为袋数比较少,同学们比较好拿
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。观察表格可知,每袋草莓的质量和草莓的袋数的乘积一定,所以它们成反比例;
(2)根据每袋草莓的质量×草莓的袋数=总质量,用总质量除以2.5千克,即可求出草莓的袋数;
(3)给出的理由合理即可。
【详解】(1)0.4×250=100(千克)
0.5×200=100(千克)
0.8×125=100(千克)
1.25×80=100(千克)
每袋草莓的质量和草莓的袋数的乘积一定,所以它们成反比例。
(2)100÷2.5=40(袋)
答:如果每袋草莓的质量是2.5千克,可分成40袋。
(3)我喜欢第④个方案,因为袋数比较少,同学们比较好拿。(答案不唯一)
【点睛】本题主要考查了反比例的意义和辨识。
18.(1)见详解
(2)成正比例,理由见详解
(3)这辆汽车行驶的路程和所需的时间形成的图像是一条直线
(4)在,这一点表示汽车9小时行驶了540千米
【分析】(1)根据路程÷时间=速度,60÷1=60,120÷2=60,据此发现汽车的速度是一定的,再根据速度×时间=路程,据此计算并填空即可;
(2)两个相关联的量,若它们的比值一定,则它们成正比例;若它们的乘积一定,则它们成反比例;
(3)根据统计表上的数据在统计图上描出各点,再顺次连接各点,最后再观察即可;
(4)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,也就是横轴表示时间,纵轴表示路程,据此解答即可。
【详解】(1)60÷1=60(千米/时)
120÷2=60(千米/时)
5×60=300(千米)
6×60=360(千米)
如表所示:
时间(时) 1 2 3 4 5 6
路程(千米) 60 120 180 240 300 360
(2)因为路程÷时间=速度(一定),所以这辆汽车行驶的路程和所需的时间的比值一定,则这辆汽车行驶的路程和所需的时间成正比例。
(3)如图所示:
发现:这辆汽车行驶的路程和所需的时间形成的图像是一条直线。
(4)因为540÷9=60,所以点(9,540)在这条直线上,这一点表示汽车9小时行驶了540千米。
【点睛】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
19.(1)(2)(3)见详解
【分析】(1)写出时间和路程的比,并求出比值,然后比较比值的大小;根据数量关系判断比值表示的意义;
(2)判断表格中的两个量的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例;
(3)估计表格中的数据,在横轴表示时间,竖轴表示路程的图中先描出对应的点,然后画出图像即可。
【详解】(1)80∶1=80
160∶2=80
240∶3=80
320∶4=80
400∶5=80
480∶6=80
比值都是80,比值相等,所以比值表示速度;
(2)速度=路程÷时间,速度一定,所以汽车行驶的路程与时间成正比例关系;
(3)由图可知,一个小格代表40千米,那么200千米的时候对应的时间点就是2小时和3小时之间的2.5小时。
【点睛】本题重点考查学生由表格获取信息能力及利用描点法画图能力,难点为正比例关系的判断。
20.(1)北;西;900
(2)图见详解
【分析】(1)先计算出公园到广场的实际距离,再根据地图上方向的规定:上北下南,左西右东;以公园为观察点,说出广场的位置;
(2)根据实际距离和图上距离的换算,以公园为观察点,画出喷水池的位置。
【详解】(1)经过测量,公园到广场的图上距离是3厘米;
3÷
=3×30000
=90000(厘米)
90000厘米=900米
广场在公园北偏西30°方向上,实际距离是900米。
(2)作图如下:
750米=75000厘米
75000×=2.5(厘米)
【点睛】本题考查根据方向,角度和距离确定物体位置,以及实际距离与图上距离的换算。
21.(1)(1,11);(3,8);
(2)(3)图形见详解
【分析】(1)根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此填空即可;
(2)把三角形ABC绕点B顺时针旋转90°后,点B的位置不动,其余各部分均绕点B按相同方向旋转相同的度数即可;
(3)将图中的三角形的各边长都扩大到原来的3倍即可。
【详解】(1)用数对表示A,C两点的位置:A(1,11),C(3,8)。
(2)(3)如图所示:
【点睛】本题考查图形的放大或缩小,明确放大的是图形的各个边长是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
