必考小专题:比例综合-数学六年级下册人教版(含答案)
文档属性
| 名称 | 必考小专题:比例综合-数学六年级下册人教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 811.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
必考小专题:比例综合-数学六年级下册人教版
1.陈浩家距离外婆家大约有460千米,汽车每100千米耗油8升,按这个耗油量,出发时加满40升汽油,能到外婆家吗?(用比例知识解答)
2.一辆运货汽车从甲地到乙地,平均每小时行驶72千米,10小时到达。回去时空车原路返回,每小时可以比来的时候多行18千米,多长时间能够返回甲地?(用比例解)
3.用18克糖和270克水配制成一杯糖水,如果保持糖水一样甜,加入150克水后需加入多少克糖?
4.开车从安阳到北京要行驶约500千米。一辆汽车从安阳出发前往北京,5小时行了全程的。照这样的速度,到达北京共需要多少小时?
5.在一幅比例尺是的地图上,量得A、B两座城市之间的距离是15cm。一辆客车和一辆小轿车同时从两地相向而行,3小时相遇。已知客车和小轿车的速度比是,这两辆车的速度各是多少?
6.亮亮家造了新房,准备用边长是0.4米的正方形地砖装饰客厅地面,这样需要180块,装修师傅建议改用边长0.6米的正方形地砖铺地。请你算一算需要多少块?(请用比例解答)
7.小林和小华共读一本文学名著,小林每天读20页,6天读完。小华每天读30页,几天可以读完?(用比例解)
(1)分析:每天读的页数和天数成( )比例关系。
(2)请你用比例方法来解答。
8.学校要栽一批树,每班栽20棵,要12个班才能完成任务,如果每班栽30棵,需要几个班可以完成?(用比例解决问题)
9.如图,科学课上,老师在简易杠杆的两边分别放上A、B两个物体。已知A物体重120克,且杠杆保持平衡,那么B物体重多少克?(用比例解答)
10.绍兴地铁1号线全长47.1千米,画在一幅比例尺为1∶150000的地图上,它的图上距离是多少厘米?
11.风能作为一种清洁的可再生能源,越来越受到世界各国的重视。我国风能资源丰富,它取之不尽,用之不竭。某校数学实践小组到石城县八卦脑风景区实践,测得一座风力发电架在阳光下的影长是64米。同时把一根长2米的测杆直立在地上,测得在阳光下的影长是1.6米。风力发电架的高是多少米?(用比例解决问题)
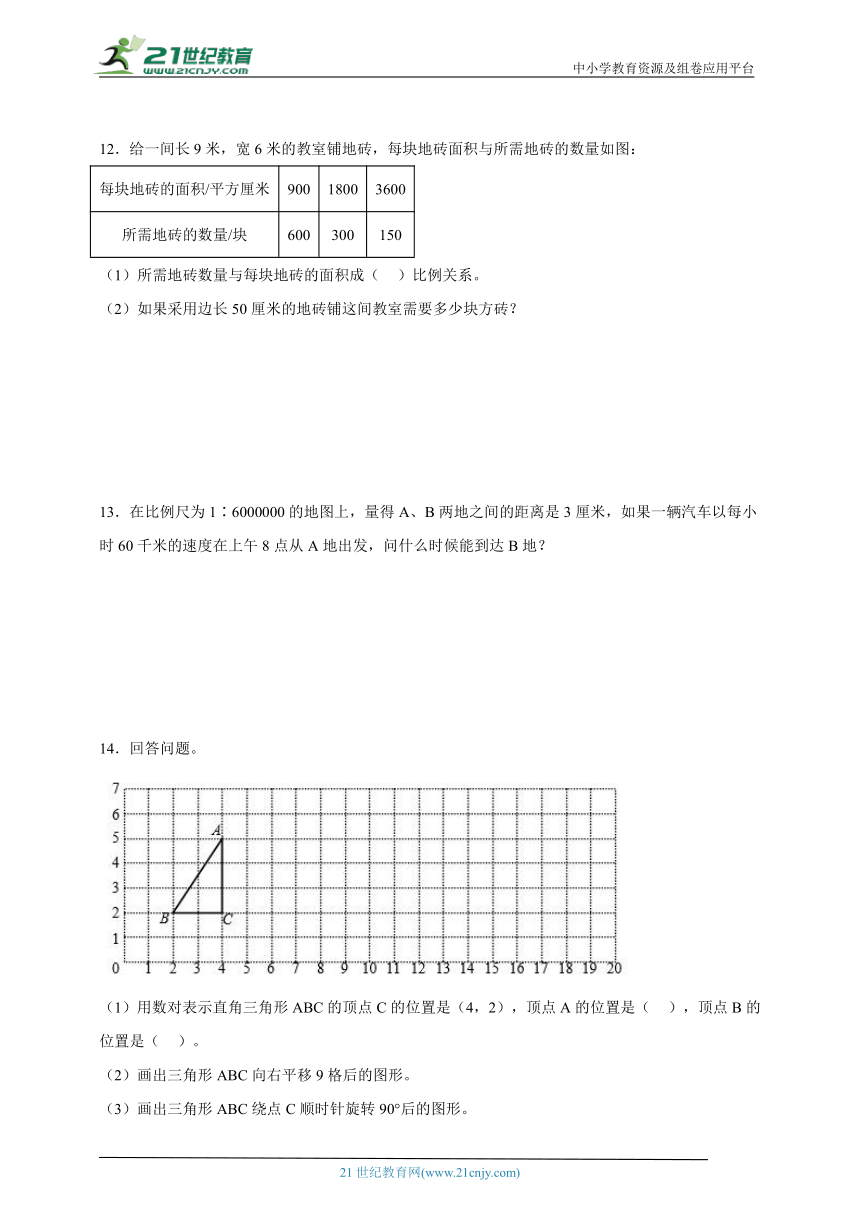
12.给一间长9米,宽6米的教室铺地砖,每块地砖面积与所需地砖的数量如图:
每块地砖的面积/平方厘米 900 1800 3600
所需地砖的数量/块 600 300 150
(1)所需地砖数量与每块地砖的面积成( )比例关系。
(2)如果采用边长50厘米的地砖铺这间教室需要多少块方砖?
13.在比例尺为1∶6000000的地图上,量得A、B两地之间的距离是3厘米,如果一辆汽车以每小时60千米的速度在上午8点从A地出发,问什么时候能到达B地?
14.回答问题。
(1)用数对表示直角三角形ABC的顶点C的位置是(4,2),顶点A的位置是( ),顶点B的位置是( )。
(2)画出三角形ABC向右平移9格后的图形。
(3)画出三角形ABC绕点C顺时针旋转90°后的图形。
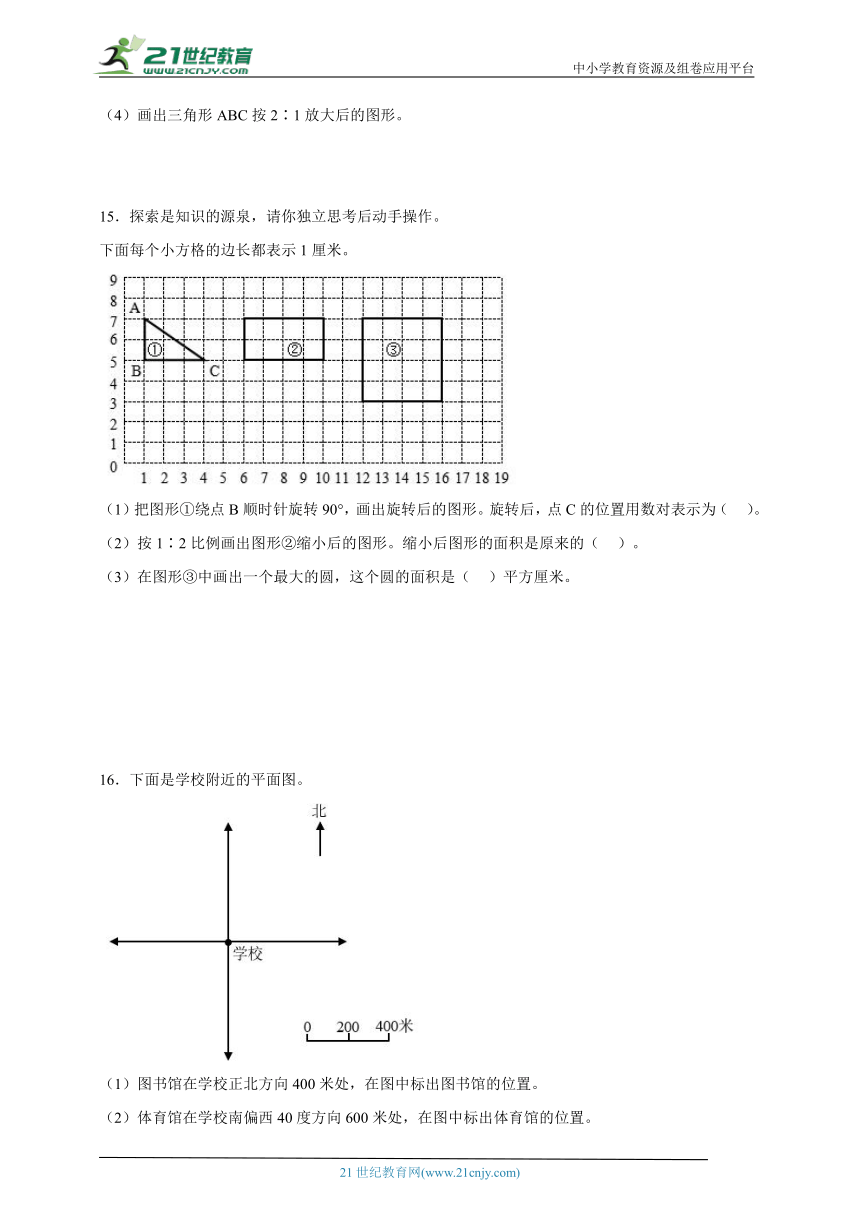
(4)画出三角形ABC按2∶1放大后的图形。
15.探索是知识的源泉,请你独立思考后动手操作。
下面每个小方格的边长都表示1厘米。
(1)把图形①绕点B顺时针旋转90°,画出旋转后的图形。旋转后,点C的位置用数对表示为( )。
(2)按1∶2比例画出图形②缩小后的图形。缩小后图形的面积是原来的( )。
(3)在图形③中画出一个最大的圆,这个圆的面积是( )平方厘米。
16.下面是学校附近的平面图。
(1)图书馆在学校正北方向400米处,在图中标出图书馆的位置。
(2)体育馆在学校南偏西40度方向600米处,在图中标出体育馆的位置。
(3)小丽从体育馆向( )偏( )( )度方向走( )米就到学校。
17.化肥厂生产一批化肥,每天生产30吨,50天完成。如果要40天完成任务,每天应多生产多少吨?(用比例解)
18.西安钟楼是中国现存钟楼中形制最大、保存最完整的一座钟楼,总高36米。某展馆设计制作了钟楼的模型,模型的高度与实际高度的比是1∶50。模型的高度是多少米?(用比例解)
19.张同周末去爬山,上山时每小时大约走3.5千米,用了2.4小时,下山时按原路返回,比上山少用了0.3小时,他下山时每小时走多少千米?(用比例解)
20.把1.5米长的竹竿直立在地上,量得它的影长1.2米,同时量得一棵大树的影长3.6米,这棵大树高多少米?(用比例解)
21.下图表示小兔和小羊的奔跑情况。
(1)它们奔跑的路程和所需的时间成( )比例。
(2)根据图象计算小兔18分跑了多少千米?小羊18分跑了多少千米?(用比例解决)
22.在比例尺是1∶2000000的地图上,量的甲乙两地的距离是3.6厘米。如果汽车以每小时30千米的速度于上午8时整从甲地开出,走完这段路程,到达乙地时是什么时间?
参考答案:
1.能
【分析】根据题意可知,汽油的总升数÷行驶的千米数=每千米消耗汽油的升数(一定),则汽油的总升数和行驶的千米数的比值一定,它们成正比例关系,据此设到外婆家需要x升汽油,列比例为x∶460=8∶100,然后解出比例即可。
【详解】解:设到外婆家需要x升汽油。
x∶460=8∶100
100x=8×460
100x=3680
x=3680÷100
x=36.8
36.8<40
40升汽油够用。
答:出发时加满40升汽油,能到外婆家。
【点睛】本题主要考查了正比例的应用,判断相关量是正比例还是反比例是解答本题的关键。
2.8小时
【分析】根据题意可知,汽车的速度×行驶时间=路程(一定),汽车的速度和行驶时间成反比例,据此设x小时能够返回甲地,列比例为(72+18)×x=72×10,然后解出比例即可。
【详解】解:设x小时能够返回甲地。
(72+18)×x=72×10
90x=72×10
90x=720
x=720÷90
x=8
答:8小时能够返回甲地。
【点睛】本题主要考查了反比例的应用,判断相关量是正比例还是反比例是解答本题的关键。
3.10克
【分析】根据题意可知,要保持糖水一样甜,则加入的糖水质量比和原来的质量比一样,据此设加入150克水后需加入x克糖,列比例为150∶x=270∶18,然后解出比例即可。
【详解】解:加入150克水后需加入x克糖。
150∶x=270∶18
270x=150×18
270x=2700
x=2700÷270
x=10
答:加入150克水后需加入10克糖。
【点睛】本题考查了用比例解决问题,掌握解比例的方法是解答本题的关键。
4.6.25小时
【分析】把全长看作单位“1”,根据分数乘法的意义,用500×即可求出5小时行驶的路程,根据路程÷时间=速度,速度一定,路程和时间成正比例,设到达北京共需要x小时,列比例为:500∶x=(500×)∶5,然后解出比例即可。
【详解】解:设到达北京共需要x小时。
500∶x=(500×)∶5
500∶x=400∶5
400x=500×5
400x=2500
x=2500÷400
x=6.25
答:到达北京共需要6.25小时。
【点睛】本题主要考查了正比例的应用,掌握解比例的方法是解答本题的关键。
5.千米/小时;千米/小时
【分析】实际距离=图上距离÷比例尺,依据公式求出实际距离,用实际距离除以时间求出客车和小轿车的速度和,再按比例分配求出他们的速度。
【详解】15÷
=15×3000000
=(厘米)
=450(千米)
(千米/小时)
150÷(2+3)×2
=30×2
=60(千米/小时)
150÷(2+3)×3
=30×3
=90(千米/小时)
答:客车的速度是千米/小时,小轿车的速度是千米/小时。
【点睛】此题考查比例尺的应用,明确实际距离与图上距离的换算方法是解题的关键。
6.80块
【分析】因为每块地砖的面积×地砖的块数=客厅地面的面积(一定),所以每块地砖的面积和地砖的块数成反比例。也就是边长0.4米的地砖的面积×边长0.4米的地砖的块数=边长0.6米的地砖的面积×边长0.6米的地砖的块数,可以根据这个等量关系列比例解答。
【详解】解:设需要x块。
0.6×0.6×x=0.4×0.4×180
0.36x=0.16×180
0.36x=28.8
0.36x÷0.36=28.8÷0.36
x=80
答:需要80块。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
7.(1)反;(2)4天
【分析】(1)根据xy=k(一定),x和y成反比例关系,确定比例关系;
(2)设x天可以读完,根据每天读的页数×读的天数=总页数(一定),列出反比例算式解答即可。
【详解】(1)每天读的页数×读的天数=总页数(一定),每天读的页数和天数成反比例关系。
(2)解:设x天可以读完。
30x=20×6
30x=120
30x÷30=120÷30
x=4
答:4天可以读完。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
8.8个
【分析】由题意可知,这批树的总棵数不变,每班栽树的棵数×需要的班数=这批树的总棵数(一定),则每班栽树的棵数和需要的班数成反比例,据此列出比例并解比例求出未知数的值。
【详解】解:设需要x个班可以完成。
30×x=20×12
30x=240
x=240÷30
x=8
答:需要8个班可以完成。
【点睛】本题主要考查反比例的应用,明确题目中相关联的两种量成反比例关系是解答题目的关键。
9.160克
【分析】根据平衡原理,力臂的长度与所挂重物的质量的乘积一定,所以它们成反比例关系,据此设B物体重x克,列比例为3x=120×4,然后解比例即可。
【详解】解:设B物体重x克。
3x=120×4
3x=480
x=480÷3
x=160
答:B物体重160克。
【点睛】本题考查了反比例的应用,解答本题的关键是理解力臂的长度与所挂重物的质量的乘积是一定的。
10.31.4厘米
【分析】已知比例尺和实际距离,求图上距离,可根据“图上距离=实际距离×比例尺”直接列式计算。
【详解】47.1千米=4710000厘米
4710000×=31.4(厘米)
答:它的图上距离是31.4厘米。
【点睛】图上距离一般用厘米作单位,实际距离一般用米或千米作单位,求图上距离时可先把实际距离换算成以厘米为单位的。
11.80米
【分析】根据实际长与影长的比值不变的关系,列出比例方程进行解答即可。
【详解】解:设风力发电架的高是x米。
答:风力发电架的高是80米。
【点睛】本题考查用比例解决问题,解答本题的关键是掌握题中的数量关系。
12.(1)反;
(2)216块
【分析】(1)判断两种量成正比例还是成反比例,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。
(2)每块地砖的面积×所需地砖的块数=这间教室地面的面积(一定),所以所需地砖数量与每块地砖的面积成反比例关系。也就是900×600和边长50厘米的地砖的面积×边长50厘米的地砖的块数相等,可以根据这个数量关系列比例解答。
【详解】(1)900×600=1800×300=3600×150=540000,也就是每块地砖的面积×所需地砖的块数=540000(一定),即每块地砖的面积与所需地砖的块数的乘积一定,所以所需地砖数量与每块地砖的面积成反比例关系。
(2)解:设采用边长50厘米的地砖铺这间教室需要x块方砖,
50×50×x=900×600
2500x=540000
2500x÷2500=540000÷2500
x=216
答:如果采用边长50厘米的地砖铺这间教室需要216块方砖。
【点睛】此题主要考查了反比例的意义及反比例的应用。用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
13.11时
【分析】根据实际距离=图上距离÷比例尺,据此求出A、B两地之间的实际距离,再根据路程÷速度=时间,据此求出汽车行驶的时间,最后用8加上行驶的时间即可求解。
【详解】3÷=3×6000000=18000000(厘米)
18000000厘米=180千米
180÷60=3(小时)
8+3=11(时)
答:11时能到达B地。
【点睛】本题考查路程问题,明确比例尺、图上距离和实际距离之间的关系是解题的关键。
14.(1)(4,5);(2,2)
(2)(3)(4)见详解
【分析】(1)用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
(2)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
(3)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(4)把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1。
【详解】(1)顶点A的位置是(4,5),顶点B的位置是(2,2)。
(2)(3)(4)
【点睛】关键是掌握用数对表示位置的方法,会作平移和旋转后的图形,图形放大或缩小是指对应边放大或缩小。
15.(1)图见详解;(1,2);(2)图见详解;;(3)图见详解;12.56
【分析】(1)根据图形旋转的特征对图形①进行位置变化。结合数对确定位置的方法:先看在第几列,这个数就是数对中的第一个数,再看在第几行,这个数就是数对中的第二个数,据此确定C点的位置;(2)按1∶2的比例缩小图形②就是将原来图形的长和宽都缩小为原来的,原来的长是4,缩小后的长是2,原来的宽是2,缩小后的宽是1,再根据长方形的面积公式,分别计算出原来长方形的面积和现在长方形的面积,即可解答;(3)要在正方形里面画一个最大的圆,这个圆的直径应该和正方形的边长相等,再根据圆的面积公式,求出圆的面积即可。
【详解】(1)图形①绕点B顺时针旋转90°,B点保持不变,C点旋转到(1,2)处,A点旋转到(3,5)处,见下图:
点C的位置用数对表示为(1,2)。
(2)如下图:
缩小后的长方形面积:1×2=2(平方厘米)
原来的长方形面积:4×2=8(平方厘米)
所以缩小后图形的面积是原来的。
(3)如下图:
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
所以这个圆的面积是12.56平方厘米。
【点睛】本题考查的知识点比较多,解答的关键是熟练掌握作图的特征、数对的写法、长方形的面积公式以及圆的面积公式。
16.(1)、(2)见详解
(3)东;北;50;600
【分析】根据平面图上的方向,上北下南,左西右东,及题中给出的线段比例尺,以学校的位置为观测点,即可标出图书馆及体育馆位置;
以体育馆为观测点,确定学校在体育馆的方向、角度和距离即可确定小丽怎么从体育馆到学校的行走路线。
【详解】(1)400÷200=2(厘米)
(2)600÷200=3(厘米)
图书馆、体育馆位置如下:
(3)以体育馆为观测点,小丽从体育馆向(东)偏(北)(50)度或(北)偏(东)(40)度方向走(600)米就到学校。
【点睛】此题考查了利用方向、角度与距离在平面图中确定物体位置的方法以及线段比例尺的灵活应用。
17.7.5吨
【分析】根据题意知道总工作量一定,工作时间和工作效率成反比例,由此列式解答即可。
【详解】解:设每天应多生产x吨,可得:
40×(30+x)=30×50
1200+40x=1500
1200+40x-1200=1500-1200
40x=300
40x÷40=300÷40
x=7.5
答:每天应多生产7.5吨。
【点睛】解答此题的关键是,弄清题意,根据工作效率、工作时间和工作量之间的关系,先判断哪两种量成何比例,再找准对应量,列式解答即可。
18.0.72米
【分析】根据题意可知,钟楼模型的高度∶钟楼实际的高度=1∶50,据此列出比例方程,并求解。
【详解】解:设模型的高度是米。
∶36=1∶50
50=36×1
=36÷50
=0.72
答:模型的高度是0.72米。
【点睛】本题考查比例的应用,从题目中找到等量关系,根据等量关系列出方程。
19.4千米
【分析】设下山时每小时走x千米。当路程一定时,速度与时间成反比例关系,即上山的速度×上山的时间=下山的速度×下山的时间。根据这个数量关系可有(2.4-0.3)x=3.5×2.4。
【详解】解:设他下山时每小时走x千米。
(2.4-0.3)x=3.5×2.4
2.1x=8.4
x=8.4÷2.1
x=4
答:他下山时每小时走4千米。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
20.4.5米
【分析】竹竿的实际长度和影子长的比,和大树的实际长度和影子长的比是相等的,据此列比例解比例即可。
【详解】解:设这棵大树高x米。
1.5∶1.2=x∶3.6
1.2x=1.5×3.6
1.2x=5.4
1.2x÷1.2=5.4÷1.2
x=4.5
答:这棵大树高4.5米。
【点睛】本题考查了比例的应用,能正确理解题意并列比例是解题的关键。
21.(1)正;(2)21.6千米; 14.4千米
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。根据速度=路程÷时间,观察统计图可知,它们的速度一定,所以它们奔跑的路程和所需的时间成正比例。
(2)设小兔18分跑了x千米,列方程为24∶20=x∶18,然后解出方程即可;设小羊18分跑了y千米,列方程为20∶25=y∶18,然后解出方程即可。
【详解】(1)观察统计图可知,两条线都是直线,所以小兔和小羊的速度一定,则它们奔跑的路程和所需的时间成正比例。
(2)解:设小兔18分跑了x千米。
24∶20=x∶18
20x=24×18
20x=432
x=432÷20
x=21.6
解:设小羊18分跑了y千米。
20∶25=y∶18
25y=20×18
25y=360
y=360÷25
y=14.4
答:小兔18分跑了21.6千米;小羊18分跑了14.4千米。
【点睛】本题考查了正比例的辨识和应用,明确相关联的量是正比例还是反比例是解答本题的关键。
22.10时24分
【分析】根据实际距离=图上距离÷比例尺,据此求出甲乙两地的实际距离,再根据路程÷速度=时间,求出走完这段路需要多长时间,再用8加上走完这段路需要的时间即可求出到达乙地时是什么时间。
【详解】3.6÷=3.6×2000000=7200000(厘米)
7200000厘米=72千米
72÷30=2.4(时)=2时24分
8时+2时24分=10时24分
答:走完这段路程,到达乙地时是10时24分。
【点睛】本题考查路程问题,明确图上距离、实际距离和比例尺之间的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
必考小专题:比例综合-数学六年级下册人教版
1.陈浩家距离外婆家大约有460千米,汽车每100千米耗油8升,按这个耗油量,出发时加满40升汽油,能到外婆家吗?(用比例知识解答)
2.一辆运货汽车从甲地到乙地,平均每小时行驶72千米,10小时到达。回去时空车原路返回,每小时可以比来的时候多行18千米,多长时间能够返回甲地?(用比例解)
3.用18克糖和270克水配制成一杯糖水,如果保持糖水一样甜,加入150克水后需加入多少克糖?
4.开车从安阳到北京要行驶约500千米。一辆汽车从安阳出发前往北京,5小时行了全程的。照这样的速度,到达北京共需要多少小时?
5.在一幅比例尺是的地图上,量得A、B两座城市之间的距离是15cm。一辆客车和一辆小轿车同时从两地相向而行,3小时相遇。已知客车和小轿车的速度比是,这两辆车的速度各是多少?
6.亮亮家造了新房,准备用边长是0.4米的正方形地砖装饰客厅地面,这样需要180块,装修师傅建议改用边长0.6米的正方形地砖铺地。请你算一算需要多少块?(请用比例解答)
7.小林和小华共读一本文学名著,小林每天读20页,6天读完。小华每天读30页,几天可以读完?(用比例解)
(1)分析:每天读的页数和天数成( )比例关系。
(2)请你用比例方法来解答。
8.学校要栽一批树,每班栽20棵,要12个班才能完成任务,如果每班栽30棵,需要几个班可以完成?(用比例解决问题)
9.如图,科学课上,老师在简易杠杆的两边分别放上A、B两个物体。已知A物体重120克,且杠杆保持平衡,那么B物体重多少克?(用比例解答)
10.绍兴地铁1号线全长47.1千米,画在一幅比例尺为1∶150000的地图上,它的图上距离是多少厘米?
11.风能作为一种清洁的可再生能源,越来越受到世界各国的重视。我国风能资源丰富,它取之不尽,用之不竭。某校数学实践小组到石城县八卦脑风景区实践,测得一座风力发电架在阳光下的影长是64米。同时把一根长2米的测杆直立在地上,测得在阳光下的影长是1.6米。风力发电架的高是多少米?(用比例解决问题)
12.给一间长9米,宽6米的教室铺地砖,每块地砖面积与所需地砖的数量如图:
每块地砖的面积/平方厘米 900 1800 3600
所需地砖的数量/块 600 300 150
(1)所需地砖数量与每块地砖的面积成( )比例关系。
(2)如果采用边长50厘米的地砖铺这间教室需要多少块方砖?
13.在比例尺为1∶6000000的地图上,量得A、B两地之间的距离是3厘米,如果一辆汽车以每小时60千米的速度在上午8点从A地出发,问什么时候能到达B地?
14.回答问题。
(1)用数对表示直角三角形ABC的顶点C的位置是(4,2),顶点A的位置是( ),顶点B的位置是( )。
(2)画出三角形ABC向右平移9格后的图形。
(3)画出三角形ABC绕点C顺时针旋转90°后的图形。
(4)画出三角形ABC按2∶1放大后的图形。
15.探索是知识的源泉,请你独立思考后动手操作。
下面每个小方格的边长都表示1厘米。
(1)把图形①绕点B顺时针旋转90°,画出旋转后的图形。旋转后,点C的位置用数对表示为( )。
(2)按1∶2比例画出图形②缩小后的图形。缩小后图形的面积是原来的( )。
(3)在图形③中画出一个最大的圆,这个圆的面积是( )平方厘米。
16.下面是学校附近的平面图。
(1)图书馆在学校正北方向400米处,在图中标出图书馆的位置。
(2)体育馆在学校南偏西40度方向600米处,在图中标出体育馆的位置。
(3)小丽从体育馆向( )偏( )( )度方向走( )米就到学校。
17.化肥厂生产一批化肥,每天生产30吨,50天完成。如果要40天完成任务,每天应多生产多少吨?(用比例解)
18.西安钟楼是中国现存钟楼中形制最大、保存最完整的一座钟楼,总高36米。某展馆设计制作了钟楼的模型,模型的高度与实际高度的比是1∶50。模型的高度是多少米?(用比例解)
19.张同周末去爬山,上山时每小时大约走3.5千米,用了2.4小时,下山时按原路返回,比上山少用了0.3小时,他下山时每小时走多少千米?(用比例解)
20.把1.5米长的竹竿直立在地上,量得它的影长1.2米,同时量得一棵大树的影长3.6米,这棵大树高多少米?(用比例解)
21.下图表示小兔和小羊的奔跑情况。
(1)它们奔跑的路程和所需的时间成( )比例。
(2)根据图象计算小兔18分跑了多少千米?小羊18分跑了多少千米?(用比例解决)
22.在比例尺是1∶2000000的地图上,量的甲乙两地的距离是3.6厘米。如果汽车以每小时30千米的速度于上午8时整从甲地开出,走完这段路程,到达乙地时是什么时间?
参考答案:
1.能
【分析】根据题意可知,汽油的总升数÷行驶的千米数=每千米消耗汽油的升数(一定),则汽油的总升数和行驶的千米数的比值一定,它们成正比例关系,据此设到外婆家需要x升汽油,列比例为x∶460=8∶100,然后解出比例即可。
【详解】解:设到外婆家需要x升汽油。
x∶460=8∶100
100x=8×460
100x=3680
x=3680÷100
x=36.8
36.8<40
40升汽油够用。
答:出发时加满40升汽油,能到外婆家。
【点睛】本题主要考查了正比例的应用,判断相关量是正比例还是反比例是解答本题的关键。
2.8小时
【分析】根据题意可知,汽车的速度×行驶时间=路程(一定),汽车的速度和行驶时间成反比例,据此设x小时能够返回甲地,列比例为(72+18)×x=72×10,然后解出比例即可。
【详解】解:设x小时能够返回甲地。
(72+18)×x=72×10
90x=72×10
90x=720
x=720÷90
x=8
答:8小时能够返回甲地。
【点睛】本题主要考查了反比例的应用,判断相关量是正比例还是反比例是解答本题的关键。
3.10克
【分析】根据题意可知,要保持糖水一样甜,则加入的糖水质量比和原来的质量比一样,据此设加入150克水后需加入x克糖,列比例为150∶x=270∶18,然后解出比例即可。
【详解】解:加入150克水后需加入x克糖。
150∶x=270∶18
270x=150×18
270x=2700
x=2700÷270
x=10
答:加入150克水后需加入10克糖。
【点睛】本题考查了用比例解决问题,掌握解比例的方法是解答本题的关键。
4.6.25小时
【分析】把全长看作单位“1”,根据分数乘法的意义,用500×即可求出5小时行驶的路程,根据路程÷时间=速度,速度一定,路程和时间成正比例,设到达北京共需要x小时,列比例为:500∶x=(500×)∶5,然后解出比例即可。
【详解】解:设到达北京共需要x小时。
500∶x=(500×)∶5
500∶x=400∶5
400x=500×5
400x=2500
x=2500÷400
x=6.25
答:到达北京共需要6.25小时。
【点睛】本题主要考查了正比例的应用,掌握解比例的方法是解答本题的关键。
5.千米/小时;千米/小时
【分析】实际距离=图上距离÷比例尺,依据公式求出实际距离,用实际距离除以时间求出客车和小轿车的速度和,再按比例分配求出他们的速度。
【详解】15÷
=15×3000000
=(厘米)
=450(千米)
(千米/小时)
150÷(2+3)×2
=30×2
=60(千米/小时)
150÷(2+3)×3
=30×3
=90(千米/小时)
答:客车的速度是千米/小时,小轿车的速度是千米/小时。
【点睛】此题考查比例尺的应用,明确实际距离与图上距离的换算方法是解题的关键。
6.80块
【分析】因为每块地砖的面积×地砖的块数=客厅地面的面积(一定),所以每块地砖的面积和地砖的块数成反比例。也就是边长0.4米的地砖的面积×边长0.4米的地砖的块数=边长0.6米的地砖的面积×边长0.6米的地砖的块数,可以根据这个等量关系列比例解答。
【详解】解:设需要x块。
0.6×0.6×x=0.4×0.4×180
0.36x=0.16×180
0.36x=28.8
0.36x÷0.36=28.8÷0.36
x=80
答:需要80块。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
7.(1)反;(2)4天
【分析】(1)根据xy=k(一定),x和y成反比例关系,确定比例关系;
(2)设x天可以读完,根据每天读的页数×读的天数=总页数(一定),列出反比例算式解答即可。
【详解】(1)每天读的页数×读的天数=总页数(一定),每天读的页数和天数成反比例关系。
(2)解:设x天可以读完。
30x=20×6
30x=120
30x÷30=120÷30
x=4
答:4天可以读完。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
8.8个
【分析】由题意可知,这批树的总棵数不变,每班栽树的棵数×需要的班数=这批树的总棵数(一定),则每班栽树的棵数和需要的班数成反比例,据此列出比例并解比例求出未知数的值。
【详解】解:设需要x个班可以完成。
30×x=20×12
30x=240
x=240÷30
x=8
答:需要8个班可以完成。
【点睛】本题主要考查反比例的应用,明确题目中相关联的两种量成反比例关系是解答题目的关键。
9.160克
【分析】根据平衡原理,力臂的长度与所挂重物的质量的乘积一定,所以它们成反比例关系,据此设B物体重x克,列比例为3x=120×4,然后解比例即可。
【详解】解:设B物体重x克。
3x=120×4
3x=480
x=480÷3
x=160
答:B物体重160克。
【点睛】本题考查了反比例的应用,解答本题的关键是理解力臂的长度与所挂重物的质量的乘积是一定的。
10.31.4厘米
【分析】已知比例尺和实际距离,求图上距离,可根据“图上距离=实际距离×比例尺”直接列式计算。
【详解】47.1千米=4710000厘米
4710000×=31.4(厘米)
答:它的图上距离是31.4厘米。
【点睛】图上距离一般用厘米作单位,实际距离一般用米或千米作单位,求图上距离时可先把实际距离换算成以厘米为单位的。
11.80米
【分析】根据实际长与影长的比值不变的关系,列出比例方程进行解答即可。
【详解】解:设风力发电架的高是x米。
答:风力发电架的高是80米。
【点睛】本题考查用比例解决问题,解答本题的关键是掌握题中的数量关系。
12.(1)反;
(2)216块
【分析】(1)判断两种量成正比例还是成反比例,关键看这两种相关联的量中相对应的两个数是比值一定还是乘积一定。如果比值一定,就成正比例;如果乘积一定,就成反比例;如果比值和乘积都不是定量,就不成比例。
(2)每块地砖的面积×所需地砖的块数=这间教室地面的面积(一定),所以所需地砖数量与每块地砖的面积成反比例关系。也就是900×600和边长50厘米的地砖的面积×边长50厘米的地砖的块数相等,可以根据这个数量关系列比例解答。
【详解】(1)900×600=1800×300=3600×150=540000,也就是每块地砖的面积×所需地砖的块数=540000(一定),即每块地砖的面积与所需地砖的块数的乘积一定,所以所需地砖数量与每块地砖的面积成反比例关系。
(2)解:设采用边长50厘米的地砖铺这间教室需要x块方砖,
50×50×x=900×600
2500x=540000
2500x÷2500=540000÷2500
x=216
答:如果采用边长50厘米的地砖铺这间教室需要216块方砖。
【点睛】此题主要考查了反比例的意义及反比例的应用。用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
13.11时
【分析】根据实际距离=图上距离÷比例尺,据此求出A、B两地之间的实际距离,再根据路程÷速度=时间,据此求出汽车行驶的时间,最后用8加上行驶的时间即可求解。
【详解】3÷=3×6000000=18000000(厘米)
18000000厘米=180千米
180÷60=3(小时)
8+3=11(时)
答:11时能到达B地。
【点睛】本题考查路程问题,明确比例尺、图上距离和实际距离之间的关系是解题的关键。
14.(1)(4,5);(2,2)
(2)(3)(4)见详解
【分析】(1)用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
(2)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
(3)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(4)把图形按照n∶1放大,就是将图形的每一条边放大到原来的n倍,放大后图形与原图形对应边长的比是n∶1。
【详解】(1)顶点A的位置是(4,5),顶点B的位置是(2,2)。
(2)(3)(4)
【点睛】关键是掌握用数对表示位置的方法,会作平移和旋转后的图形,图形放大或缩小是指对应边放大或缩小。
15.(1)图见详解;(1,2);(2)图见详解;;(3)图见详解;12.56
【分析】(1)根据图形旋转的特征对图形①进行位置变化。结合数对确定位置的方法:先看在第几列,这个数就是数对中的第一个数,再看在第几行,这个数就是数对中的第二个数,据此确定C点的位置;(2)按1∶2的比例缩小图形②就是将原来图形的长和宽都缩小为原来的,原来的长是4,缩小后的长是2,原来的宽是2,缩小后的宽是1,再根据长方形的面积公式,分别计算出原来长方形的面积和现在长方形的面积,即可解答;(3)要在正方形里面画一个最大的圆,这个圆的直径应该和正方形的边长相等,再根据圆的面积公式,求出圆的面积即可。
【详解】(1)图形①绕点B顺时针旋转90°,B点保持不变,C点旋转到(1,2)处,A点旋转到(3,5)处,见下图:
点C的位置用数对表示为(1,2)。
(2)如下图:
缩小后的长方形面积:1×2=2(平方厘米)
原来的长方形面积:4×2=8(平方厘米)
所以缩小后图形的面积是原来的。
(3)如下图:
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
所以这个圆的面积是12.56平方厘米。
【点睛】本题考查的知识点比较多,解答的关键是熟练掌握作图的特征、数对的写法、长方形的面积公式以及圆的面积公式。
16.(1)、(2)见详解
(3)东;北;50;600
【分析】根据平面图上的方向,上北下南,左西右东,及题中给出的线段比例尺,以学校的位置为观测点,即可标出图书馆及体育馆位置;
以体育馆为观测点,确定学校在体育馆的方向、角度和距离即可确定小丽怎么从体育馆到学校的行走路线。
【详解】(1)400÷200=2(厘米)
(2)600÷200=3(厘米)
图书馆、体育馆位置如下:
(3)以体育馆为观测点,小丽从体育馆向(东)偏(北)(50)度或(北)偏(东)(40)度方向走(600)米就到学校。
【点睛】此题考查了利用方向、角度与距离在平面图中确定物体位置的方法以及线段比例尺的灵活应用。
17.7.5吨
【分析】根据题意知道总工作量一定,工作时间和工作效率成反比例,由此列式解答即可。
【详解】解:设每天应多生产x吨,可得:
40×(30+x)=30×50
1200+40x=1500
1200+40x-1200=1500-1200
40x=300
40x÷40=300÷40
x=7.5
答:每天应多生产7.5吨。
【点睛】解答此题的关键是,弄清题意,根据工作效率、工作时间和工作量之间的关系,先判断哪两种量成何比例,再找准对应量,列式解答即可。
18.0.72米
【分析】根据题意可知,钟楼模型的高度∶钟楼实际的高度=1∶50,据此列出比例方程,并求解。
【详解】解:设模型的高度是米。
∶36=1∶50
50=36×1
=36÷50
=0.72
答:模型的高度是0.72米。
【点睛】本题考查比例的应用,从题目中找到等量关系,根据等量关系列出方程。
19.4千米
【分析】设下山时每小时走x千米。当路程一定时,速度与时间成反比例关系,即上山的速度×上山的时间=下山的速度×下山的时间。根据这个数量关系可有(2.4-0.3)x=3.5×2.4。
【详解】解:设他下山时每小时走x千米。
(2.4-0.3)x=3.5×2.4
2.1x=8.4
x=8.4÷2.1
x=4
答:他下山时每小时走4千米。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
20.4.5米
【分析】竹竿的实际长度和影子长的比,和大树的实际长度和影子长的比是相等的,据此列比例解比例即可。
【详解】解:设这棵大树高x米。
1.5∶1.2=x∶3.6
1.2x=1.5×3.6
1.2x=5.4
1.2x÷1.2=5.4÷1.2
x=4.5
答:这棵大树高4.5米。
【点睛】本题考查了比例的应用,能正确理解题意并列比例是解题的关键。
21.(1)正;(2)21.6千米; 14.4千米
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。根据速度=路程÷时间,观察统计图可知,它们的速度一定,所以它们奔跑的路程和所需的时间成正比例。
(2)设小兔18分跑了x千米,列方程为24∶20=x∶18,然后解出方程即可;设小羊18分跑了y千米,列方程为20∶25=y∶18,然后解出方程即可。
【详解】(1)观察统计图可知,两条线都是直线,所以小兔和小羊的速度一定,则它们奔跑的路程和所需的时间成正比例。
(2)解:设小兔18分跑了x千米。
24∶20=x∶18
20x=24×18
20x=432
x=432÷20
x=21.6
解:设小羊18分跑了y千米。
20∶25=y∶18
25y=20×18
25y=360
y=360÷25
y=14.4
答:小兔18分跑了21.6千米;小羊18分跑了14.4千米。
【点睛】本题考查了正比例的辨识和应用,明确相关联的量是正比例还是反比例是解答本题的关键。
22.10时24分
【分析】根据实际距离=图上距离÷比例尺,据此求出甲乙两地的实际距离,再根据路程÷速度=时间,求出走完这段路需要多长时间,再用8加上走完这段路需要的时间即可求出到达乙地时是什么时间。
【详解】3.6÷=3.6×2000000=7200000(厘米)
7200000厘米=72千米
72÷30=2.4(时)=2时24分
8时+2时24分=10时24分
答:走完这段路程,到达乙地时是10时24分。
【点睛】本题考查路程问题,明确图上距离、实际距离和比例尺之间的关系是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
