必考小专题:比例综合-数学六年级下册苏教版(含解析)
文档属性
| 名称 | 必考小专题:比例综合-数学六年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 518.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 21:00:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
必考小专题:比例综合-数学六年级下册苏教版
1.铺设一条煤气管道。计划每天铺设120米,用12天完成任务。由于居民着急使用,上级要求每天多铺20%,这样可以提前几天完成?(用比例的知识解)
2.明明家的客厅要铺地砖,若用边长为6分米的正方形地砖,需要48块,若用边长为8分米的正方形地砖,则需要多少块呢?(用比例解答)
3.50千克花生能榨18千克花生油,照这样计算,2吨花生能榨多少千克花生油?(用比例解)
4.中国铁路经过第六次提速后,“复兴号”的标准速度为每小时350km,按照这个速度,王叔叔出差选择乘坐“复兴号”,原来7小时的车程现在只需要4小时。原来“复兴号”每小时行驶多少千米?
5.在比例尺是的地图上,量得甲、乙两城之间的距离是7.2厘米。一辆汽车从甲城开到乙城,平均每小时行90千米,需要多长时间?
6.深中通道,又称“深中大桥”,是连接深圳市和中山市以及广州市南沙区的建设中大桥,计划2024年6月建成通车。该桥全程24千米,其中有6.8千米长的沉管隧道。如果一辆汽车通过沉管隧道用时5分钟,按照这个速度,通过全程预计需要多少分钟?(用比例解答,得数保留整数)
7.在一幅比例尺为的地图上,量得甲乙两地之间的公路长8厘米。一辆汽车和一辆货车从两地同时出发相向而行,汽车以每小时65千米的速度行驶,2小时后在超过中点10千米的地方相遇。货车每小时行多少千米?
8.在一幅比例尺是的地图上,量得A、B两地之间的距离是16厘米,一列火车以每小时80千米的速度从地开往地,这列火车行完全程需要多少小时?
9.玩具厂计划生产玩具4800个,前5天生产了300个,照这样计算,玩具厂一共要多少天才能完成任务?(用比例解)
10.赵丽读一本书,如果平均每天读25页,那么8天可以读完;如果赵丽想10天读完,那么平均每天读多少页?(用比例解)
11.六年级学生参加消防知识大赛,参加的男、女生人数之比是。获奖的共110人,其中男、女生人数比为,未获奖的学生中,男、女生人数比是。参加这次消防知识大赛的六年级学生共多少人?
12.乐乐身高1.5米,她的影长是2.1米。如果同时同地测得一棵树的影子长是8.4米,这棵树有多高?(比例解)
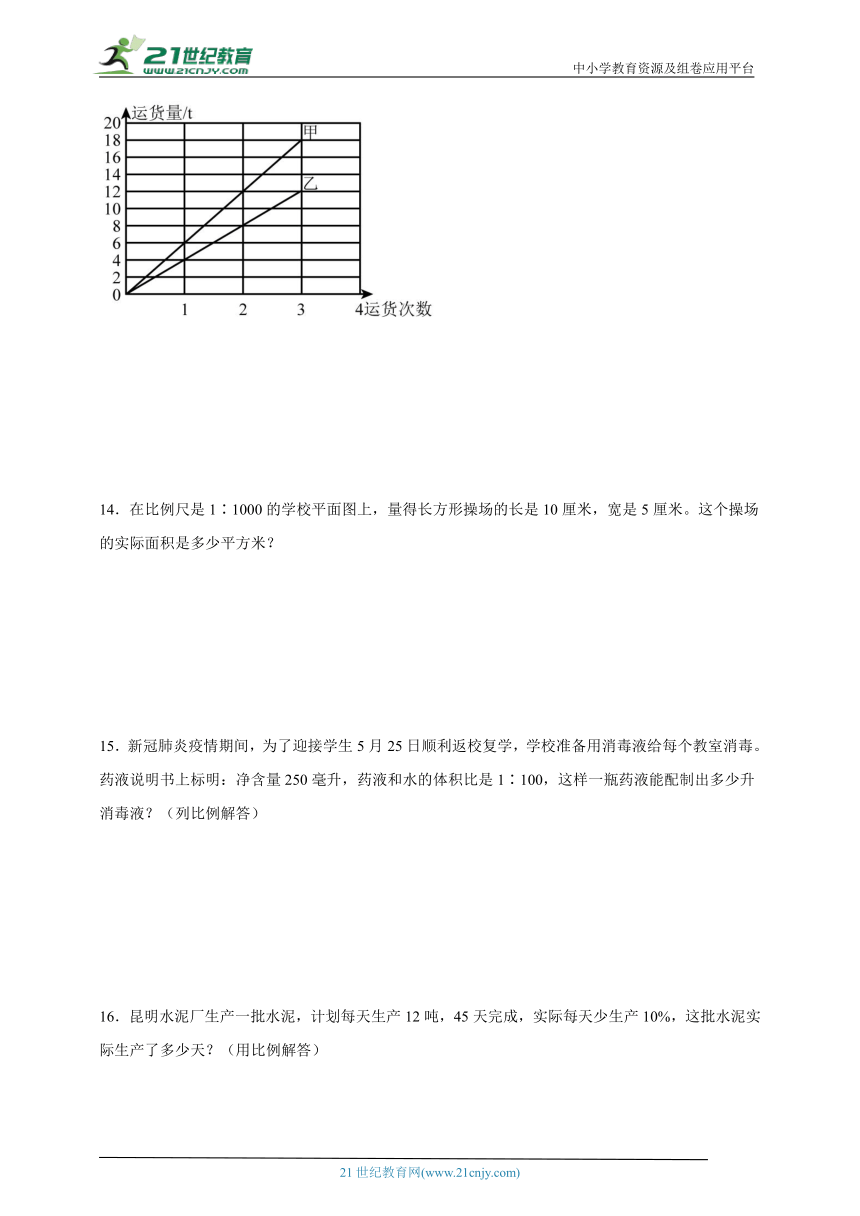
13.如图所示为甲、乙两车的运货量与运货次数的关系图,甲、乙两车各运货6次,运货量相差多少吨?
14.在比例尺是1∶1000的学校平面图上,量得长方形操场的长是10厘米,宽是5厘米。这个操场的实际面积是多少平方米?
15.新冠肺炎疫情期间,为了迎接学生5月25日顺利返校复学,学校准备用消毒液给每个教室消毒。药液说明书上标明:净含量250毫升,药液和水的体积比是1∶100,这样一瓶药液能配制出多少升消毒液?(列比例解答)
16.昆明水泥厂生产一批水泥,计划每天生产12吨,45天完成,实际每天少生产10%,这批水泥实际生产了多少天?(用比例解答)
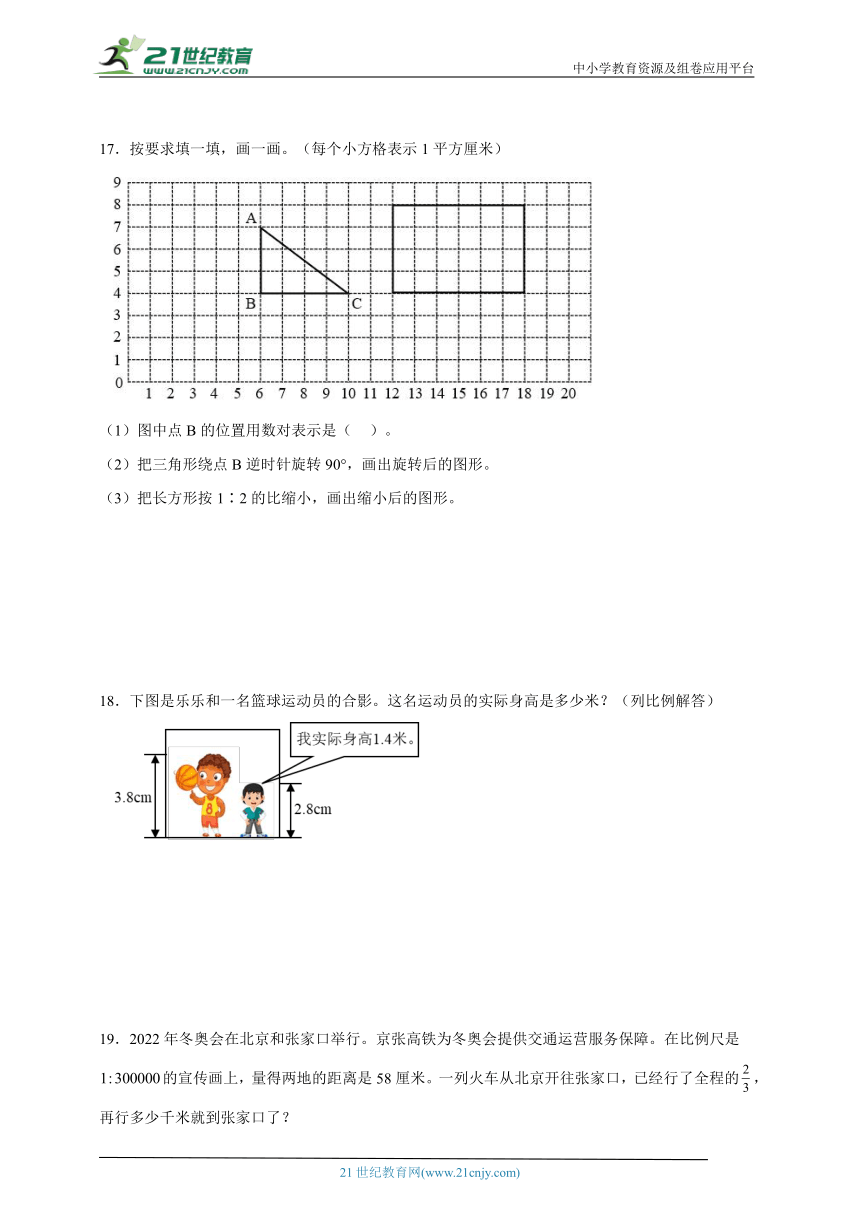
17.按要求填一填,画一画。(每个小方格表示1平方厘米)
(1)图中点B的位置用数对表示是( )。
(2)把三角形绕点B逆时针旋转90°,画出旋转后的图形。
(3)把长方形按1∶2的比缩小,画出缩小后的图形。
18.下图是乐乐和一名篮球运动员的合影。这名运动员的实际身高是多少米?(列比例解答)
19.2022年冬奥会在北京和张家口举行。京张高铁为冬奥会提供交通运营服务保障。在比例尺是的宣传画上,量得两地的距离是58厘米。一列火车从北京开往张家口,已经行了全程的,再行多少千米就到张家口了?
20.花园村新修一条水泥路,每天修的长度和所需天数如下表:
每天修的长度/米 240 80 60 40
所需天数 2 6 8 12
(1)每天修的长度和所需天数成反比例吗?为什么?
(2)如果每天修160米,那么修完这条路需要多少天?
21.某商场开展促销活动,所有商品一律九折优惠。
(1)完成下表。
原价/元 0 10 20 30 40 50
现价/元 0 9
(2)根据表中的数据,在下图中描出原价和现价所对应的点,再按顺序连接起来。
(3)如果用x表示原价,y表示现价,那么y=( )。现价与原价成( )比例。
22.如图。
(1)把图中梯形绕B点按顺时针旋转90°,画出旋转后的图形。旋转后,A点的对应点A′的位置用数对表示是( )。
(2)按1∶2画出直角三角形缩小后的图形。缩小后的三角形面积与原三角形面积的比是( )。
23.下面是森夏买皮球的情况。
数量/个 1 2 3 4 5 6 …
总价/元 6 12 18 24 30 36 …
(1)根据表中的数据,描出各点,再按顺序连接起来。
(2)买8个皮球需要( )元,用108元可以买( )个皮球。
(3)购买皮球的总价和数量成比例吗?如果成比例,成的是什么比例,为什么?
参考答案:
1.2天
【分析】把计划每天铺设的长度(120米)看作单位“1”,则实际每天铺设120×(1+20%)米,设这样可以提前x天完成,实际用了(12-x)天完成。工作效率×工作时间=工作总量(一定),工作效率与工作时间成反比例。即计划每天铺的米数×计划的天数=实际每天铺的米数×实际的天数,据此可列比例“120×12=120×(1+20%)×(12-x)”解答。
【详解】解:设提前x天完成任务。
120×12=120×(1+20%)×(12-x)
1440=120×1.2×(12-x)
1440=144×(12-x)
1440÷144=144×(12-x)÷144
10=12-x
10+x=12-x+x
10+x=12
10+x-10=12-10
x=2
答:这样可以提前2天完成。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
2.27块
【分析】根据题意可知,客厅的面积一定,即一块地砖的面积×地砖的块数=客厅的面积(一定),乘积一定,则一块地砖的面积和地砖的块数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设需要块。
(8×8)=6×6×48
64=1728
64÷64=1728÷64
=27
答:需要27块。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
3.720千克
【分析】由题意可得,花生的出油率是一定的,则榨的花生油的重量与花生的重量成正比例关系,据此即可列比例求解。
【详解】2吨=2000千克
解:设2吨花生能榨x千克花生油,
18∶50=x∶2000
50x=18×2000
50x=36000
x=36000÷50
x=720
答:2吨花生能榨720千克花生油。
【点睛】本题考查了用比例解决问题,注意找出两种相关联的量是成正比例还是反比例。
4.200千米/小时
【分析】根据题意,路程不变,速度提高了,时间减少;用公式:路程=现在的速度×现在的时间,求出总路程,再根据:原来的速度=路程÷原来的时间,据此计算出结果即可。
【详解】350×4÷7
=1400÷7
=200(千米/小时)
答:原来“复兴号”每小时行驶200千米。
【点睛】此题考查了路程问题,可以根据路程一定,速度与时间成反比例关系,再用解比例的知识解答。
5.2小时
【分析】根据“图上距离÷比例尺=实际距离”,先求出甲、乙两城之间的距离,再根据“时间=路程÷速度”,用“甲、乙两城之间的距离”除以速度,即可求出需要的时间。
【详解】7.2÷
=7.2×2500000
=18000000(厘米)
18000000厘米=180千米
180÷90=2(小时)
答:需要2小时。
【点睛】根据图上距离、实际距离和比例尺之间的关系,以及行程问题中的速度、时间和路程之间的关系,是解答此题的关键。
6.18分钟
【分析】速度=路程÷时间,所以速度一定时,路程和时间成正比例关系。据此列方程解答即可。
【详解】解:设按照这个速度,通过全程预计需要x分钟,根据题意列方程:
6.8∶5=24∶x
6.8x=24×5
6.8x=120
x≈18
答:照这个速度,通过全程预计需要18分钟.
【点睛】考查行程问题以及正比例的实际应用,注意保留整数要计算到小数点后第一位,然后根据“四舍五入”法写出答案。
7.55千米
【分析】根据“实际距离=图上距离÷比例尺”求出甲乙两地之间的实际距离,再利用“速度和=总路程÷相遇时间”求出汽车和货车的速度和,最后用减法求出货车速度,据此解答。
【详解】8÷=8×3000000=24000000(厘米)
24000000厘米=240千米
240÷2-65
=120-65
=55(千米)
答:货车每小时行55千米。
【点睛】掌握图上距离和实际距离换算的方法是解答题目的关键。
8.12小时
【分析】先根据“实际距离=图上距离÷比例尺”求出A、B两地间的路程;再根据“路程÷速度=时间”求出这列火车行完全程的时间。
【详解】
=16×6000000
=96000000(厘米)
96000000厘米=960千米
(小时)
答:这列火车行完全程需要12小时。
【点睛】此题考查了图上距离与实际距离的换算、行程问题的数量关系。
9.80天
【分析】300÷5=60(个),即工作效率是每天生产60个。因为,所以工作总量与工作时间成正比例。也就是“300∶5”的比值和“4800∶一共的天数”的比值相等,可以根据这个数量关系列比例解答。
【详解】解:设玩具厂一共要x天才能完成任务。
答:玩具厂一共要80天才能完成任务。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
10.20页
【分析】由题意可知,这本书的页数是一定的,则平均每天读的页数与天数成反比例,据此列比例解答即可。
【详解】解:设平均每天读x页。
10x=25×8
10x=200
10x÷10=200÷10
x=20
答:那么平均每天读20页。
【点睛】本题考查用比例解决实际问题,明确平均每天读的页数与天数成反比例是解题的关键。
11.180人
【分析】根据比的意义,获奖总人数÷总份数,求出一份数,一份数分别乘男、女生的对应份数,求出男生和女生的获奖人数。参加的男、女生人数之比是,设参加这次消防知识大赛的男生有5x人,女生有4x人,根据(男生人数-男生获奖人数)∶(女生人数-女生获奖人数)=4∶3,列出比例求出x的值,再根据5x+4x=六年级参赛人数,列式解答即可。
【详解】110÷(6+5)
=110÷11
=10(人)
10×6=60(人)
10×5=50(人)
解:设参加这次消防知识大赛的男生有5x人,女生有4x人。
(5x-60)∶(4x-50)=4∶3
(4x-50)×4=(5x-60)×3
16x-200=15x-180
16x-200-15x+200=15x-180-15x+200
x=20
20×5+20×4
=100+80
=180(人)
答:参加这次消防知识大赛的六年级学生共180人。
【点睛】关键是理解比的意义,用比例解决问题只要比例两边的比统一即可。
12.6米
【分析】同一时间,同一地点测得物体与影子的比值相等,也就是乐乐的身高与影子的比等于这棵树的高与影子的比,设这棵树的高为x,组成比例,解比例即可。
【详解】解:设这棵树有x米。
1.5∶2.1=x∶8.4
2.1x=1.5×8.4
2.1x=12.6
2.1x÷2.1=12.6÷2.1
x=6
答:这棵树的高是6米。
【点睛】此题考查用比例的知识解应用题,设出未知数,组成比例然后解比例。
13.12吨
【分析】通过观察发现:=…=6(一定),即甲车的运货量与运货次数成正比例,甲车1次运货6吨;=…=4(一定),即乙车的运货量与运货次数成正比例,乙车1次运货4吨。据此先求出甲、乙两车1次运货量的差值,再求出6次运货量的差值。
【详解】(6-4)×6
=2×6
=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨。
【点睛】解决此题关键是读懂甲、乙两车的运货量与运货次数的关系图。正比例关系图象是一条从(0,0)出发的无限延伸的射线。
14.5000平方米
【分析】根据关系式:实际距离=图上距离÷比例尺,即可求得长和宽的实际距离各是多少,再根据长方形的面积=长×宽,即可求解。
【详解】10÷
=10×1000
=10000(厘米)
5÷
=5×1000
=5000(厘米)
10000厘米=100米
5000厘米=50米
100×50=5000(平方米)
答:这个操场的实际面积是5000平方米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
15.25.25升
【分析】已知药液说明书上标明:净含量250毫升,药液和水的体积比是1∶100,由此可知,药液和水的体积成正比例。设这样一瓶药液能需要x升水。据此列比例求出需要水的体积,再加上药液的体积就是消毒液的体积。
【详解】解:设这样一瓶药液需要x升水。
250毫升=0.25升
0.25∶x=1∶100
x=0.25×100
x=25
25+0.25=25.25(升)
答:这样一瓶药液能配制出25.25升消毒液。
【点睛】此题考查的目的是理解掌握正比例的意义及应用。
16.50天
【分析】根据题意,实际每天比计划少生产10%,把计划每天生产水泥的吨数看作单位“1”,则实际每天生产水泥的吨数是计划每天的(1-10%),单位“1”已知,用乘法计算,求出实际每天生产水泥的吨数;
这批水泥的总吨数不变,根据每天生产的吨数×天数=水泥的总吨数(一定),积一定,则每天生产的吨数和天数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设这批水泥实际生产了天。
12×(1-10%)=12×45
12×0.9=540
10.8=540
=540÷10.8
=50
答:这批水泥实际生产了50天。
【点睛】①考查百分数的实际应用,找出单位“1”,单位“1”已知,根据百分数乘法的意义求出实际每天生产水泥的吨数;
②找出相关联的两种量,判断相关联的两种量乘积一定,然后根据反比例的意义列出反比例方程。
17.(1)(6,4)
(2)(3)图形见详解
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出点B的位置。
(2)根据旋转的特征,三角形ABC绕点B逆时针旋转90°,点B的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据图形放大或缩小的意义,把长方形的宽、宽均缩小到原来的所得到的图形就是按1∶2缩小后的图形。
【详解】(1)图中点B的位置用数对表示是(6,4)。
(2)(3)如图所示:
【点睛】本题考查图形的放大或缩小,明确图形放大或缩小后,只是大小变了,形状不变;图形旋转一定度数后,大小、形状不变,只是方向、位置的变化。
18.1.9米
【分析】据题意,乐乐的实际身高是1.4米,在照片中是2.8厘米,那么可设篮球运动员身高是x米,则有“2.8∶1.4 =3.8∶x”这个比例成立,再根据比例的基本性质解这个比例即可得解;据此解答。
【详解】解:设篮球运动员身高是x米,可得:
2.8∶1.4 =3.8∶x
2.8x=1.4×3.8
2.8x=5.32
2.8x÷2.8=5.32÷2.8
x=1.9
答:这名运动员的实际身高是1.9米。
【点睛】利用比例的基本性质进行运算是解答本题的关键。
19.58千米
【分析】根据:图上距离÷比例尺=实际距离,代入数据求得北京、张家口两地的实际距离;因为一列火车行了全程的,再把两地距离看作单位“1”,还要行全程的(1-),根据求一个数的几分之几是多少,用乘法计算,用这个距离乘(1-),即可求出再行多少千米就到张家口了。
【详解】58÷
=58×300000
=17400000(厘米)
17400000厘米=174千米
174×(1-)
=174×
=58(千米)
答:再行58千米就到张家口了。
【点睛】明确图上距离、实际距离的转化方法,且能够熟悉分数乘法的意义,是解题关键。
20.(1)成反比例,每天修的长度×所需天数=480米(一定),乘积一定;
(2)3天
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
(2)根据“工作总量÷工作效率=工作时间”,用480米除以每天修路的长度,即可求出需要的天数。
【详解】(1)240×2=480(米)
80×6=480(米)
60×8=480(米)
40×12=480(米)
每天修的长度×所需天数=480米(一定),乘积一定,所以,每天修的长度和所需天数成反比例。
答:每天修的长度和所需天数成反比例,因为每天修的长度×所需天数=480米(一定),乘积一定。
(2)480÷160=3(天)
答:修完这条路需要3天。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21.(1)18;27;36;45;
(2)见详解;
(3)90%x;正
【分析】(1)根据“所有商品一律九折优惠”可知,现价÷原价=90%,据此分别用原价乘90%,即可求出对应的现价,填表即可。
(2)观察图可知,纵轴表示现价,横轴表示原价,根据表中的数据依次在图中描出各个点并按顺序连接各个点即可。
(3)根据题意可知,现价÷原价=90%,所以,如果用x表示原价,y表示现价,那么y=90%x;现价÷原价=90%(一定),是商(比值)一定,即现价与原价成正比例。
【详解】(1)20×90%
=20×0.9
=18(元)
30×90%
=30×0.9
=27(元)
40×90%
=40×0.9
=36(元)
50×90%
=50×0.9
=45(元)
填表如下:
原价/元 0 10 20 30 40 50
现价/元 0 9 18 27 36 45
(2)作图如下:
(3)根据分析可知,现价÷原价=90%,
如果用x表示原价,y表示现价,那么y=90%x;现价÷原价=90%(一定),是商(比值)一定,即现价与原价成正比例。
【点睛】两种相关联的量,一种量变化, 另一种量也随着变化,如果这两种量相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线。
22.(1)(5,6);图形见详解
(2)1∶4;图形见详解
【分析】①根据旋转的特征,梯形绕B点按顺时针旋转90°后,点B的位置不动,其余各部分均绕点B按相同方向旋转想再的度数,即可画出旋转后的图形A′B′C′D′;根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出点A′的位置。
②图形放大与缩小的意义,把原三角形的各边缩小到原来的,即可画出按1∶2画出直角三角形缩小后的图形;一个图形放大或缩小的倍数是指对应边的放大或缩小的倍数,其面积是这个倍数的平方倍,据此即可写出缩小后的三角形面积与原三角形面积的比,或求出原三形面积和缩小后原三角形面积再比。
【详解】①把图中梯形绕B点按顺时针旋转90°,画出旋转后的图形(下图)。旋转后,A点的对应点A′的位置用数对表示是(5,6)。
②按1∶2画出直角三角形缩小后的图形(下图)。缩小后的三角形面积与原三角形面积的比是(1∶4)。
【点睛】此题是考查作旋转一定度数后的图形、作缩小后的图形、点与数对。作旋转图形要注意旋转方向和旋转角度;图形的放大与缩小是指对应边放大或缩小的倍数,其面积是这个倍数的平方倍;用数对表示点的位置时记住:第一个数字表示列数,第二个数字表示行数。
23.(1)见详解;
(2)48;18;
(3)皮球的总价和数量成比例,成正比例,因为购买皮球总价和数量的比的比值一定。
【分析】(1)观察图可知,纵轴表示总价,横轴表示数量,根据表中的数据依次在图中描出各个点并按顺序连接各个点即可。
(2)根据“总价÷数量=单价”,求出皮球的单价;用皮球的单价乘购买的数量,即可求出买8个皮球需要的钱数;用108元除以皮球的单价,即可求出用108元可以买几个皮球。
(3)根据正反比例的意义可知,相关联的两个变量,比值一定,成正比例;相关联的两个量,乘积一定,成反比例;总价÷数量=单价,又皮球的单价是一定,也就是皮球总价和数量之间的比值一定,据此解题即可。
【详解】(1)作图如下:
(2)6÷1=6(元)
6×8=48(元)
108÷6=18(个)
所以,买8个皮球需要48元,用108元可以买18个皮球。
(3)皮球单价一定,
总价∶数量=单价(一定)
答,皮球的总价和数量成比例,成正比例,因为购买皮球总价和数量的比的比值一定。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
必考小专题:比例综合-数学六年级下册苏教版
1.铺设一条煤气管道。计划每天铺设120米,用12天完成任务。由于居民着急使用,上级要求每天多铺20%,这样可以提前几天完成?(用比例的知识解)
2.明明家的客厅要铺地砖,若用边长为6分米的正方形地砖,需要48块,若用边长为8分米的正方形地砖,则需要多少块呢?(用比例解答)
3.50千克花生能榨18千克花生油,照这样计算,2吨花生能榨多少千克花生油?(用比例解)
4.中国铁路经过第六次提速后,“复兴号”的标准速度为每小时350km,按照这个速度,王叔叔出差选择乘坐“复兴号”,原来7小时的车程现在只需要4小时。原来“复兴号”每小时行驶多少千米?
5.在比例尺是的地图上,量得甲、乙两城之间的距离是7.2厘米。一辆汽车从甲城开到乙城,平均每小时行90千米,需要多长时间?
6.深中通道,又称“深中大桥”,是连接深圳市和中山市以及广州市南沙区的建设中大桥,计划2024年6月建成通车。该桥全程24千米,其中有6.8千米长的沉管隧道。如果一辆汽车通过沉管隧道用时5分钟,按照这个速度,通过全程预计需要多少分钟?(用比例解答,得数保留整数)
7.在一幅比例尺为的地图上,量得甲乙两地之间的公路长8厘米。一辆汽车和一辆货车从两地同时出发相向而行,汽车以每小时65千米的速度行驶,2小时后在超过中点10千米的地方相遇。货车每小时行多少千米?
8.在一幅比例尺是的地图上,量得A、B两地之间的距离是16厘米,一列火车以每小时80千米的速度从地开往地,这列火车行完全程需要多少小时?
9.玩具厂计划生产玩具4800个,前5天生产了300个,照这样计算,玩具厂一共要多少天才能完成任务?(用比例解)
10.赵丽读一本书,如果平均每天读25页,那么8天可以读完;如果赵丽想10天读完,那么平均每天读多少页?(用比例解)
11.六年级学生参加消防知识大赛,参加的男、女生人数之比是。获奖的共110人,其中男、女生人数比为,未获奖的学生中,男、女生人数比是。参加这次消防知识大赛的六年级学生共多少人?
12.乐乐身高1.5米,她的影长是2.1米。如果同时同地测得一棵树的影子长是8.4米,这棵树有多高?(比例解)
13.如图所示为甲、乙两车的运货量与运货次数的关系图,甲、乙两车各运货6次,运货量相差多少吨?
14.在比例尺是1∶1000的学校平面图上,量得长方形操场的长是10厘米,宽是5厘米。这个操场的实际面积是多少平方米?
15.新冠肺炎疫情期间,为了迎接学生5月25日顺利返校复学,学校准备用消毒液给每个教室消毒。药液说明书上标明:净含量250毫升,药液和水的体积比是1∶100,这样一瓶药液能配制出多少升消毒液?(列比例解答)
16.昆明水泥厂生产一批水泥,计划每天生产12吨,45天完成,实际每天少生产10%,这批水泥实际生产了多少天?(用比例解答)
17.按要求填一填,画一画。(每个小方格表示1平方厘米)
(1)图中点B的位置用数对表示是( )。
(2)把三角形绕点B逆时针旋转90°,画出旋转后的图形。
(3)把长方形按1∶2的比缩小,画出缩小后的图形。
18.下图是乐乐和一名篮球运动员的合影。这名运动员的实际身高是多少米?(列比例解答)
19.2022年冬奥会在北京和张家口举行。京张高铁为冬奥会提供交通运营服务保障。在比例尺是的宣传画上,量得两地的距离是58厘米。一列火车从北京开往张家口,已经行了全程的,再行多少千米就到张家口了?
20.花园村新修一条水泥路,每天修的长度和所需天数如下表:
每天修的长度/米 240 80 60 40
所需天数 2 6 8 12
(1)每天修的长度和所需天数成反比例吗?为什么?
(2)如果每天修160米,那么修完这条路需要多少天?
21.某商场开展促销活动,所有商品一律九折优惠。
(1)完成下表。
原价/元 0 10 20 30 40 50
现价/元 0 9
(2)根据表中的数据,在下图中描出原价和现价所对应的点,再按顺序连接起来。
(3)如果用x表示原价,y表示现价,那么y=( )。现价与原价成( )比例。
22.如图。
(1)把图中梯形绕B点按顺时针旋转90°,画出旋转后的图形。旋转后,A点的对应点A′的位置用数对表示是( )。
(2)按1∶2画出直角三角形缩小后的图形。缩小后的三角形面积与原三角形面积的比是( )。
23.下面是森夏买皮球的情况。
数量/个 1 2 3 4 5 6 …
总价/元 6 12 18 24 30 36 …
(1)根据表中的数据,描出各点,再按顺序连接起来。
(2)买8个皮球需要( )元,用108元可以买( )个皮球。
(3)购买皮球的总价和数量成比例吗?如果成比例,成的是什么比例,为什么?
参考答案:
1.2天
【分析】把计划每天铺设的长度(120米)看作单位“1”,则实际每天铺设120×(1+20%)米,设这样可以提前x天完成,实际用了(12-x)天完成。工作效率×工作时间=工作总量(一定),工作效率与工作时间成反比例。即计划每天铺的米数×计划的天数=实际每天铺的米数×实际的天数,据此可列比例“120×12=120×(1+20%)×(12-x)”解答。
【详解】解:设提前x天完成任务。
120×12=120×(1+20%)×(12-x)
1440=120×1.2×(12-x)
1440=144×(12-x)
1440÷144=144×(12-x)÷144
10=12-x
10+x=12-x+x
10+x=12
10+x-10=12-10
x=2
答:这样可以提前2天完成。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
2.27块
【分析】根据题意可知,客厅的面积一定,即一块地砖的面积×地砖的块数=客厅的面积(一定),乘积一定,则一块地砖的面积和地砖的块数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设需要块。
(8×8)=6×6×48
64=1728
64÷64=1728÷64
=27
答:需要27块。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
3.720千克
【分析】由题意可得,花生的出油率是一定的,则榨的花生油的重量与花生的重量成正比例关系,据此即可列比例求解。
【详解】2吨=2000千克
解:设2吨花生能榨x千克花生油,
18∶50=x∶2000
50x=18×2000
50x=36000
x=36000÷50
x=720
答:2吨花生能榨720千克花生油。
【点睛】本题考查了用比例解决问题,注意找出两种相关联的量是成正比例还是反比例。
4.200千米/小时
【分析】根据题意,路程不变,速度提高了,时间减少;用公式:路程=现在的速度×现在的时间,求出总路程,再根据:原来的速度=路程÷原来的时间,据此计算出结果即可。
【详解】350×4÷7
=1400÷7
=200(千米/小时)
答:原来“复兴号”每小时行驶200千米。
【点睛】此题考查了路程问题,可以根据路程一定,速度与时间成反比例关系,再用解比例的知识解答。
5.2小时
【分析】根据“图上距离÷比例尺=实际距离”,先求出甲、乙两城之间的距离,再根据“时间=路程÷速度”,用“甲、乙两城之间的距离”除以速度,即可求出需要的时间。
【详解】7.2÷
=7.2×2500000
=18000000(厘米)
18000000厘米=180千米
180÷90=2(小时)
答:需要2小时。
【点睛】根据图上距离、实际距离和比例尺之间的关系,以及行程问题中的速度、时间和路程之间的关系,是解答此题的关键。
6.18分钟
【分析】速度=路程÷时间,所以速度一定时,路程和时间成正比例关系。据此列方程解答即可。
【详解】解:设按照这个速度,通过全程预计需要x分钟,根据题意列方程:
6.8∶5=24∶x
6.8x=24×5
6.8x=120
x≈18
答:照这个速度,通过全程预计需要18分钟.
【点睛】考查行程问题以及正比例的实际应用,注意保留整数要计算到小数点后第一位,然后根据“四舍五入”法写出答案。
7.55千米
【分析】根据“实际距离=图上距离÷比例尺”求出甲乙两地之间的实际距离,再利用“速度和=总路程÷相遇时间”求出汽车和货车的速度和,最后用减法求出货车速度,据此解答。
【详解】8÷=8×3000000=24000000(厘米)
24000000厘米=240千米
240÷2-65
=120-65
=55(千米)
答:货车每小时行55千米。
【点睛】掌握图上距离和实际距离换算的方法是解答题目的关键。
8.12小时
【分析】先根据“实际距离=图上距离÷比例尺”求出A、B两地间的路程;再根据“路程÷速度=时间”求出这列火车行完全程的时间。
【详解】
=16×6000000
=96000000(厘米)
96000000厘米=960千米
(小时)
答:这列火车行完全程需要12小时。
【点睛】此题考查了图上距离与实际距离的换算、行程问题的数量关系。
9.80天
【分析】300÷5=60(个),即工作效率是每天生产60个。因为,所以工作总量与工作时间成正比例。也就是“300∶5”的比值和“4800∶一共的天数”的比值相等,可以根据这个数量关系列比例解答。
【详解】解:设玩具厂一共要x天才能完成任务。
答:玩具厂一共要80天才能完成任务。
【点睛】用比例知识解决问题关键是找到不变的量,只要两种相关联的量中相对应的两个数的比值一定,就可以用正比例知识解答;只要两种相关联的量中相对应的两个数的乘积一定,就可以用反比例知识解答。
10.20页
【分析】由题意可知,这本书的页数是一定的,则平均每天读的页数与天数成反比例,据此列比例解答即可。
【详解】解:设平均每天读x页。
10x=25×8
10x=200
10x÷10=200÷10
x=20
答:那么平均每天读20页。
【点睛】本题考查用比例解决实际问题,明确平均每天读的页数与天数成反比例是解题的关键。
11.180人
【分析】根据比的意义,获奖总人数÷总份数,求出一份数,一份数分别乘男、女生的对应份数,求出男生和女生的获奖人数。参加的男、女生人数之比是,设参加这次消防知识大赛的男生有5x人,女生有4x人,根据(男生人数-男生获奖人数)∶(女生人数-女生获奖人数)=4∶3,列出比例求出x的值,再根据5x+4x=六年级参赛人数,列式解答即可。
【详解】110÷(6+5)
=110÷11
=10(人)
10×6=60(人)
10×5=50(人)
解:设参加这次消防知识大赛的男生有5x人,女生有4x人。
(5x-60)∶(4x-50)=4∶3
(4x-50)×4=(5x-60)×3
16x-200=15x-180
16x-200-15x+200=15x-180-15x+200
x=20
20×5+20×4
=100+80
=180(人)
答:参加这次消防知识大赛的六年级学生共180人。
【点睛】关键是理解比的意义,用比例解决问题只要比例两边的比统一即可。
12.6米
【分析】同一时间,同一地点测得物体与影子的比值相等,也就是乐乐的身高与影子的比等于这棵树的高与影子的比,设这棵树的高为x,组成比例,解比例即可。
【详解】解:设这棵树有x米。
1.5∶2.1=x∶8.4
2.1x=1.5×8.4
2.1x=12.6
2.1x÷2.1=12.6÷2.1
x=6
答:这棵树的高是6米。
【点睛】此题考查用比例的知识解应用题,设出未知数,组成比例然后解比例。
13.12吨
【分析】通过观察发现:=…=6(一定),即甲车的运货量与运货次数成正比例,甲车1次运货6吨;=…=4(一定),即乙车的运货量与运货次数成正比例,乙车1次运货4吨。据此先求出甲、乙两车1次运货量的差值,再求出6次运货量的差值。
【详解】(6-4)×6
=2×6
=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨。
【点睛】解决此题关键是读懂甲、乙两车的运货量与运货次数的关系图。正比例关系图象是一条从(0,0)出发的无限延伸的射线。
14.5000平方米
【分析】根据关系式:实际距离=图上距离÷比例尺,即可求得长和宽的实际距离各是多少,再根据长方形的面积=长×宽,即可求解。
【详解】10÷
=10×1000
=10000(厘米)
5÷
=5×1000
=5000(厘米)
10000厘米=100米
5000厘米=50米
100×50=5000(平方米)
答:这个操场的实际面积是5000平方米。
【点睛】此题主要考查图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
15.25.25升
【分析】已知药液说明书上标明:净含量250毫升,药液和水的体积比是1∶100,由此可知,药液和水的体积成正比例。设这样一瓶药液能需要x升水。据此列比例求出需要水的体积,再加上药液的体积就是消毒液的体积。
【详解】解:设这样一瓶药液需要x升水。
250毫升=0.25升
0.25∶x=1∶100
x=0.25×100
x=25
25+0.25=25.25(升)
答:这样一瓶药液能配制出25.25升消毒液。
【点睛】此题考查的目的是理解掌握正比例的意义及应用。
16.50天
【分析】根据题意,实际每天比计划少生产10%,把计划每天生产水泥的吨数看作单位“1”,则实际每天生产水泥的吨数是计划每天的(1-10%),单位“1”已知,用乘法计算,求出实际每天生产水泥的吨数;
这批水泥的总吨数不变,根据每天生产的吨数×天数=水泥的总吨数(一定),积一定,则每天生产的吨数和天数成反比例关系,据此列出反比例方程,并求解。
【详解】解:设这批水泥实际生产了天。
12×(1-10%)=12×45
12×0.9=540
10.8=540
=540÷10.8
=50
答:这批水泥实际生产了50天。
【点睛】①考查百分数的实际应用,找出单位“1”,单位“1”已知,根据百分数乘法的意义求出实际每天生产水泥的吨数;
②找出相关联的两种量,判断相关联的两种量乘积一定,然后根据反比例的意义列出反比例方程。
17.(1)(6,4)
(2)(3)图形见详解
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出点B的位置。
(2)根据旋转的特征,三角形ABC绕点B逆时针旋转90°,点B的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据图形放大或缩小的意义,把长方形的宽、宽均缩小到原来的所得到的图形就是按1∶2缩小后的图形。
【详解】(1)图中点B的位置用数对表示是(6,4)。
(2)(3)如图所示:
【点睛】本题考查图形的放大或缩小,明确图形放大或缩小后,只是大小变了,形状不变;图形旋转一定度数后,大小、形状不变,只是方向、位置的变化。
18.1.9米
【分析】据题意,乐乐的实际身高是1.4米,在照片中是2.8厘米,那么可设篮球运动员身高是x米,则有“2.8∶1.4 =3.8∶x”这个比例成立,再根据比例的基本性质解这个比例即可得解;据此解答。
【详解】解:设篮球运动员身高是x米,可得:
2.8∶1.4 =3.8∶x
2.8x=1.4×3.8
2.8x=5.32
2.8x÷2.8=5.32÷2.8
x=1.9
答:这名运动员的实际身高是1.9米。
【点睛】利用比例的基本性质进行运算是解答本题的关键。
19.58千米
【分析】根据:图上距离÷比例尺=实际距离,代入数据求得北京、张家口两地的实际距离;因为一列火车行了全程的,再把两地距离看作单位“1”,还要行全程的(1-),根据求一个数的几分之几是多少,用乘法计算,用这个距离乘(1-),即可求出再行多少千米就到张家口了。
【详解】58÷
=58×300000
=17400000(厘米)
17400000厘米=174千米
174×(1-)
=174×
=58(千米)
答:再行58千米就到张家口了。
【点睛】明确图上距离、实际距离的转化方法,且能够熟悉分数乘法的意义,是解题关键。
20.(1)成反比例,每天修的长度×所需天数=480米(一定),乘积一定;
(2)3天
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
(2)根据“工作总量÷工作效率=工作时间”,用480米除以每天修路的长度,即可求出需要的天数。
【详解】(1)240×2=480(米)
80×6=480(米)
60×8=480(米)
40×12=480(米)
每天修的长度×所需天数=480米(一定),乘积一定,所以,每天修的长度和所需天数成反比例。
答:每天修的长度和所需天数成反比例,因为每天修的长度×所需天数=480米(一定),乘积一定。
(2)480÷160=3(天)
答:修完这条路需要3天。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21.(1)18;27;36;45;
(2)见详解;
(3)90%x;正
【分析】(1)根据“所有商品一律九折优惠”可知,现价÷原价=90%,据此分别用原价乘90%,即可求出对应的现价,填表即可。
(2)观察图可知,纵轴表示现价,横轴表示原价,根据表中的数据依次在图中描出各个点并按顺序连接各个点即可。
(3)根据题意可知,现价÷原价=90%,所以,如果用x表示原价,y表示现价,那么y=90%x;现价÷原价=90%(一定),是商(比值)一定,即现价与原价成正比例。
【详解】(1)20×90%
=20×0.9
=18(元)
30×90%
=30×0.9
=27(元)
40×90%
=40×0.9
=36(元)
50×90%
=50×0.9
=45(元)
填表如下:
原价/元 0 10 20 30 40 50
现价/元 0 9 18 27 36 45
(2)作图如下:
(3)根据分析可知,现价÷原价=90%,
如果用x表示原价,y表示现价,那么y=90%x;现价÷原价=90%(一定),是商(比值)一定,即现价与原价成正比例。
【点睛】两种相关联的量,一种量变化, 另一种量也随着变化,如果这两种量相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,正比例的图像是一条直线。
22.(1)(5,6);图形见详解
(2)1∶4;图形见详解
【分析】①根据旋转的特征,梯形绕B点按顺时针旋转90°后,点B的位置不动,其余各部分均绕点B按相同方向旋转想再的度数,即可画出旋转后的图形A′B′C′D′;根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对表示出点A′的位置。
②图形放大与缩小的意义,把原三角形的各边缩小到原来的,即可画出按1∶2画出直角三角形缩小后的图形;一个图形放大或缩小的倍数是指对应边的放大或缩小的倍数,其面积是这个倍数的平方倍,据此即可写出缩小后的三角形面积与原三角形面积的比,或求出原三形面积和缩小后原三角形面积再比。
【详解】①把图中梯形绕B点按顺时针旋转90°,画出旋转后的图形(下图)。旋转后,A点的对应点A′的位置用数对表示是(5,6)。
②按1∶2画出直角三角形缩小后的图形(下图)。缩小后的三角形面积与原三角形面积的比是(1∶4)。
【点睛】此题是考查作旋转一定度数后的图形、作缩小后的图形、点与数对。作旋转图形要注意旋转方向和旋转角度;图形的放大与缩小是指对应边放大或缩小的倍数,其面积是这个倍数的平方倍;用数对表示点的位置时记住:第一个数字表示列数,第二个数字表示行数。
23.(1)见详解;
(2)48;18;
(3)皮球的总价和数量成比例,成正比例,因为购买皮球总价和数量的比的比值一定。
【分析】(1)观察图可知,纵轴表示总价,横轴表示数量,根据表中的数据依次在图中描出各个点并按顺序连接各个点即可。
(2)根据“总价÷数量=单价”,求出皮球的单价;用皮球的单价乘购买的数量,即可求出买8个皮球需要的钱数;用108元除以皮球的单价,即可求出用108元可以买几个皮球。
(3)根据正反比例的意义可知,相关联的两个变量,比值一定,成正比例;相关联的两个量,乘积一定,成反比例;总价÷数量=单价,又皮球的单价是一定,也就是皮球总价和数量之间的比值一定,据此解题即可。
【详解】(1)作图如下:
(2)6÷1=6(元)
6×8=48(元)
108÷6=18(个)
所以,买8个皮球需要48元,用108元可以买18个皮球。
(3)皮球单价一定,
总价∶数量=单价(一定)
答,皮球的总价和数量成比例,成正比例,因为购买皮球总价和数量的比的比值一定。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
