2023-2024学年数学七年级平面直角坐标系单元测试试题(人教版)基础卷含解析
文档属性
| 名称 | 2023-2024学年数学七年级平面直角坐标系单元测试试题(人教版)基础卷含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 15:03:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级平面直角坐标系(人教版)
单元测试 基础卷 含解析
一、单选题(共30分)
1.(本题3分)如图,枫叶遮盖了一点P,则点P的坐标可能是( )
A. B. C. D.
2.(本题3分)在平面直角坐标系中,点P是y轴上的一点,则点P的坐标可能是( )
A. B. C. D.
3.(本题3分)在平面直角坐标系中,点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(本题3分)已知点在轴上,则点的坐标为( )
A. B. C. D.
5.(本题3分)同学们玩过五子棋吗?它的比赛规则是只要同色5子先成一条直线就算胜.如图,是两人玩的一盘棋,若白①的位置是,黑②的位置是,现轮到黑棋走,甲认为黑棋放在位置就胜利了;乙认为黑棋放在位置就胜利了.你认为( )
A.甲对,乙错 B.甲错,乙对 C.两人都对 D.两人都不对
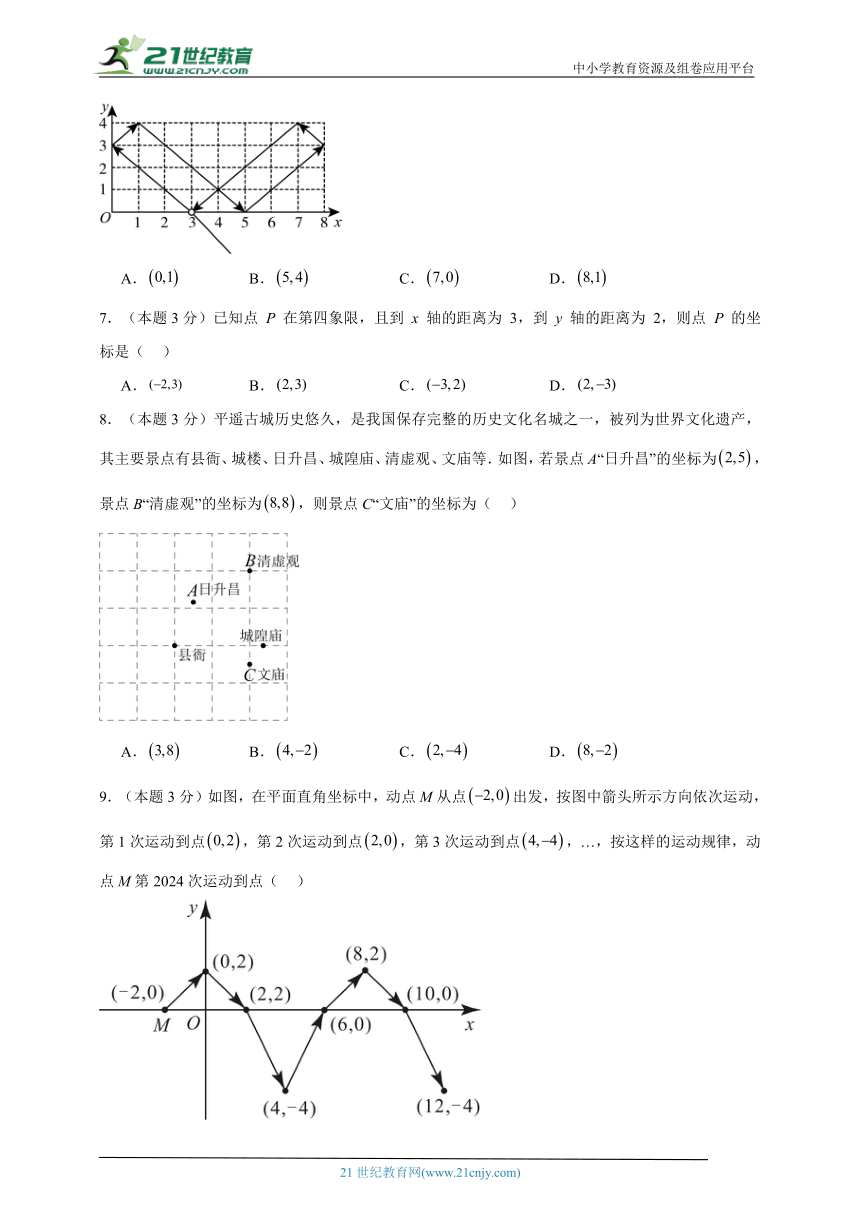
6.(本题3分)如图,小球起始时位于处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是,那么小球第2023次碰到球桌边时,小球的位置是( )
A. B. C. D.
7.(本题3分)已知点 P 在第四象限,且到 x 轴的距离为 3,到 y 轴的距离为 2,则点 P 的坐标是( )
A. B. C. D.
8.(本题3分)平遥古城历史悠久,是我国保存完整的历史文化名城之一,被列为世界文化遗产,其主要景点有县衙、城楼、日升昌、城隍庙、清虚观、文庙等.如图,若景点A“日升昌”的坐标为,景点B“清虚观”的坐标为,则景点C“文庙”的坐标为( )
A. B. C. D.
9.(本题3分)如图,在平面直角坐标中,动点M从点出发,按图中箭头所示方向依次运动,第1次运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,动点M第2024次运动到点( )
A. B. C. D.
10.(本题3分)如图,点,的坐标分别为,.若将线段平移至,点,的坐标分别为,,则的值为( )
A.4 B.3 C.2 D.1
二、填空题(共24分)
11.(本题3分)已知点在第二象限,则点在第 象限.
12.(本题3分)已知点,则点P到y轴的距离为 .
13.(本题3分)如果用表示3排2号,那么3排6号可表示成 .
14.(本题3分)平面直角坐标系中,点向左平移三个单位长度后得到的点的坐标为 .
15.(本题3分)点到两条坐标轴的距离相等,则点的坐标为 .
16.(本题3分)在平面直角坐标系中,轴,,若点,则点的坐标是 .
17.(本题3分)若点A沿x轴正方向平移2个单位所得点的坐标为则点A的坐标为 .
18.(本题3分)在平面直角坐标系中,对于点,我们把叫做点P的友好点.已知点的友好点为,点的友好点为,点的友好点为,这样依次得到各点.若的坐标为,设,则的值为 .
三、解答题(共66分)
19.(本题8分)已知在平面直角坐标系中,点A的坐标为.
(1)若点A在y轴上,求出点A的坐标;
(2)若点A在x轴上方且到x轴的距离为5,求出点A的坐标.
20.(本题8分)适当建立直角坐标系,描出点,,,,,,,,并用线段顺次连接各点,看图案像什么?
21.(本题10分)在平面直角坐标系的位置如图.将向左平移4个单位长度得到,分别为A,B,C的对应点.
(1)画出;
(2)直接写出的坐标.
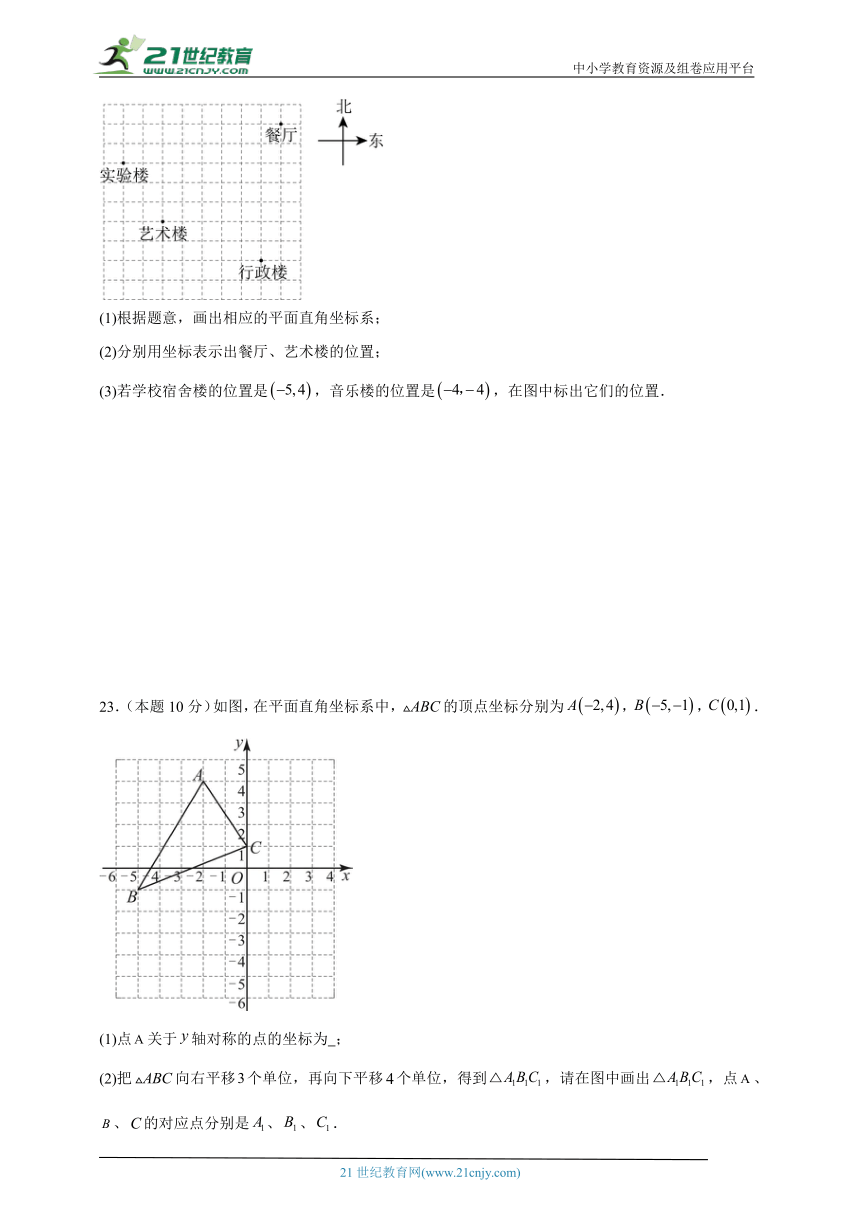
22.(本题10分)如图是小明所在学校的平面示意图,每个小正方形的边长均为1个单位长度,已知实验楼的位置是,行政楼的位置是.
(1)根据题意,画出相应的平面直角坐标系;
(2)分别用坐标表示出餐厅、艺术楼的位置;
(3)若学校宿舍楼的位置是,音乐楼的位置是,在图中标出它们的位置.
23.(本题10分)如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)点关于轴对称的点的坐标为 ;
(2)把向右平移个单位,再向下平移个单位,得到,请在图中画出,点、、的对应点分别是、、.
24.(本题10分)如图是学校的平面示意图,现测得宿舍楼的位置是,艺术楼的位置是.
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出教学楼、体育馆的位置;
(3)若学校行政楼和食堂的位置分别是和,请在图中标出行政楼和食堂的位置.
25.(本题10分)如图1:在平面直角坐标系内,O为坐标原点,线段两端点在坐标轴上且点,点,将向右平移4个单位长度至的位置.
(1)直接写出点C的坐标______;
(2)如图2,过点C作轴于点D,在x轴正半轴有一点,过点E作x轴的垂线,在垂线上有一动点P,求三角形的面积;
(3)如图3,在(2)的条件下,连接,当的面积为时,求点P的坐标.
参考答案:
1.C
【分析】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
根据图形可得点P在第四象限,再根据第四象限内的点的坐标符号为(+,-)进而得出答案.
【详解】解:由图形可得:点的坐标可能是.
故选:C.
2.A
【分析】
本题考查了点的坐标,解题关键是掌握点在y轴上时横坐标为0.根据y轴上的点的特征即可求解.
【详解】解:点P是y轴上的一点,
点P横坐标为0,
故选:A.
3.B
【分析】
本题考查了点的坐标以及象限的特征,根据分别对应的是第一、二、三、四象限进行判断,即可作答.
【详解】解:∵
在平面直角坐标系中,点在第二象限,
故选:B
4.D
【分析】
本题考查了点坐标,解题的关键是正确解出a的值,
直接利用x轴上点的坐标的特征:纵坐标为0,求出a进而可求出答案;
【详解】解:点在轴上,
则:
,
,
,
故选:D
5.C
【分析】
本题主要考查了用坐标系确定位置,根据题意白①的位置是,黑②题意建立坐标系可确定原点的位置,依据题目所给规则进行判定即可得出答案,根据题意建立适当平面直角坐标系坐标系进行求解是解决本题的关键
【详解】解析:根据题意建立平面直角坐标系,如图,由图可知,黑棋放在或位置就胜利了.
故选:C.
6.A
【分析】
本题考查坐标位置,根据题意,可以画出相应的图形,然后即可发现点所在的位置变化特点,即可得到小球第2023次碰到球桌边时,小球的位置.解答本题的关键是明确题意,发现点的坐标位置的变化特点,利用数形结合的思想解答.
【详解】
解:如图,小球第一次碰到球桌边时,小球的位置是
小球第二次碰到球桌边时,小球的位置是
小球第三次碰到球桌边时,小球的位置是
小球第四次碰到球桌边时,小球的位置是
小球第五次碰到球桌边时,小球的位置是
小球第六次碰到球桌边时,小球的位置是
……
∵
∴小球第2023次碰到球桌边时,小球的位置是
故选:A.
7.D
【分析】
本题考查了点的坐标,熟记点到轴的距离等于纵坐标的长度,到轴的距离等于横坐标的长度是解题的关键.根据第四象限内点的横坐标是正数,纵坐标是负数以及点到轴的距离等于纵坐标的长度,到轴的距离等于横坐标的长度解答.
【详解】
解:点在第四象限,且到轴的距离为3,到轴的距离为2,
点的横坐标是2,纵坐标是,
点的坐标是.
故选:D
8.D
【分析】
本题考查建立平面直角坐标系,根据“日升昌”“清虚观”的坐标建立平面直角坐标系,以此即可得到“文庙”的坐标.熟练掌握点的坐标特点是解题的关键.
【详解】解:∵“日升昌”的坐标为,“清虚观”的坐标为,
∴可以建立如图所示的平面直角坐标系,
∴“文庙”的坐标可能是.
故选:D.
9.D
【分析】本题考查点的运动规律,能根据点的运动发现第次为正整数)运动后,动点的坐标是是解题的关键.依次求出前几次运动后点的坐标,再根据坐标的变化规律即可解决问题.
【详解】
解:由题知,
第1次运动后,动点的坐标是;
第2次运动后,动点的坐标是;
第3次运动后,动点的坐标是;
第4次运动后,动点的坐标是;
第5次运动后,动点的坐标是;
第6次运动后,动点的坐标是;
第7次运动后,动点的坐标是;
由此可见,第次为正整数)运动后,动点的坐标是.
又,
即第2024次运动后,动点的坐标是,即.
故选:D
10.B
【分析】
此题主要考查了坐标与图形的变化根据点、平移后横纵坐标的变化可得线段向左平移个单位,向上平移了个单位,然后再确定、的值,进而可得答案.
【详解】
解: 点,的坐标分别为,.点,的坐标分别为,,线段向左平移个单位,向上平移了个单位,
点,的坐标分别为,,
,
故选:B.
11.四
【分析】此题主要考查根据坐标判定点所在的象限,首先根据点A所在的象限可判定,然后即可判定点B所在的象限.
【详解】解:点在第二象限,
,
,
点在第四象限,
故答案为:四.
12.4
【分析】
本题主要考查了点到坐标轴的距离,根据点到x轴的距离为纵坐标的绝对值,点到y轴的距离为横坐标的绝对值进行求解即可.
【详解】解;∵,
∴点P到y轴的距离为,
故答案为:4.
13.
【分析】
本题主要考查了实际问题中用有序数对表示位置,根据题意可知数对的第一个数表示排,第二个数表示号,据此可得答案.
【详解】解:如果用表示3排2号,那么3排6号可表示成,
故答案为:.
14.
【分析】
本题主要考查了坐标与图形变化—平移,根据“左减右加,上加下减”的平移规律求解即可.
【详解】解:∵点向左平移三个单位长度后得到的点,
∴点的坐标为,即,
故答案为;.
15.或
【分析】
本题主要考查点的坐标的意义,绝对值的性质,掌握点的坐标与点到坐标轴的距离的关系是解题的关键.由点到两坐标轴的距离相等,可得到关于a的方程,可求得a的值,则可求得点P的坐标.
【详解】解:点到两条坐标轴的距离相等,
,
或,
解得:或,
当时,,
当时,,
点的坐标为或,
故答案为:或.
16.或
【分析】本题考查了点的坐标特征,根据轴得出点的纵坐标与点的纵坐标相同,为,再由得出点的横坐标即可得解.
【详解】解:轴,
点的纵坐标与点的纵坐标相同,为,
,
点的横坐标为:或,
点的坐标为或,
故答案为:或.
17.
【分析】本题考查坐标与图形变化-平移变换,熟练掌握点的坐标平移规则:左减右加,上加下减是解题的关键.根据平移规则求解即可,
【详解】解:点A沿x轴正方向平移2个单位所得点的坐标为,
故点A的坐标为即,
故答案为:.
18.3
【分析】
本题主要考查了规律型:点的坐标,解答本题的关键是准确理解题意,发现变换规律,求出字母的值.求出、、、的坐标,找到规律,即可求出的值.
【详解】
解:根据题意,点的坐标为,
则,,,,
由此可知,每四次一循环,
因为,
所以与坐标相同,
所以,,
解得:,,
,
,
,
故答案为:3
19.(1)
(2)
【分析】
本题考查了点的坐标,熟练掌握平面直角坐标系中的点的坐标特点是解题的关键.
(1)由y轴上的点的横坐标为0,可得,从而可解得a的值,再将a的值代入计算,则可得答案;
(2)根据点到x轴的距离等于5即为纵坐标的绝对值为5,求解即可.
【详解】(1)
解:∵点A的坐标为,点A在y轴上,
,
,
,
∴点A的坐标为;
(2)
解:∵点A到x轴的距离为5,点A在x轴上方
,
解得,
,
即点A的坐标为.
20.顺次连接各点见解析,像“鱼”
【分析】
本题考查了坐标与图形,解决本题的关键是正确描出各点,描点根据顺序连线即可.
【详解】如图,像“鱼”.
21.(1)作图见详解;
(2)
【分析】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
(1)(2)先利用点的坐标平移规律写出点的坐标,然后描点即可.
【详解】(1)解:由图可知,三个顶点的坐标分别为
向左平移4个单位后,对应顶点的坐标分别为,描出这三个点,连线,如图,为所作;
(2)点的坐标为.
22.(1)见解析
(2)餐厅,艺术楼
(3)见解析
【分析】
此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
(1)根据实验楼和行政楼的坐标,确定原点,再画出平面直角坐标系即可;
(2)根据(1)中建立的平面直角坐标系,即可解答;
(3)根据坐标,再图中标出即可.
【详解】(1)解:如图所示:
(2)解:由图可知:餐厅,艺术楼;
(3)解:宿舍楼和音乐楼的位置如图所示.
23.(1)
(2)图见解析
【分析】
本题考查图形的变换,解题的关键是掌握平移的性质,点在平面直角坐标系的性质,即可.
(1)根据点关于轴对称,纵坐标不变,横坐标互为相反数,即可;
(2)根据平移的性质,即可.
【详解】(1)解:∵的顶点坐标分别为,,
∴点关于轴对称的点的坐标为:
故答案为:.
(2)解:∵的顶点坐标分别为,,,
∴当向右平移个单位,再向下平移个单位时,,;依次连接,,,
∴即为所求.
24.(1)见解析
(2)教学楼的坐标为,体育馆的坐标为
(3)见解析
【分析】
本题主要考查平面直角坐标系:
(1)根据平面直角坐标系的定义,即可找到坐标原点,然后过原点作出轴和轴即可;
(2)过教学楼所在点分别作轴和轴的垂线,垂线与坐标轴的交点所表示的数为相应的横坐标和纵坐标,同理可得体育馆的坐标;
(3)根据行政楼的坐标,分别找出轴和轴上的点,,过这两点分别作所在坐标轴的垂线,两垂线的交点即为所求点,同理可得食堂的位置.
【详解】(1)
(2)教学楼的坐标为,体育馆的坐标为.
(3)行政楼和食堂的位置如图所示.
25.(1)
(2)
(3)或
【分析】本题考查了点的平移,在平面直角坐标系中动点产生三角形的面积;
(1)由点的平移即可求解;
(2)由即可求解;
(3)①当在的上方时,将补成直角梯形,设,由即可求解;②当在轴上方,的下方时,由可判断此情况不存在;③当在的下方时,将补成直角梯形,同理①即可求解;
掌握“割补法”求面积,能根据动点的位置进行分类讨论,并将面积转化为是解题的关键.
【详解】(1)解:由平移得
;
故答案:;
(2)解:如图,
轴,
,
,
∵,轴,
;
故三角形的面积为;
(3)解:①当在的上方时,
如图,将补成直角梯形,
设,
,,,,,
,
的面积为,
,
解得:,
;
②当在轴上方,的下方时,
,
此种情况不存在;
③当在的下方时,
如图,将补成直角梯形,
设,
,,,,,
,
的面积为,
,
解得:,
;
综上所述:点P的坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级平面直角坐标系(人教版)
单元测试 基础卷 含解析
一、单选题(共30分)
1.(本题3分)如图,枫叶遮盖了一点P,则点P的坐标可能是( )
A. B. C. D.
2.(本题3分)在平面直角坐标系中,点P是y轴上的一点,则点P的坐标可能是( )
A. B. C. D.
3.(本题3分)在平面直角坐标系中,点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(本题3分)已知点在轴上,则点的坐标为( )
A. B. C. D.
5.(本题3分)同学们玩过五子棋吗?它的比赛规则是只要同色5子先成一条直线就算胜.如图,是两人玩的一盘棋,若白①的位置是,黑②的位置是,现轮到黑棋走,甲认为黑棋放在位置就胜利了;乙认为黑棋放在位置就胜利了.你认为( )
A.甲对,乙错 B.甲错,乙对 C.两人都对 D.两人都不对
6.(本题3分)如图,小球起始时位于处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是,那么小球第2023次碰到球桌边时,小球的位置是( )
A. B. C. D.
7.(本题3分)已知点 P 在第四象限,且到 x 轴的距离为 3,到 y 轴的距离为 2,则点 P 的坐标是( )
A. B. C. D.
8.(本题3分)平遥古城历史悠久,是我国保存完整的历史文化名城之一,被列为世界文化遗产,其主要景点有县衙、城楼、日升昌、城隍庙、清虚观、文庙等.如图,若景点A“日升昌”的坐标为,景点B“清虚观”的坐标为,则景点C“文庙”的坐标为( )
A. B. C. D.
9.(本题3分)如图,在平面直角坐标中,动点M从点出发,按图中箭头所示方向依次运动,第1次运动到点,第2次运动到点,第3次运动到点,…,按这样的运动规律,动点M第2024次运动到点( )
A. B. C. D.
10.(本题3分)如图,点,的坐标分别为,.若将线段平移至,点,的坐标分别为,,则的值为( )
A.4 B.3 C.2 D.1
二、填空题(共24分)
11.(本题3分)已知点在第二象限,则点在第 象限.
12.(本题3分)已知点,则点P到y轴的距离为 .
13.(本题3分)如果用表示3排2号,那么3排6号可表示成 .
14.(本题3分)平面直角坐标系中,点向左平移三个单位长度后得到的点的坐标为 .
15.(本题3分)点到两条坐标轴的距离相等,则点的坐标为 .
16.(本题3分)在平面直角坐标系中,轴,,若点,则点的坐标是 .
17.(本题3分)若点A沿x轴正方向平移2个单位所得点的坐标为则点A的坐标为 .
18.(本题3分)在平面直角坐标系中,对于点,我们把叫做点P的友好点.已知点的友好点为,点的友好点为,点的友好点为,这样依次得到各点.若的坐标为,设,则的值为 .
三、解答题(共66分)
19.(本题8分)已知在平面直角坐标系中,点A的坐标为.
(1)若点A在y轴上,求出点A的坐标;
(2)若点A在x轴上方且到x轴的距离为5,求出点A的坐标.
20.(本题8分)适当建立直角坐标系,描出点,,,,,,,,并用线段顺次连接各点,看图案像什么?
21.(本题10分)在平面直角坐标系的位置如图.将向左平移4个单位长度得到,分别为A,B,C的对应点.
(1)画出;
(2)直接写出的坐标.
22.(本题10分)如图是小明所在学校的平面示意图,每个小正方形的边长均为1个单位长度,已知实验楼的位置是,行政楼的位置是.
(1)根据题意,画出相应的平面直角坐标系;
(2)分别用坐标表示出餐厅、艺术楼的位置;
(3)若学校宿舍楼的位置是,音乐楼的位置是,在图中标出它们的位置.
23.(本题10分)如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)点关于轴对称的点的坐标为 ;
(2)把向右平移个单位,再向下平移个单位,得到,请在图中画出,点、、的对应点分别是、、.
24.(本题10分)如图是学校的平面示意图,现测得宿舍楼的位置是,艺术楼的位置是.
(1)根据题意,画出相应的平面直角坐标系;
(2)分别写出教学楼、体育馆的位置;
(3)若学校行政楼和食堂的位置分别是和,请在图中标出行政楼和食堂的位置.
25.(本题10分)如图1:在平面直角坐标系内,O为坐标原点,线段两端点在坐标轴上且点,点,将向右平移4个单位长度至的位置.
(1)直接写出点C的坐标______;
(2)如图2,过点C作轴于点D,在x轴正半轴有一点,过点E作x轴的垂线,在垂线上有一动点P,求三角形的面积;
(3)如图3,在(2)的条件下,连接,当的面积为时,求点P的坐标.
参考答案:
1.C
【分析】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
根据图形可得点P在第四象限,再根据第四象限内的点的坐标符号为(+,-)进而得出答案.
【详解】解:由图形可得:点的坐标可能是.
故选:C.
2.A
【分析】
本题考查了点的坐标,解题关键是掌握点在y轴上时横坐标为0.根据y轴上的点的特征即可求解.
【详解】解:点P是y轴上的一点,
点P横坐标为0,
故选:A.
3.B
【分析】
本题考查了点的坐标以及象限的特征,根据分别对应的是第一、二、三、四象限进行判断,即可作答.
【详解】解:∵
在平面直角坐标系中,点在第二象限,
故选:B
4.D
【分析】
本题考查了点坐标,解题的关键是正确解出a的值,
直接利用x轴上点的坐标的特征:纵坐标为0,求出a进而可求出答案;
【详解】解:点在轴上,
则:
,
,
,
故选:D
5.C
【分析】
本题主要考查了用坐标系确定位置,根据题意白①的位置是,黑②题意建立坐标系可确定原点的位置,依据题目所给规则进行判定即可得出答案,根据题意建立适当平面直角坐标系坐标系进行求解是解决本题的关键
【详解】解析:根据题意建立平面直角坐标系,如图,由图可知,黑棋放在或位置就胜利了.
故选:C.
6.A
【分析】
本题考查坐标位置,根据题意,可以画出相应的图形,然后即可发现点所在的位置变化特点,即可得到小球第2023次碰到球桌边时,小球的位置.解答本题的关键是明确题意,发现点的坐标位置的变化特点,利用数形结合的思想解答.
【详解】
解:如图,小球第一次碰到球桌边时,小球的位置是
小球第二次碰到球桌边时,小球的位置是
小球第三次碰到球桌边时,小球的位置是
小球第四次碰到球桌边时,小球的位置是
小球第五次碰到球桌边时,小球的位置是
小球第六次碰到球桌边时,小球的位置是
……
∵
∴小球第2023次碰到球桌边时,小球的位置是
故选:A.
7.D
【分析】
本题考查了点的坐标,熟记点到轴的距离等于纵坐标的长度,到轴的距离等于横坐标的长度是解题的关键.根据第四象限内点的横坐标是正数,纵坐标是负数以及点到轴的距离等于纵坐标的长度,到轴的距离等于横坐标的长度解答.
【详解】
解:点在第四象限,且到轴的距离为3,到轴的距离为2,
点的横坐标是2,纵坐标是,
点的坐标是.
故选:D
8.D
【分析】
本题考查建立平面直角坐标系,根据“日升昌”“清虚观”的坐标建立平面直角坐标系,以此即可得到“文庙”的坐标.熟练掌握点的坐标特点是解题的关键.
【详解】解:∵“日升昌”的坐标为,“清虚观”的坐标为,
∴可以建立如图所示的平面直角坐标系,
∴“文庙”的坐标可能是.
故选:D.
9.D
【分析】本题考查点的运动规律,能根据点的运动发现第次为正整数)运动后,动点的坐标是是解题的关键.依次求出前几次运动后点的坐标,再根据坐标的变化规律即可解决问题.
【详解】
解:由题知,
第1次运动后,动点的坐标是;
第2次运动后,动点的坐标是;
第3次运动后,动点的坐标是;
第4次运动后,动点的坐标是;
第5次运动后,动点的坐标是;
第6次运动后,动点的坐标是;
第7次运动后,动点的坐标是;
由此可见,第次为正整数)运动后,动点的坐标是.
又,
即第2024次运动后,动点的坐标是,即.
故选:D
10.B
【分析】
此题主要考查了坐标与图形的变化根据点、平移后横纵坐标的变化可得线段向左平移个单位,向上平移了个单位,然后再确定、的值,进而可得答案.
【详解】
解: 点,的坐标分别为,.点,的坐标分别为,,线段向左平移个单位,向上平移了个单位,
点,的坐标分别为,,
,
故选:B.
11.四
【分析】此题主要考查根据坐标判定点所在的象限,首先根据点A所在的象限可判定,然后即可判定点B所在的象限.
【详解】解:点在第二象限,
,
,
点在第四象限,
故答案为:四.
12.4
【分析】
本题主要考查了点到坐标轴的距离,根据点到x轴的距离为纵坐标的绝对值,点到y轴的距离为横坐标的绝对值进行求解即可.
【详解】解;∵,
∴点P到y轴的距离为,
故答案为:4.
13.
【分析】
本题主要考查了实际问题中用有序数对表示位置,根据题意可知数对的第一个数表示排,第二个数表示号,据此可得答案.
【详解】解:如果用表示3排2号,那么3排6号可表示成,
故答案为:.
14.
【分析】
本题主要考查了坐标与图形变化—平移,根据“左减右加,上加下减”的平移规律求解即可.
【详解】解:∵点向左平移三个单位长度后得到的点,
∴点的坐标为,即,
故答案为;.
15.或
【分析】
本题主要考查点的坐标的意义,绝对值的性质,掌握点的坐标与点到坐标轴的距离的关系是解题的关键.由点到两坐标轴的距离相等,可得到关于a的方程,可求得a的值,则可求得点P的坐标.
【详解】解:点到两条坐标轴的距离相等,
,
或,
解得:或,
当时,,
当时,,
点的坐标为或,
故答案为:或.
16.或
【分析】本题考查了点的坐标特征,根据轴得出点的纵坐标与点的纵坐标相同,为,再由得出点的横坐标即可得解.
【详解】解:轴,
点的纵坐标与点的纵坐标相同,为,
,
点的横坐标为:或,
点的坐标为或,
故答案为:或.
17.
【分析】本题考查坐标与图形变化-平移变换,熟练掌握点的坐标平移规则:左减右加,上加下减是解题的关键.根据平移规则求解即可,
【详解】解:点A沿x轴正方向平移2个单位所得点的坐标为,
故点A的坐标为即,
故答案为:.
18.3
【分析】
本题主要考查了规律型:点的坐标,解答本题的关键是准确理解题意,发现变换规律,求出字母的值.求出、、、的坐标,找到规律,即可求出的值.
【详解】
解:根据题意,点的坐标为,
则,,,,
由此可知,每四次一循环,
因为,
所以与坐标相同,
所以,,
解得:,,
,
,
,
故答案为:3
19.(1)
(2)
【分析】
本题考查了点的坐标,熟练掌握平面直角坐标系中的点的坐标特点是解题的关键.
(1)由y轴上的点的横坐标为0,可得,从而可解得a的值,再将a的值代入计算,则可得答案;
(2)根据点到x轴的距离等于5即为纵坐标的绝对值为5,求解即可.
【详解】(1)
解:∵点A的坐标为,点A在y轴上,
,
,
,
∴点A的坐标为;
(2)
解:∵点A到x轴的距离为5,点A在x轴上方
,
解得,
,
即点A的坐标为.
20.顺次连接各点见解析,像“鱼”
【分析】
本题考查了坐标与图形,解决本题的关键是正确描出各点,描点根据顺序连线即可.
【详解】如图,像“鱼”.
21.(1)作图见详解;
(2)
【分析】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
(1)(2)先利用点的坐标平移规律写出点的坐标,然后描点即可.
【详解】(1)解:由图可知,三个顶点的坐标分别为
向左平移4个单位后,对应顶点的坐标分别为,描出这三个点,连线,如图,为所作;
(2)点的坐标为.
22.(1)见解析
(2)餐厅,艺术楼
(3)见解析
【分析】
此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.
(1)根据实验楼和行政楼的坐标,确定原点,再画出平面直角坐标系即可;
(2)根据(1)中建立的平面直角坐标系,即可解答;
(3)根据坐标,再图中标出即可.
【详解】(1)解:如图所示:
(2)解:由图可知:餐厅,艺术楼;
(3)解:宿舍楼和音乐楼的位置如图所示.
23.(1)
(2)图见解析
【分析】
本题考查图形的变换,解题的关键是掌握平移的性质,点在平面直角坐标系的性质,即可.
(1)根据点关于轴对称,纵坐标不变,横坐标互为相反数,即可;
(2)根据平移的性质,即可.
【详解】(1)解:∵的顶点坐标分别为,,
∴点关于轴对称的点的坐标为:
故答案为:.
(2)解:∵的顶点坐标分别为,,,
∴当向右平移个单位,再向下平移个单位时,,;依次连接,,,
∴即为所求.
24.(1)见解析
(2)教学楼的坐标为,体育馆的坐标为
(3)见解析
【分析】
本题主要考查平面直角坐标系:
(1)根据平面直角坐标系的定义,即可找到坐标原点,然后过原点作出轴和轴即可;
(2)过教学楼所在点分别作轴和轴的垂线,垂线与坐标轴的交点所表示的数为相应的横坐标和纵坐标,同理可得体育馆的坐标;
(3)根据行政楼的坐标,分别找出轴和轴上的点,,过这两点分别作所在坐标轴的垂线,两垂线的交点即为所求点,同理可得食堂的位置.
【详解】(1)
(2)教学楼的坐标为,体育馆的坐标为.
(3)行政楼和食堂的位置如图所示.
25.(1)
(2)
(3)或
【分析】本题考查了点的平移,在平面直角坐标系中动点产生三角形的面积;
(1)由点的平移即可求解;
(2)由即可求解;
(3)①当在的上方时,将补成直角梯形,设,由即可求解;②当在轴上方,的下方时,由可判断此情况不存在;③当在的下方时,将补成直角梯形,同理①即可求解;
掌握“割补法”求面积,能根据动点的位置进行分类讨论,并将面积转化为是解题的关键.
【详解】(1)解:由平移得
;
故答案:;
(2)解:如图,
轴,
,
,
∵,轴,
;
故三角形的面积为;
(3)解:①当在的上方时,
如图,将补成直角梯形,
设,
,,,,,
,
的面积为,
,
解得:,
;
②当在轴上方,的下方时,
,
此种情况不存在;
③当在的下方时,
如图,将补成直角梯形,
设,
,,,,,
,
的面积为,
,
解得:,
;
综上所述:点P的坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
